提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

卷积

函数f,g是定义在Rn上的可测函数，f与g的卷积记作f*g，它是其中一个函数反转，并平移后，与另一个函数的乘积的积分，是一个对平移量的函数，也就是：

对于定义在整数 Z上的函数f,g，卷积定义为

这里一样把函数定义域以外的值当成零，所以可以扩展函数到所有整数上（如果本来不是的话）。
当g(n)的支撑集（support）为有限长度M，上式会变成有限和：

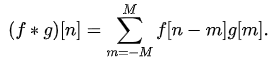
卷积定理指出，函数卷积的傅里叶变换是函数傅里叶变换的乘积。即，一个域中的卷积相当于另一个域中的乘积，例如时域中的卷积就对应于频域中的乘积。

计算卷积的方法：

方法1：直接计算
• 作法：利用卷积的定义

若f[n]和g[n]都为实数信号，则需呀MN个乘法
若f[n]和g[n]都为更一般性的复数信号，不适用复数乘法的快速算法，会需要4MN个乘法；但若使用复数乘法的快速算法，则可以简化至3MN个乘法。因此，使用定义直接计算卷积的复杂度为O(MN)

方法2：快速傅里叶变换（FFT）
• 概念：由于两个离散信号在时域（time domain）做卷积相当于这两个信号的离散傅里叶变换在频域（frequency domain）做相乘：

可以看出在频域的计算较简单。

• 作法：因此这个方法即是先将信号从时域转成频域：

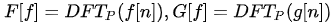
，于是

最后再将频域信号转回时域，就完成了卷积的计算，总共做了2次DFT和1次IDFT。

自相关

在信号处理中，上面的定义通常不进行归一化，即不减去均值并除以方差。当自相关函数由均值和方差归一化时，有时会被称作自相关系数
给定一个信号 f(t)，连续的自相关函数通常定义为f(t)与其自身延迟的连续互相关。

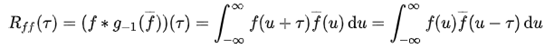
互相关

在信号处理领域中，互相关（有时也称为“互协方差”）是用来表示两个信号之间相似性的一个度量，通常通过与已知信号比较用于寻找未知信号中的特性。它是两个信号之间相对于时间的一个函数，有时也称为“滑动点积”

• 互相关与卷积通过下式发生关系：

• 由卷积定理可推得：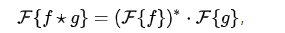

卷积、自相关、互相关的可视化比较

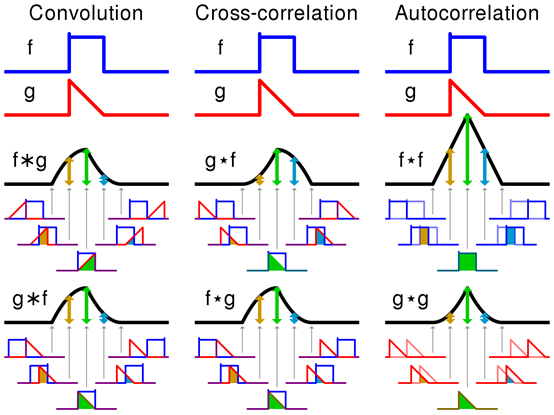
应用实例

卷积
滤波器如FIR滤波器。实际就是输入信号与系数进行卷积运算。而且根据卷积定理，时域的卷积等于频域的相差。而我们对系数进行傅里叶变化则得到了滤波器的幅频响应

相关

相关运算很多情况下用于时域位置的寻找。
移动通信中LTE信号PSS信号的查找就是复数自相关与互相关
GPS信号中的伪码捕获就是C/A码的实数自相关与互相关

GPS 1号星的C/A码PRN1的自相关特性

GPS 1号星的C/A码PRN1和GPS 1号星的C/A码PRN2的互相关特性