一、理论基础

1、GWO算法

请参考这里。

2、TGWO算法

2.1 Tent混沌映射

混沌具有随机性和遍历性和初值敏感性，能使算法有更快的收敛速度。本文采用Tent映射来产生混沌序列，对种群进行初始化，使得初始解尽可能均匀的分布在解空间内。基于Tent映射生成混沌序列$Z_I^k$过程如下： Z I + 1 k = { Z I k u ,      0 ≤ Z I k ≤ u 1 − Z I k 1 − u , u < Z I k ≤ 1 (1) Z_{I+1}^k=\begin{dcases}\frac{Z_I^k}{u},\quad\quad\,\,\,\,0≤Z_I^k≤u\\[2ex]\frac{1-Z_I^k}{1-u},\quad u<Z_I^k≤1\end{dcases}

\tag{1} ZI+1k​=⎩⎪⎪⎨⎪⎪⎧​uZIk​​,0≤ZIk​≤u1−u1−ZIk​​,u<ZIk​≤1​(1)其中，$k$为种群数，$I$为当前迭代次数，为保持算法初始化信息的随机性，$u$取值为$u\subset rand(0,1)$。
结合混沌序列$Z_I^k$，进一步生成搜索区域内的灰狼个体初始位置序列$X_I^k$过程如下：$$X_I^k=X_{I,\min }^k+Z_I^k\left(X_{I,\max }^k-X_{I,\min }^k\right)\text{\hspace{1em}(2)}$$其中，$X_{I,\max }^k$、$X_{I,\min }^k$分别为$X_I^k$序列的最大值与最小值。

2.2 控制参数调整

2.2.1 指数型收敛因子$a$策略

GWO算法的实际寻优过程中，搜寻范围需要非线性动态调整，线型收敛因子$a$所决定搜索半径$\mathbf{V}$的变化不能客观、完整体现实际搜索过程。为此，本文提出一种指数型的收敛因子$a$更新策略，更好地拟合GWO算法中收敛因子$a$实际非线性变化过程。更新公式如下：$$a(I)=a_s+(a_s-a_e)\times {\left[{\left(1-\frac{I}{MaxIter}\right)}^{{\lambda }_1}\right]}^{{\lambda }_2}\text{\hspace{1em}(3)}$$其中，$a_s=2$、$a_e=0$分别表示收敛因子起始、终止值；${\lambda }_1,{\lambda }_2\in (0,1)$分别为非线性调节系数。

2.2.2 控制参数$\mathbf{H}$调整策略

在GWO算法中，参数$\mathbf{H}$同样决定着灰狼与猎物的靠近程度，为进一步地平衡算法的全局与局部搜索提出如下改进策略：$$\mathbf{H}=2\times {\mathbf{r}}_3-a\text{\hspace{1em}(4)}$$其中，$a$由式(3)所得； ${\mathbf{r}}_3$为$[1,1.5]$内随机向量。
由式(4)可得，控制参数$\mathbf{H}$的调整策略中引入改进过后的指数型收敛因子$a$，在拟合狼群实际搜索过程的基础上，进一步调节参数$\mathbf{H}$。在搜索前期，满足$|\mathbf{H}|<1$，提升狼群全局勘探能力，丰富狼群位置分布的多样性；在搜索后期，满足$|\mathbf{H}|>1$，增强GWO算法局部开采能力，准确锁定全域最优值，提高收敛速度。随机向量${\mathbf{r}}_3$的引入同样增加狼群搜索位置的遍历性。

2.3 改进位置更新公式

2.3.1 动态权重因子

受PSO惯性权重启发，引入动态权重因子$b$，动态更新灰狼个体步长。$$b(I)=b_f-\frac{I}{MaxIter}(b_f-b_s)\text{\hspace{1em}(5)}$$其中，$b_s$、$b_f$分别表示权重因子的初值和终值。

2.3.2 适应度比例系数

为有效区分头狼$\alpha$、$\beta$、$\delta$的不同引导作用，在原始静态平均的基础上，引入适应度比例系数，动态加权平均以区分头狼贡献率，引导后续灰狼个体位置更新。适应度比例系数计算如下： { f = ∣ f α + f β + f δ ∣ v 1 = f α f ,    v 2 = f β f ,    v 3 = f δ f f > 0 v 1 = v 2 = v 3 = 1 3    f = 0 (6) \begin{dcases}f=\left|f_\alpha+f_\beta+f_\delta\right|\\[2ex]v_1=\frac{f_\alpha}{f},\,\,v_2=\frac{f_\beta}{f},\,\,v_3=\frac{f_\delta}{f}\quad f>0\\[2ex]v_1=v_2=v_3=\frac13\quad\quad\quad\quad\quad\,\, f=0\end{dcases}

\tag{6} ⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧​f=∣fα​+fβ​+fδ​∣v1​=ffα​​,v2​=ffβ​​,v3​=ffδ​​f>0v1​=v2​=v3​=31​f=0​(6)其中，$v_1$、$v_2$、$v_3$为适应度比例系数；$f_{\alpha }$、$f_{\beta }$、$f_{\delta }$分别为$\alpha$、$\beta$、$\delta$的适应度值。

2.3.3 融合改进的位置更新公式

$$\mathbf{X}(I+1)=b(I)\cdot {\mathbf{r}}_4\cdot (v_1\cdot {\mathbf{X}}_1+v_2\cdot {\mathbf{X}}_2+v_3\cdot {\mathbf{X}}_3)\text{\hspace{1em}(7)}$$其中，${\mathbf{r}}_4$为$[0,1]$间的随机向量；$b(I)$由式(5)计算所得；$v_1$、$v_2$、$v_3$由式(6)计算所得。
在新的位置更新公式(7)中，首先，引入呈线型递减变化的动态权重因子，综合考虑狼群捕猎实际过程中，猎物位置移动的多变性以及灰狼个体位置更新的自主性，动态调整步长更新，更好地开发GWO算法的搜索寻优能力；其次，引入适应度比例系数，根据适应度值不同，权衡$\alpha$、$\beta$、$\delta$头狼对后续灰狼个体位置更新的不同引导作用，更有利于后续的底层灰狼个体趋近于全局最优解来更新位置；有效地拟合灰狼个体实际位置更新过程，提升算法在全域搜索的遍历性，以防止陷入局部范围的早熟停滞。

2.4 TGWO算法流程

Step1: 输入种群规模$N$，搜索维度$dim$，非线性调节系数${\lambda }_1,{\lambda }_2$，最大迭代次数$MaxIter$；
Step2: 初始化灰狼个体$\alpha$、$\beta$、$\delta$的适应度值$f({\mathbf{X}}_{\alpha })$、$f({\mathbf{X}}_{\beta })$、$f({\mathbf{X}}_{\delta })$；位置空间${\mathbf{X}}_{\alpha }$、${\mathbf{X}}_{\beta }$、${\mathbf{X}}_{\delta }$；
Step3: 基于Tent混沌映射形成初始种群 { X i } \{\boldsymbol X_i\} {Xi​}，其中$i=1,2,\cdots ,N$；
Step4: 计算灰狼个体适应度值$f({\mathbf{X}}_i)$，并进行排序，其中$i=1,2,\cdots ,N$；
Step5: 将适应度值排名位于第一、第二、第三的灰狼个体记为$\alpha$、$\beta$、$\delta$，并记录其位置信息${\mathbf{X}}_{\alpha }$、${\mathbf{X}}_{\beta }$、${\mathbf{X}}_{\delta }$；
Step6: 分别根据式(3)更新收敛因子$a$，相应得出搜索半径$\mathbf{V}$的值，根据式(4)更新$\mathbf{H}$的值，根据式(5)更新动态权重因子$b$的值；
Step7: 依据2.3节所述对位置更新公式的融合改进策略，先后根据式(5)、(6)、(7)更新狼群个体位置；
Step8: 如果$I<MaxIter$，则令$I=I+1$，返回Step4，否则算法迭代结束，将最优适应度值及最佳位置输出。

二、仿真实验与结果分析

将TGWO与GWO和WOA进行对比，以文献[1]中表2的8个测试函数为例，实验设置种群规模为30，最大迭代次数为500，每种算法独立运算30次，结果显示如下：

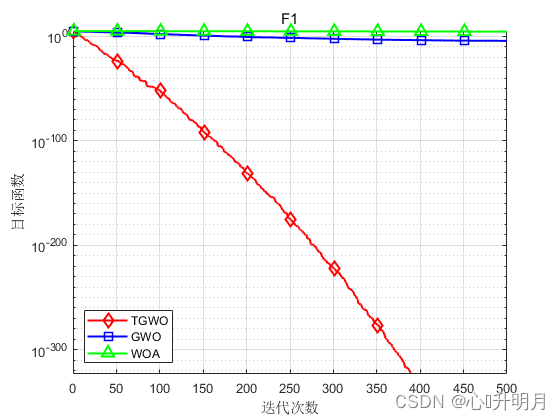
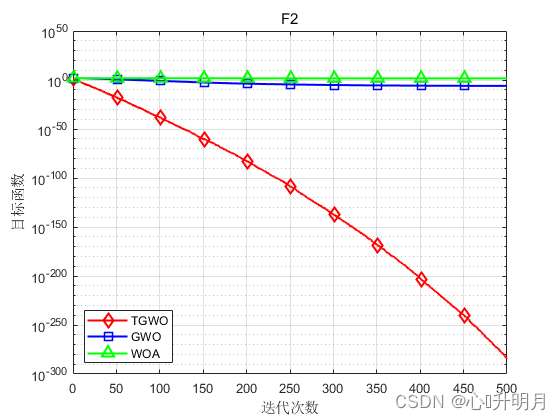
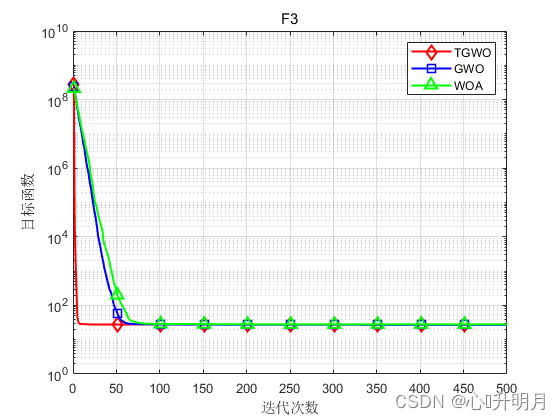
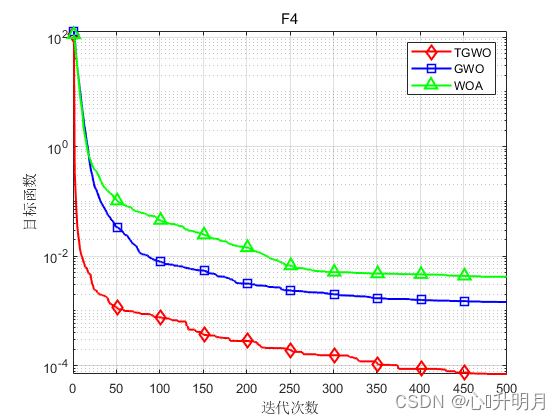
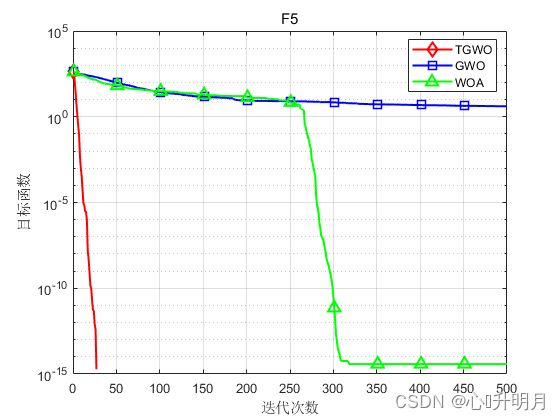
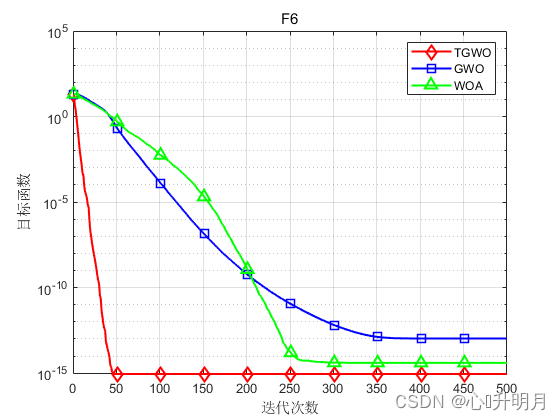
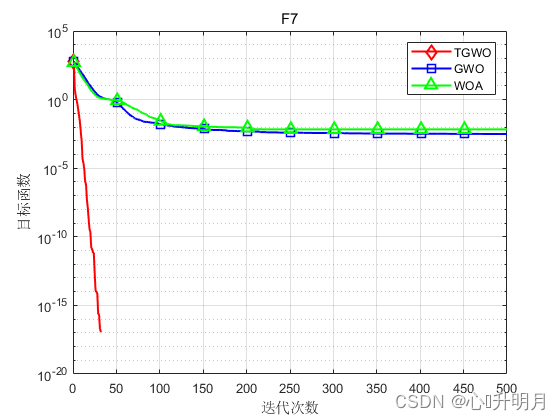
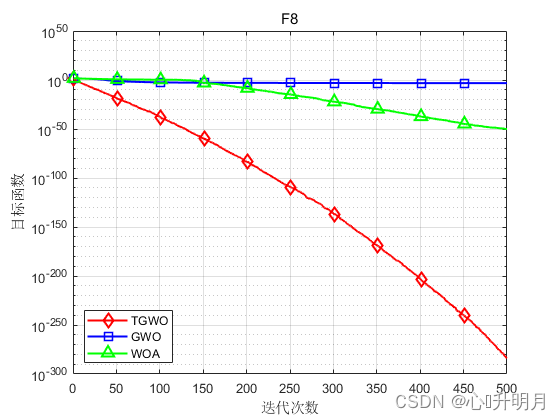
函数：F1
TGWO：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
GWO：最差值: 0.0016743, 最优值: 9.5831e-09, 平均值: 6.2089e-05, 标准差: 0.00030547, 秩和检验: 1.2118e-12
WOA：最差值: 65354.1291, 最优值: 19454.0585, 平均值: 43745.0368, 标准差: 13520.6414, 秩和检验: 1.2118e-12
函数：F2
TGWO：最差值: 6.8913e-284, 最优值: 2.7582e-293, 平均值: 3.0196e-285, 标准差: 0, 秩和检验: 1
GWO：最差值: 2.8709e-06, 最优值: 1.5594e-07, 平均值: 9.5599e-07, 标准差: 8.4683e-07, 秩和检验: 3.0199e-11
WOA：最差值: 91.2283, 最优值: 2.8521, 平均值: 47.1139, 标准差: 29.1653, 秩和检验: 3.0199e-11
函数：F3
TGWO：最差值: 28.7545, 最优值: 1.014, 平均值: 27.8004, 标准差: 5.0592, 秩和检验: 1
GWO：最差值: 28.7174, 最优值: 25.9235, 平均值: 27.0304, 标准差: 0.8222, 秩和检验: 1.287e-09
WOA：最差值: 28.775, 最优值: 27.1884, 平均值: 27.967, 标准差: 0.44562, 秩和检验: 9.0632e-08
函数：F4
TGWO：最差值: 0.00023008, 最优值: 2.2637e-07, 平均值: 7.059e-05, 标准差: 5.4762e-05, 秩和检验: 1
GWO：最差值: 0.0033817, 最优值: 0.00034255, 平均值: 0.0014612, 标准差: 0.00077182, 秩和检验: 3.0199e-11
WOA：最差值: 0.018087, 最优值: 6.6458e-05, 平均值: 0.0042044, 标准差: 0.0049256, 秩和检验: 1.4643e-10
函数：F5
TGWO：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
GWO：最差值: 24.5669, 最优值: 5.6843e-14, 平均值: 4.076, 标准差: 5.1695, 秩和检验: 1.197e-12
WOA：最差值: 1.1369e-13, 最优值: 0, 平均值: 3.7896e-15, 标准差: 2.0756e-14, 秩和检验: 0.33371
函数：F6
TGWO：最差值: 8.8818e-16, 最优值: 8.8818e-16, 平均值: 8.8818e-16, 标准差: 0, 秩和检验: NaN
GWO：最差值: 1.3589e-13, 最优值: 6.4837e-14, 平均值: 1.0522e-13, 标准差: 1.6806e-14, 秩和检验: 1.1303e-12
WOA：最差值: 7.9936e-15, 最优值: 8.8818e-16, 平均值: 3.9672e-15, 标准差: 2.234e-15, 秩和检验: 9.1593e-09
函数：F7
TGWO：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
GWO：最差值: 0.023842, 最优值: 0, 平均值: 0.0030976, 标准差: 0.0066579, 秩和检验: 0.0055843
WOA：最差值: 0.20178, 最优值: 0, 平均值: 0.0067259, 标准差: 0.036839, 秩和检验: 0.33371
函数：F8
TGWO：最差值: 5.0698e-283, 最优值: 7.3324e-295, 平均值: 1.7692e-284, 标准差: 0, 秩和检验: 1
GWO：最差值: 0.0024596, 最优值: 1.2696e-16, 平均值: 0.00062083, 标准差: 0.00066305, 秩和检验: 3.0199e-11
WOA：最差值: 1.1809e-49, 最优值: 4.2689e-59, 平均值: 8.2504e-51, 标准差: 2.6665e-50, 秩和检验: 3.0199e-11
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

实验结果表明：TGWO算法在单峰、多峰函数上均有较好的收敛性、较高的寻优精度。

三、参考文献

[1] 刘志强, 何丽, 袁亮, 等. 采用改进灰狼算法的移动机器人路径规划[J/OL]. 西安交通大学学报, 2022(10): 1-11 [2022-06-24].