-
高数 | 精通中值定理 解题套路汇总
解题套路汇总
套路一









注:柯西中值定理中的 g‘(x)≠0 同时限制了两个分母 可以用反证法+罗尔
注:一个点处的导数正负无法判断函数的单调性,但至少可以判断出这个点的去心邻域的函数值与该点本 身的函数值的大小关系。具体来说即为脱帽法。- 1、若
 ,则
,则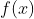 在
在 的右去心邻域的函数值比
的右去心邻域的函数值比 大,去心左邻域的函数值比
大,去心左邻域的函数值比 小,可简记为“
小,可简记为“ 左低右高”。
左低右高”。 - 2、若
 有类似的结论,可简记为“
有类似的结论,可简记为“ 左高右低”.
左高右低”.

 利用脱帽法结论,我们可以轻松证明费马定理。类题:请叙述并证明费马定理、导数零点定理、导数介值定理 ( 也叫达布定理 ) .
利用脱帽法结论,我们可以轻松证明费马定理。类题:请叙述并证明费马定理、导数零点定理、导数介值定理 ( 也叫达布定理 ) .














罗尔定理得到的根一定是单根。

套路二 辅助多项式

【注】构造
 的目的,主要是将题干中的那些“参差不齐”的函数值和导数值全部“归零”,从而使得
的目的,主要是将题干中的那些“参差不齐”的函数值和导数值全部“归零”,从而使得 能够不断使用罗尔定理,大大简化了问题!
能够不断使用罗尔定理,大大简化了问题!
【注】设函数时,若已知零点,举例,比如二次函数:设为





【注】回顾辅助多项式的解题过程可知,由于
 是n次多项式,而我们最后还是对辅助函数
是n次多项式,而我们最后还是对辅助函数 连续求了n次导,从而得到了
连续求了n次导,从而得到了 ,所以真正影响、决定最终结论的,只有
,所以真正影响、决定最终结论的,只有 中的最高次项的系数!而至于那些低次项都在一次次的求导过程中消失殆尽了。
中的最高次项的系数!而至于那些低次项都在一次次的求导过程中消失殆尽了。(当然,这不代表那些低次项的系数可以随便乱写,因为只有
 中的每一个系数都准确无误时,
中的每一个系数都准确无误时, 才可能出现那么多的零点和驻点,才可能满足罗尔定理的使用条件,你不能因为那些低次项的系数不影响
才可能出现那么多的零点和驻点,才可能满足罗尔定理的使用条件,你不能因为那些低次项的系数不影响 ,你就认为他们毫无作用,工具人也是人~)
,你就认为他们毫无作用,工具人也是人~)




【注】特别注意的是,本题中
 和
和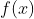 虽然有相同的最小值
虽然有相同的最小值 ,但它们取到最小值的横坐标却不一定相同。故需要分类讨论。该思想可以应用到2007年的考研大题中!
,但它们取到最小值的横坐标却不一定相同。故需要分类讨论。该思想可以应用到2007年的考研大题中!

【注】
前文中已经提过,在使用辅助多项式解题时,若预证结论为
 ,则需要构造一个
,则需要构造一个 次多项式进行拟合。由于n次多项式中有
次多项式进行拟合。由于n次多项式中有 个系数,所以题干中只有
个系数,所以题干中只有 个独立条件时,则无法顺利解出辅助函数中所有系数。
个独立条件时,则无法顺利解出辅助函数中所有系数。为了解决这个问题,我们需要给
 “强行附加约束条件”,使得构造出的
“强行附加约束条件”,使得构造出的
能够顺利解出题目。
至于需要附加一个什么样的条件,则需要“具体问题具体分析”,不能一概而论,但核心原则是“缺什么补什么”。




补充例题:

【解答】
见到题目给出三个点我们很容易想到罗尔定理

却发现这三个点不相等,那么我们会立马想到泰勒定理

但在考研数学中不能直接使用导数介值定理(这里注意本题的题干[没给连续]),所以我们可以想到什么来规避它呢?
构造辅助多项式:


【真题】


套路三 公式法(积分因子法)

【注意】
1、公式中的
 不需要加任意常数
不需要加任意常数 ,因为我们只需要找到一个辅助函数就够了。
,因为我们只需要找到一个辅助函数就够了。2、
 不一定恰好就是欲证结论,有时需要再变形一下才行,但一定要注意——对
不一定恰好就是欲证结论,有时需要再变形一下才行,但一定要注意——对 变形时,如果等式两边同时约去某个东西,或者同除某个东西,需要考虑它是否为0.
变形时,如果等式两边同时约去某个东西,或者同除某个东西,需要考虑它是否为0.



需要分类讨论:
①如果ξ≠0,则在F'(ξ)=0两边约去ξ,得到欲证结论;
②如果ξ=0,那说明0在区间(a,b)内部,即在定义域内部。
又因为F(x)=x²f(x),所以F(0)=0,而又因为F(a)=F(b)=0,所以推出F有三个零点,分别是a,0,b。
所以我们在【a,0】和【0,b】分别用罗尔定理,即可证出存在两个不为0的ξ1和ξ2,
使得F'(ξ1)=F'(ξ2)=0,此时由于ξ1和ξ2不为0,所以是可以被约去。









【注1】本题欲证结论为
 ,最直观的感觉就是“一阶导
,最直观的感觉就是“一阶导 哪去了?”。所以,这种题目一般都需要认为引入一阶导
哪去了?”。所以,这种题目一般都需要认为引入一阶导 ,达到一个降阶的效果。
,达到一个降阶的效果。【注2】本题在欲证等式两边同时减去
 ,其实也可以,本质是一样的。
,其实也可以,本质是一样的。【注3】若欲证结论中已经含有
 ,则不需要再人为引入
,则不需要再人为引入 了,但有时需要将一阶导
了,但有时需要将一阶导 合理分配,使他们达到一种“平衡”。
合理分配,使他们达到一种“平衡”。合理分配,达到平衡

 【注】将用这道题为例给大家展示为什么在马克总主义哲学中,会强调“真理与语误可以相互转化”,也隐藏着以后会显露出来的真理的成分或萌芽。
【注】将用这道题为例给大家展示为什么在马克总主义哲学中,会强调“真理与语误可以相互转化”,也隐藏着以后会显露出来的真理的成分或萌芽。

其实错误的解法是由内而外拉格朗日。正确的解法是由外而内拉格朗日。
套路四 具体问题具体分析

虽然前面已经讲过公式法,但公式也并不是万能的,此类题我们需要观紧式子结构,去分析你要证明的结论是哪个函数求导以后的样子,然后尝试将其还原。
总之,还原出辅助函数
 的过程是朝着熵减的方向前进,所以有困难是正常的!
的过程是朝着熵减的方向前进,所以有困难是正常的!








【注】本题应说明,分母为何不为0。








伪双中值问题!



















套路五 分离常数和中值,直接拉或柯西





此题为上一专题 套路四的例2







套路六 双中值定理【虚假的双中值】


【注】以此题为例,总结出一套组合拳,通杀——
- ① 将复杂的中值分离出来
- ② 将其还原
- ③ 恒等变形或带入条件
- ④ 再用一次中值定理或柯西
- ⑤ 战斗结束
【三中值例题】








套路七 【真正的双中值定理】
对于结论中同时含有
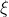 和
和 两个中值的问题,若题干明确了
两个中值的问题,若题干明确了 ,则上面的方法无效!因为上述方法中的
,则上面的方法无效!因为上述方法中的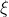 和
和  取自同一个区间
取自同一个区间 ,所以无法保证它们不同!
,所以无法保证它们不同!为了解决这个问题,需要在
![\left [ a,b\right ]](https://1000bd.com/contentImg/2022/06/26/161355341.gif) 中插入分段点
中插入分段点 ,将区间
,将区间![\left [ a,b\right ]](https://1000bd.com/contentImg/2022/06/26/161355341.gif) 拆分为
拆分为![[a,c],[c,b]](https://1000bd.com/contentImg/2022/06/26/161357797.gif) ,在两个区间上分别用一次中值定理,得到
,在两个区间上分别用一次中值定理,得到 ,由于两个区间都没有交集,自然保证了
,由于两个区间都没有交集,自然保证了 。
。故显然,这种问题中区间分段点
 到底选在哪里是非常重要的,我们往往需要使用待定系数法进行“倒推”,分析出分段点需要满足的条件!(但不一定两个中值点都在区间内,有可能是某个端点,如例4、类题4)
到底选在哪里是非常重要的,我们往往需要使用待定系数法进行“倒推”,分析出分段点需要满足的条件!(但不一定两个中值点都在区间内,有可能是某个端点,如例4、类题4)





【n中值问题】


【例4:三个中值也可以取自两个区间】


【补充】这些不同的中值不一定来源于不同的区间,也有可能是一个来源于开区间内部,而另外一个来源于区间端点,这类题目很有意思,比如下面这道类题。
【类题前 铺垫一下~ 不然可能不会挖掘题目条件】



套路八 求中值θ的极限

套路 四部曲:重新展开,对比两式、建立等式,分离中值θ,求极限。



【注】没展干净,等式两边不能同除。







【例4 下面这道题,虽然也是计算
 的极限,但是由于
的极限,但是由于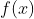 的表达式已知,所以我们可以轻松地从题干中反解出
的表达式已知,所以我们可以轻松地从题干中反解出  的表达式,毫无难度】
的表达式,毫无难度】
【错误解法】



【正确解法】

套路九 泰勒中值定理
若欲证结论中含有高阶导(二阶导以上):一般可以采用“带拉格朗日余项的泰勒展开”进行证明。再具体操作中,最重要的是恰当的 选取展开点
 和 被展开点
和 被展开点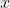 的位置。
的位置。一般而言,选取导数信息多的点作为展开点,选取只告诉函数值的点作为被展开点。
- 套路:
- 有限区间:在端点展开,或在中点展开
- 无限区间:在任意点展开
注意:




【注】
本题需要用到 连续函数 介值定理的一个推论:

其中
![\xi\in [x_{1},x{_2}]](https://1000bd.com/contentImg/2022/06/26/161419472.gif) ,或
,或![\xi\in [x_{2},x{_1}]](https://1000bd.com/contentImg/2022/06/26/161421040.gif)
由于“导函数天生满足介值定理”,故条件中的“三阶导数连续”可以改为“三阶可导”!!
【例2 :极值点蕴含了导数的信息,所以常常将函数在极值点处展开】




注:

接下来的两道题,题干条件均未告知经历点处的函数值和导数值,所以也只有根据结论来猜测展开点和被展开点该如何选取。





经验:在 “中间点”展开

例4:在一条笔直的道路上,一辆汽车从开始启动到刹车停止,共用了单位时间走完了单位路程.。证明:至少有一个时刻,其加速度的绝对值不少与 4。


【注】对于这种 “两个端点的函数值,导数值均已知” 的题,为了充分利用已知条件,初学者可能会选择两端点处相互展开,但这样误差会很大(因为泰勒展开本身就是估计,它要求展开点与被展开点的距离不需太大),所以采用中点在端点处展开。
利用上面的注意事项,便可轻松秒杀下面这道题。



【注】泰勒+任一点处展开。


开始无穷区间咯 ~



资料来自 考研竞赛凯哥 ~
泰勒中值定理,看这个视频,足够了!!!_哔哩哔哩_bilibili
自用 整理~
题目源自(谢谢学长~
- 1、若
-
相关阅读:
Spring源码:SpringBean 的注册-XML源码解析
腾讯云2023年双11优惠活动和9999元代金券领取规则
文本输入编辑框 EditText
【微服务】Nacos的优势
【视觉SLAM14讲】【汇总】
内存屏障(Memory Barrier)
linux 笔记:远程服务器登录jupyter notebook
你不一定知道的四种遍历进程的方法(c语言)
通知机制程序代码_java培训
2022年最新辽宁建筑八大员(电气施工员)模拟题库及答案
- 原文地址:https://blog.csdn.net/weixin_47187147/article/details/125415824