C题-Helping the Nature

思路

• 直接的思路：使得每棵相邻树的高度相同。做法只能是对每棵相邻的树，根据大小处理前缀或后缀之一，相同高度为两者的较小值，且这些处理序列一个也不能少。
• 差分的思路（转）：
  其中$d_1=a[1]-a[0]$,其中$a[0]=0$

看到区间操作就想到前缀和和差分。属于常用套路

#include <bits/stdc++.h>
using namespace std;
#include<stack>
#define int long long
signed main()
{
    int t;
    cin >> t;
    for(int i = 0;i<t;i++)
    {
        int n;
        cin >> n;
        int a[n];
        for(int k = 0;k<n;k++) cin>>a[k];
        int ans = 0;
        int temp = a[n - 1];
        for(int k = n - 1;k>=1;k--)
        {
            if(a[k] - a[k - 1] >= 0)  //后缀相减使其等于前缀
            {
                ans += (a[k] - a[k - 1]);
                temp -= (a[k] - a[k - 1]);
            }
            else
            {
                ans += (a[k - 1] - a[k]);
            }
        }
        cout << ans + abs(temp) << endl;
    }
    system("pause");
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

D题-Helping The Nature

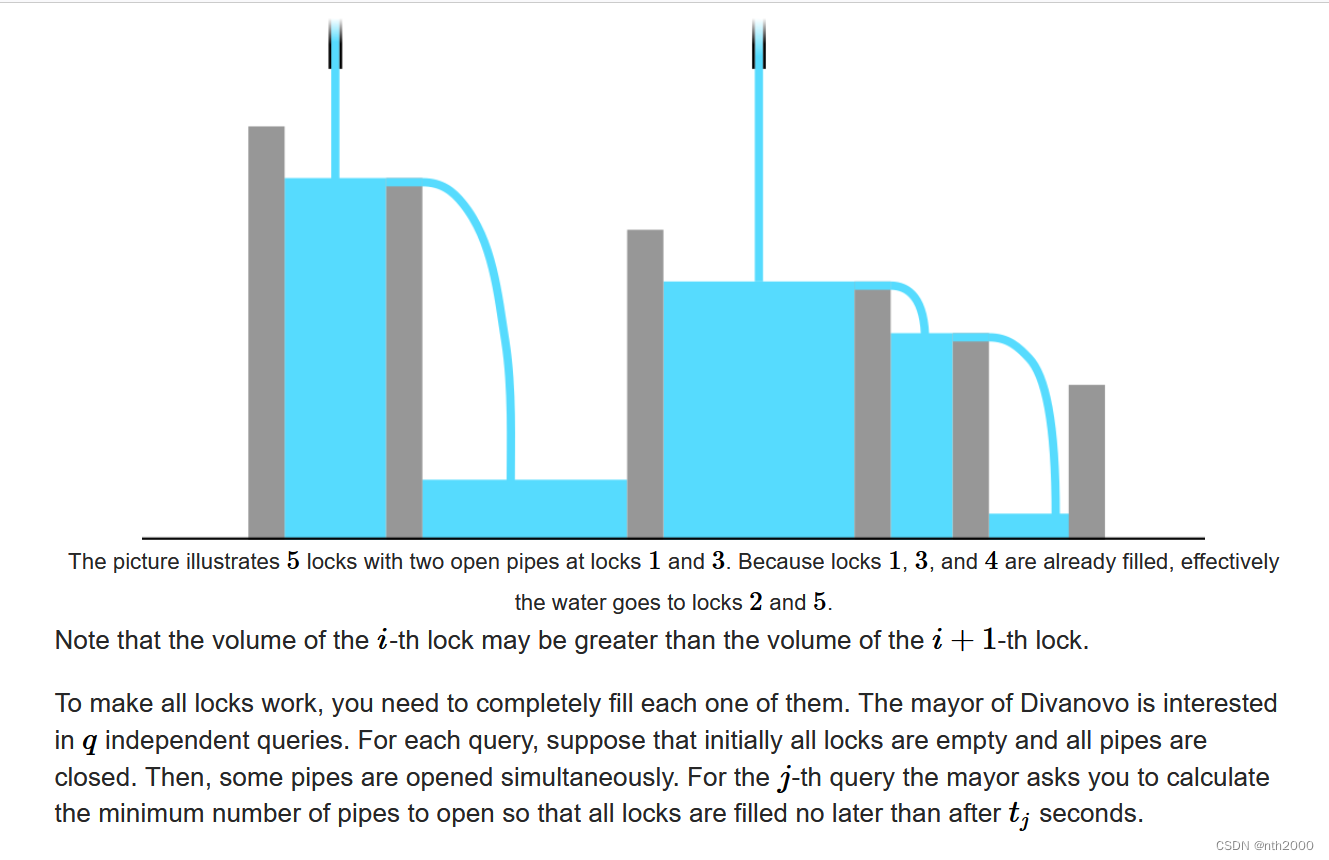
思路

• 必要条件减小搜索空间
• 找是否能满足DP

设$DP[i]$，处理到第i个lock，前i个lock全部开启，并装满前i个lock所需要的最短时间。guess:

• 若第i个lock能在前面i-1个lock装满的时间之前或刚好装满，则$DP[i]=DP[i-1]$
• 否则，前i-1个lock溢出的水与第i个lock管道的水会相互混合。可看作是前i个管道向前i个lock注水。所需时间$\lceil \frac{sum(v[1:i])}{i}\rceil$

所以$$DP[i]=max(DP[i-1],\lceil \frac{sum(v[1:i])}{i}\rceil )$$
对每个query,必要条件是$t_{query}>=dp[n]$.在这样的时间段内，若取q个管道,可保证有充足的时间将这前q个装满。

• 若开启前q个管道而在$dp[n]$的时间内所有水库已经装满，则q一定满足条件。且一定有$t_{query}\cdot q\ge dp[n]\cdot q\ge sum(v[1:n])$
• 否则可看作前q的管道同时注水，速率混合。因此需要保证在$t_{query}$的时间内，以q速率，能将水库注满，也有：$t_{query}\cdot q\ge sum(v[1:n])$

因此给定q，只需检查
$$t_{query}\cdot q\ge sum(v[1:n])$$是否满足即可。找到最小这样的q即可。

#include <bits/stdc++.h>
using namespace std;
#include<stack>
#define int long long
signed main()
{
    int n;
    cin >> n;
    int v[n];
    int prev[n + 1];
    prev[0] = 0;
    for(int i = 0;i<n;i++) 
    {
        scanf("%ld",&v[i]);
        prev[i + 1]  = prev[i] + v[i];
    }
    int dp[n + 1];
    dp[1] = v[0];
    for(int i = 2;i<=n;i++) dp[i] = max(dp[i - 1],(long long)ceil((double)prev[i] / i));
    int q;
    cin >> q;
    for(int i = 0;i<q;i++)
    {
        int t;
        scanf("%ld",&t);
        if(t < dp[n]) printf("-1\n");
        else   //找到第一个大于等于ceil(prev[n]/t)的prefixsum之和
        {
            t = (int)ceil((double)prev[n]/t);
            printf("%ld\n",t);
        }
    }
    system("pause");
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34