-
【论文阅读|深读】DRNE:Deep Recursive Network Embedding with Regular Equivalence
目录

前言
Hello!
非常感谢您阅读海轰的文章,倘若文中有错误的地方,欢迎您指出~
自我介绍 ଘ(੭ˊᵕˋ)੭
昵称:海轰
标签:程序猿|C++选手|学生
简介:因C语言结识编程,随后转入计算机专业,获得过国家奖学金,有幸在竞赛中拿过一些国奖、省奖…已保研。
学习经验:扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语!
唯有努力💪
知其然 知其所以然!
本文仅记录自己感兴趣的内容ABSTRACT
网络嵌入的目的是在嵌入空间中保持顶点的相似性
现有的方法通常通过节点之间的直接连接或共同邻域来定义相似性,即结构等价
然而,位于网络不同部位的顶点可能具有相似的角色或位置,即正则等价,这一点在网络嵌入文献中基本被忽略。
正则等价是用递归的方式定义的,即两个正则等价顶点具有同样正则等价的网络邻居。
因此,我们提出了一种新的深度递归网络嵌入方法来学习具有规则等价的网络嵌入。
更具体地说,我们提出了一个层规范化的LSTM,通过递归地聚合它们的邻域表示来表示每个节点。
我们从理论上证明了一些流行的、典型的、符合规则等价的中心性测度是我们模型的最优解。
1 INTRODUCTION
有多种方法来量化网络中顶点的相似性。最常见的是结构等效[18]。
如果两个顶点共享许多相同的网络邻居,那么它们在结构上是等价的。
以往关于网络嵌入的研究大多旨在通过高阶近邻来保持结构等价性[33,35]
将网络邻居扩展为高阶近邻,如直接近邻、近邻的近邻等(嵌套循环)。
然而,在许多情况下,顶点具有相似的角色或占据相似的位置,而没有任何公共邻居。例如:
两位母亲与丈夫和几个孩子的关系模式相同。
虽然如果两位母亲没有相同的亲属,她们在结构上并不对等,但她们确实扮演着相似的角色或职位。这些情况使我们得到了顶点相似的扩展定义,称为正则等价。
如果两个顶点的网络邻居本身相似(即规则等价),则它们被定义为规则等价
显然,规则等价是结构等价的一种松弛。结构等价保证了规则等价,但相反的方向不成立。
相比之下,规则对等更灵活,能够覆盖与结构角色或节点重要性相关的广泛的网络应用,但在很大程度上被网络嵌入的文献所忽视。
为了保持网络嵌入中的正则等价,即两个正则等价节点应该具有相似的嵌入。
一种简单的方法是显式计算所有顶点对的正则等价,并要求节点嵌入的相似性来近似其对应的正则等价。
但对于大规模网络来说,这是不可行的,因为计算规则等值的复杂性很高。
另一种选择是将常规等价替换为更简单的图论度量,例如中心性度量。
虽然已经设计了许多中心性度量来表征顶点的角色和重要性,但一个中心性只能捕捉网络角色的特定方面,这使得学习一般的和任务无关的节点嵌入变得困难。更不用说一些中心性度量,如中间性中心性,也具有很高的计算复杂性
如何在网络嵌入中有效、高效地保持正则等价仍然是一个有待解决的问题。
如前所述,正则等价的定义是递归的。这启发了我们以递归的方式学习网络嵌入,即一个节点的嵌入是通过它的邻居的嵌入聚合的
在一个递归步骤中(如图1所示),如果节点3和5、4和6、7和8规则等价,因此已经具有类似的嵌入,则节点1和2将具有类似的嵌入,从而导致它们的规则等价为真。
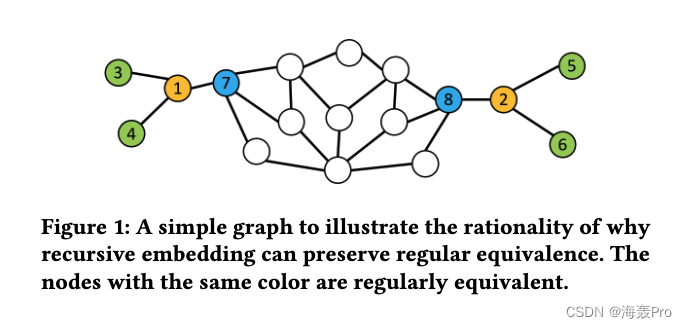
正是基于这种思想,我们提出了一种新的深度递归网络嵌入(DRNE)方法。
更具体地说
- 我们将节点的邻居转换为有序序列
- 并提出了一种层归一化LSTM
- 以非线性的方式将邻居的嵌入聚合到目标节点的嵌入中。
我们从理论上证明了一些流行的和典型的中心性度量是我们模型的最优解。
实验结果还表明,学习的节点表示能够很好地保持成对正则等价,并预测每个节点的多个中心性度量的值。
本文有以下贡献:
- 我们研究了一个新的具有正则等价的节点表示学习问题,这是网络分析中的关键问题,但在网络表示学习的文献中被很大程度上忽略了。
- 我们找到了一种将全局正则等价相关信息融入到节点表示中的有效方法,并提出了一种新的深层模型DRNE,该模型通过以非线性的方式递归聚集邻居的表示来学习节点表示。
- 我们从理论上证明了所学习的节点表示能够很好地保持成对正则等价,并反映了几种流行的和典型的节点中心性。实验结果还表明,该方法在结构角色分类中明显优于中心性度量方法和其他网络嵌入方法。
2 RELATED WORK
现有的大多数网络嵌入方法都是沿着保持观察到的成对相似性和结构等价的路线发展的。
- DeepWalk[28]使用随机行走从网络中生成节点序列,并利用语言模型通过将序列视为句子来学习节点表示
- Node2vec[12]扩展了这一思想,提出了一个有偏二阶随机游走模型
- LINE[33]优化了一个目标函数,旨在保持节点的两两相似性和结构等价。
- M-NMF[36]将更宏观的结构——社区结构纳入到嵌入方法中
- Structural Deep Network Embedding 声称网络的底层结构是高度非线性的,并提出了一个深度自编码器模型,以保持网络结构的一阶和二阶邻近性。
- Label informed attributed network embedding & Attributed network embedding for learning in a dynamic environment:将节点属性加入到网络中,平滑地将属性信息和拓扑结构嵌入到低维表示中
- RolX[13]为节点枚举各种手工制作的结构特征,并为这个关节特征空间找到更适合的基向量
- 类似地,struc2vec[29]通过定义某种形式的中心性启发式来衡量结构相似性,对中心性相似性的显式计算使其不可扩展
在学习表示时,这些方法都不能保持规则等价
规则对等作为结构对等的一种放宽的概念,可以更好地捕捉结构信息
- REGE[7]和CATREGE[7]是通过迭代搜索两个顶点邻居的最优匹配来实现的
- VertexSim[18]利用线性代数的递归方法构造相似性测度。但由于规则等价的计算复杂度高,这在大规模网络中是不可行的
中心性度量是衡量网络中节点结构信息的另一种方法
为了研究如何更好地捕捉结构信息,提出了一组中心性[3,20,21]
由于它们中的每一个只捕获结构信息的一个方面,某种中心性不能很好地支持不同的网络和应用程序
此外,设计中心性度量的手工方式使得它们不太全面,无法纳入常规等效相关信息综上所述,对于学习具有规则等价的节点表示,仍然没有很好的解决方案
3 DEEP RECURSIVE NETWORK EMBEDDING
DRNE整体框架图
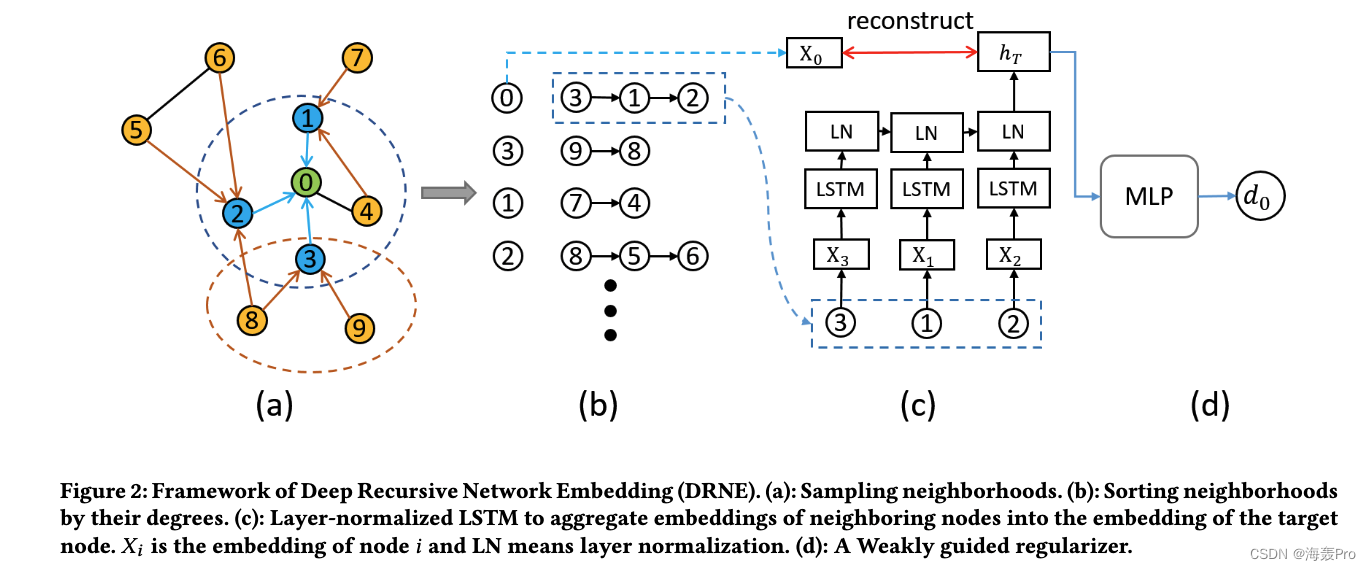
- (a)采样邻域
- (b)排序邻域中的节点(按照度)
- (c)层归一化LSTM,将相邻节点的嵌入聚合到目标节点的嵌入中。 X i X_i Xi为节点i的嵌入, L N LN LN为层归一化
- (d)弱引导正则化器
图中步骤的理解:
- (a)以节点0为例,我们先对它邻居节点123进行采样
- (b)按degree进行排序形成一个序列(312)
- (c)用该领域序列 X 3 , X 2 , X 1 X_3,X_2,X_1 X3,X2,X1的嵌入向量作为输入,通过单层normalized LSTM得到整合的表示 h T h_T hT ,通过 h T h_T hT 重构嵌入向量 X 0 X_0 X0和节点 0 0 0,嵌入的向量 X 0 X_0 X0能够良好的保留局部领域性质。
- (d)另一方面,我们可以用度 d 0 d_0 d0 作为中心衡量的弱监督信息,将 h T h_T hT输入到多层感知器MLP中,以近似得到 d 0 d_0 d0 。对网络中的其他节点执行同样的过程。当我们更新 X 3 , X 1 , X 2 X_3,X_1,X_2 X3,X1,X2时,节点 0 0 0的嵌入 X 0 X_0 X0也会随之更新。通过反复的迭代更新重复这个过程,那么嵌入的 X 0 X_0 X0就可以包含整个网络的机构信息
参考:https://zhuanlan.zhihu.com/p/104488503
3.1 Notations and Definitions
G = ( V , E ) G=(V,E) G=(V,E)
N ( v ) = { u ∣ ( v , u ) ∈ E } N(v)=\{u| (v,u)\in E\} N(v)={u∣(v,u)∈E}
X = R ∣ V ∣ × k \boldsymbol X= \mathbb{R}^{|V| \times k} X=R∣V∣×k:顶点的嵌入空间向量表示
d v = ∣ N ( v ) ∣ d_v=|N(v)| dv=∣N(v)∣:顶点 v v v的度
I ( x ) = { 1 x ≥ 0 0 e l s e I(x)=
I(x)={1x≥00else
Definition 3.1 (Structural Equivalence)
- s ( u ) = s ( v ) s(u) = s(v) s(u)=s(v) : 节点 u u u和 v v v是结构等价
- N ( u ) = N ( v ) ⇒ s ( u ) = s ( v ) N(u) = N(v) \Rightarrow s(u) = s(v) N(u)=N(v)⇒s(u)=s(v)
- 也就是节点的邻域相同,则为结构等价
Definition 3.2 (Regular Equivalence)
- r ( u ) = r ( v ) r(u) = r(v) r(u)=r(v):节点 u u u和 v v v是正则等价
- { r ( i ) ∣ i ∈ N ( u ) } = { r ( j ) ∣ j ∈ N ( u ) } \{r(i)|i\in N(u)\}=\{r(j)|j\in N(u)\} {r(i)∣i∈N(u)}={r(j)∣j∈N(u)}(没懂)
3.2 Recursive Embedding
根据定义3.2,我们以递归的方式学习节点嵌入,目标节点的嵌入可以用其邻居节点嵌入的聚合来近似
基于此概念,我们设计了如下损失函数:
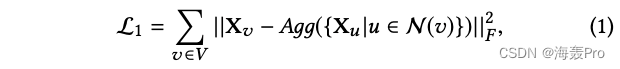
其中Agg是聚合函数
在一个递归步骤中,学习到的嵌入节点可以保留其邻居的局部结构
通过迭代更新学习到的表示,学习到的节点嵌入可以在全局意义上融合其结构信息,这与规则等价的定义是一致的
由于真实网络的底层结构往往是高度非线性的[22],我们设计了一个深度模型,归一化长短时记忆层(ln-LSTM)[2]作为聚合函数
众所周知,LSTM对序列建模是有效的。然而,节点的邻居在网络中没有自然排序
这里我们使用节点的度作为将邻居排序成有序序列的标准
- 主要是因为度是邻居排序的最有效的度量
- 而度在许多图论度量中往往起着重要的作用,特别是那些与结构角色相关的度量,如PageRank[27]和Katz[25]
设
- 有序邻域的嵌入为 { X 1 , X 2 , … , X t , … , X T } \{X_1,X_2,…,X_t,…,X_T\} {X1,X2,…,Xt,…,XT}
- 在每个时间步长 t t t时,隐态 h t h_t ht是 t t t时刻的输入嵌入 X t X_t Xt与其之前的隐态 h t − 1 h_{t−1} ht−1的函数,即 h t = L S T M C e l l ( h t − 1 , X t ) h_t = LSTMCell(h_{t−1},X_t) ht=LSTMCell(ht−1,Xt)
当LSTM Cell对嵌入序列进行从1到T的递归处理时,隐含表示 h t h_t ht的信息会越来越丰富
h T h_T hT可以看作是邻居的聚集表示。
为了学习长序列中的长距离相关性,LSTM利用了门控机制
- 遗忘门决定我们要从记忆中丢弃什么信息
- 输入门和旧记忆一起决定我们要在记忆中存储什么新信息
- 输出门根据记忆决定我们要输出什么
具体来说,LSTM跃迁方程LSTMCell为:
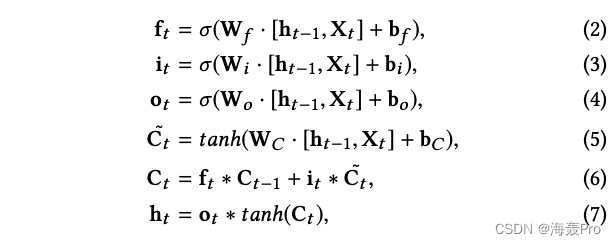
此外,为了避免以长序列为输入的梯度[14]爆炸或消失的问题,我们还引入了层归一化层归一化的LSTM使其不变地重新缩放所有的求和输入。它产生了更稳定的动力学
特别是,它在方程6后使用额外的归一化使细胞状态 C t C_t Ct居中并重新缩放,如下所示:
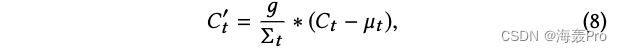
3.3 Regularization
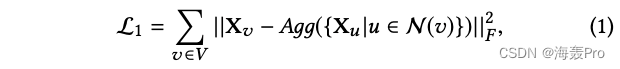
(1)式是按照定义3.2的递归嵌入过程,没有任何其他约束。
它具有很强的表达能力,只要满足给定的递归过程,就可以推导出多个解。
该模型退化为所有嵌入值为0的平凡解是有风险的
为了避免出现平凡解,我们将节点的度作为弱引导信息,并设置一个约束条件
- 即学习的节点嵌入必须能够近似节点的度。
据此,我们设计了以下正则化器:
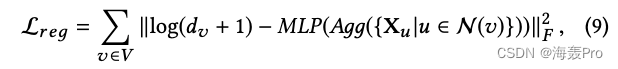
其中- d v d_v dv是节点 v v v的度
- M L P MLP MLP是单层多层感知器,具有整流线性单元(ReLU)[11]激活,其定义为 R e L U ( X ) = m a x ( 0 , x ) ReLU(X)=max(0,x) ReLU(X)=max(0,x)
总而言之,我们通过组合公式1的重构损失和公式9的正则化来最小化目标函数:
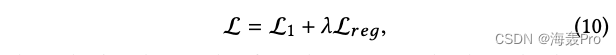
其中
- λ λ λ是正则化的权重
注意
- 这里不使用度信息作为网络嵌入的监督信息。
- 相反,它最终起到辅助作用,使解决方案远离微不足道的解决方案。
- 因此,这里的 λ λ λ是一个相当小的值。
Neighborhood Sampling
在现实网络中,节点的度往往服从重尾分布[9],即少数节点的度很高,而大多数节点的度很小
在Ln-LSTM算法中,为了提高算法的效率,在输入LN-LSTM之前,我们对节点的邻域进行了大次数的下采样。
具体地说,我们设置了邻居数S的上界,如果邻居数超过上界S,我们将它们下采样为S个不同的节点。
在幂律网络中,度大的节点比度小的普通节点携带更多独特的结构信息。

为此,我们设计了一种有偏采样策略:
- 通过设置节点 v v v的采样概率 P ( v ) P(v) P(v)与其度数 d v d_v dv成正比
- P ( v ) ∝ d v P(v)∝d_v P(v)∝dv来保持节点的大阶数
3.4 Optimization
为了优化前述模型,目标是最小化作为神经网络参数集θ和嵌入X的函数的总损失L(等式10)
Adam[16]被用来优化这些参数(使用Adam算法进行求解)
- 利用时间反向传播(BackPropagation Through Time, BPTT)算法[37]估计导数
- 在训练开始时,Adam的学习速率α初始设定为0.0025
论文:Adam: A Method for Stochastic Optimization
3.5 Theoretical Analysis
我们进一步从理论上证明 D R N E DRNE DRNE的结果嵌入可以很好地反映几个典型的和常见的中心性度量,这些中心性度量与规则等价密切相关
在不丧失一般性的情况下,我们忽略方程9中用于避免平凡解的正则项。
定理3.3. 度中心性、特征向量中心性[5]、PageRank中心性[27]分别是我们模型的三个最优解。
利用引理3.4进行证明
引理3.4 对于任何可计算函数,都存在一个有限递归神经网络[24]来计算它。
证明过程略(看不懂)
定理3.5. 如果节点 v v v的中心性 C ( v ) C(v) C(v)满足 C ( v ) = ∑ u ∈ N ( u ) F ( u ) C ( u ) C(v) =\sum_{u\in N(u)}F(u)C(u) C(v)=∑u∈N(u)F(u)C(u) and F ( u ) = f ( { F ( u ) , u ∈ N ( v ) } ) F(u) = f (\{F (u), u∈N(v)\}) F(u)=f({F(u),u∈N(v)}),其中 F F F是任意可计算函数,那么 C ( v ) C(v) C(v)就是我们模型的最优解之一
证明过程略(看不懂)
通过 ( F ( v ) , f ( { x i } ) ) (F(v), f(\{x_i\})) (F(v),f({xi}))在表1中对中心性的定义,我们可以很容易地得到度中心性、特征向量中心性、PageRank中心性满足定理3.5的条件,从而完成了定理3.3的证明。

根据定理3.3,对于任何图,我们提出的方法都存在这样一个参数设置,即学习到的嵌入可以是三个中心性之一
这证明了我们的方法在捕获与规则等价相关的网络结构信息的不同方面的表达能力。
3.6 Analysis and Discussions
在本节中,我们将介绍样本外扩展和复杂性分析。
3.6.1 Out-of-sample Extension
对于一个新到达的节点 v v v,如果已知它与现有节点的连接,我们可以直接将其邻居的嵌入输入到聚合函数中,用式1得到作为该节点嵌入的聚合表示。
该过程的复杂度为 O ( d v k ) O(d_vk) O(dvk)
- k k k为嵌入的长度,
- d v d_v dv为节点 v v v的度。
3.6.2 Complexity Analysis
在训练过程中,对于每次迭代的单个节点 v v v,计算梯度和更新参数的时间复杂度为 O ( d v k 2 ) O(d_v k^2) O(dvk2)
d v d_v dv为节点 v v v的度, k k k为嵌入的长度
由于采样过程的原因, d v d_v dv度不会超过限定的数值S。因此整体训练复杂度为 O ( ∣ V ∣ S k 2 I ) O(|V|Sk^2I) O(∣V∣Sk2I)
I I I为迭代次数
其它参数的设置
- 嵌入的长度 k k k通常设置为一个较小的数字,如32,64,128。
- S设为300。迭代次数 I I I通常很小,但与节点数 ∣ V ∣ |V| ∣V∣无关
因此,训练过程的复杂度与节点数 ∣ V ∣ |V| ∣V∣成线性关系。
4 EXPERIMENTS
4.1 Baselines and Parameter Settings
基线方法
- DeepWalk
- LINE
- node2vec
- struc2vec
- Centralities:采用近中心性[26]、中间中心性[4]、特征向量中心性[6]和K-core[17]这四种常用的中心性来衡量节点的重要性。此外,我们将之前的四个中心性连接到一个向量中作为另一个基线(Combined)
参数设置
对于我们的模型,我们设置
- 嵌入长度 k k k为16
- 正则化器的权值 λ λ λ为1
- 有限邻域数 S S S为300
我们将在4.5节中说明我们的模型对这些参数不是很敏感
4.2 Network Visualization
杠铃网络可视化
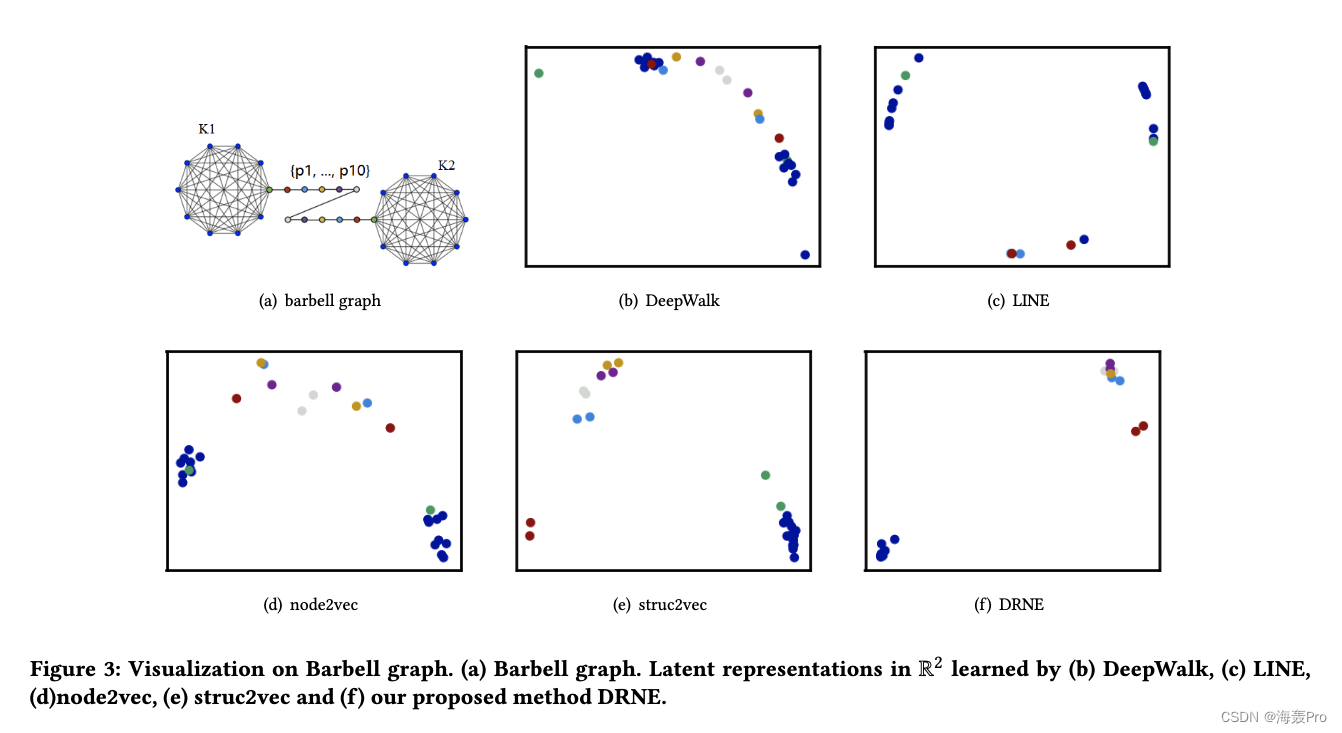
空手道网络可视化
4.3 Regular Equivalence Prediction
在本节中,我们评估学习到的嵌入是否在两个真实世界的数据集上保持规则等价
数据集
- Jazz[10]
- BlogCatalog [38]
在这里我们设置了两个任务,包括规则等价性预测和中心性评分预测
对于第一个任务,我们使用常用的基于规则等价的相似性度量方法VS[18]作为基础真值。
两个节点的两两相似度由其嵌入的内积来衡量。
我们根据节点对的相似性对其进行排序,并将结果排序与VS. Kendall排序进行比较
使用[1]秩相关系数来衡量这两个秩的相关性。其定义如下:
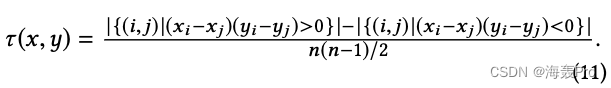
结果如图5所示: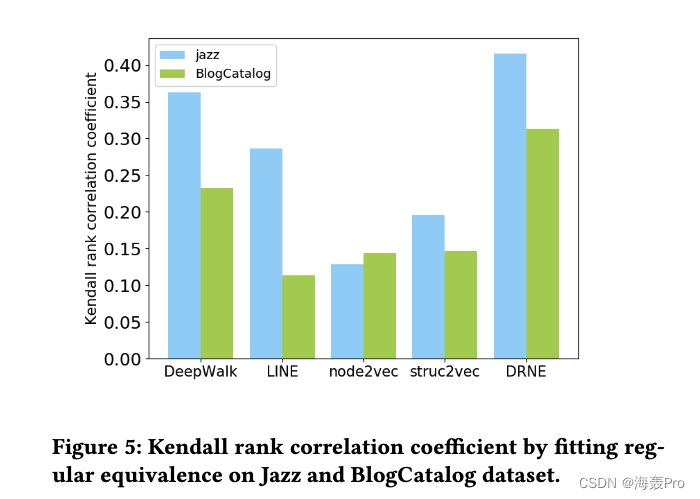
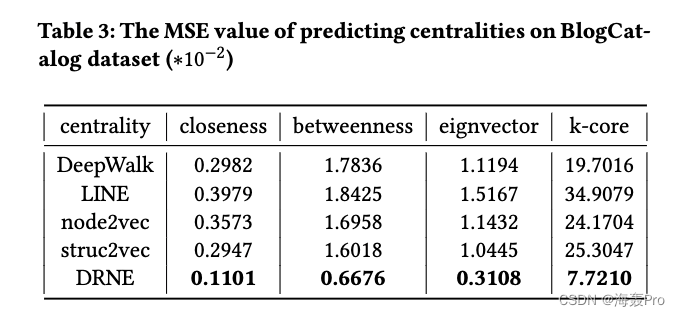
对于第二个任务,我们将4.1节中提到的四个中心性作为基准来计算
然后随机隐藏20%的节点,利用剩余的节点训练线性回归模型,基于节点嵌入预测中心性得分
训练后,我们使用回归模型来预测被屏蔽节点的中心性
采用均方误差(Mean Square Error, MSE)评价其性能。MSE定义如下:

其中 Y Y Y为观测值, Y ^ \hat Y Y^为预测值。由于不同中心性的尺度存在显著差异,我们将MSE值除以相应的所有节点中心性的平均值来重新缩放。
结果如表2、表3所示。
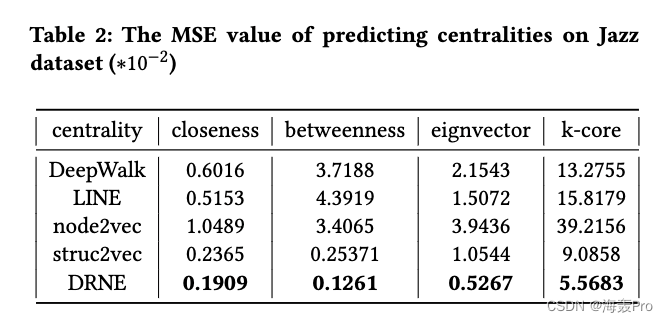
4.4 Structural Role Classification
基于结构角色的分类任务中,节点的标签与其结构信息的关联比与其相邻节点的标签的关联更大。
在本节中,我们评估学习嵌入在预测给定网络中节点的结构角色的能力。
数据集:欧洲航空交通网络和美国航空交通网络[29]
节点表示机场,边表示直航的存在。
降落加起飞的总人数或通过机场的总人数可以用来衡量他们的活动,反映他们在航班网络中的结构角色。
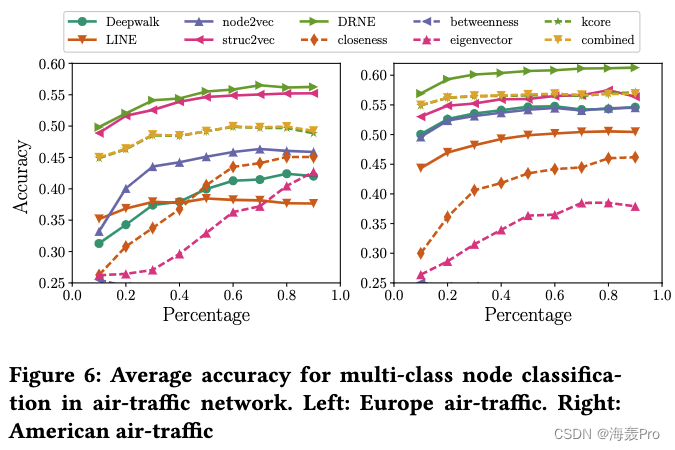
通过将每个机场的活动分布均匀地划分为四个可能的标签之一。在得到机场的嵌入后,我们训练一个逻辑回归来预测基于嵌入的标签
我们随机抽取10% ~ 90%的节点作为训练样本,使用剩余的节点来测试性能。
平均精度用于评估性能。
结果如图6所示,其中实线表示网络嵌入方法,虚线表示中心性方法。
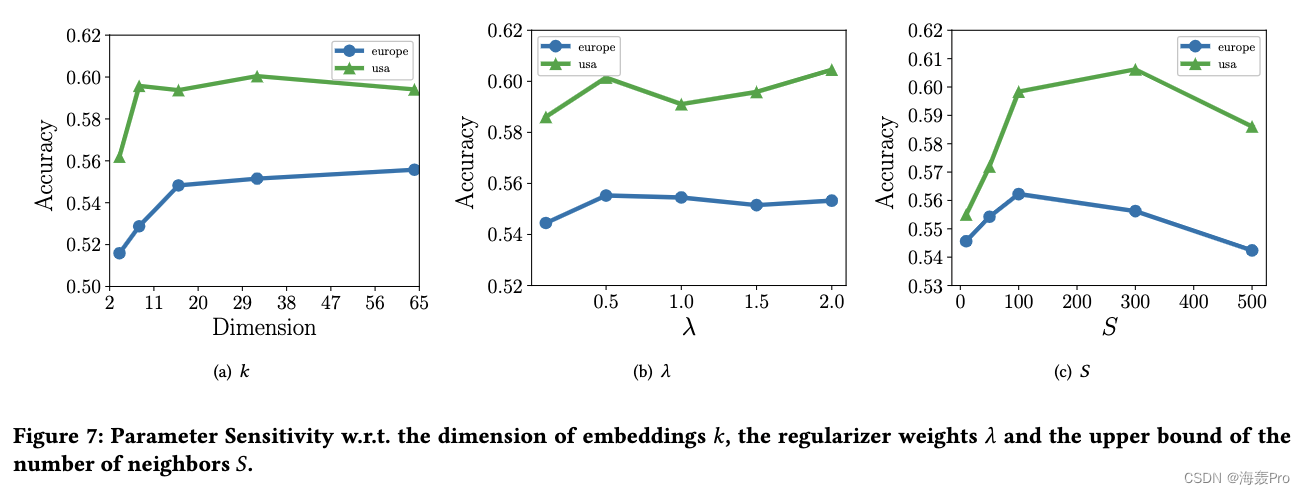
4.5 Parameter Sensitivity
我们评估了嵌入维数 k k k、正则化器权重 λ λ λ和邻域大小上界 S S S的影响
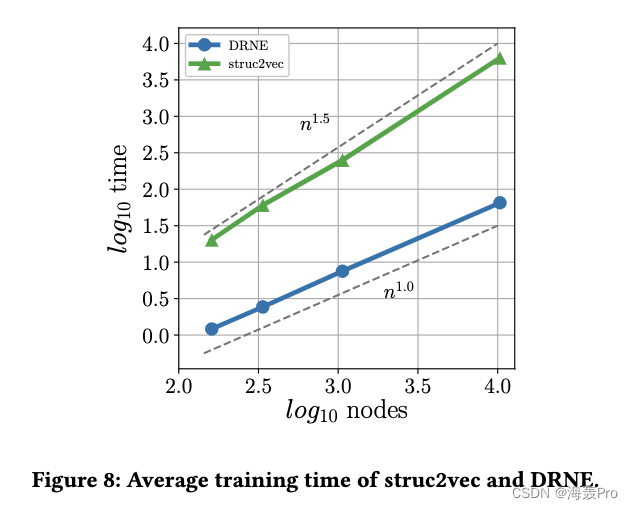
4.6 Scalability
为了证明可扩展性,我们测试每个epoch的训练时间
结果如图8所示
5 CONCLUSION
在本文中,我们提出了一个新的深度模型来学习网络中具有规则等价性的节点表示。
假设节点的规则等价信息已被其相邻节点的表示编码,我们提出一层归一化LSTM模型递归学习节点嵌入。
对于给定的节点,远距离节点的结构重要性信息可以递归地传播到相邻节点,从而嵌入到其嵌入中。
因此,学习到的节点嵌入能够在全局意义上反映节点的结构信息,这与规则的等价性和中心性度量是一致的。
实证结果表明,我们的方法可以显著和持续地优于最先进的算法。
读后总结
整体思路大概了解了
但是由于对LSTM的不了解
细节上的东西还是没有理解到
若以后需要仔细探究,再仔细研究研究!
结语
文章仅作为个人学习笔记记录,记录从0到1的一个过程
希望对您有一点点帮助,如有错误欢迎小伙伴指正

-
相关阅读:
strongswan:configure: error: OpenSSL Crypto library not found
ORAN C平面 Section Extension 23
基于windows WSL安装Docker Desktop,修改默认安装到C盘及默认下载镜像到C盘
IPV4和IPV6,公网IP和私有IP有什么区别?
FCOS相关
推荐系统在腾讯游戏运营中的实践
sql同表分组取第一条
限制命令长度如何反弹shell
【scipy 基础】--聚类
【netty】什么是netty
- 原文地址:https://blog.csdn.net/weixin_44225182/article/details/125441285