题目链接： https://leetcode.com/problems/permutations/

1. 题目介绍（Permutations）

Given an array nums of distinct integers, return all the possible permutations. You can return the answer in any order.

【Translate】： 给定一个由不同整数组成的数组，返回所有可能的排列。你可以以任何顺序返回答案。

【测试用例】：

【约束】：

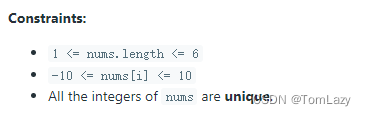
2. 题解

2.1 递归+交换数字

  原代码来自孙靖俊的Java实现全排列，主要思想就是通过不停的递归，不减少数组中的元素，使用两个指针start和end来控制范围来进行数组元素的交换。以[1,2,3]为例，依次是[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,2,1],[3,1,2]]。

class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> permutations = new ArrayList<>();
        perm(nums,0,nums.length-1,permutations);
        return permutations;
    }
    
    public static void perm(int[] array,int start,int end,List<List<Integer>> permutations) {
        
        if(start==end) {
        	// int[] 转 list<Integer>
            permutations.add(Arrays.stream(array).boxed().collect(Collectors.toList()));
        } else {
            for (int i = start; i <= end; i++) {
            	//1，2，3的全排列这块相当于将其中一个提了出来，下次递归从start+1开始
                swap(array,start,i);
                perm(array,start+1,end,permutations);
                //这块是复原数组，为了保证下次另外的同级递归使用数组不会出错
                //这块可以通过树来理解，每次回退一步操作，交换回去
                swap(array,start,i);
            }         
        }
    }
    public static void swap(int[] array,int i,int j) {
        int temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

2.2 Permutations II (contains duplicates)

  issac3的题解 A general approach to backtracking questions in Java (Subsets, Permutations, Combination Sum, Palindrome Partioning)，其中包含 Subsets, Permutations,Combination Sum, and Palindrome Partitioning 的常见回溯题解。

class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> list = new ArrayList<>();
        Arrays.sort(nums);
        backtrack(list, new ArrayList<>(), nums, new boolean[nums.length]);
        return list;
    }

    private void backtrack(List<List<Integer>> list, List<Integer> tempList, int [] nums, boolean [] used){
        if(tempList.size() == nums.length){
            list.add(new ArrayList<>(tempList));
        } else{
            for(int i = 0; i < nums.length; i++){
                if(used[i] || i > 0 && nums[i] == nums[i-1] && !used[i - 1]) continue;
                used[i] = true; 
                tempList.add(nums[i]);
                backtrack(list, tempList, nums, used);
                used[i] = false; 
                tempList.remove(tempList.size() - 1);
            }
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

3. 参考资料

[1] Java实现全排列
[2] 如何在 Java 中把一个数组转换为一个列表
[3] int []数组与List互相转换