-
浅谈二叉树
目录
1.树型结构
树是一种 非线性 的数据结构,它是由 n ( n>=0 )个有限结点组成一个具有层次关系的集合。 把它叫做树是因为它看 起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的 。它具有以下的特点:1) 有一个特殊的节点,称为根节点,根节点没有前驱节点2) 除根节点外,其余节点被分成 M(M > 0) 个互不相交的集合 T1 、 T2 、 ...... 、 Tm ,其中每一 个集 合 Ti (1 <= i <= m) 又是一棵与树类似的子树。每棵子树的根节点有且只有一个驱, 可以有 0 个或多个后继3) 树是递归定义的。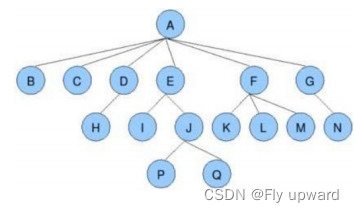
1.1 定义
节点的度 :一个节点含有的子树的个数称为该节点的度; 如上图: A 的为 6树的度 :一棵树中,最大的节点的度称为树的度; 如上图:树的度为 6叶子节点或终端节点 :度为 0 的节点称为叶节点; 如上图: B 、 C 、 H 、 I... 等节点为叶节点双亲节点或父节点 :若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图: A 是 B 的父节点孩子节点或子节点 :一个节点含有的子树的根节点称为该节点的子节点; 如上图: B 是 A 的孩子节点根结点 :一棵树中,没有双亲结点的结点;如上图: A节点的层次 :从根开始定义起,根为第 1 层,根的子节点为第 2 层,以此类推树的高度或深度 :树中节点的最大层次; 如上图:树的高度为 4非终端节点或分支节点 :度不为 0 的节点; 如上图: D 、 E 、 F 、 G... 等节点为分支节点兄弟节点 :具有相同父节点的节点互称为兄弟节点; 如上图: B 、 C 是兄弟节点堂兄弟节点 :双亲在同一层的节点互为堂兄弟;如上图: H 、 I 互为兄弟节点节点的祖先 :从根到该节点所经分支上的所有节点;如上图: A 是所有节点的祖先子孙 :以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是 A 的子孙森林 :由 m ( m>=0 )棵互不相交的树的集合称为森林1.2 树的表示形式
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,实际中树有很多种表示方式,如:双亲表示法, 孩子表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的孩子兄弟表示法 。- class Node {
- int value; // 树中存储的数据
- Node firstChild; // 第一个孩子引用
- Node nextBrother; // 下一个兄弟引用
- }
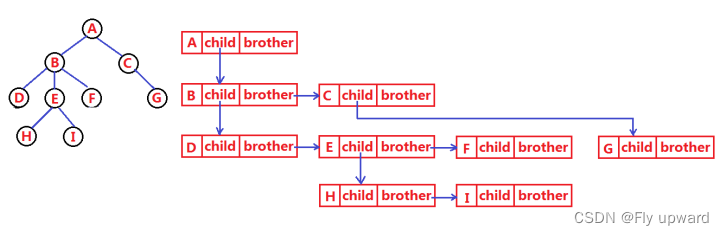
1.3 树的应用
多用于文件系统管理:目录和文件
2.二叉树定理
2.1 概念
一棵二叉树是结点的一个有限集合,该集合或者为空,或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。二叉树的特点:
1. 每个结点最多有两棵子树,即二叉树不存在度大于 2 的结点。2. 二叉树的子树有左右之分,其子树的次序不能颠倒,因此二叉树是有序树。注意:对于任意的二叉树都有以下情况复合而成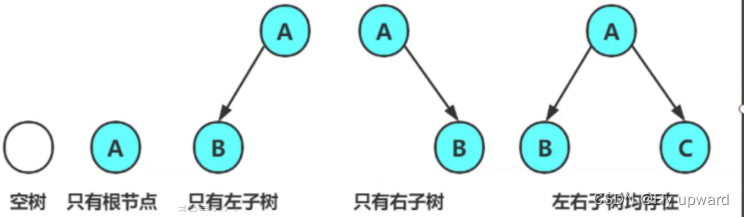
2.2 两种特殊的二叉树
1. 满二叉树 : 一个二叉树,如果 每一个层的结点数都达到最大值,则这个二叉树就是满二叉树 。也就是说, 如果 一个二叉树的层数为 K ,且结点总数是2^k - 1 ,则它就是满二叉树 。 2. 完全二叉树 : 完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n 个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一 一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
2. 完全二叉树 : 完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n 个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一 一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
2.2 二叉树的性质
1. 若规定 根节点的层数为 1 ,则一棵 非空二叉树的第 i 层(深度)上最多有2^i - 1 (i>0) 个结点.2. 若规定只有 根节点的二叉树的深度为 1 ,则 深度为 K 的二叉树的最大结点数是 2^k - 1 (k>=0)3. 对任何一棵二叉树 , 如果其 叶结点个数为 n0, 度为 2 的非叶结点个数为 n2, 则有 n0 = n2 + 14. 具有 n 个结点的完全二叉树的深度 k 为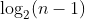 上取整
5. 对于具有 n 个结点的完全二叉树 ,如果按照 从上至下从左至右的顺序对所有节点从 0 开始编号 ,则对于 序号为 i 的结点有 :若i>0 , 双亲序号: (i-1)/2 ; i=0 , i 为根节点编号 ,无双亲节点若 2i+1<n ,左孩子序号: 2i+1 ,否则无左孩子若 2i+2<n ,右孩子序号: 2i+2 ,否则无右孩子
上取整
5. 对于具有 n 个结点的完全二叉树 ,如果按照 从上至下从左至右的顺序对所有节点从 0 开始编号 ,则对于 序号为 i 的结点有 :若i>0 , 双亲序号: (i-1)/2 ; i=0 , i 为根节点编号 ,无双亲节点若 2i+1<n ,左孩子序号: 2i+1 ,否则无左孩子若 2i+2<n ,右孩子序号: 2i+2 ,否则无右孩子2.3 二叉树的存储
二叉树的存储结构 分为: 顺序存储 和 类似于链表的链式存储二叉树的链式存储是通过一个一个的节点引用起来的,常见的表示方式有二叉和三叉表示方式 ,具体如下:- // 孩子表示法
- class Node {
- int val; // 数据域
- Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
- Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
- }
- // 孩子双亲表示法
- class Node {
- int val; // 数据域
- Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
- Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
- Node parent; // 当前节点的根节点
- }
2.6 二叉树的遍历
遍历 (Traversal) 是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问 。 访问结点所做的操作 依赖于具体的应用问题 ( 比如:打印节点内容、节点内容加 1) 。 遍历是二叉树上最重要的操作之一,是二叉树上进行其它运算之基础。根据遍历根节点的先后次序有以下遍历方式:1. 前序遍历 (Preorder Traversal 亦称先序遍历 )—— 根结点 ---> 根的左子树 ---> 根的右子树。2. 中序遍历 (Inorder Traversal)—— 根的左子树 ---> 根节点 ---> 根的右子树。3. 后序遍历 (Postorder Traversal)—— 根的左子树 ---> 根的右子树 ---> 根节点。第一颗二叉树
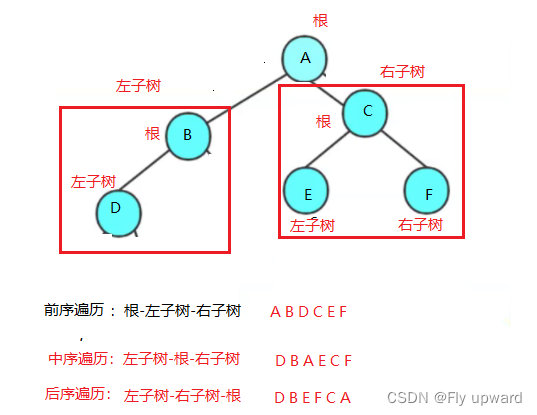
第二课二叉树

在前、中、后遍历中,使用递归方法都是要打印根。
1)前序遍历
解法一
- void preOrder(BTNode root) {
- if(root == null) {
- return;
- }
- System.out.print(root.val + " ");
- preOrder(root.left);
- preOrder(root.right);
- }
解法二:非递归法
- void preorderNor(TreeNode root) {
- List<Integer> ret = new ArrayList<>();
- Stack<TreeNode> stack = new Stack();
- TreeNode cur = root;
- while (cur != null || stack.isEmpty()) {
- while (cur != null) {
- //进栈
- stack.push(cur);
- //将栈元素进顺序表
- ret.add(cur.val);
- cur = cur.left;
- }
- TreeNode top = stack.pop();
- cur = top.right;
- }
- return ret;
- }
2)中序遍历
解法一
- void inOrder(BTNode root) {
- if(root == null) {
- return;
- }
- inOrder(root.left);
- System.out.print(root.val + " ");
- inOrder(root.right);
- }
解法二:非递归法
- void inorderNor(TreeNode root) {
- List<Integer> ret = new ArrayList<>();
- Stack<TreeNode> stack = new Stack();
- TreeNode cur = root;
- while (cur != null || stack.isEmpty()) {
- while (cur != null) {
- //进栈
- stack.push(cur);
- cur = cur.left;
- }
- TreeNode top = stack.pop();
- //将栈顶元素进顺序表
- ret.add(top.val);
- cur = top.right;
- }
- return ret;
- }
3)后序遍历
解法一
- //后序遍历
- void postOrder(BTNode root) {
- if(root == null) {
- return;
- }
- postOrder(root.left);
- postOrder(root.right);
- System.out.print(root.val + " ");
- }
解法二 :非递归法
- void inorderNor(TreeNode root) {
- List<Integer> ret = new ArrayList<>();
- Stack<TreeNode> stack = new Stack();
- TreeNode cur = root;
- TreeNode prev = null;
- while (cur != null || stack.isEmpty()) {
- while (cur != null) {
- //进栈
- stack.push(cur);
- cur = cur.left;
- }
- //读取栈顶元素
- TreeNode top = stack.peek();
- if () {
- stack.pop();
- ret.add(top.val);
- prev = top;
- }else {
- cur = top.right;
- }
- }
- return ret;
- }
注意:
知道先序遍历和 中序遍历,找后序遍历:
先从先序遍历最前面拿到根,然后拿着根在中序遍历的序列中找到此根,根的左边是左子树,根的右边是右子树。依次循环。
知道后序遍历和 中序遍历,找后序遍历:
先从后序遍历最后面拿到根,然后拿着根在中序遍历的序列中找到此根,根的左边是左子树,根的右边是右子树。依次循环。
2.7 层序遍历
设二叉树的根节点所在层数为 1 ,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从 左到右访问第2 层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是 层序遍历。- public List<List<Integer>> levelOrder(TreeNode root) {
- List<List<Integer>> ret = new ArrayList<>();
- if (root == null) return ret;
- Queue<TreeNode> queue = new LinkedList<>();
- queue.offer(root);
- while (!queue.isEmpty) {
- int size = queue.size();//当前层有多少个节点
- List<Integer> lst = new ArrayList<>();
- while (size != 0) {
- TreeNode cur = queue.poll();
- list.add(cur.val);
- if (cur.left != null) {
- queue.offer(cur.left);
- }
- if (cur.right != null) {
- queue.offer(cur.right);
- }
- size--;
- }
- ret.add(list);
- }
- return ret;
- }
-
相关阅读:
PyTorch创始人:开源成功的方法论
EtherCAT转Modbus-TCP协议网关与DCS连接的配置方法
Qt编写物联网管理平台36-通信协议
DFS与DFT的关系,以及DFT与DCT的关系
vue3 封装 naive input 组件
java计算机毕业设计课程与成绩管理源码+mysql数据库+系统+lw文档+部署
Chrome扩展程序开发随记
MySQL索引在关联查询中的作用
使用 sqlc 生成类型安全的Go代码与SQL数据库交互
【cmake】彻底弄懂cmake中的可见性/传递性 INTEFACE 问题
- 原文地址:https://blog.csdn.net/m0_60494863/article/details/125310510