-
数学建模——非线性规划
目录
非线性规划:描述目标函数或约束条件条件的数学表达式中,至少有一个是非线性函数。
基本概念
记
![x=[x_{1},x_{2},...,x_{n}]^{T}](https://1000bd.com/contentImg/2022/06/26/075521806.gif) 是n维欧式空间
是n维欧式空间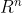 中的一个点(n维向量),
中的一个点(n维向量),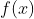 ,
,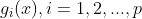 ,
,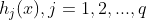 是定义在
是定义在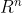 上的实值函数。若f,g,h函数中至少有一个是x的非线性函数,则称如下为非线性规划模型的一般形式:
上的实值函数。若f,g,h函数中至少有一个是x的非线性函数,则称如下为非线性规划模型的一般形式: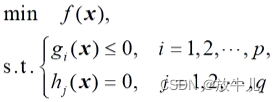
全局最优解:若
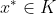 ,并且
,并且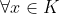 都有
都有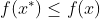 ,则称
,则称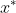 为全局最优解。
为全局最优解。局部最优解:x的邻域内(也包含于可行域),x所对应的函数值是最小的,则x为局部最优解。
无约束非线性规划问题可以具体表示为:
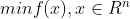
凸规划
凸规划是一类特殊的非线性规划问题,可以求得全局最优解。
凸集:

凸函数:

定义在凸集上的有限个凸函数的非负线性组合仍为凸函数
判别定理


半正定矩阵的行列式非负。
黑塞矩阵:
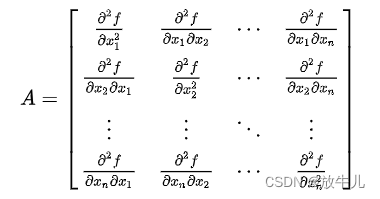
对于非线性规划模型的一般形式,若f(x)为凸函数,g(x)为凸函数,h(x)为线性函数,则称该非线性规划问题为凸规划。凸规划局部最优解即为全局最优解,最优解的集合形成一个凸集。当目标函数为严格凸函数时,其最优解必定唯一。
例子

f(x)和g2(x)的黑塞矩阵的行列式:
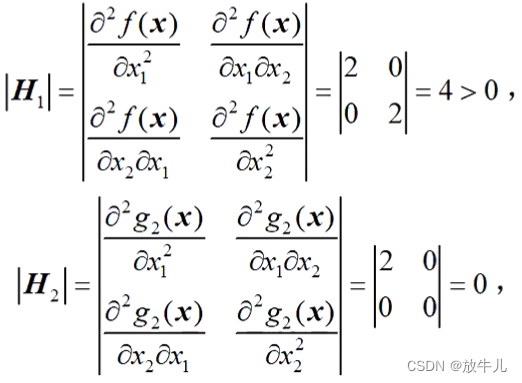
其他约束条件为线性函数,所以是一个凸规划问题
- clc,clear
- prob = optimproblem;
- x = optimvar('x',2,'LowerBound',0);
- prob.Objective = sum(x.^2)-4*x(1)+4;
- con = [-x(1)+x(2)-2 <= 0
- x(1)^2-x(2)+1 <= 0];
- prob.Constraints.con = con;
- x0.x = rand(2,1)%非线性规划必须赋初值,x0名字随便取
- [s,f,flag,o] = solve(prob,x0);
- s.x
ans =
0.5536
1.3064二次规划模型
目标函数是关于决策向量的二次函数,约束条件是线性的,则该模型称为二次规划模型,一般形式:


其中:
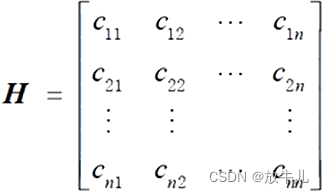
当H正定时,目标函数最小化时,模型为凸二次规划,凸二次规划局部最优解就是全局最优解。如果不是凸规划,则建议使用fmincon函数。
例子
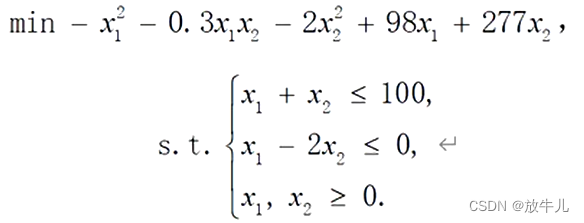
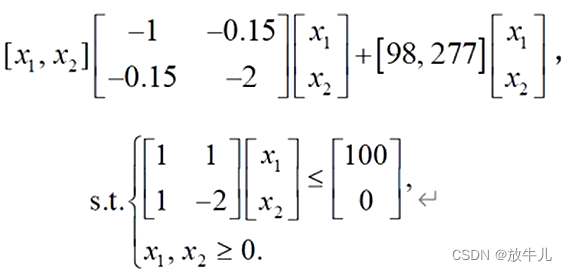
目标函数是最小化,但是H为负定矩阵,所以不是凸规划。
- clc,clear
- x = optimvar('x',2,'LowerBound',0);
- h = [-1,-0.15;-0.15,-2];
- f = [98;277];
- a = [1,1;1,-2];
- b = [100;0];
- prob = optimproblem('Objective',x'*h*x+f'*x);
- prob.Constraints = a*x <= b;
- [s,f,flag,o] = solve(prob);
- s.x
ans =
1
1[1,1]是局部最优解,使用fmincon函数:
- fx = @(x)x'*h*x+f'*x;
- [x,y] = fmincon(fx,rand(2,1),a,b,[],[],[0;0],[])
x =
1.0e-07 *
0.2533
0.3400
y =1.1901e-05
非线性规划的求解
无约束极值问题
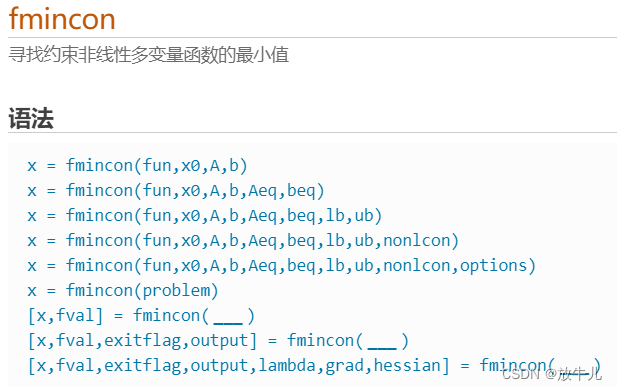
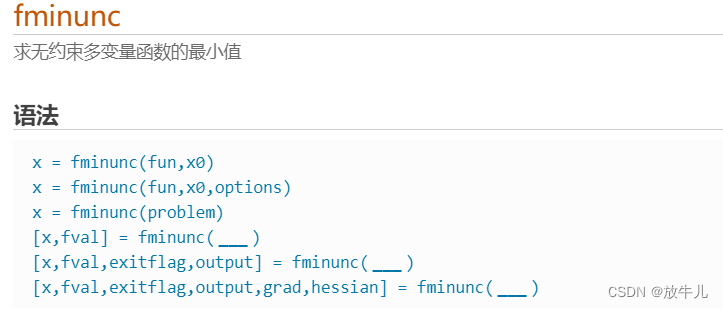
MATLAB工具箱中用于求解无约束极小值的函数有:

例子
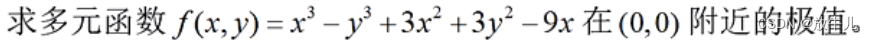
- clc,clear
- f = @(x) x(1)^3-x(2)^3+3*x(1)^2+3*x(2)^2-9*x(1);
- g = @(x) -f(x);
- [m1,n1] = fminunc(f,[0,0])%求极小值
- [m2,n2] = fminsearch(g,[0,0]);%求极大值
- m2,-n2
m1 =
1.0000 -0.0000
n1 =-5
m2 =-3.0000 2.0000
ans =31.0000

有约束极值问题
同样有基于求解器的求解方法和基于问题的求解方法
基于求解器的解法
数学模型的标准形式为:


例:

- clc,clear
- fun1 = @(x) sum(x.^2)+8;
- [x,y] = fmincon(fun1,rand(3,1),[],[],[],[],zeros(3,1),[],@fun2)
- function [c,ceq] = fun2(x)
- c = [-x(1)^2+x(2)-x(3)^2
- x(1)+x(2)^2+x(3)^3-20];
- ceq = [-x(1)-x(2)^2+2
- x(2)+2*x(3)^2-3];
- end
基于问题的求解
- clc,clear
- x = optimvar('x',3,'LowerBound',0);
- prob = optimproblem('Objective',sum(x.^2)+8);
- con1 = [-x(1)^2+x(2)-x(3)^2 <= 0
- x(1)+x(2)^2+x(3)^3 <= 20];
- con2 = [-x(1)-x(2)^2+2 == 0
- x(2)+2*x(3)^2 == 3];
- prob.Constraints.con1 = con1;
- prob.Constraints.con2 = con2;
- x0.x = rand(3,1);
- [s,f,flag,out] = solve(prob,x0);
- s.x,f
其他
匿名函数的返回值只能有一个,可以是向量。
-
相关阅读:
discuz怎么转wordpress,详细实操过程
【TCP套接字编程,UDP套接字编程】
【洛谷 P1048】[NOIP2005 普及组] 采药 题解(动态规划+01背包)
一起学数据结构(11)——快速排序及其优化
Django国际化与本地化指南
大学生旅游风景主题dreamweaver网页设计大作业-陕西渭南HTML+CSS制作网页
机器人机械臂抓取综述
【算法 | 概述初识】时间复杂度和空间复杂度(我不信看完这篇文章你还不懂)
C# GetMethod 方法应用实例
论文-分布式-并发控制-Lamport逻辑时钟
- 原文地址:https://blog.csdn.net/m0_51311105/article/details/125411850