读《vue3设计与实现》2- vue的diff算法核心

第9章简单的diff算法

在第8章中，patch更新时候，如果新旧节点都是数组的情况，当时采用把旧节点全部清除，然后完全重新添加新节点，这样可以实现目标，但是性能不佳。本章开始介绍vue的渲染器核心diff算法，简单来说就是新旧vnode节点的子节点都是一组节点的情况下，以最小性能开销完成更新操作。

9.1减少DOM操作的性能开销

有如下结构的新旧虚拟节点：

// 旧vnode
const oldVnode = {
  type: "div",
  children: [
    {type: "p", children:1},
    {type: "p", children:2},
    {type: "p", children:3}
  ]
}

// 新vnode
const newVnode = {
  type: "div",
  children: [
    {type: "p", children:4},
    {type: "p", children:5},
    {type: "p", children:6}
  ]
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

按照第8章的做法：

• 卸载所有旧节点，需要3次DOM删除操作
• 挂载所有新的子节点，需要3次DOM添加操作

这样完成目标需要6次操作DOM，性能不佳。通过观察可以发现，新旧node的子节点，之后children内容不同，可以通过算法实现只更新内容，这样就可以只需操作3次DOM就能达到目的，性能会提升一倍。
重新调整patchChildren函数

function patchChildren(n1, n2, container) {
  if(typeof n2.children === "string"){
    // ...
  } else if(Array.isArray(n2.children)){
    // 重新实现两组子节点的更新方式
    const oldChildren = n1.children;
    const newChildren = n2.children;
    // 遍历旧的children
    for(let i = 0; i< oldChildren.length; i++){
      //调用patch函数更新子节点
      patch(oldChildren[i], newChildren[i])
    }
  }else{
    //...
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

oldChildren和newChildren分别代表旧的子节点和新的子节点，并将2组对应位置的节点分别传递给patch函数进行更新。patch函数在执行更新时，发现新旧子节点只有文本内容不同，只会更新文本节点内容。
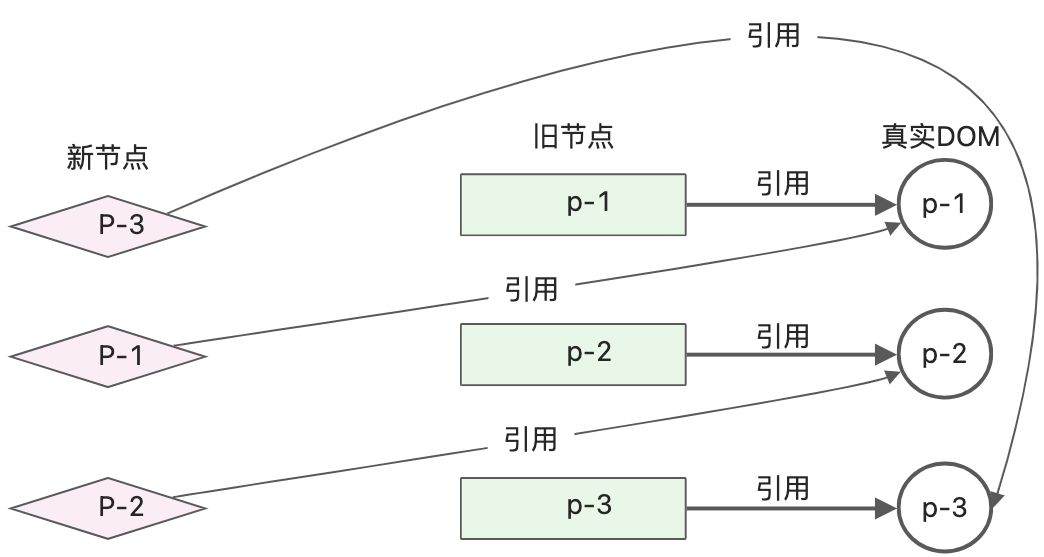
用示意图展示更新过程，菱形表示新子节点，矩形表示旧的子节点，圆形表示真实的DOM节点。

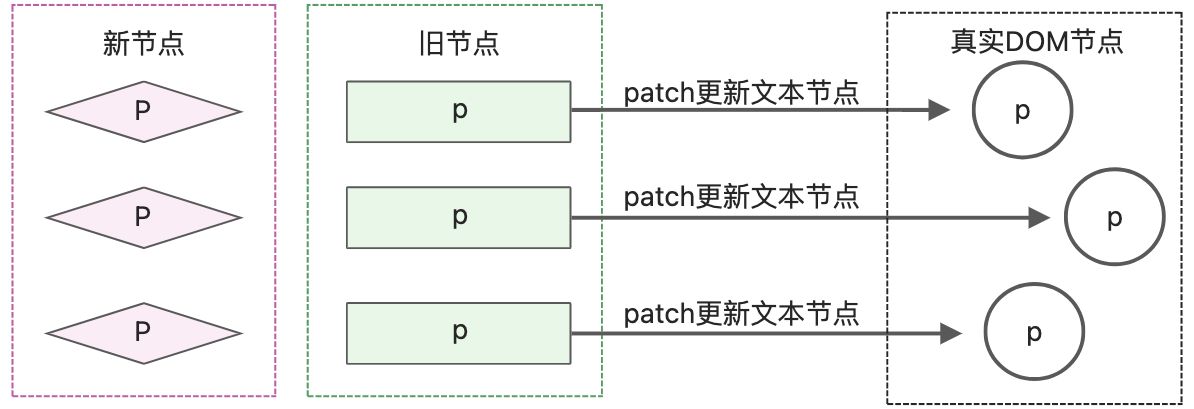
这种做法减少了操作DOM的次数，但是当新旧子节点数量不同，会存在问题。新的子节点多，无法正常添加新节点，新的节点少，无法删除旧的子节点。

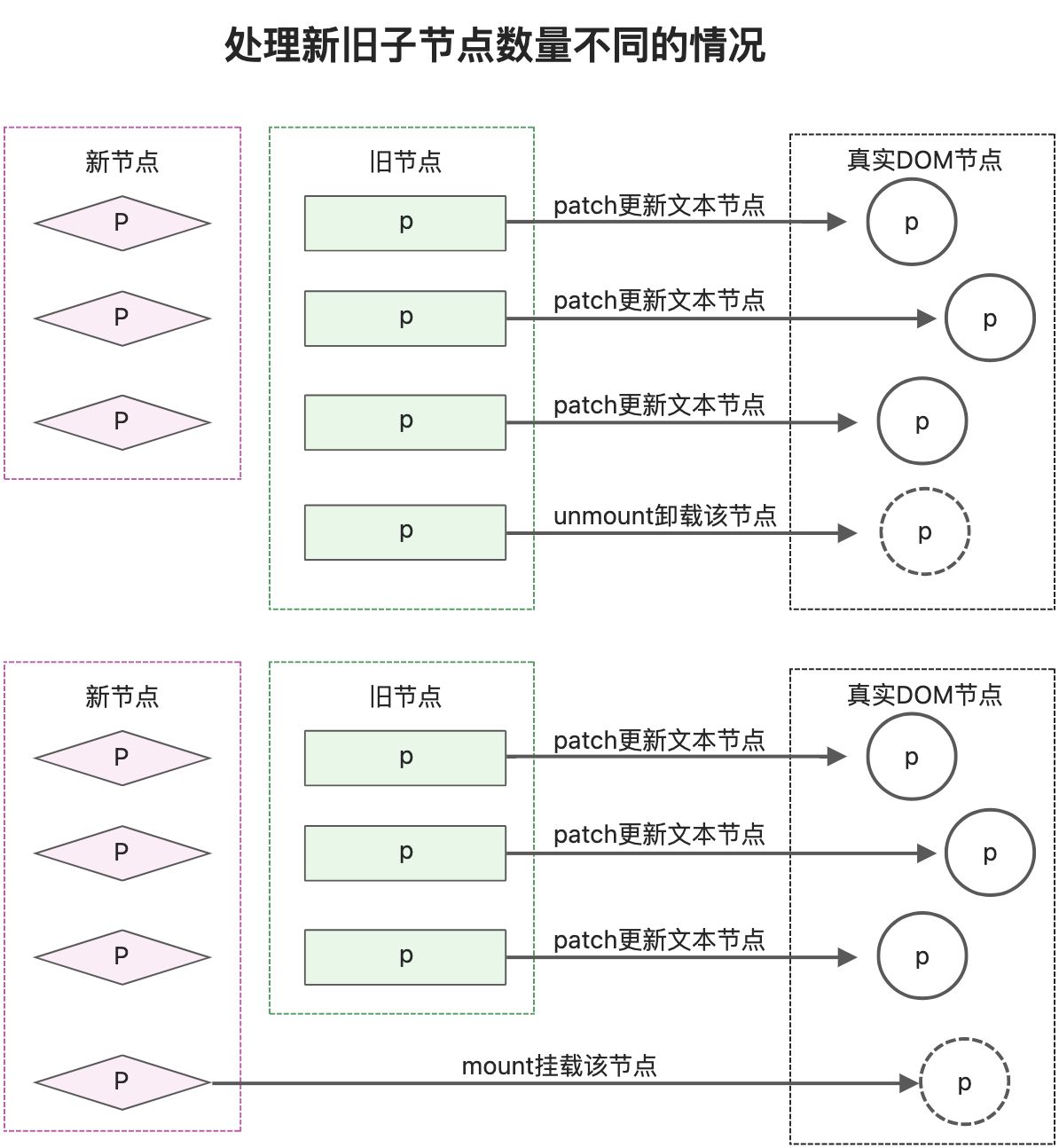
通过分析，在新旧两组子节点更新是，不能固定变量新的子节点或旧的子节点，而是应该遍历长度短的那一组，然后在接着比对新旧2组子节点的长度，如果新的子节点更长，说明有新节点要添加，否则就是旧的子节点要卸载。

function patchChildren(n1, n2, container) {
  if (typeof n2.children === 'string') {
    if (Array.isArray(n1.children)) {
      n1.children.forEach((c) => unmount(c))
    }
    setElementText(container, n2.children)
  } else if (Array.isArray(n2.children)) {
    const oldChildren = n1.children
    const newChildren = n2.children
    const oldLen = oldChildren.length
    const newLen = newChildren.length
    const commonLength = Math.min(oldLen, newLen)
    for (let i = 0; i < commonLength; i++) {
      patch(oldChildren[i], newChildren[i])
    }
    // 如果 nextLen > prevLen，将多出来的元素添加
    if (newLen > oldLen) {
      for (let i = commonLength; i < newLen; i++) {
        patch(null, newChildren[i], container)
      }
    } else if (oldLen > newLen) {
      // 如果 prevLen > nextLen，将多出来的元素移除
      for (let i = commonLength; i < oldLen; i++) {
        unmount(oldChildren[i])
      }
    }
  } else {
    if (Array.isArray(n1.children)) {
      n1.children.forEach(c => unmount(c))
    } else if (typeof n1.children === 'string') {
      setElementText(container, '')
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

代码示例

9.2DOM复用和Key的作用

diff算法的核心就是减少操作DOM的次数，提升性能。
使用上节的方式，仍存在优化空间，有如下新旧2组子节点

// oldChildren
[{type:"p"}, {type:"div"}, {type:"span"}]

// newChildren
[{type:"span"}, {type:"p"}, {type:"div"}]
1
2
3
4
5

如果使用上节的patchChildren算法，仍需要6次DOM操作。
但其实通过观察可以发现，新旧子节点只是顺序不同，最好的处理方式是，移动DOM来完成子节点的更新。
接下来就该处理如何确定新的子节点是否出现在旧的一组子节点中。仅仅通过判断type类型可以吗？其实这是不行的，如果子节点的类型都是p，那么就完全相同，是否就不需要移动更新呢，这样会出现bug。

// oldchildren
[
  { type: 'p', children: '1', key: 1 },
  { type: 'p', children: '2', key: 2 },
  { type: 'p', children: 'hello', key: 3 }
]
// newChildren
[
  { type: 'p', children: 'world', key: 3 },
  { type: 'p', children: '1', key: 1 },
  { type: 'p', children: '2', key: 2 }
]
1
2
3
4
5
6
7
8
9
10
11
12

这时就需要使用到key属性，key是节点的身份标识，通过key可以对比新旧子节点是否相同。

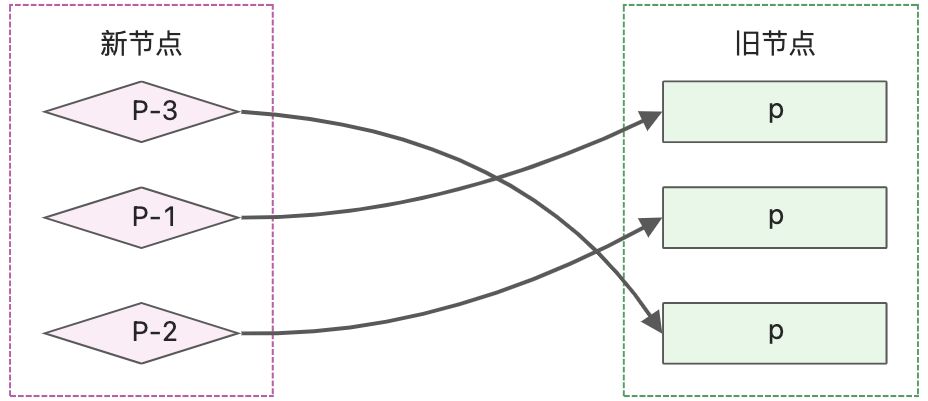
通过key属性可以明确知道新子节点在旧子节点中的位置，就可以进行对应的DOM移动操作。

function patchChildren(n1, n2, container) {
  if (typeof n2.children === 'string') {
    if (Array.isArray(n1.children)) {
      n1.children.forEach((c) => unmount(c))
    }
    setElementText(container, n2.children)
  } else if (Array.isArray(n2.children)) {
    const oldChildren = n1.children
    const newChildren = n2.children

    // 遍历新的 children
    for (let i = 0; i < newChildren.length; i++) {
      const newVNode = newChildren[i]
      let j = 0
      // 遍历旧的 children
      for (j; j < oldChildren.length; j++) {
        const oldVNode = oldChildren[j]
        // 如果找到了具有相同 key 值的两个节点，则调用 `patch` 函数更新
        // 节点相同，内容或属性可能已经发生变化
        if (newVNode.key === oldVNode.key) {
          patch(oldVNode, newVNode, container)
          break // 这里需要 break
        }
      }
    }
    
  } else {
    if (Array.isArray(n1.children)) {
      n1.children.forEach(c => unmount(c))
    } else if (typeof n1.children === 'string') {
      setElementText(container, '')
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

第19行通过对比节点的key是否相同，来判断节点是否是同一个节点。如果是同一个节点，执行patch打补丁操作后直接跳出循环。
在代码中使用了双层for循环，外层循环用于遍历新的一组子节点，内层循环则遍历旧的一组子节点。找到相同节点则进行patch打补丁操作。经过这一步操作能够保证所有可复用的节点本身都更新完毕。
执行完毕后，key为3的元素仍显示在最后，下一步就需要找出需要移动的DOM元素，进行移动。

注意⚠️：这里的双层for循环，性能是极差的，在实际项目中无法使用。

代码示例

9.3找出需要移动的元素

通过key对比出相同节点可以复用，但是没有进行移动。要想进行移动，第一步需要找出要移动的节点，第二步进行移动操作。
本节目标是找出需要移动的节点元素。
什么情况下需要移动操作呢，肯定是新旧子节点元素的顺序发生了变化。

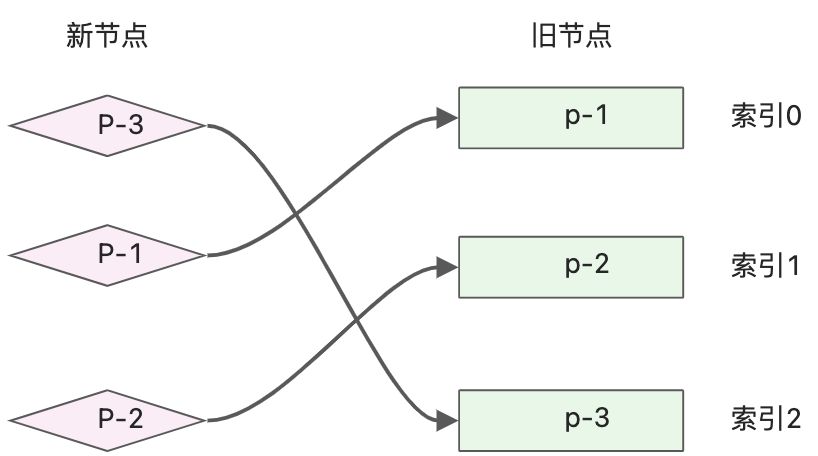
上图中新旧2组子节点的顺序没变化，图中也标注了旧的子节点的索引。

• key为1的节点，在旧children数组中索引为0
• key为2的节点，在旧children数组中索引为1
• key为3的节点，在旧children数组中索引为2

新子节点找在旧子节点中找到可以复用的元素，这些复用节点在旧的一组子节点中的位置索引可以得到一个序列： 0 1 2，这是一个递增的序列，这种情况下不需要移动任何节点。
然后按照上节的更新，调整新节点的位置，结果如下图显示

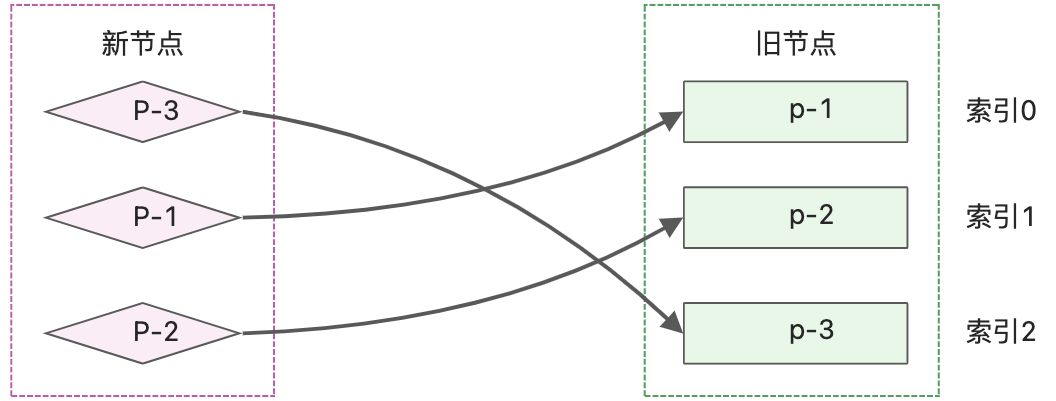
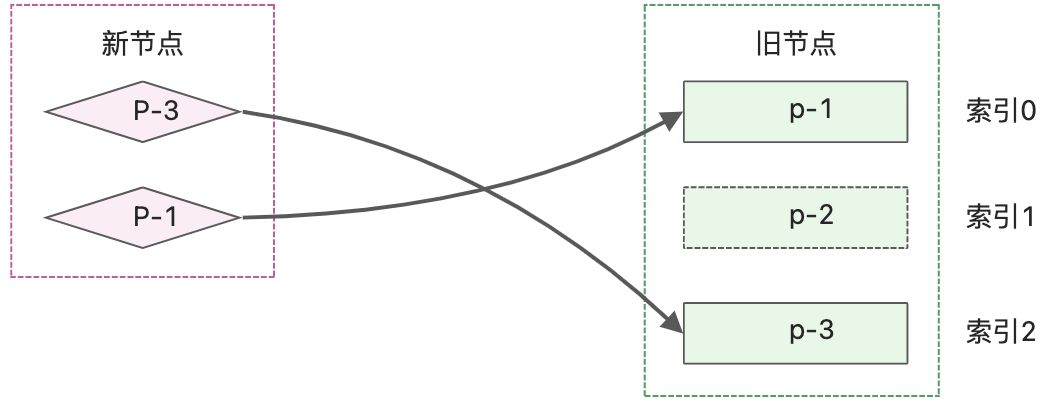
• 新子节点的第一个节点为p-3，它的key为3，在旧的子节点中可以查找到相同的key，说明可以复用，该节点在旧的子节点中的索引值为2.
• 新子节点的第二个节点为p-1，它的key为1，可以在旧的子节点中找到对应key，可以复用，索引为0；
• 新子节点的第二个节点为p-2，它的key为2，可以在旧的子节点中找到对应key，可以复用，索引为1；

这时可以发现索引值递增的顺序被打乱了，现在的序列为2、0、1；新p-1节点对应的索引小于新p-3节点对应的索引，【索引小本来应排在前】但是排在p-3的后边，说明p-1节点需要移动。同理，p-2节点的索引也小于p-3节点的索引，但仍排在后边，说明p-2节点需要移动。

在旧的children中查找具有相同key值节点的过程中，遇到的最大索引值，如果后续寻找的过程中，存在索引值比当前遇到的最大索引值还要小的节点，说明该节点需要移动。

可以使用lastIndex变量存储整个寻找过程中遇到的最大索引值。

function patchChildren(n1, n2, container) {
  if (typeof n2.children === 'string') {
    // ...
  } else if (Array.isArray(n2.children)) {
    const oldChildren = n1.children
    const newChildren = n2.children

    // 用lastIndex存储寻找过程中遇到的最大索引值
    let lastIndex = 0;
    for (let i = 0; i < newChildren.length; i++) {
      const newVNode = newChildren[i]
      let j = 0
      // 遍历旧的 children
      for (j; j < oldChildren.length; j++) {
        const oldVNode = oldChildren[j]
        // 如果找到了具有相同 key 值的两个节点，则调用 `patch` 函数更新
        // 节点相同，内容或属性可能已经发生变化
        if (newVNode.key === oldVNode.key) {
          patch(oldVNode, newVNode, container)
          if(j < lastIndex){
            // 如果当前找到的可复用节点，在旧的children中的索引小于最大索引值lastIndex
            // 说明该节点需要移动，怎么移动，下节在分析
          }else{
            // 如果当前找到的节点，在旧children中的索引 不小于 最大索引值，则更新lastINdex
            lastIndex = j;
          }
          break // 这里需要 break
        }
      }
    }
    
  } else {
    // ...
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

• 代码第18行，如果新节子节点的key相同，说明在旧的children中找到了可以复用的DOM节点
• 用可复用的节点在旧的children中的索引j与lastIndex进行比较，如果j小于lastIndex，说明节点需要移动。否则不需要移动，不移动的同时要将该变量j的值赋值给变量lastIndex，保证lastIndex始终存储着当前遇到的最大索引值。

示例代码

9.4 如何移动元素

上节找到了需要移动的节点元素p-1和p-2，接下来就要移动他们。移动节点指的是移动虚拟节点对应的真实DOM节点。要移动真实的DOM节点，就需要获取到对它的引用。真实DOM节点都是保存在虚拟节点的vnode.el属性中
在更新操作时，渲染器会调用patchElement函数在新旧虚拟节点之间进行打补丁。

function patchElement(n1, n2){
  // 新的vnode n2 引用了真实的DOM元素
  const el = n2.el = n1.el;
  // ...
}
1
2
3
4
5

patchElement函数首先将旧节点的n1.el属性赋值给新节点的n2.el属性，其实就是DOM元素的复用。复用之后，新节点也将持有对真实DOM的引用。
添加上新节节点之间的关系

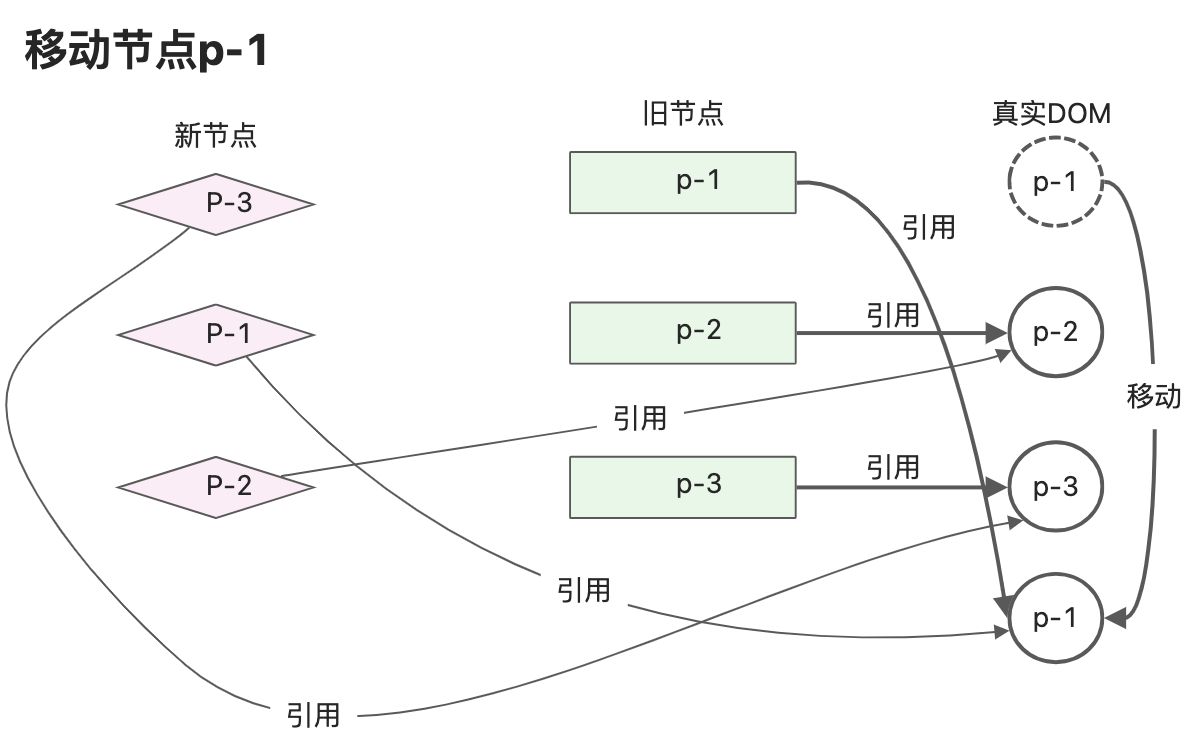
更新步骤如下：

• 新子节点的第一个节点p-3，key为3，通过遍历查询可以找到相同的key值，说明节点可以复用。并且该节点在旧的子节点中的索引为2，原lastIndex值为0，小于2，说明DOM节点不需要移动，并更新lastIndex值为2
• 新子节点的第二个节点p-1，key为1，从旧节点中查询出可以复用节点，并且该节点在旧的子节点中索引为0，此时lastIndex为2，索引0小于2，说明节点p-1需要移动。
  • 节点p-1对应的真实DOM需要移动。新children的顺序就是更新后真实DOM节点应该的顺序，所以p-1节点在新children的位置就代表了真实DOM更新后的位置。p-1节点排在p-3节点的后边，所以应该把p-1节点所对应的真实DOM移动到节点p-3所对应的真实DOM后面，移动后DOM顺序 p-2、p-3、p-1
• 新子节点的第三个阶段p-2，key为2，也是可以复用的节点，发现该节点在旧子节点中的索引为1，此时lastIndex的为为2，索引1小于2，所以节点p-2对应的真实DOM需要移动。
  • 节点p-2在新children中排在节点p-1后面，所以应该把p-2对应的真实DOM移动到p-1对应的真实DOM后。

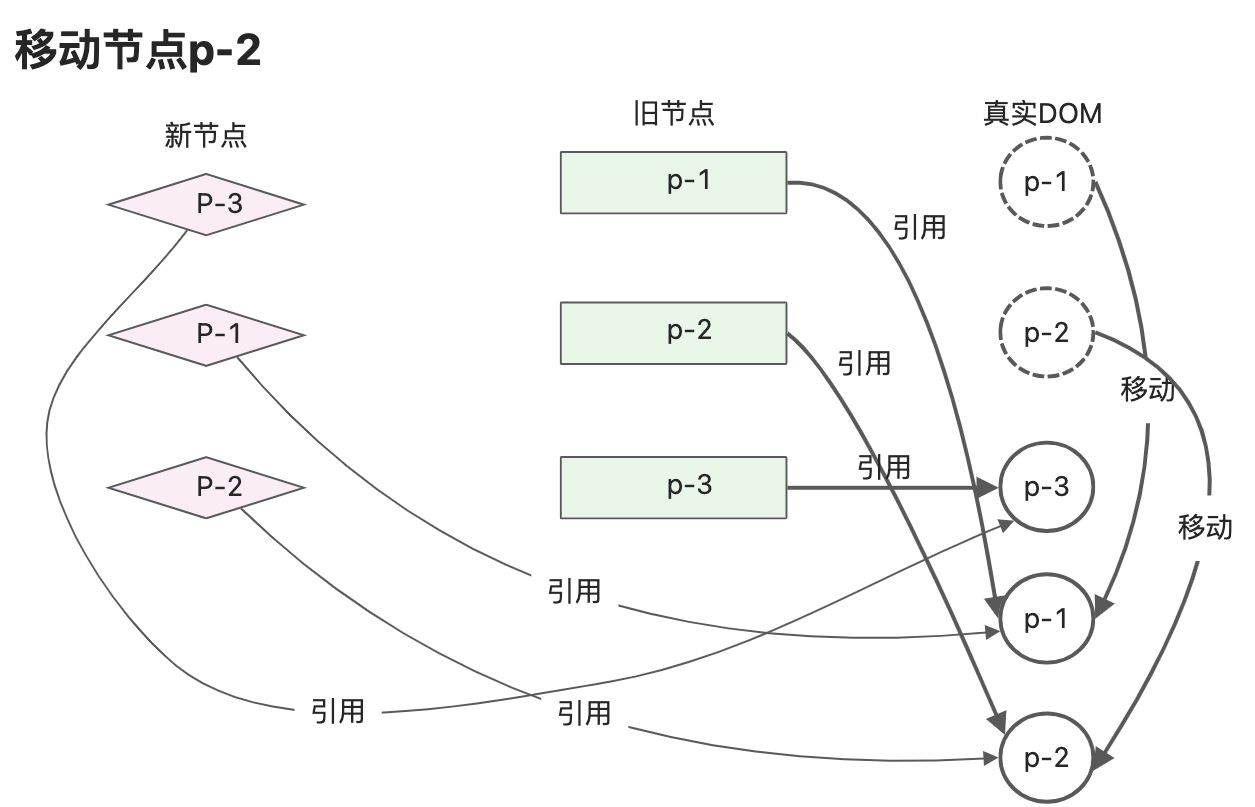
经过移动操作，此时真实DOM的顺序与新的一组子节点的顺序相同，p-3、p-1、p-2。
最后用代码实现移动的过程。

function patchChildren(n1, n2, children){
  if(typeof n2.children === "string"){
   //...
  }else if(Array.isArray(n2.children)){
    const oldChildren = n1.children;
    const newChildren = n2.children;
    let lastIndex = 0;
    for(let i=0; i<newChildren.length; i++){
      const newVnode = newChildren[i];
      let j=0;
      for(j; j< oldChildren.length; j++){
        const oldeVnode = oldChildren[j];
        if(newVnode.key === oldVnode.key){
          patch(oldVnode, newVnode, container);//先进行patch，然后在进行移动
          if(j<lastIndex){ //需要移动操作
            // 进入这个判断，说明newVnode对应的真实DOM需要移动
            // 先获取newVnode的前一个vnode，定义为preVnode
            const prevVnode = newChildren[i-1];
            // 如果prevVnode不存在，说明当前的newVnode是第一个节点，不需要移动
            if(prevVnode){
              // 将newVnode对应的真实DOM移动到prevVnode所对应的真实DOM后边
              // 需要获取prevVnode所对应真实DOM的下一个兄弟节点，并将其设为锚点
              cosnt anchor = prevVnode.el.nextSibling;
              // 调用insert方法，将newVnode对应的真实DOM 插入到锚点元素前面
              insert(newVnode.el, container, anchor);
            }
          }else{
            lastIndex = j;
          }
          break;
        }
      }
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

更新渲染器的参数方法，新增insert方法；insert函数依赖浏览器原生的insertBefore函数。

const renderer = createRenderer({
  // ...
  insert(el, parent, anchor=null){
    // insertBefore需要锚点元素 anchor
    parent.insertBefore(el, anchor);
  }
})
1
2
3
4
5
6
7

代码示例

9.5添加新元素

如果在新子节点元素中新增了节点，多个p-4，它的key为4，该节点在旧的子节点中不存在，所以在更新时应该正确的将它挂载，主要分为2步：

• 找到新增节点
• 将新增节点挂载到正确位置

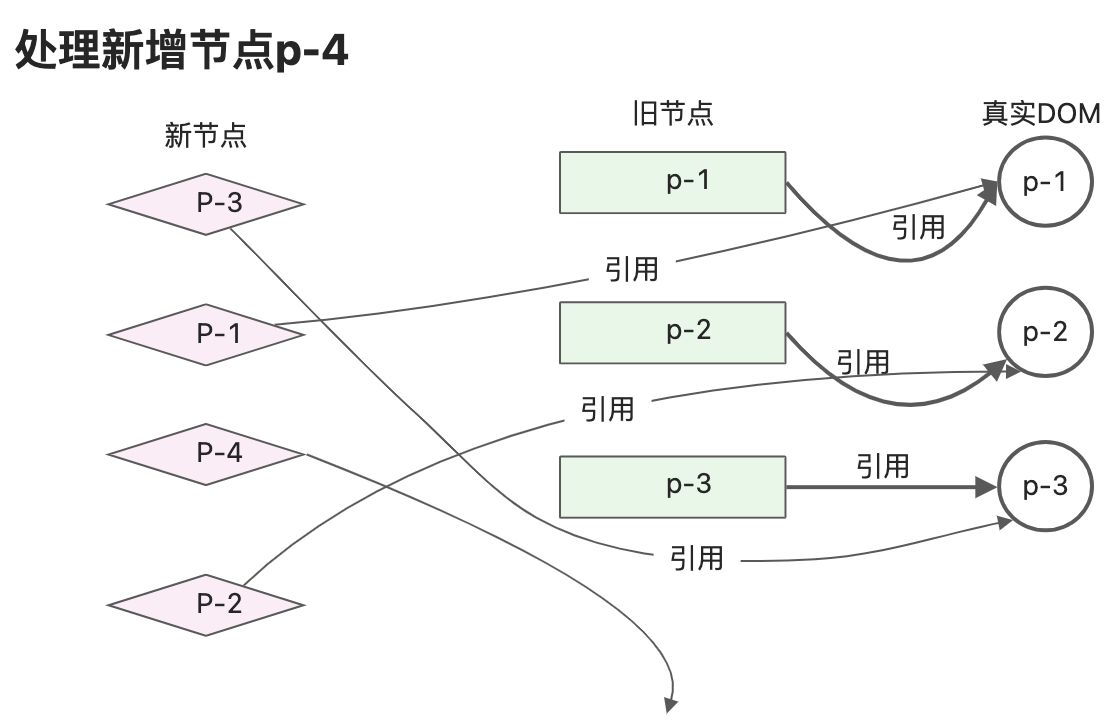
开始模拟执行简单的Diff算法：

• 新的子节点中第一个节点p-3，key为3，可以在旧的子节点中找到可复用节点，索引值为2。此时lastIndex的值为0，索引2不小于0，所以p-3不需要移动，需要将lastIndex的值更新为2；
• 新的子节点中第2个节点p-1，key为1，可以在旧的子节点中找到可复用节点，索引值为0。此时lastIndex的值为2，索引0小于2，所以p-1需要移动，将节点p-1移动到p-3后边，经过这步的移动，此时真实DOM顺序为p-2、p-3、p-1；

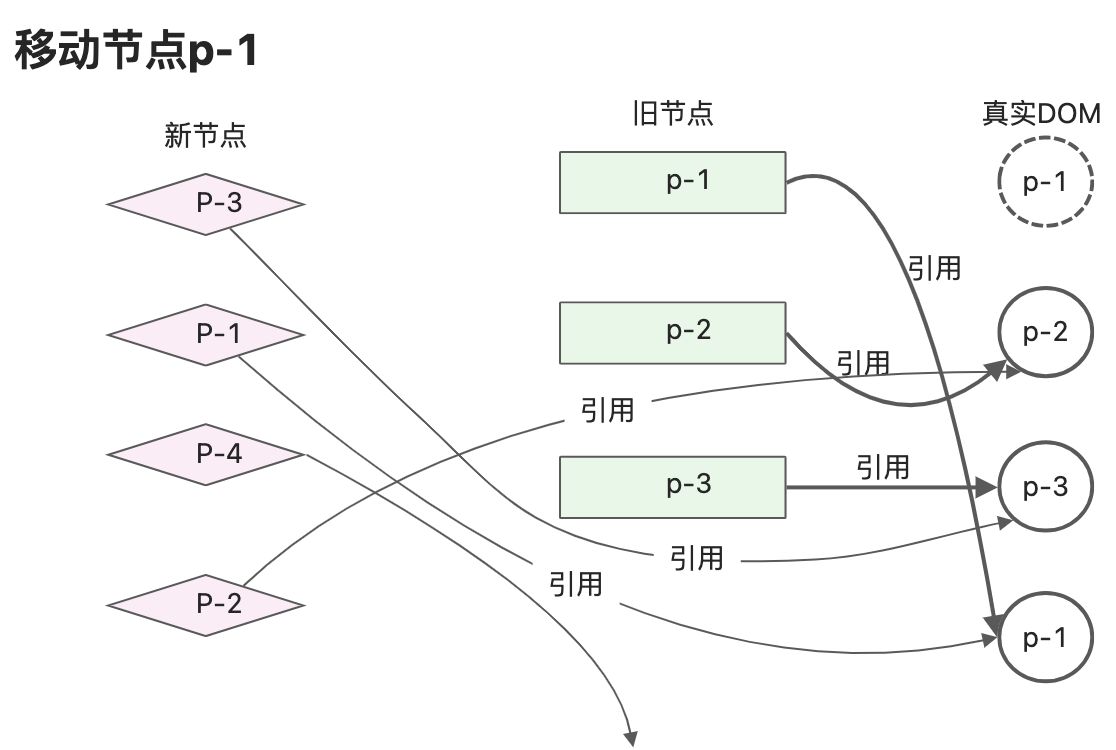
• 新的子节点中的第3个节点p-4，它的key为4，尝试在旧子节点中查询该节点，找不到可复用的节点，因此渲染器会把p-4看作新增节点并挂载它。节点p-4在新的一组子节点中的位置在p-1后边，所以应该把节点p-4挂载到p-1对应的真实DOM后边。 此时真实DOM顺序为p-2、p-3、p-1、p-4。

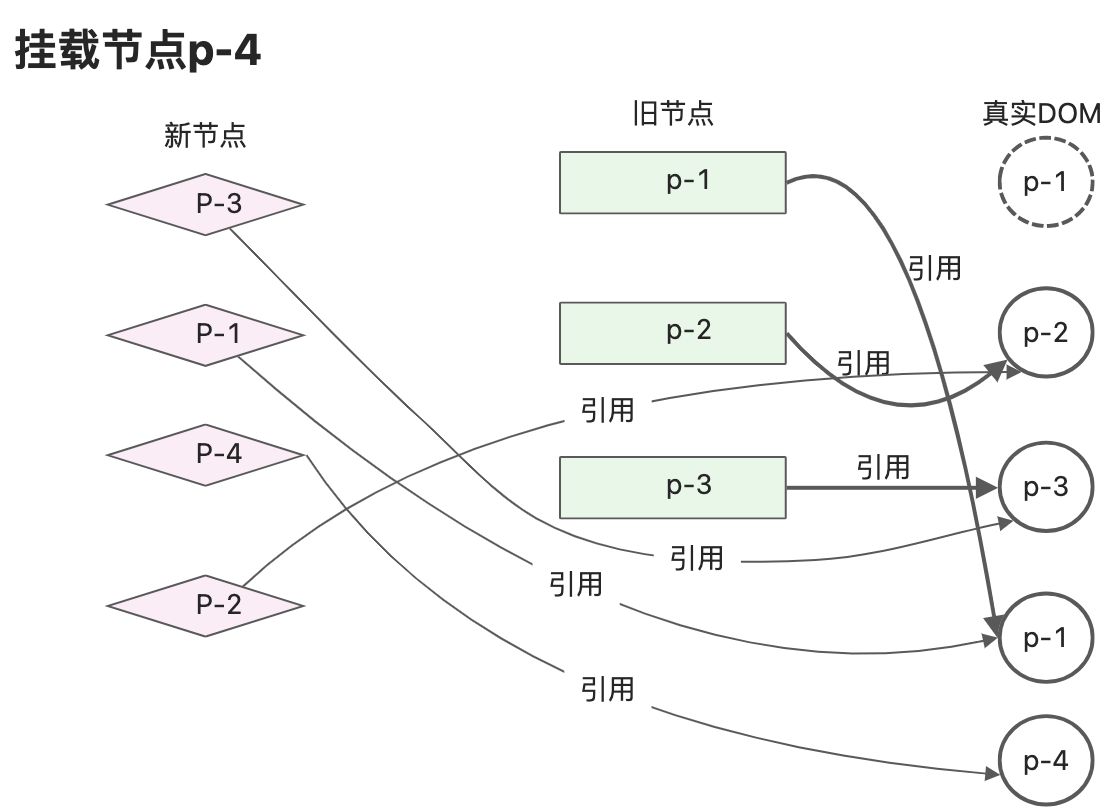
• 新的子节点中第4个节点p-2，key为2，可以在旧的子节点中找到可复用节点，索引值为1。此时lastIndex的值为2，索引1小于2，所以p-2需要移动，将节点p-2移动到p-1后边，经过这步的移动，此时真实DOM顺序为p-3、p-1、p-4、p-2；至此真实DOM顺序已经和新的一组子节点顺序相同。

接下来通过代码实现节点的移动和挂载。
在外层循环中定义了名为find的变量，代表渲染器能否在旧的一组子节点中找到可复用的节点。find的初始值为false，一旦找到可复用节点，find更新为true。如果内层循环结束后，find变量仍为false时，说明newVnode是全新的节点，需要挂载它，为了将节点挂载到正确的位置，需要先获取锚点元素，找到newVnode的前一个虚拟节点，即prevVnode。如果存在，则使用它对应的真实DOM的下一个兄弟节点作为锚点元素，如果不存在，则说明将挂载的newVnode节点是容器元素的第一个子节点，此时使用容器元素的container.firstChild作为锚点元素。最后将锚点元素anchor作为patch函数的第4个参数，调用patch函数完成节点的挂载。

function patchChildren(n1, n2, container) {
    if (typeof n2.children === 'string') {
      //...
    } else if (Array.isArray(n2.children)) {
      const oldChildren = n1.children
      const newChildren = n2.children

      let lastIndex = 0
      // 遍历新的 children
      for (let i = 0; i < newChildren.length; i++) {
        const newVNode = newChildren[i]
        let j = 0
        let find = false
        // 遍历旧的 children
        for (j; j < oldChildren.length; j++) {
          const oldVNode = oldChildren[j]
          // 如果找到了具有相同 key 值的两个节点，则调用 `patch` 函数更新
          if (newVNode.key === oldVNode.key) {
            find = true
            patch(oldVNode, newVNode, container)
            if (j < lastIndex) {
              // 需要移动
              const prevVNode = newChildren[i - 1]
              if (prevVNode) {
                const anchor = prevVNode.el.nextSibling
                insert(newVNode.el, container, anchor)
              }
            } else {
              // 更新 lastIndex
              lastIndex = j
            }
            break // 这里需要 break
          }
        }
        // 在旧子节点中未找到，说明是新增的节点
        if (!find) {
          //为了将节点挂载到正确位置，需要先获取锚点元素。
          // 首先获取当前newVnode的前一个vnode节点。
          const prevVNode = newChildren[i - 1]
          let anchor = null
          if (prevVNode) {
            // 如果有前一个vnode节点，则使用它的下一个兄弟节点作为锚点元素。
            anchor = prevVNode.el.nextSibling
          } else {
            // 如果没有前一个vnode节点，说明即将挂载的新节点是第一个子节点
            // 需要使用容器元素 container.firstChild作为锚点
            anchor = container.firstChild
          }
          patch(null, newVNode, container, anchor)
        }
      }
      
    } else {
      // ...
    }
  }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

更新patch函数，。让其支持第4个参数。

function patch(n1, n2, container, anchor) {
  if (n1 && n1.type !== n2.type) {
    unmount(n1)
    n1 = null
  }

  const { type } = n2

  if (typeof type === 'string') {
    if (!n1) {
      mountElement(n2, container, anchor)
    } else {
      patchElement(n1, n2)
    }
  } else if (type === Text) {
    if (!n1) {
      const el = n2.el = createText(n2.children)
      insert(el, container)
    } else {
      const el = n2.el = n1.el
      if (n2.children !== n1.children) {
        setText(el, n2.children)
      }
    }
  } else if (type === Fragment) {
    if (!n1) {
      n2.children.forEach(c => patch(null, c, container))
    } else {
      patchChildren(n1, n2, container)
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

代码示例

9.6删除元素

更新子节点时，不仅会遇到新增元素，还会出现元素删除的情况。

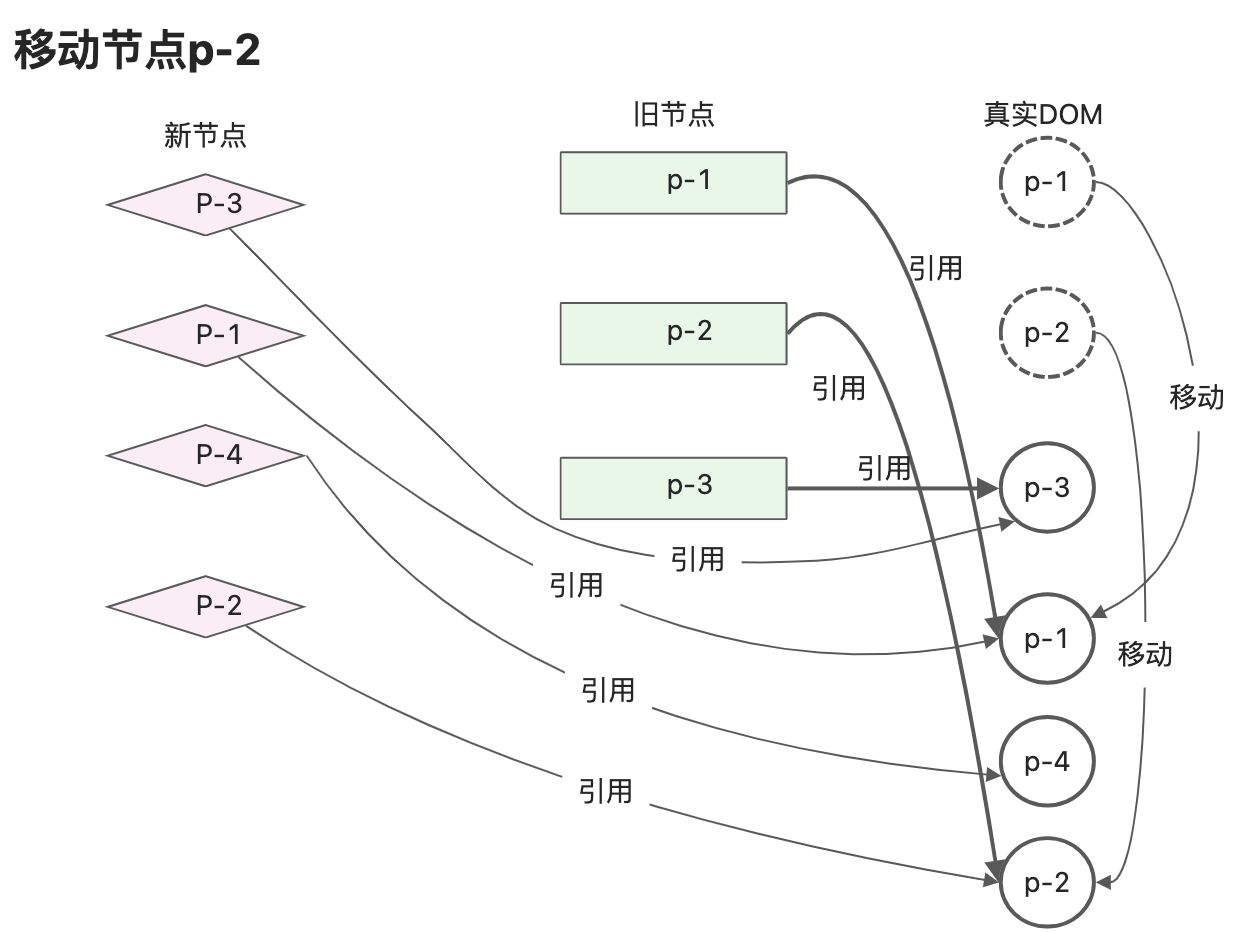
在新的一组子节点中p-2节点已经不存在，说明该节点被删除。
模拟渲染器执行更新的过程

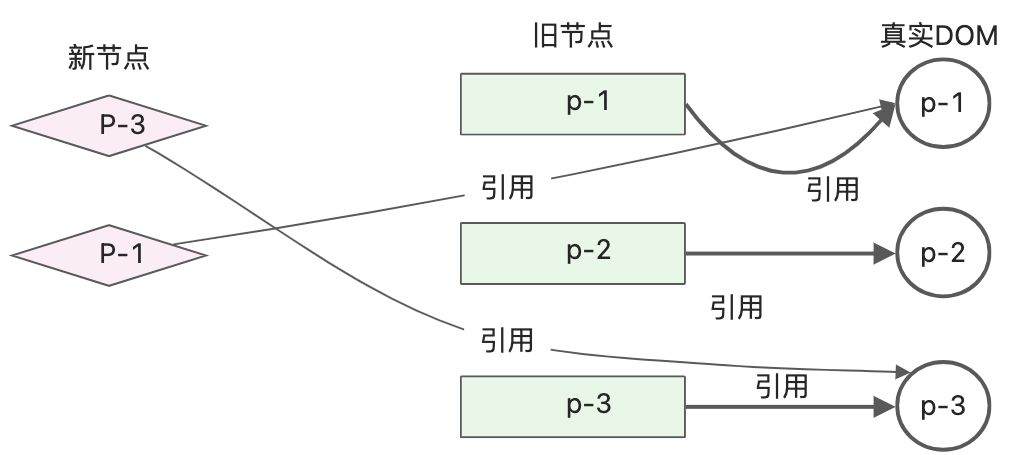
• 新的子节点中第一个节点p-3，key为3，可以在旧的子节点中找到可复用节点，索引值为2。此时lastIndex的值为0，索引2不小于0，所以p-3不需要移动，需要将lastIndex的值更新为2；
• 新的子节点中第2个节点p-1，key为1，可以在旧的子节点中找到可复用节点，索引值为0。此时lastIndex的值为2，索引0小于2，所以p-1需要移动，将节点p-1移动到p-3后边，经过这步的移动，此时真实DOM顺序为p-2、p-3、p-1；

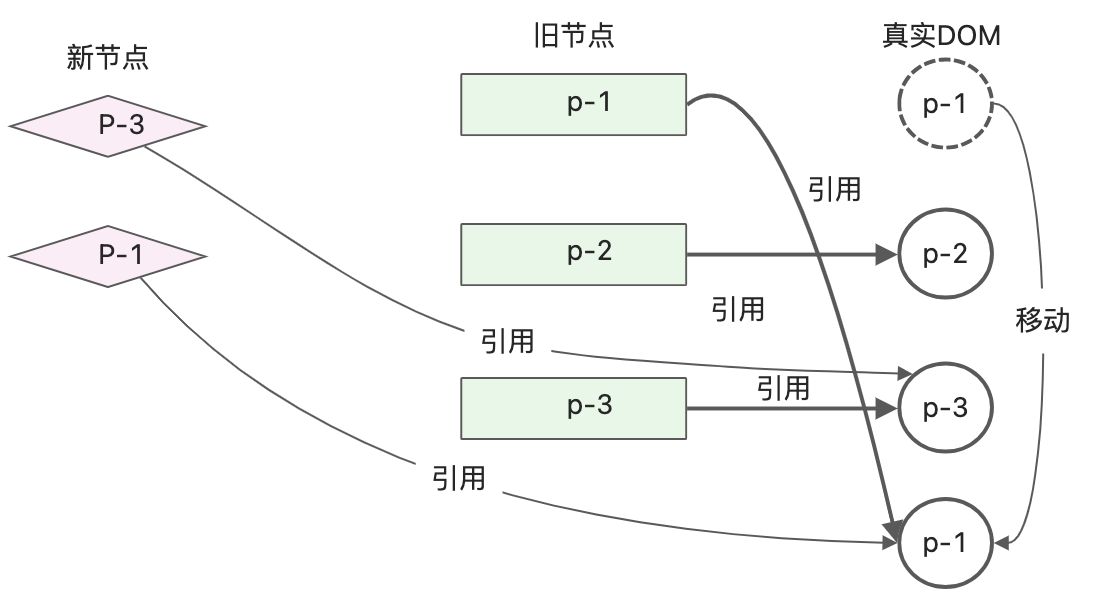
此时已经更新结束，但是可以发现旧子节点中p-2仍然存在，所以需要增加额外的逻辑来删除遗留的节点。
当基本更新结束后，需要遍历一遍旧的子节点，然后去新的一组子节点中寻找具有相同key值的节点。如果找不到，则说明需要删除该节点。更新patchChild函数

function patchChildren(n1, n2, container){
  if(typeof n2.children === "string"){
   //...
  }else if(Array.isArray(n2.children)){
    const oldChildren = n1.children;
    const newChildren = n2.children;
    let lastIndex= 0;
    for(let i = 0; i<newChildren.length; i++){
     //..
    }
    //遍历旧的一组子节点
    for(let i=0;i<oldChildren.length; i++){
      const oldVnode = oldChildren[i];
      // 用旧子节点 oldVnode去新的一组子节点中寻找具有相同key值的节点
      const has = newChildren.find(vnode => vnode.key === oldVnode.key);
      // 	如果新的子节点中不存在
      if(!has){
        // 在新的子节点中不存在，说明需要删除该节点，调用unmount函数将节点卸载
        unmount(oldVnode);
      }
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

代码示例

10.双端Diff算法(vue2)

简单的diff算法，使用了双层for循环，在计算数据量大的情况下，无法应用到项目中。该算法还存在很多缺陷。

10.1双端比较的原理

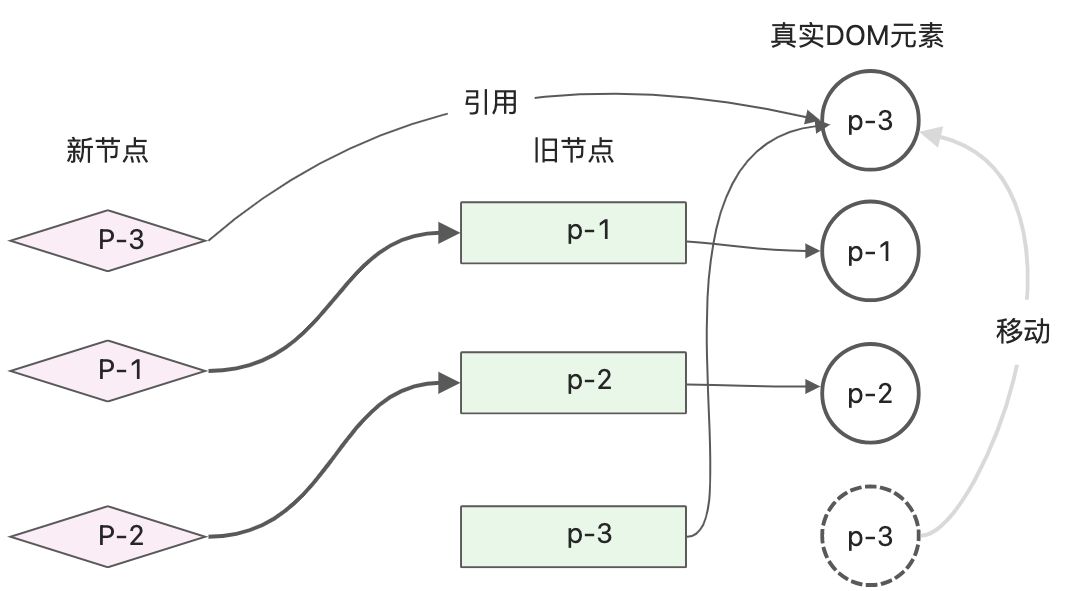
简单的diff算法问题在于，它对DOM的移动操作不是最优的。

上面节点变动，按照简单diff算法需要移动2次DOM，是不是还可以继续优化，只需要移动一次呢。其实可以只需要把真实DOM节点p-3移动到真实DOM节点p-1前面即可。

可以看到只需一次移动操作就可完成更新，但是简单的diff算法还做不到。接下来实现双端diff算法的原理。

双端diff算法是一种同时对新旧两组子节点的2个端点进行比较的算法。
需要4个索引值，分别指向新旧2组子节点的端点。

用代码来表示4个端点

function patchChildren(n1, n2, container){
  if(typeof n2.children === "string"){
   //...
  }else if(Array.isArray(n2.children)){
    // 封装patchKeyedChildren函数 处理两组子节点
    patchKeyedChildren(n1, n2, children)
  }else{
   //...
  }
}
function patchKeyedChildren(n1, n2, children){
  const oldChildren = n1.children;
  const newChildren =n2.children;
  // 4个索引
  let oldStartIndex = 0;
  let oldEndIndex = oldChildren.length -1;
  let newStartIndex = 0;
  let newEndIndex = newChildren.length -1;
  // 4个索引指向的vnode节点
  let oldStartVnode = oldChildren[oldStartIndex];
  let oldEndVnode = oldChildren[oldEndIndex];
  let newStartVnode = newChildren[newStartIndex];
  let newEndVnode = newChildren[newEndIndex];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

• oldStartVnode和oldEndVnode是旧的一组子节点的第一个节点和最后一个节点
• newStartVnode和newEndVnode是新的一组子节点的第一个节点和最后一个节点

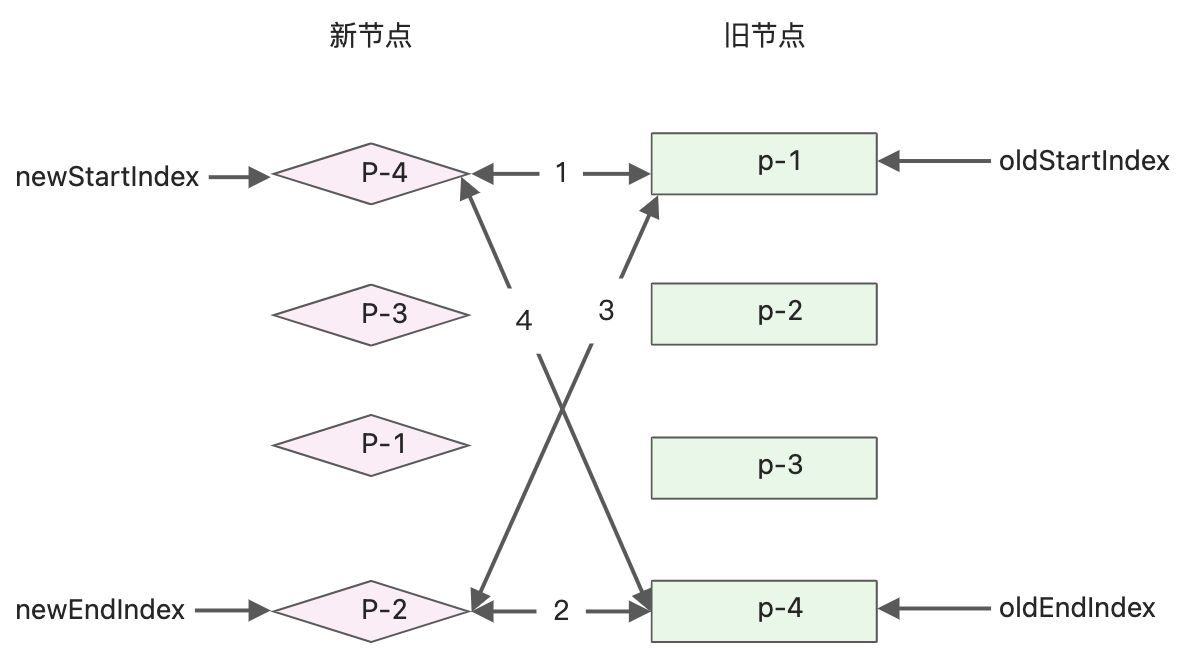
双端比较中，每一轮都分为4个步骤进行比较。头头、尾尾、头尾、尾头

• 比较旧节点的第一个子节点p-1与新的一组子节点中的第一个子节点p-4，看他们是否相同，由于key不同，因此不可复用。什么都不做，继续下面的操作
• 比较旧节点的最后一个子节点p-4与新的一组子节点的最后一个子节点p-2，两者key不同，不可复用，继续后边操作。
• 比较旧节点的第一个子节点p-1与新的一组子节点中最后一个子节点p-2，两个key不同，不可复用。
• 比较旧节点的最后一个子节点p-4与新的一组子节点的第一个节点p-4，key相同，可以进行DOM复用

可以看到在四步比较过程中，第四步是比较旧的一组子节点的最后一个子节点和新的一组子节点的第一个子节点，发现他们相同。说明节点p-4原本是最后一个子节点，但在新顺序中，它变成了第一个子节点。对应的程序逻辑：将索引oldEndIndex指向的虚拟节点所对应的真实DOM移动到索引oldStartIndex指向的虚拟节点所对应的真实DOM前面。

function patchKeyedChildren(n1, n2, children){
  const oldChildren = n1.children;
  const newChildren =n2.children;
  // 4个索引
  let oldStartIndex = 0;
  let oldEndIndex = oldChildren.length -1;
  let newStartIndex = 0;
  let newEndIndex = newChildren.length -1;
  // 4个索引指向的vnode节点
  let oldStartVnode = oldChildren[oldStartIndex];
  let oldEndVnode = oldChildren[oldEndIndex];
  let newStartVnode = newChildren[newStartIndex];
  let newEndVnode = newChildren[newEndIndex];
  
  if(oldStartVnode.key === newStartVnode.key){ // 头头
    // 第一步：oldStartVnode 和 newStartVnode比较
  }else if(oldEndVnode.key === newEndVnode.key){ // 尾尾
    // 第二步：oldEndVnode 和 newEndVnode
  }else if(oldStartVnode.key === newEndVnode.key){ //头尾
    // 第三步：oldStartVnode 和 newEndVnode
  }else if(oldEndVnode.key === newStartVnode.key){ // 尾头
    // 第四步：oldEndVnode 和 newStartVnode
    //使用patch函数进行打补丁
    patch(oldEndVnode, newStartVnode, container);
    // 移动DOM操作
    // oldEndVnode.el 移动到 oldStartVnode.el前面
    insert(oldEndVnode.el, container, oldStartVnode.el)
    
    // 移动DOM完成后，更新索引值，并指向下一个位置
    oldEndVnode = oldChildren[--oldEndIndex];
    newStartVnode = newChildren[++newStartIndex];
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

代码中增加了一系列if…else if…判断用来实现四个索引指向的虚拟节点之间的比较。就拿第四步的比较来说，原来处于尾部的节点，在新的顺序中应该处于头部。于是以头部元素oldStartVnode.el作为锚点，将尾部元素的oldEndVnode.el移动到锚点前。在进行DOM移动之前，仍需要调用patch函数在新旧虚拟节点之间打补丁。
DOM移动后，需要更新对应的索引值，第四步涉及的2个索引为oldEndIndex 和newStartIndex

经过第一遍的对比，执行过第四步的操作。此时新旧两组子节点及真实DOM节点的状态

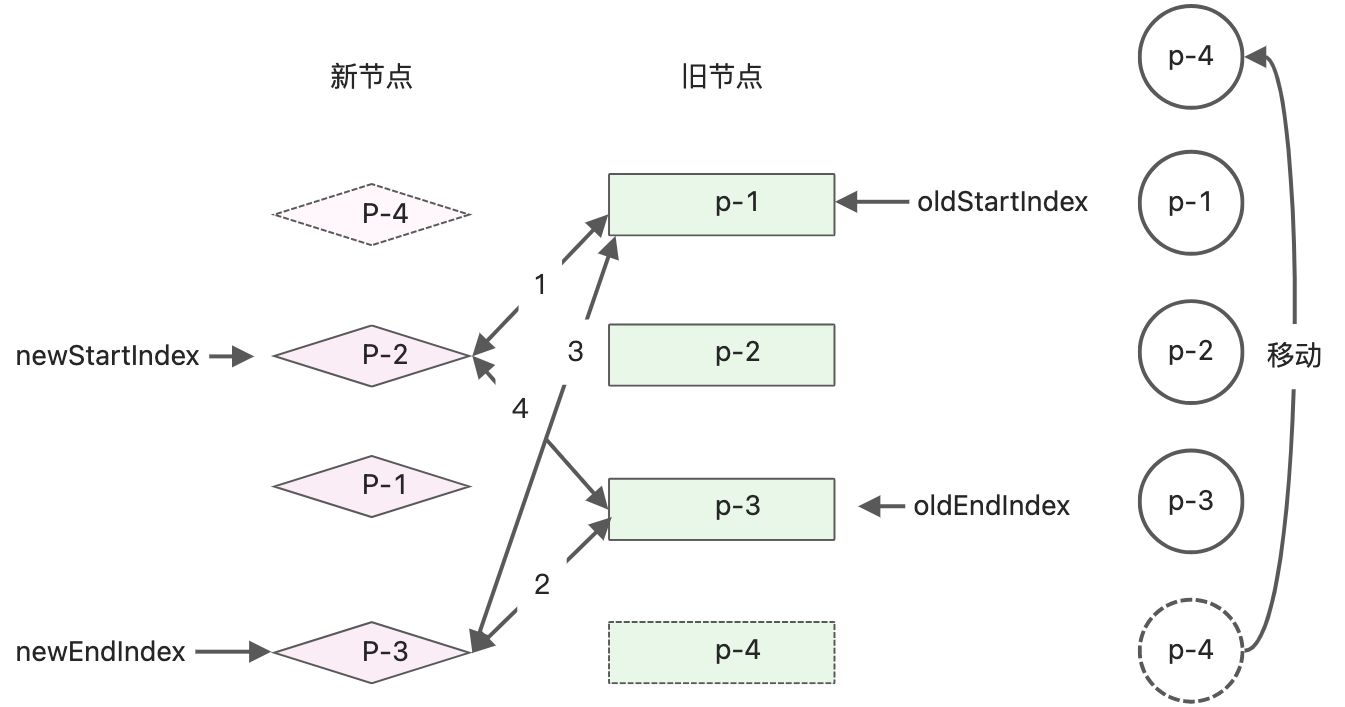
此时真实DOM节点的顺序为p-4、p-1、p-2、p-3。
开启下一轮的Diff算法更新。因此需要将4个对比的逻辑封装到while循环中,while循环的执行条件是：头部索引值小于等于尾部索引值。

while(oldStartIndex <= oldEndIndex && newStartIndex <= newEndIndex){
  if(oldStartVnode.key === newStartVnode.key){
    // oldStartIndex 和 newStartIndex对比
  }else if(oldEndVnode.key === newEndVnode.key){
    // oldEndIndex 和 newEndIndex对比
    // 旧的尾部p-3 和 新的尾部p-3相同，进入这个判断条件
    // 给oldEndVnode newEndVnode节点进行打补丁操作
    patch(oldEndVnode, newEndVnode, container);
    // 更新索引值
    oldEndVnode = oldChildren[--oldEndIndex];
    newEndVnode = newChildren[--newEndIndex];
  }else if(oldStartVnode.key === newEndVnode.key){
    // oldStartIndex 和 newEndIndex 对比
  }else if(oldEndVnode.key === newStartVnode.key){
    // oldEndIndex 和 newStartIndex 对比
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

真实DOM的顺序没有发生变动，只是对p-3节点进行打补丁操作。
更新完整后，新旧两组子节点与真实DOM的节点状态

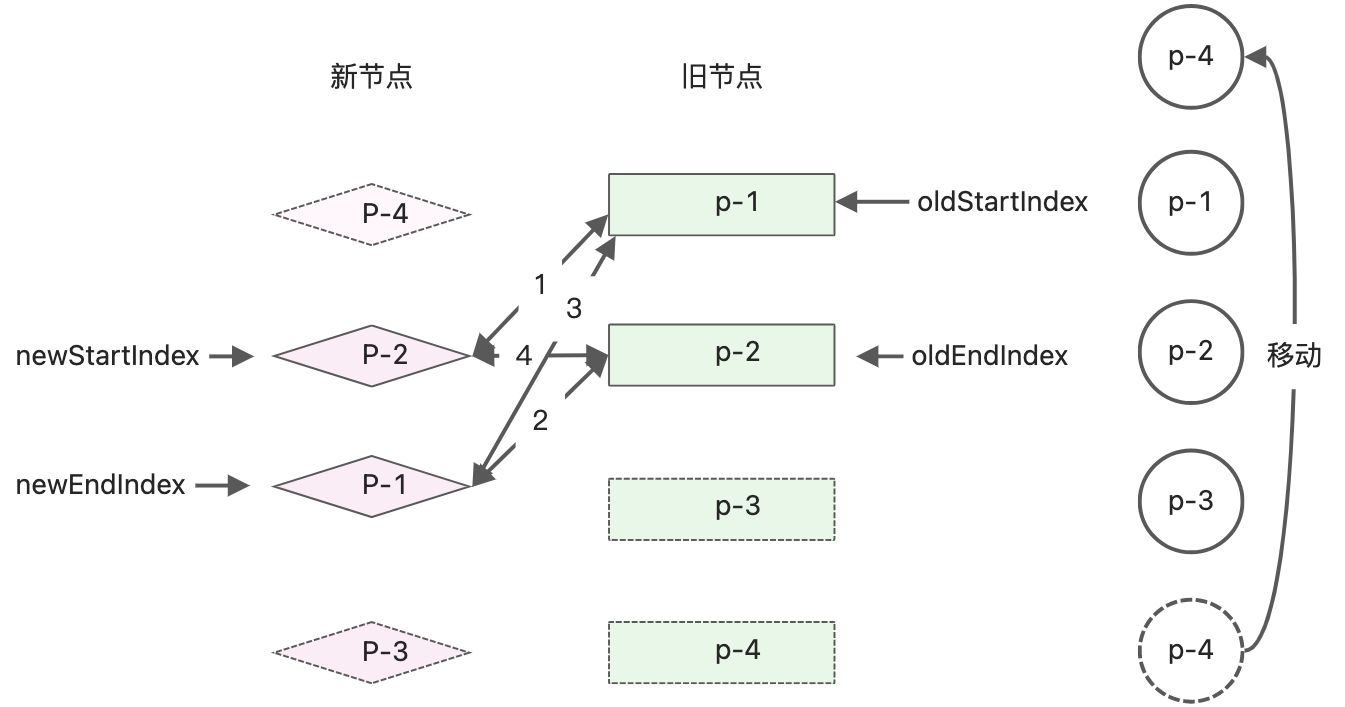
接下来进行下一轮的Diff更新

• 头头对比，key不相同，进行下个if判断
• 尾尾对比，key不相同，进行下个if判断
• 头尾对比，p-1的key相同，进入对比。旧节点头部p-1，在新节点中变成了尾部。需要将p-1的真实DOM移动到旧子节点的尾部节点p-2所对应的真实DOM后边。同时更新对应的索引到下一个位置。

while(oldStartIndex <= oldEndIndex && newStartIndex <= newEndIndex){
  if(oldStartVnode.key === newStartVnode.key){
    // oldStartIndex 和 newStartIndex对比
  }else if(oldEndVnode.key === newEndVnode.key){
    // oldEndIndex 和 newEndIndex对比
  }else if(oldStartVnode.key === newEndVnode.key){
    // oldStartIndex 和 newEndIndex 对比
    // 旧的头部p-1 和 新的尾部p-1相同，进入这个判断条件
    // oldStartVnode newEndVnode节点进行打补丁操作
    patch(oldStartVnode, newEndVnode, container);
    // 将旧头部节点对于的dom oldStartVnode.el 移动到旧尾部节点对应的DOM节点后边
    insert(oldStartVnode.el, container, oldEndVnode.el.nextSibling);
    // 更新索引值
    oldStartVnode = oldChildren[++oldEndIndex];
    newEndVnode = newChildren[--newEndIndex];
  }else if(oldEndVnode.key === newStartVnode.key){
    // oldEndIndex 和 newStartIndex 对比
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

移动p-1节点对应的真实DOM，更新索引值。之后的新旧节点和真实DOM的状态如下图

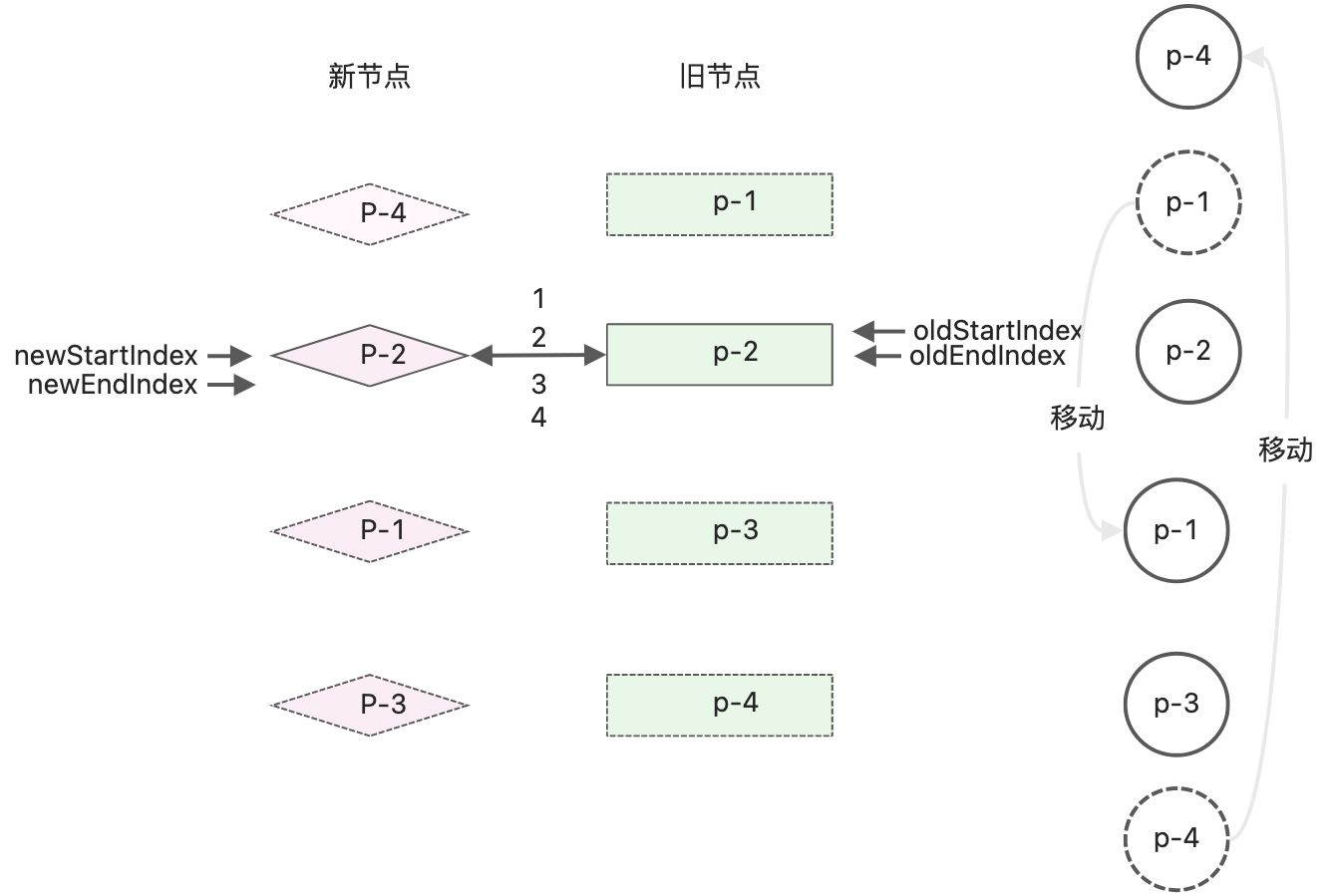
此时，新旧两组子节点的头部索引和尾部索引发生重合，还是满足while的条件，继续进行下轮的diff更新。

• 比较旧的一组子节点中的头部节点p-2与新的一组子节点的头部节点p-2，发现key值相同，可以复用，不用移动DOM，只需patch函数进行打补丁。

while(oldStartIndex <= oldEndIndex && newStartIndex <= newEndIndex){
  if(oldStartVnode.key === newStartVnode.key){
    // oldStartIndex 和 newStartIndex对比
    // 进入判断条件 p-2节点的对比，调用patch函数，对oldStartVnode和newStartVnode打补丁
    patch(oldStartVnode, newStartVnode, container);
    // 更新相关索引，指向下一个位置
    oldStartVnode  = oldChildren[++oldStartIndex];
    newStartVnode = newChildren[++newStartIndex];
  }else if(oldEndVnode.key === newEndVnode.key){
    // oldEndIndex 和 newEndIndex对比
  }else if(oldStartVnode.key === newEndVnode.key){
    // oldStartIndex 和 newEndIndex 对比
    // 旧的头部p-1 和 新的尾部p-1相同，进入这个判断条件
    // oldStartVnode newEndVnode节点进行打补丁操作
    patch(oldStartVnode, newEndVnode, container);
    // 将旧头部节点对于的dom oldStartVnode.el 移动到旧尾部节点对应的DOM节点后边
    insert(oldStartVnode.el, container, oldEndVnode.el.nextSibling);
    // 更新索引值
    oldStartVnode = oldChildren[++oldEndIndex];
    newEndVnode = newChildren[--newEndIndex];
  }else if(oldEndVnode.key === newStartVnode.key){
    // oldEndIndex 和 newStartIndex 对比
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

经过这轮的更新，及索引值的更新，新旧节点和真实DOM节点的状态，如下图

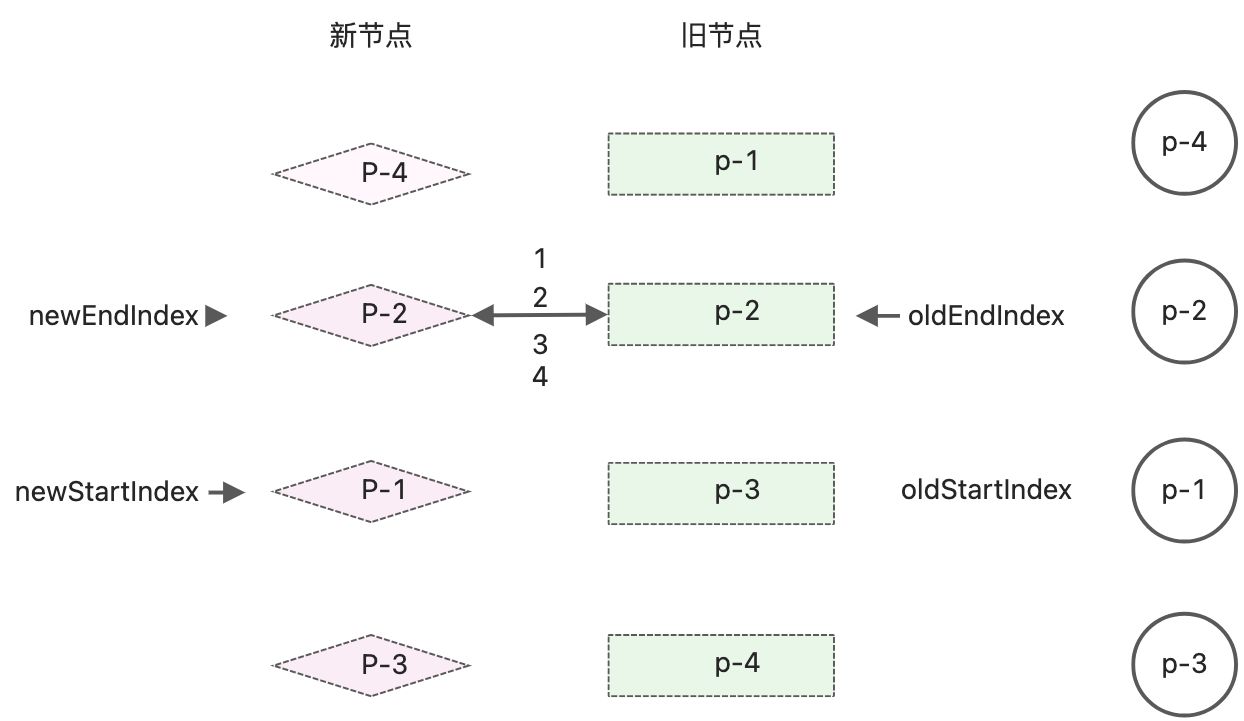
真实DOm节点顺序和新的子节点顺序相同：p-4、p-2、p-1、p-3。这轮更新完后，索引也更新后，发生了oldStartIndex和newStartIndex都小于oldEndIndex和newEndIndex的值，while循环终止，双端diff算法执行完毕
代码示例

10.2双端比较的优势

对比简单diff和双端diff的算法，完成如下图的变动

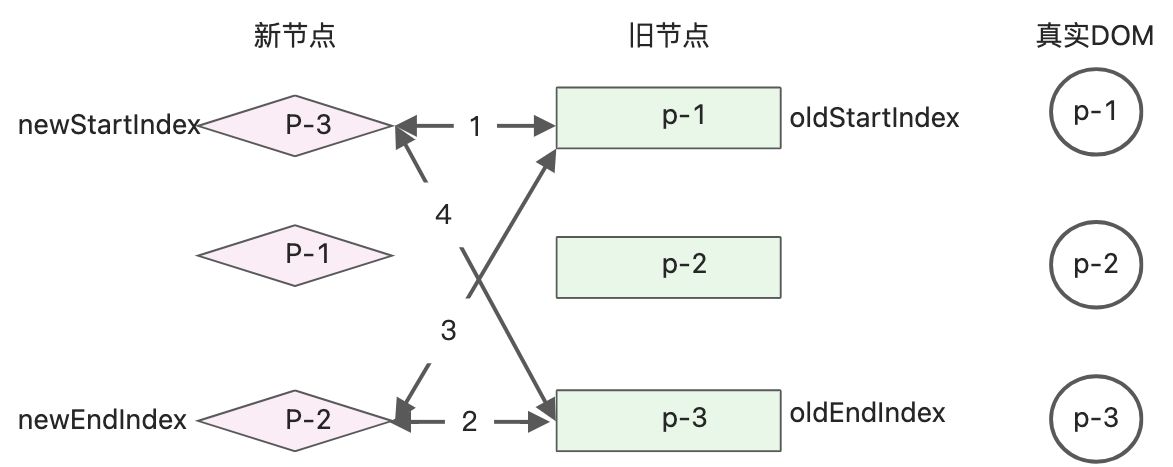
在简单diff算法中，需要比对vnode并移动DOM各3次，在双端Diff中，只需要一次DOM移动，进行3次patch操作就可以完成。
可见双端diff对减少DOM移动是非常有利。

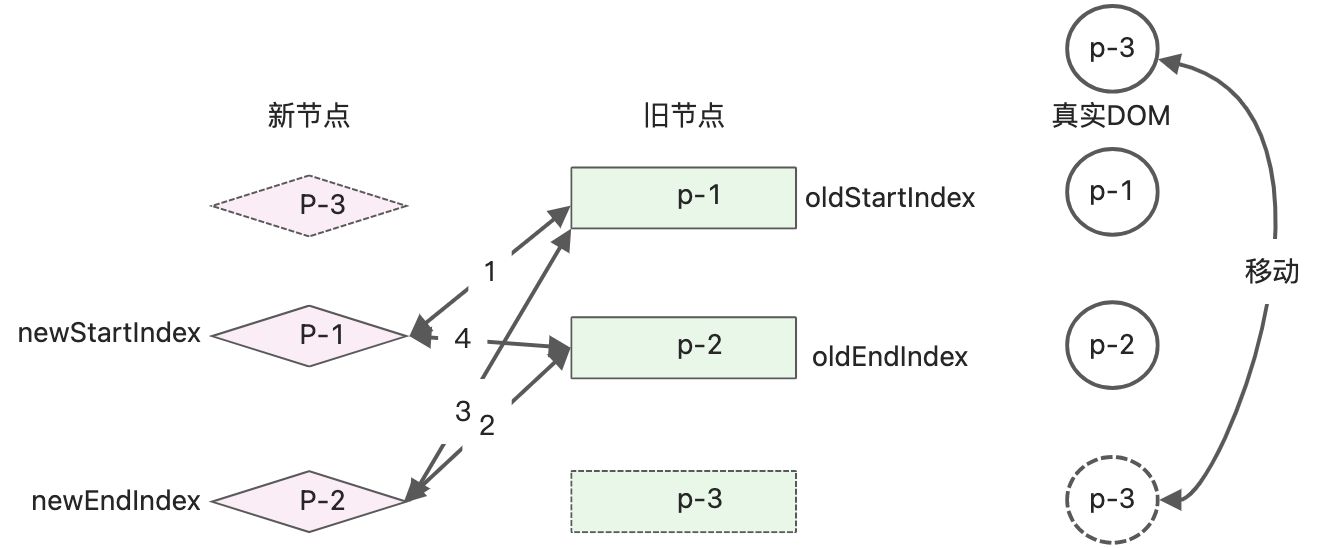
继续进行while的判断，diff算法更新


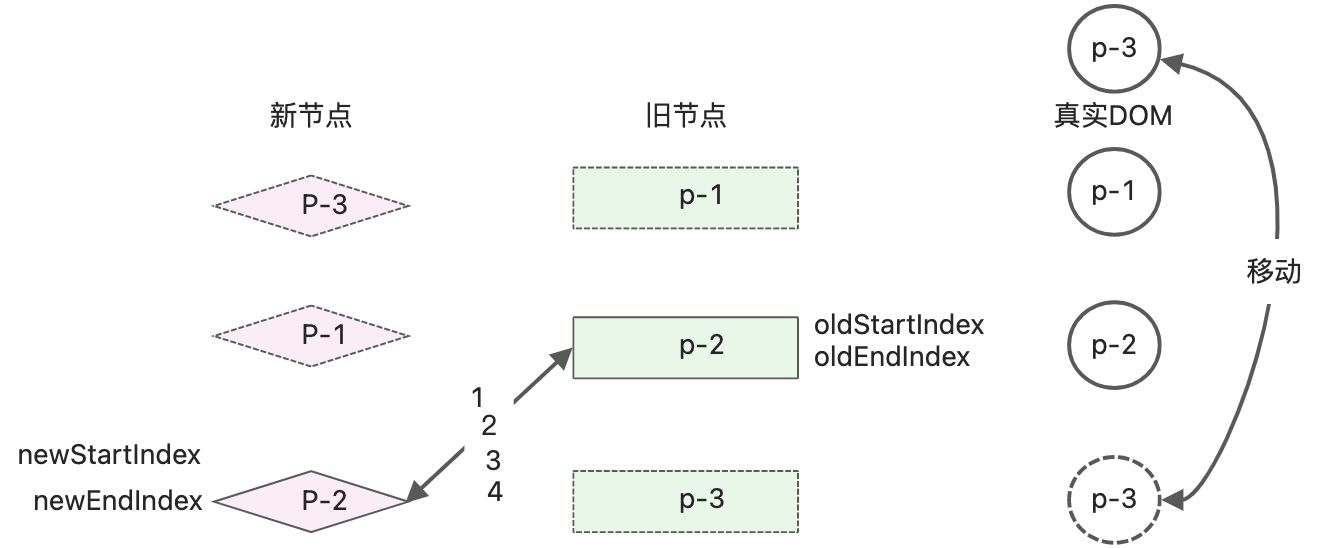
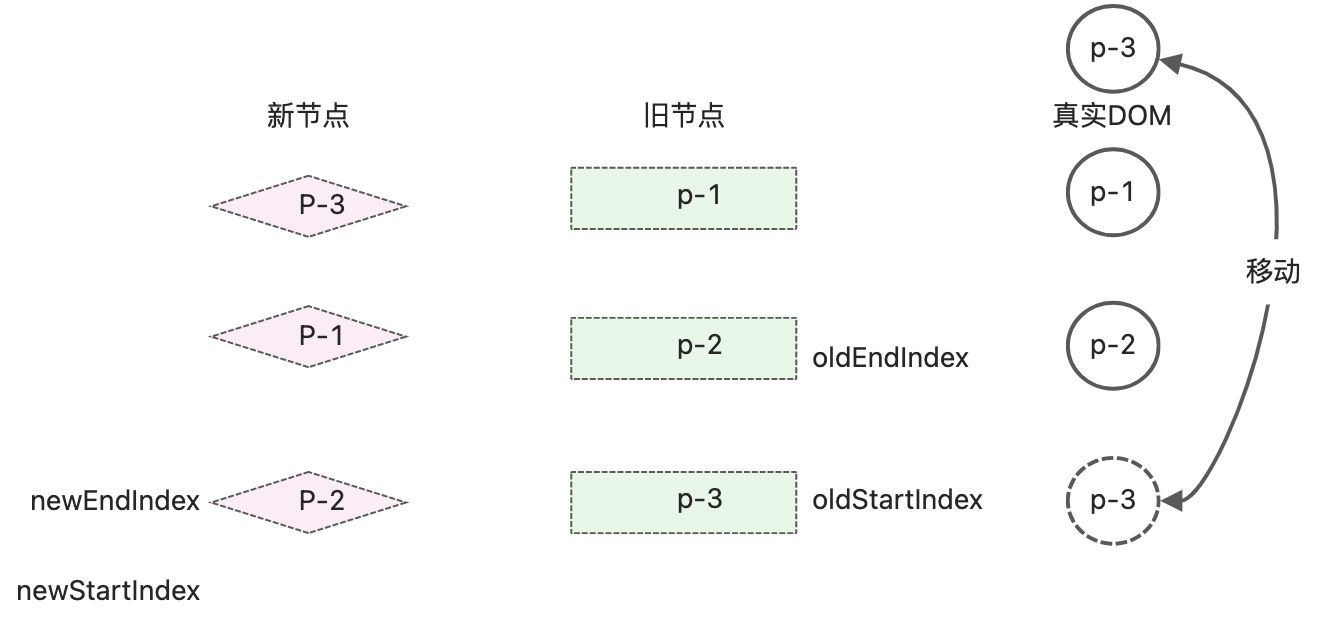
完成了所有的diff算法，进行了3次vnode对比，1次DOM移动。

10.3处理非理想状态

上面的示例节点处理，正好可以命中while循环的四个if判断，在非理想情况下，如果四个判断都无法命中，接下来该怎么操作？如下图的节点移动

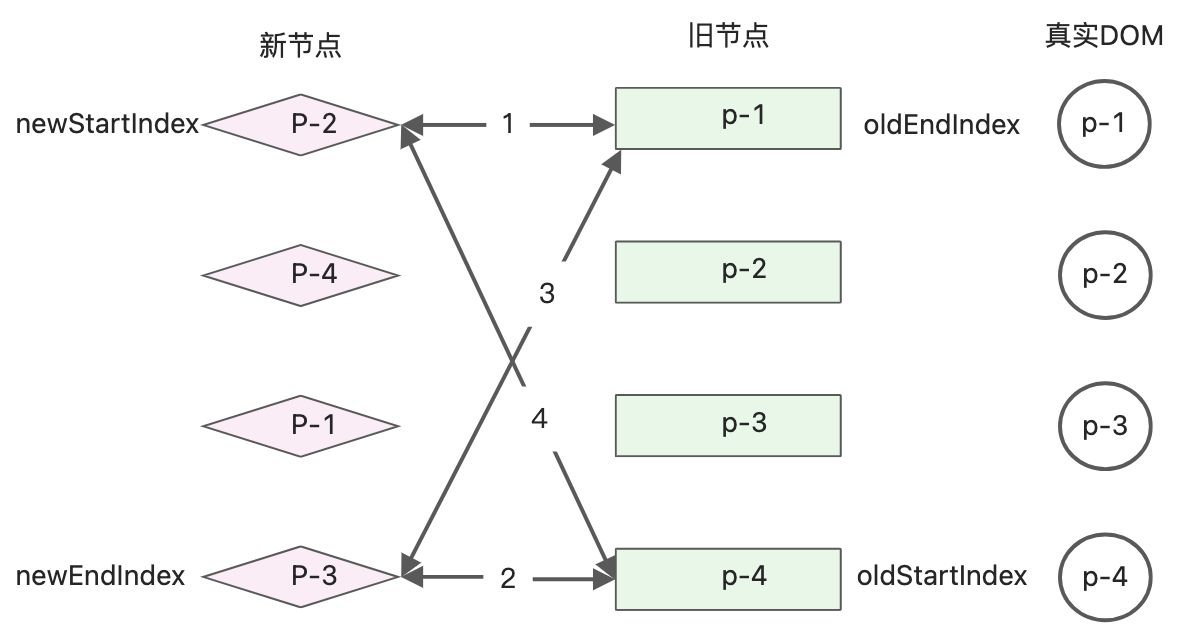
新旧两组节点的顺序

• 旧子节点：p-1、p-2、p-3、p-4
• 新子节点：p-2、p-4、p-1、p-3

进行while循环的diff更新，发现现在的4个if分支都无法满足条件。因此增加额外的处理逻辑

while(oldStartIndex <= oldEndIndex && newStartIndex <= newEndIndex){
  if(oldStartVnode.key === newStartVnode.key){
    // oldStartIndex 和 newStartIndex对比
    // 进入判断条件 p-2节点的对比，调用patch函数，对oldStartVnode和newStartVnode打补丁
    patch(oldStartVnode, newStartVnode, container);
    // 更新相关索引，指向下一个位置
    oldStartVnode  = oldChildren[++oldStartIndex];
    newStartVnode = newChildren[++newStartIndex];
  }else if(oldEndVnode.key === newEndVnode.key){
    // oldEndIndex 和 newEndIndex对比
  }else if(oldStartVnode.key === newEndVnode.key){
    // oldStartIndex 和 newEndIndex 对比
    // 旧的头部p-1 和 新的尾部p-1相同，进入这个判断条件
    // oldStartVnode newEndVnode节点进行打补丁操作
    patch(oldStartVnode, newEndVnode, container);
    // 将旧头部节点对于的dom oldStartVnode.el 移动到旧尾部节点对应的DOM节点后边
    insert(oldStartVnode.el, container, oldEndVnode.el.nextSibling);
    // 更新索引值
    oldStartVnode = oldChildren[++oldEndIndex];
    newEndVnode = newChildren[--newEndIndex];
  }else if(oldEndVnode.key === newStartVnode.key){
    // oldEndIndex 和 newStartIndex 对比
  }else{ // 这里是新增的逻辑判断
   // 遍历旧的子节点，寻找与newStartVnode节点有相同key的节点
    // idxInOld找出新的节点在旧的一组节点中的索引
    const idxInOld = oldChildren.findIndex(
      node => node.key === newStartVnode.key;
    )
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

用新的子节点的头部节点p-2，去旧的一组子节点中查找，找到了可复用的节点，索引位置为1。这意味着节点p-2原本不是头部节点，更新后变成了头部节点，需要移动p-2对应的真实DOM到当前旧的节点的头部p-1所对应的真实DOM之前。代码实现如下：

while(oldStartIndex <= oldEndIndex && newStartIndex <= newEndIndex){
  if(oldStartVnode.key === newStartVnode.key){
    // oldStartIndex 和 newStartIndex对比
    // 进入判断条件 p-2节点的对比，调用patch函数，对oldStartVnode和newStartVnode打补丁
    patch(oldStartVnode, newStartVnode, container);
    // 更新相关索引，指向下一个位置
    oldStartVnode  = oldChildren[++oldStartIndex];
    newStartVnode = newChildren[++newStartIndex];
  }else if(oldEndVnode.key === newEndVnode.key){
    // oldEndIndex 和 newEndIndex对比
  }else if(oldStartVnode.key === newEndVnode.key){
    // oldStartIndex 和 newEndIndex 对比
    // 旧的头部p-1 和 新的尾部p-1相同，进入这个判断条件
    // oldStartVnode newEndVnode节点进行打补丁操作
    patch(oldStartVnode, newEndVnode, container);
    // 将旧头部节点对于的dom oldStartVnode.el 移动到旧尾部节点对应的DOM节点后边
    insert(oldStartVnode.el, container, oldEndVnode.el.nextSibling);
    // 更新索引值
    oldStartVnode = oldChildren[++oldEndIndex];
    newEndVnode = newChildren[--newEndIndex];
  }else if(oldEndVnode.key === newStartVnode.key){
    // oldEndIndex 和 newStartIndex 对比
  }else{ // 这里是新增的逻辑判断
   // 遍历旧的子节点，寻找与newStartVnode节点有相同key的节点
    // idxInOld找出新的节点在旧的一组节点中的索引
    const idxInOld = oldChildren.findIndex(
      node => node.key === newStartVnode.key;
    )
    //如果idxInOld大于0，说明有可复用的节点，需要移动真实DOM节点
    if(idxInOld > 0){
      // idxInOld位置对应的vnode就是需要移动的节点
      const vnodeToMove = oldChildren[idxInOld];
      // 对移动的节点进行patch 打补丁
      patch(vnodeToMove, newStartVnode, container);
      // 将移动的节点对应的DOM【vnodeToMove.el】移动到旧头部节点对应的DOM【oldStartVnode.el】之前
      insert(vnodeToMove.el, container, oldStartVnode.el);
      // 由于idxInOld位置的节点的真实DOM发生了移动，因此该位置设置为undefined
      oldChildren[idxInOld] = undefined;
      //最后更新 newStartIdx的值
      newStartVnode = newChildren[++newStartIdx];
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

代码中先判断idxInOld是否大于0，如果大于0说明找到了可以复用的节点，然后将该节点对应的DOM进行移动。

• patch节点
• 移动节点对应的真实DOM
• 调整idxInOld处节点的值，oldChildren[idxInOld] = undefined
• 更新newStartIdx的索引值

操作之后，新旧节点及真实DOM节点的状态：

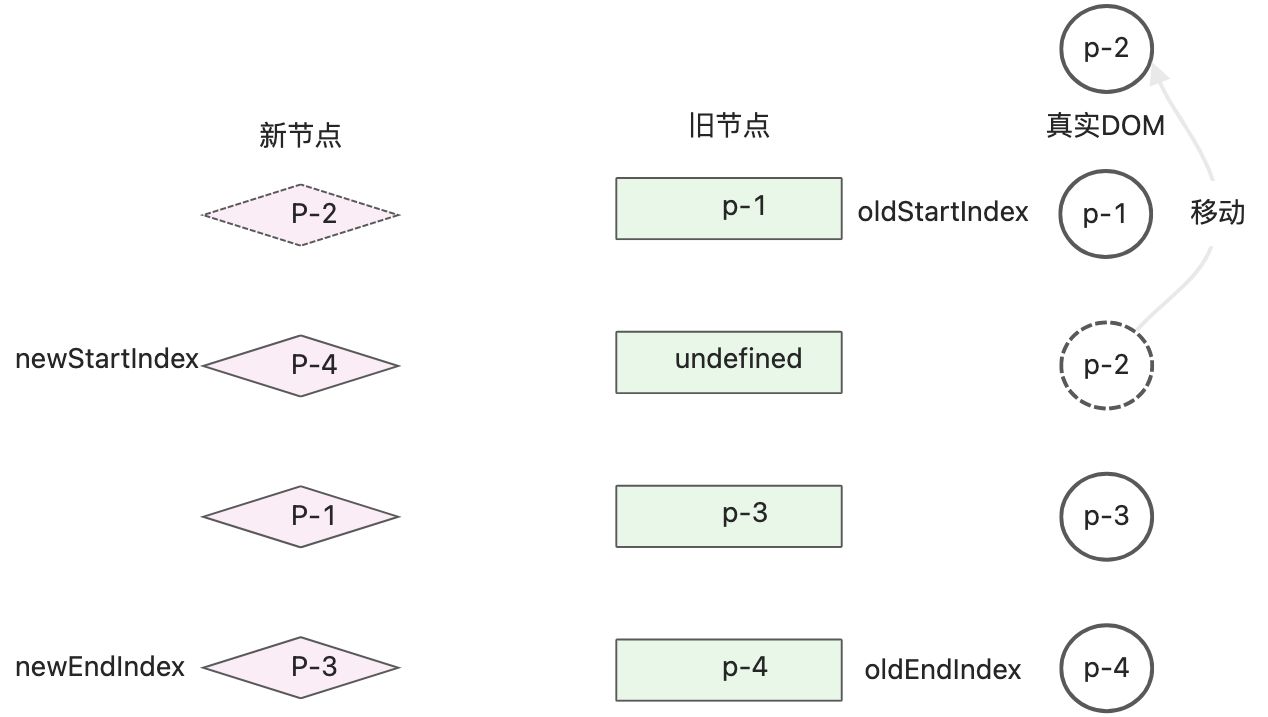
真实DOM的顺序为： p-2、p-1、p-3、p-4
继续进行双端Diff算法

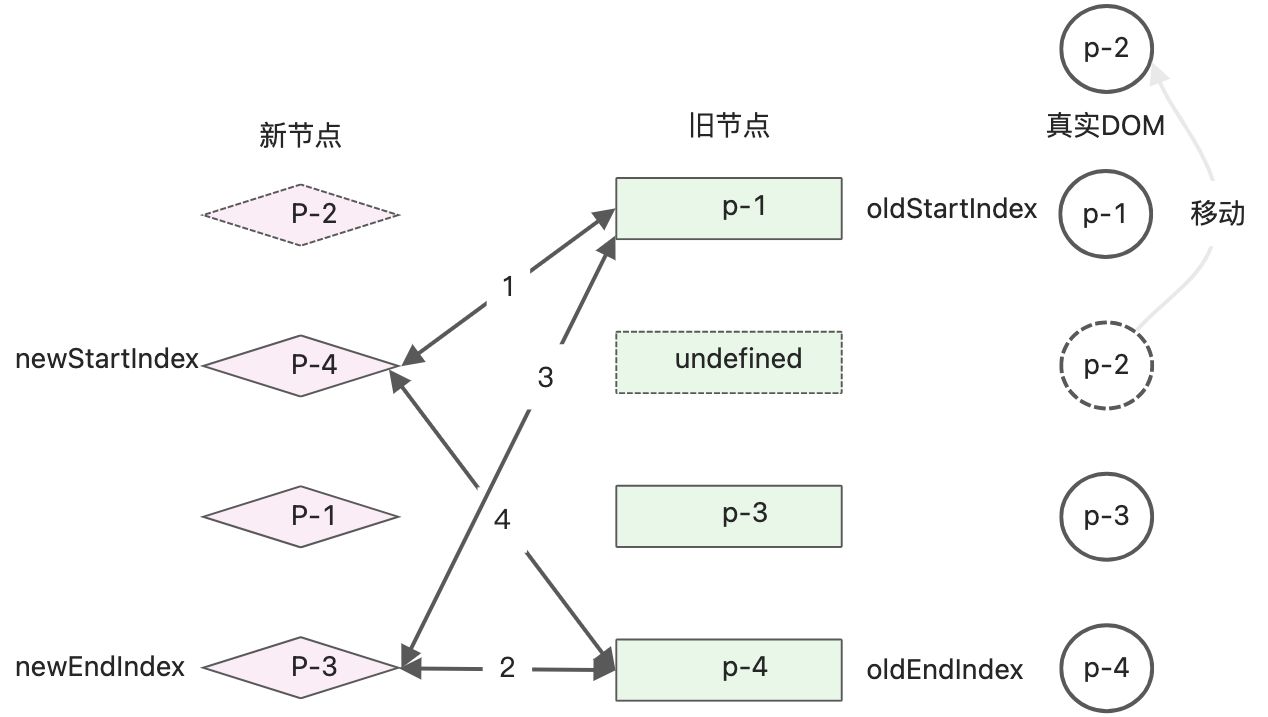
继续进行while的判断，可以命中尾头判断，就是oldEndVnode和newStartVnode的key相同。

else if(oldEndVnode.key === newStartVnode.key){ // 尾头
  // 第四步：oldEndVnode 和 newStartVnode
  //使用patch函数进行打补丁
  patch(oldEndVnode, newStartVnode, container);
  // 移动DOM操作
  // oldEndVnode.el 移动到 oldStartVnode.el前面
  insert(oldEndVnode.el, container, oldStartVnode.el)

  // 移动DOM完成后，更新索引值，并指向下一个位置
  oldEndVnode = oldChildren[--oldEndIndex];
  newStartVnode = newChildren[++newStartIndex];
}
1
2
3
4
5
6
7
8
9
10
11
12

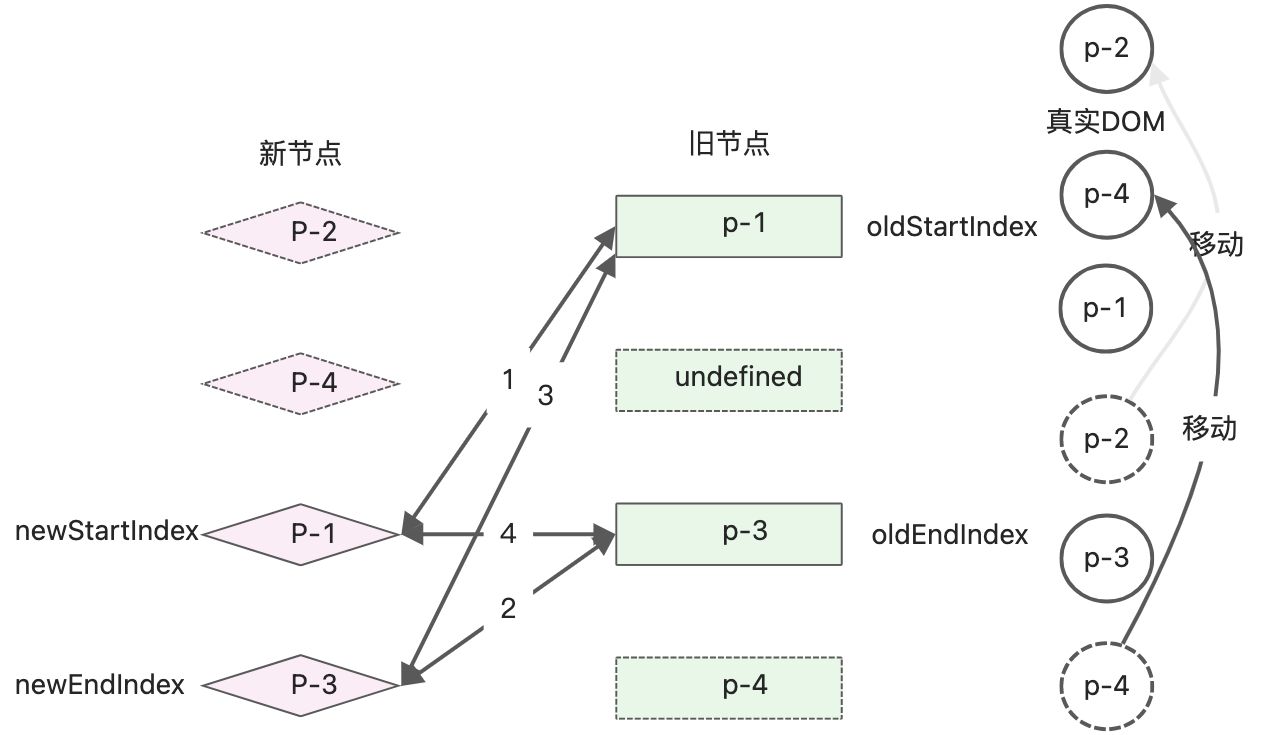
操作对比之后，真实DOM节点的顺序：p-2、p-4、p-1、p-3。
然后进行下一轮的Diff对比。对比新旧节点，发现头头节点的key相同，可以复用，不需要移动真实DOM，只用patch对节点进行打补丁。
经过对比p-1节点后，新旧子节点与真实DOM的状态如下图

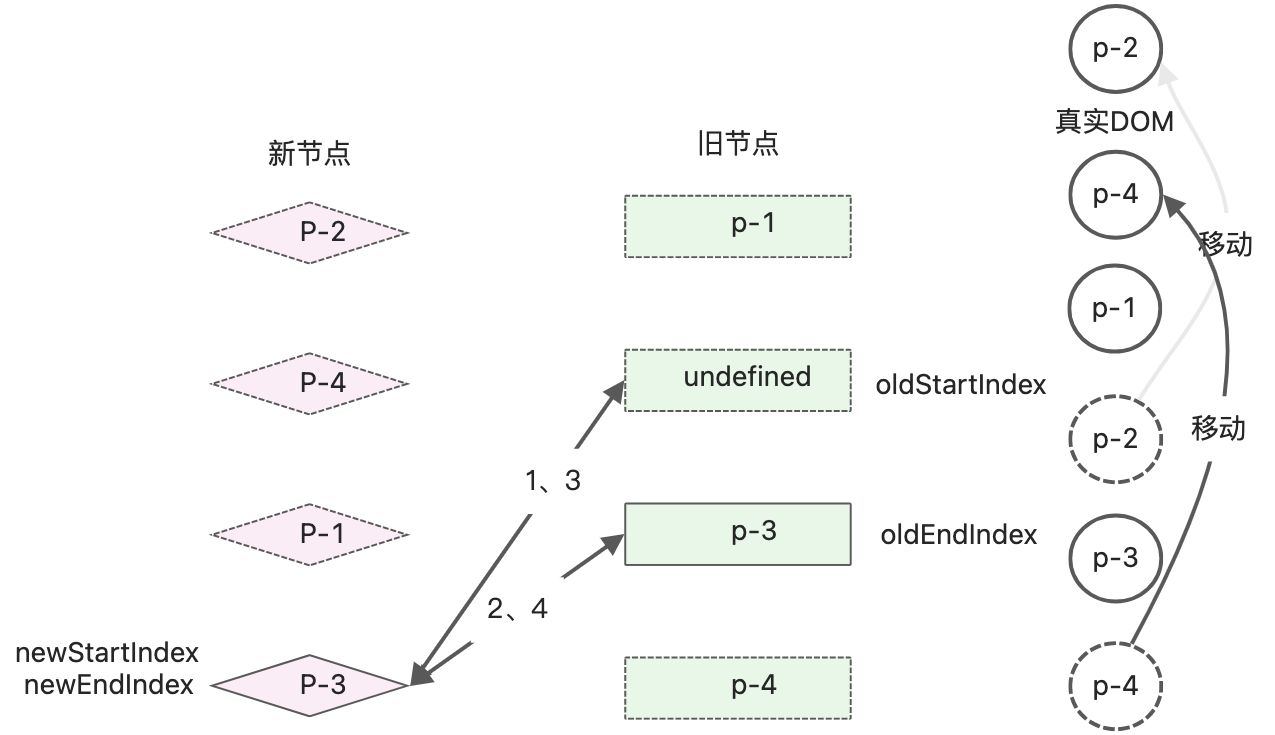
真实DOM节点的顺序：p-2、p-4、p-1、p-3。接着继续进行下一轮的diff计算。此时旧的头节点值为undefined，说明该节点已经被处理过，直接跳过即可。修改while的逻辑

while(oldStartIndex <= oldEndIndex && newStartIndex <= newEndIndex){
  if(!oldStartVnode){ //处理旧节点开头为undefined
    oldStartVnode = oldChildren[++oldStartIndex];
  }eles if(!oldEndVnode){ //处理旧节点结尾为undefined
    oldEndVnode = oldChildren[--oldEndIndex];
  }else if(oldStartVnode.key === newStartVnode.key){
    // oldStartIndex 和 newStartIndex对比
    // 进入判断条件 p-2节点的对比，调用patch函数，对oldStartVnode和newStartVnode打补丁
    patch(oldStartVnode, newStartVnode, container);
    // 更新相关索引，指向下一个位置
    oldStartVnode  = oldChildren[++oldStartIndex];
    newStartVnode = newChildren[++newStartIndex];
  }else if(oldEndVnode.key === newEndVnode.key){
    // oldEndIndex 和 newEndIndex对比
  }else if(oldStartVnode.key === newEndVnode.key){
    // oldStartIndex 和 newEndIndex 对比
    // 旧的头部p-1 和 新的尾部p-1相同，进入这个判断条件
    // oldStartVnode newEndVnode节点进行打补丁操作
    patch(oldStartVnode, newEndVnode, container);
    // 将旧头部节点对于的dom oldStartVnode.el 移动到旧尾部节点对应的DOM节点后边
    insert(oldStartVnode.el, container, oldEndVnode.el.nextSibling);
    // 更新索引值
    oldStartVnode = oldChildren[++oldEndIndex];
    newEndVnode = newChildren[--newEndIndex];
  }else if(oldEndVnode.key === newStartVnode.key){
    // oldEndIndex 和 newStartIndex 对比
  }else{ // 这里是新增的逻辑判断
   // 遍历旧的子节点，寻找与newStartVnode节点有相同key的节点
    // idxInOld找出新的节点在旧的一组节点中的索引
    const idxInOld = oldChildren.findIndex(
      node => node.key === newStartVnode.key;
    )
    //如果idxInOld大于0，说明有可复用的节点，需要移动真实DOM节点
    if(idxInOld > 0){
      // idxInOld位置对应的vnode就是需要移动的节点
      const vnodeToMove = oldChildren[idxInOld];
      // 对移动的节点进行patch 打补丁
      patch(vnodeToMove, newStartVnode, container);
      // 将移动的节点对应的DOM【vnodeToMove.el】移动到旧头部节点对应的DOM【oldStartVnode.el】之前
      insert(vnodeToMove.el, container, oldStartVnode.el);
      // 由于idxInOld位置的节点的真实DOM发生了移动，因此该位置设置为undefined
      oldChildren[idxInOld] = undefined;
      //最后更新 newStartIdx的值
      newStartVnode = newChildren[++newStartIdx];
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

直接跳过进入下个节点，此时新旧节点和真实DOM节点的状态

现在4个步骤发生重合，接着进行while循环，发现头头节点的key相同，节点可以复用，进行patch打补丁操作。
因为此时新旧节点都属于头部节点，并不需要移动DOM。然后更新指针索引。
新旧节点和真实DOM节点的状态如下

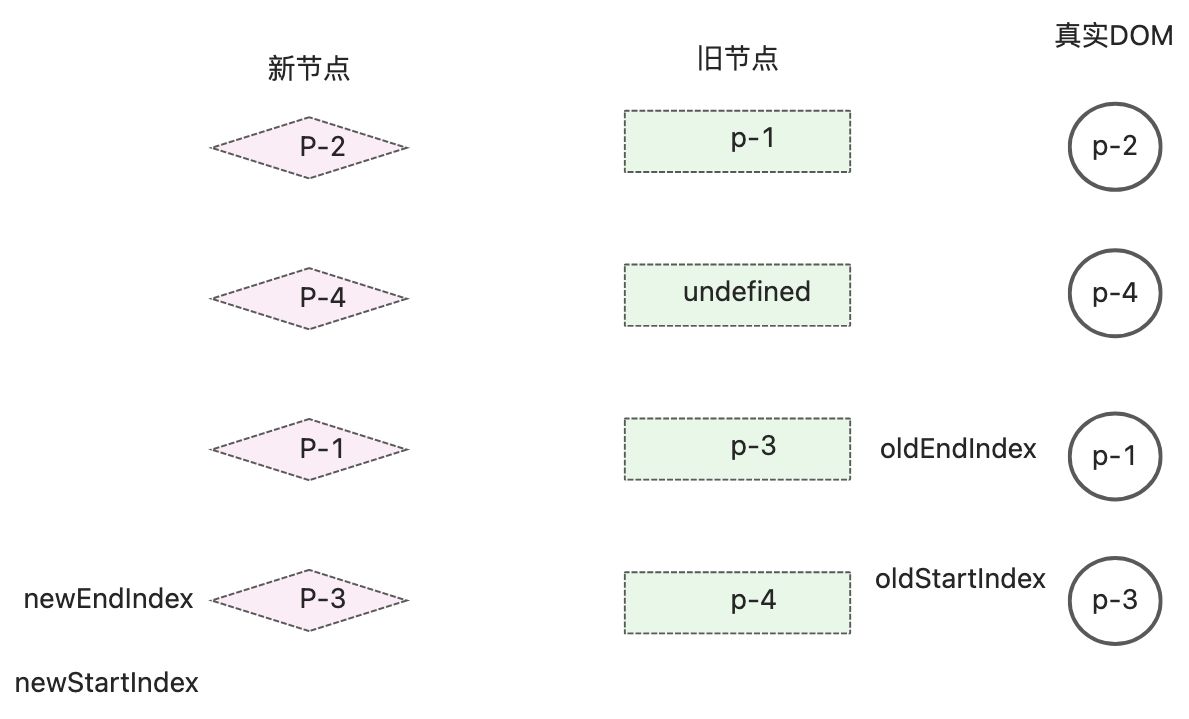
满足了while循环的终止条件，更新完成，最终真实DOM的顺序和新的子节点的顺序一致。
代码示例

10.4添加新元素

接下来处理另外一个特殊情况：

• 旧子节点：p-1、p-2、p-3
• 新子节点：p-4、p-1、p-3、p-2

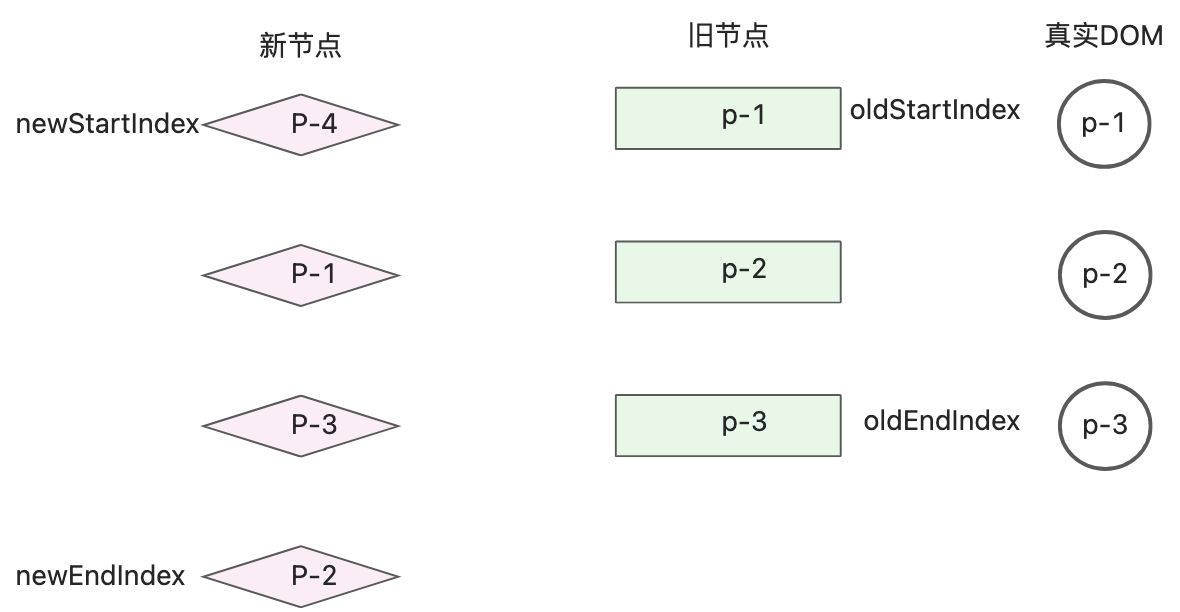
用新的子节点头部p-4，在旧的子节点中查找，无法找到可复用的节点，说明p-4是新增的节点。
因为p-4是新子节点的头部节点，所以只需将它挂载到当前头部节点之前，当前头部指的是旧的子节点头部所对应的DOM节点p-1。用代码完成操作

while(oldStartIndex <= oldEndIndex && newStartIndex <= newEndIndex){
  if(!oldStartVnode){ //处理旧节点开头为undefined
    oldStartVnode = oldChildren[++oldStartIndex];
  }eles if(!oldEndVnode){ //处理旧节点结尾为undefined
    oldEndVnode = oldChildren[--oldEndIndex];
  }else if(oldStartVnode.key === newStartVnode.key){
    // oldStartIndex 和 newStartIndex对比
    // 进入判断条件 p-2节点的对比，调用patch函数，对oldStartVnode和newStartVnode打补丁
    patch(oldStartVnode, newStartVnode, container);
    // 更新相关索引，指向下一个位置
    oldStartVnode  = oldChildren[++oldStartIndex];
    newStartVnode = newChildren[++newStartIndex];
  }else if(oldEndVnode.key === newEndVnode.key){
    // oldEndIndex 和 newEndIndex对比
  }else if(oldStartVnode.key === newEndVnode.key){
    // oldStartIndex 和 newEndIndex 对比
    // 旧的头部p-1 和 新的尾部p-1相同，进入这个判断条件
    // oldStartVnode newEndVnode节点进行打补丁操作
    patch(oldStartVnode, newEndVnode, container);
    // 将旧头部节点对于的dom oldStartVnode.el 移动到旧尾部节点对应的DOM节点后边
    insert(oldStartVnode.el, container, oldEndVnode.el.nextSibling);
    // 更新索引值
    oldStartVnode = oldChildren[++oldEndIndex];
    newEndVnode = newChildren[--newEndIndex];
  }else if(oldEndVnode.key === newStartVnode.key){
    // oldEndIndex 和 newStartIndex 对比
  }else{ // 这里是新增的逻辑判断
   // 遍历旧的子节点，寻找与newStartVnode节点有相同key的节点
    // idxInOld找出新的节点在旧的一组节点中的索引
    const idxInOld = oldChildren.findIndex(
      node => node.key === newStartVnode.key;
    )
    //如果idxInOld大于0，说明有可复用的节点，需要移动真实DOM节点
    if(idxInOld > 0){
      // idxInOld位置对应的vnode就是需要移动的节点
      const vnodeToMove = oldChildren[idxInOld];
      // 对移动的节点进行patch 打补丁
      patch(vnodeToMove, newStartVnode, container);
      // 将移动的节点对应的DOM【vnodeToMove.el】移动到旧头部节点对应的DOM【oldStartVnode.el】之前
      insert(vnodeToMove.el, container, oldStartVnode.el);
      // 由于idxInOld位置的节点的真实DOM发生了移动，因此该位置设置为undefined
      oldChildren[idxInOld] = undefined;
      //最后更新 newStartIdx的值
      newStartVnode = newChildren[++newStartIdx];
    }
    // ++++++++++新增内容+++++++++++++
    else{ //无法在旧节点找到对应的值
      // 将newStartVnode作为新节点挂载到头部，使用当前头部节点 oldStartVnode.el作为锚点
      patch(null, newStartVnode, container, oldStartVnode.el);
    }
    newStartVnode = newChildren[++newStartIdx]
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

如上代码，当idxInOld>0不成立，说明newStartVnode节点是全新的节点，newStartVnode又是头部节点，应该将其作为新的头部节点进行挂载。
新节点p-4挂载完成后，新旧节点和真实DOM节点的状态

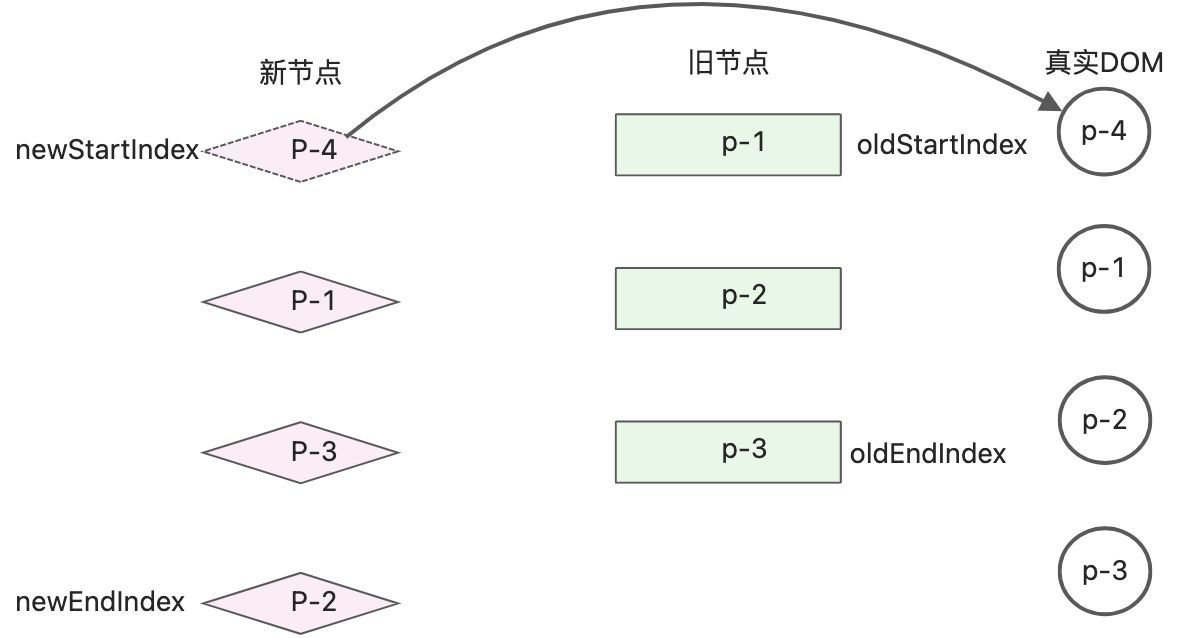
上面的这个例子比较特殊，由于无法命中while中的头头、尾尾、头尾、尾头判断，而进入到了最后的else判断分支，可以将新的开始节点从旧节点中进行查找操作。
如果调整下顺序’：

• 旧子节点：p-1、p-2、p-3
• 新子节点：p-4、p-1、p-2、p-3

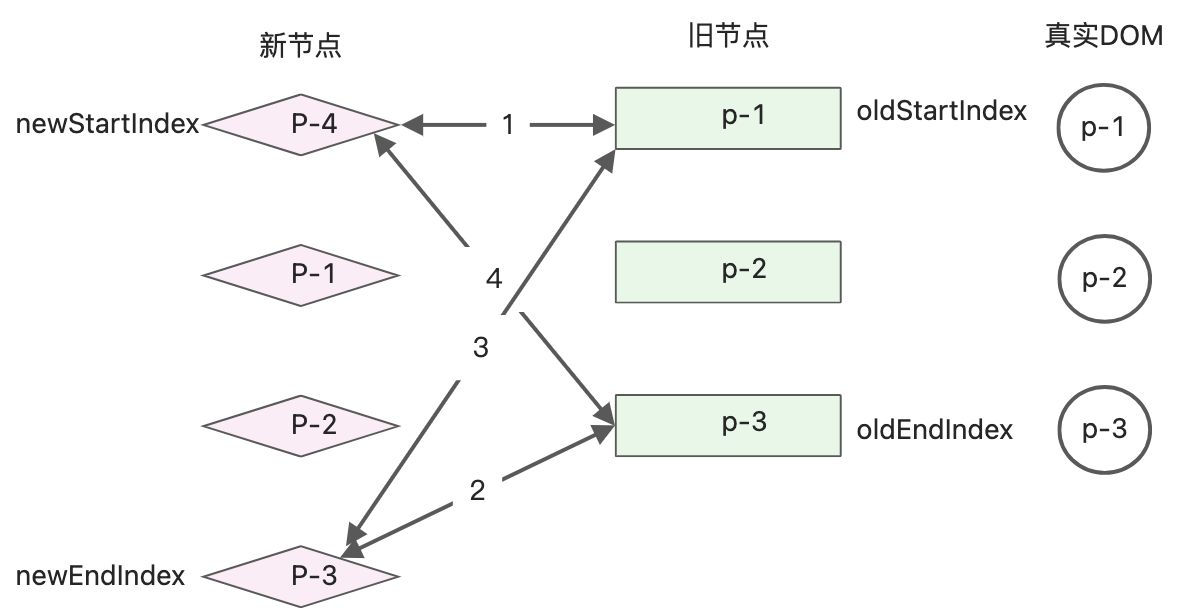
按照双端Diff进行更新，进入到尾尾相同的判断分支

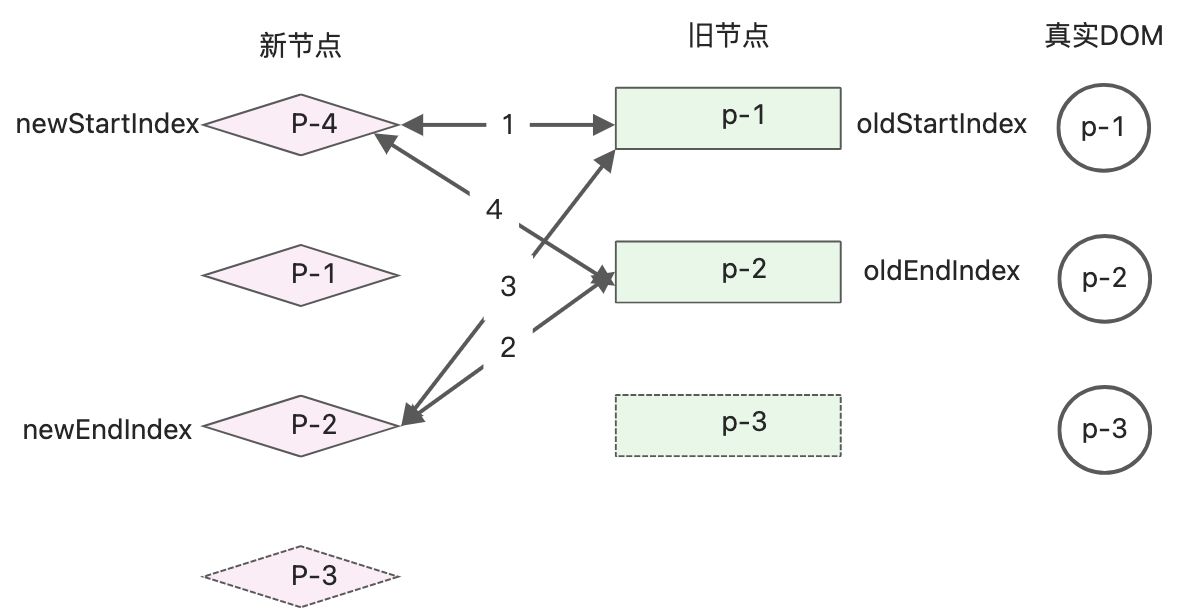
继续进行下一轮diff判断，仍然进入尾尾相同的判断分支

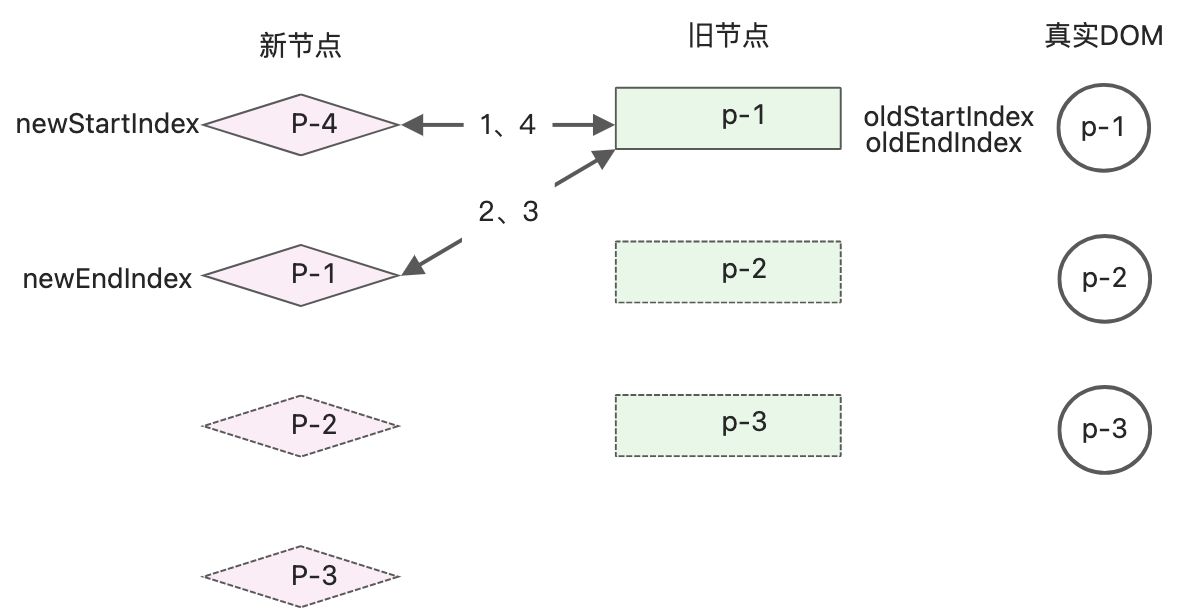
继续进行下一轮diff判断，仍然进入尾尾相同的判断分支

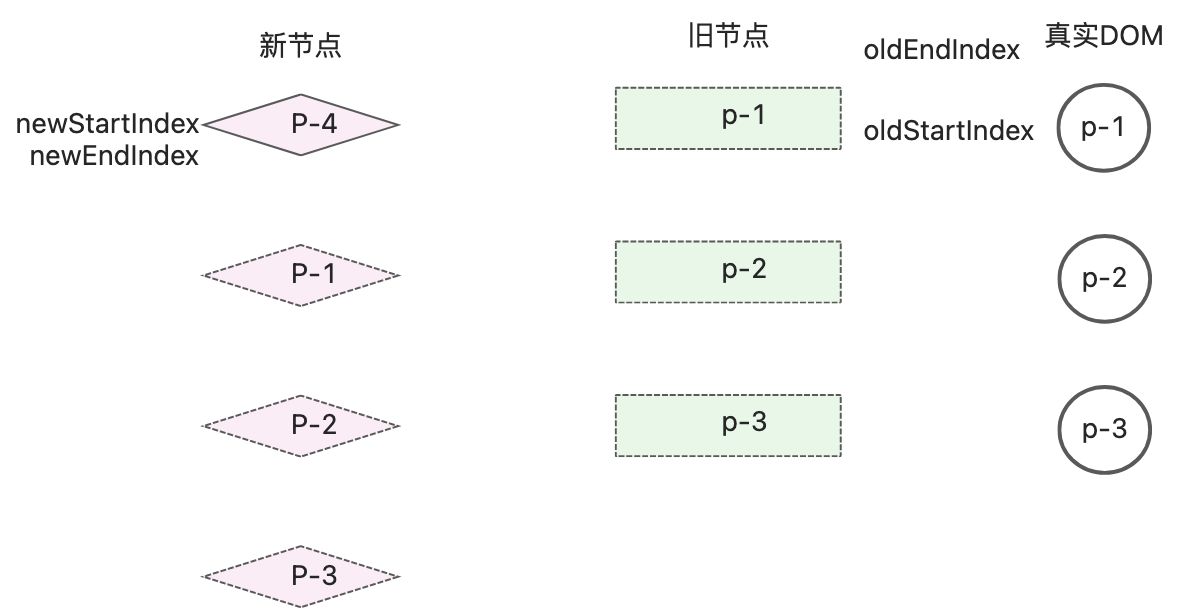
此时更新完成后，由于oldEndIndx值小于oldStartIndex的值，无法进行while循环判断。diff停止更新，但是通过观察可以发现节点p-4在整个更新过程中被遗漏，为了修复这个bug，需要在while循环结束后增加if条件语句。
如果oldEndIdx < oldStartIdx && newStartIdx <= newEndIdx成立，说明新的子节点中有遗留的新增节点。

• 索引值位于newStartIdx 和newEndIdx区间的节点都是新增节点。
• 挂载时的锚点仍然使用当前的头部节点oldStartVnode.el

while(oldStartIndex <= oldEndIndex && newStartIndex <= newEndIndex){
 //...
}
if(oldEndIndex< oldStartIndex && newStartIndex <= newEndIndex){
  //如果满足条件，说明新节点有遗留，需要挂载他们
  for(let i=newStartIndex; i<=newEndIndex; i++){
    patch(null, newChildren[i], container, oldStartVnode.el)
  }
}
1
2
3
4
5
6
7
8
9

这样就完成了对新增元素的处理。
代码示例

10.5移动不存在的元素

处理过了新增元素，另外还要处理新节点的删除元素。

• 旧子节点：p-1、p-2、p-3
• 新子节点：p-1、p-3

新节点中删除了p-2节点。
执行双端diff更新，进入头头节点相同的分支，

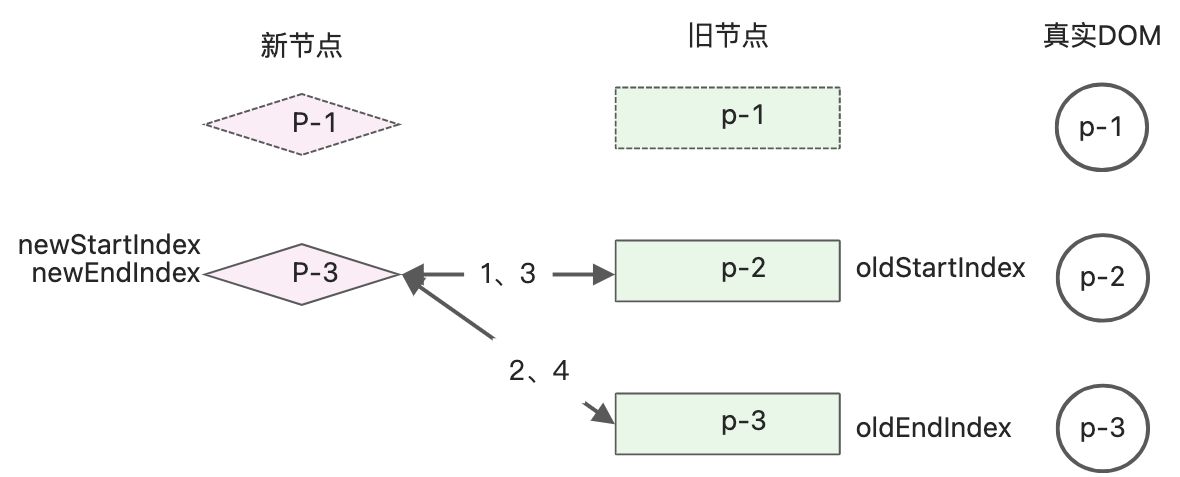
再次执行双端diff更新，进入尾头节点相同的分支

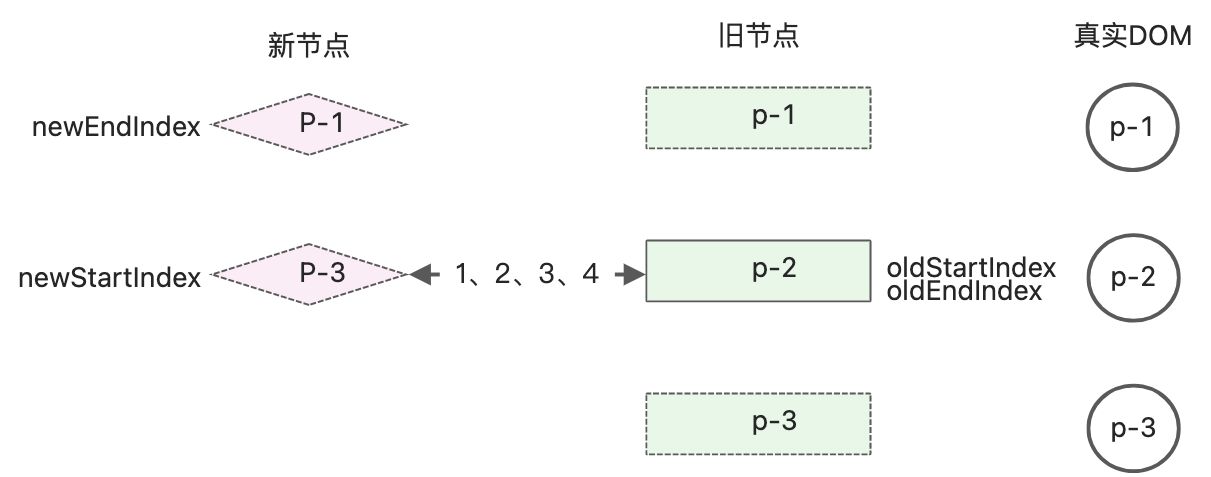
到这里发现变量newStartIndex不小于等于newEndIndex的值，跳出while循环，但是旧的子节点中仍然存在未被处理的节点，应该将其移除。在while循环外，添加if判断分支

while(oldStartIndex <= oldEndIndex && newStartIndex <= newEndIndex){
 //...
}
if(oldEndIndex< oldStartIndex && newStartIndex <= newEndIndex){
  //如果满足条件，说明新节点有遗留，需要挂载他们
  for(let i=newStartIndex; i<=newEndIndex; i++){
    patch(null, newChildren[i], container, oldStartVnode.el)
  }
}else if(newEndIndex < newStartIndex&& oldStartIndex <= oldEndIndex){
 // 移除节点操作
  for(let i=oldStartIndex;i<= oldEndIndex; i++){
    unmount(oldChildren[i])
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

和处理新增节点类似，在while循环外新增if判断分支，使用for循环卸载[oldStartIndex, oldEndIndex]区间不存在的节点。
代码示例

11.快速diff算法-ivi和inferno【vue3中的diff算法】

快速diff算法相对双端diff算法更进一步优化。可在节点diff的过程中找出最长递增子序列，这个序列中的节点顺序是相对不发生变化的，所以可以更进一步的减少DOM移动操作。快速diff算法还包含预处理步骤，预处理会处理相同的前缀和后缀部分。

11.1处理前置和后置元素

快速diff算法借鉴纯文本diff算法中预处理的步骤。

新增节点

一组新旧子节点如下：

• p-1、p-2、p-3
• p-1、p-4、p-2、p-3

通过观察可以发现，新旧节点具有相同的前置节点p-1和相同的后置节点p-3、p-4。对于相同的前置和后置节点，他们在新旧两组节点中的相当位置不变，无需移动他们。

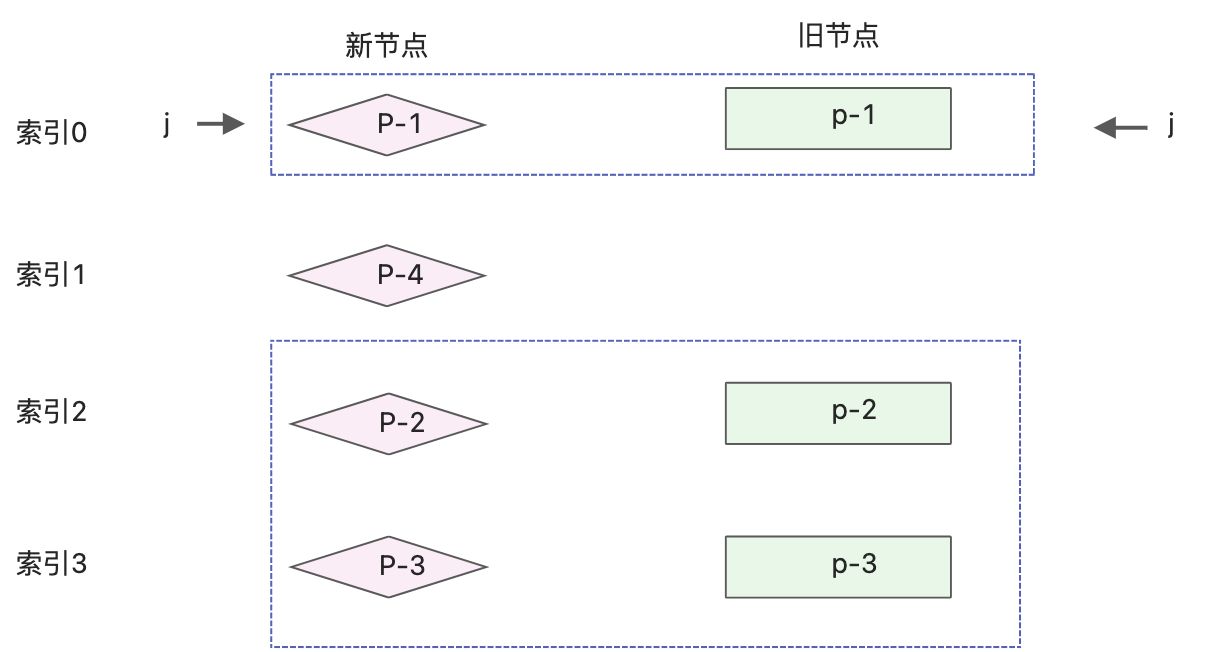
对于前置节点，可以建立索引J，初始值为0，用来指向两组子节点的开头。
开启while循环，让索引J递增，直到遇到不同的节点位置。调整patchKeyedChildren函数代码

function patchKeyedChildren(n1,n2, container){
  const newChildren = n2.children;
  const oldChildren = n1.children;
  // 处理相同的前置节点 ，索引J指向新旧两组子节点的开头
  let j =0;
  let oldVnode = oldChildren[j];
  let newVnode = newChildren[j];
  // while循环向后变量，直到遇到不同key 停止
  while(oldVnode.key === newVnode.key){
    //调用patch函数
    patch(oldVnode, newVnode, container);
    //更新索引J的值
    j++;
    oldVnode = oldChildren[j];
    newVnode = newChildren[j];
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

通过while循环查找出所有的相同的前置节点，并调用patch函数进行打补丁。遇到不同的key，停止循环。经过操作之后，新旧两组子节点的状态如下图：

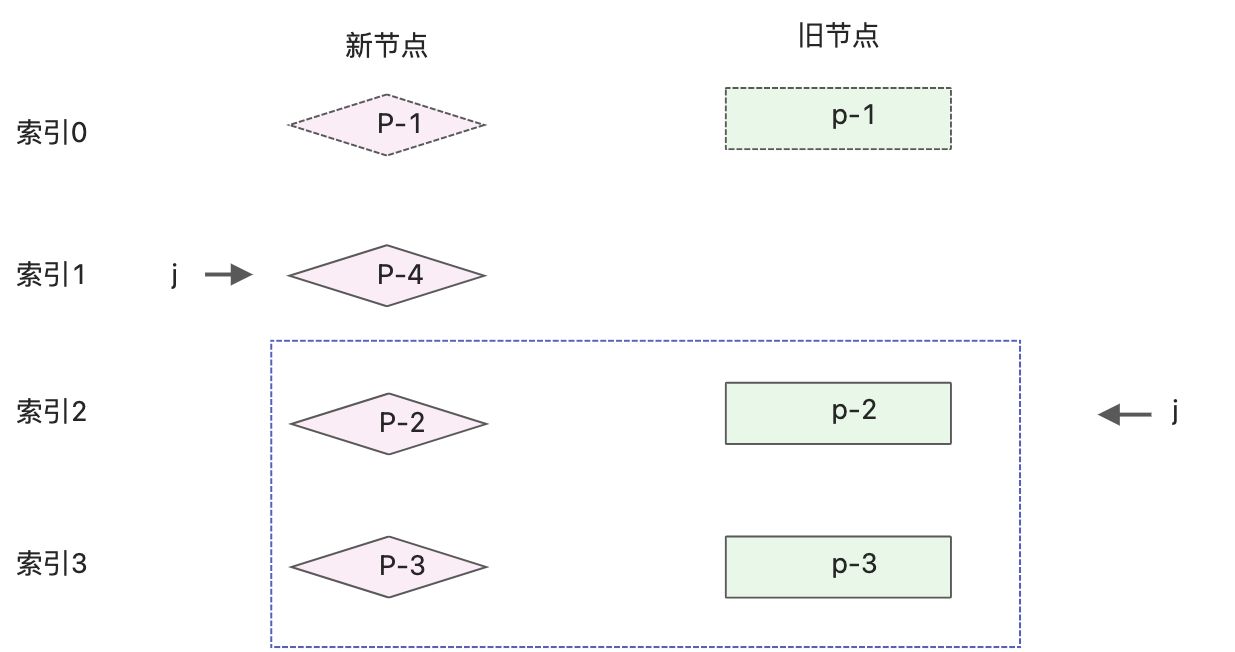
while停止循环，变量索引j的值为1。接下来处理相同的后置节点。
由于新旧两组子节点的数量可能不同，所以需要定义2个索引newEnd和oldEnd，分别指向新旧两组子节点中的最后一个节点。

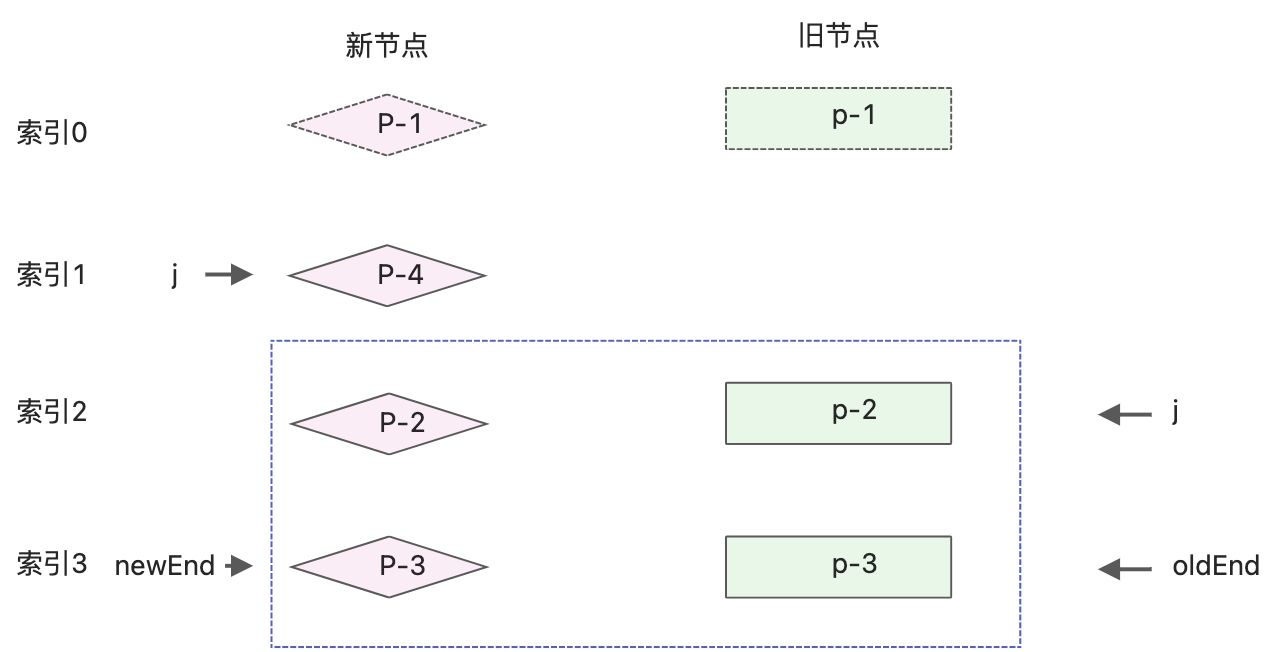
开启while循环，从尾向前开始变量，调整patchKeyedChildren函数

function patchKeyedChildren(n1,n2, container){
  const newChildren = n2.children;
  const oldChildren = n1.children;
  // 处理相同的前置节点 ，索引J指向新旧两组子节点的开头
  let j =0;
  let oldVnode = oldChildren[j];
  let newVnode = newChildren[j];
  // while循环向后变量，直到遇到不同key 停止
  while(oldVnode.key === newVnode.key){
    //调用patch函数
    patch(oldVnode, newVnode, container);
    //更新索引J的值
    j++;
    oldVnode = oldChildren[j];
    newVnode = newChildren[j];
  }
  
  // 更新相同的后置节点
  // 设置索引oldEnd，指向旧节点的最后一个
  let oldEnd = oldChildren.length -1;
  // 设置索引newEnd，指向新节点的最后一个
  let newEnd = newChildren.length - 1;
  oldVnode = oldChildren[oldEnd];
  newVnode = newChildren[newEnd];
  // 从后向前遍历，直到遇到不同的key停止
  while(oldVnode.key === newVnode.key){
    patch(oldVnode, newVnode, container);
    oldEnd--;
    newEnd--;
    oldVnode = oldChildren[oldEnd];
    newVnode = newChildren[newEnd];
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

后置节点处理完成后，更新oldEnd和newEnd的值，新旧两组子节点的状态如下：

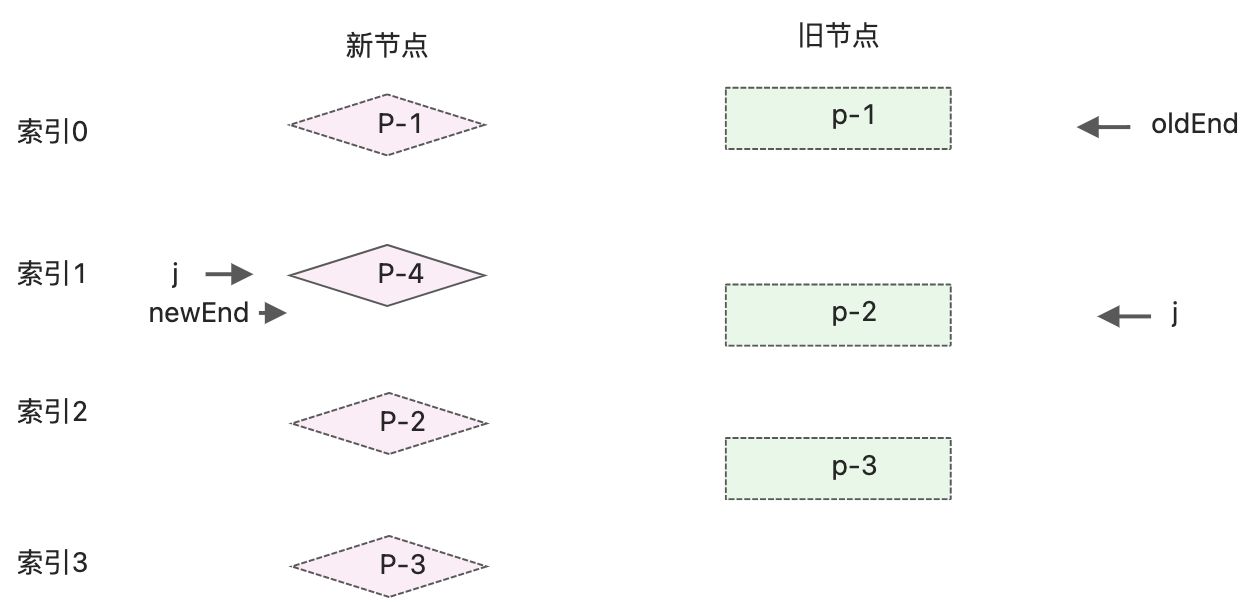
新旧子节点相同的前置和后置节点都被处理后，旧节点全部被处理，新节点遗留个节点p-4，说明该节点是新增节点。判断是新增节点的条件：

• oldEnd < j成立，说明旧节点全部被处理
• newEnd >= j成立，说明在预处理过后，在新的一组子节点中，仍然有未被处理的节点，这些节点就是新增节点。这个区间[j, newEnd]内的节点，都是新增节点。

function patchKeyedChildren(n1,n2, container){
  const newChildren = n2.children;
  const oldChildren = n1.children;
  
  // 处理相同的前置节点 ，索引J指向新旧两组子节点的开头
  let j =0;
  let oldVnode = oldChildren[j];
  let newVnode = newChildren[j];
  // while循环向后变量，直到遇到不同key 停止
  while(oldVnode.key === newVnode.key){
    //调用patch函数
    patch(oldVnode, newVnode, container);
    //更新索引J的值
    j++;
    oldVnode = oldChildren[j];
    newVnode = newChildren[j];
  }
  
  // 更新相同的后置节点
  // 设置索引oldEnd，指向旧节点的最后一个
  let oldEnd = oldChildren.length -1;
  // 设置索引newEnd，指向新节点的最后一个
  let newEnd = newChildren.length - 1;
  oldVnode = oldChildren[oldEnd];
  newVnode = newChildren[newEnd];
  // 从后向前遍历，直到遇到不同的key停止
  while(oldVnode.key === newVnode.key){
    patch(oldVnode, newVnode, container);
    oldEnd--;
    newEnd--;
    oldVnode = oldChildren[oldEnd];
    newVnode = newChildren[newEnd];
  }
  
  // 前置和后置预处理完毕后，还有剩余节点
  if(oldEnd < j && j <= newEnd){
    // 锚点索引
    const anchorIndex = newEnd + 1;
    const anchor = anchorIndex < newChildren.length ? newChildren[anchorIndex].el : null;
    // 采用while循环，调用patch函数，逐个挂载新增节点
    while(j <= newEnd){
     patch(null, newChildren[j++], container, anchor);
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

第39行判断锚点的取值。如果超过新节点的总长度，则为null，说明在最后追加元素。
第41行，开启while循环，遍历索引j和newEnd之间的节点，并调用patch函数挂载它们。

删除节点

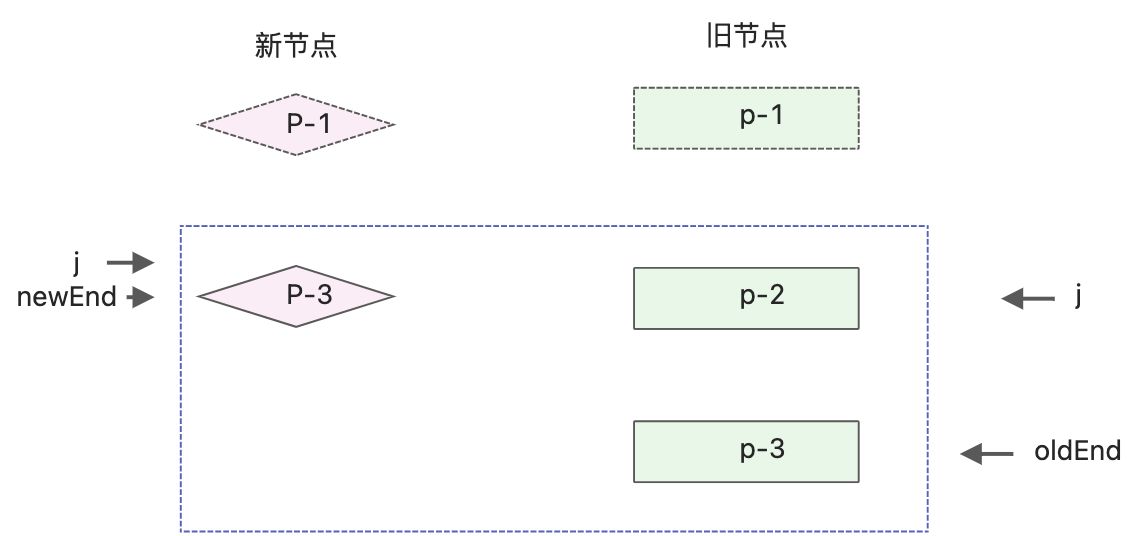
上面案例是新增节点，接下来处理删除节点。有两组子节点

• p-1、p-2、p-3
• p-1、p-3

同样使用 j、oldEnd、newEnd进行标记。

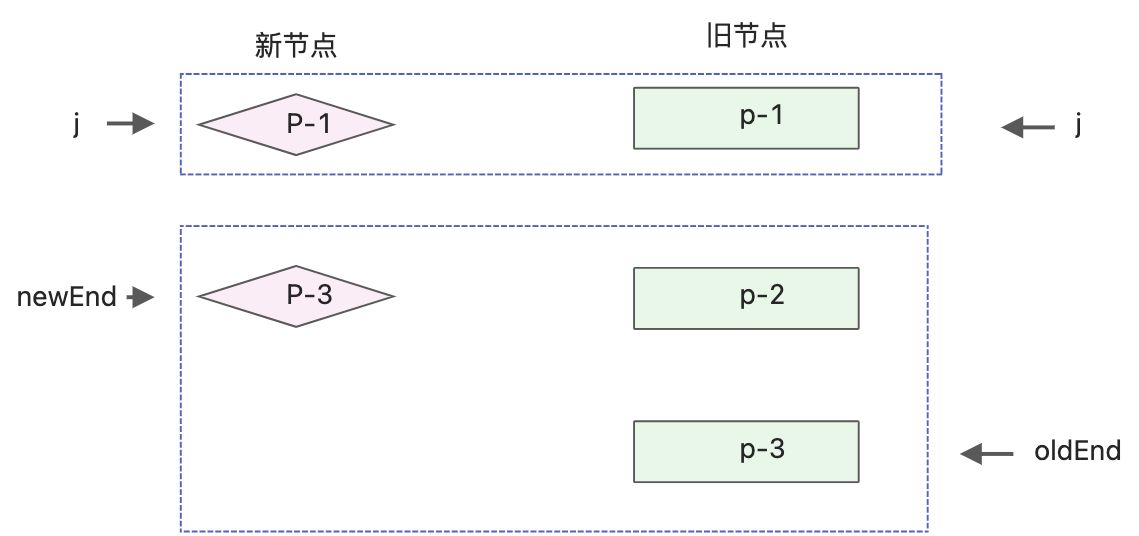
处理相同的前置节点，处理后的状态

处理相同的后置节点，处理后的状态

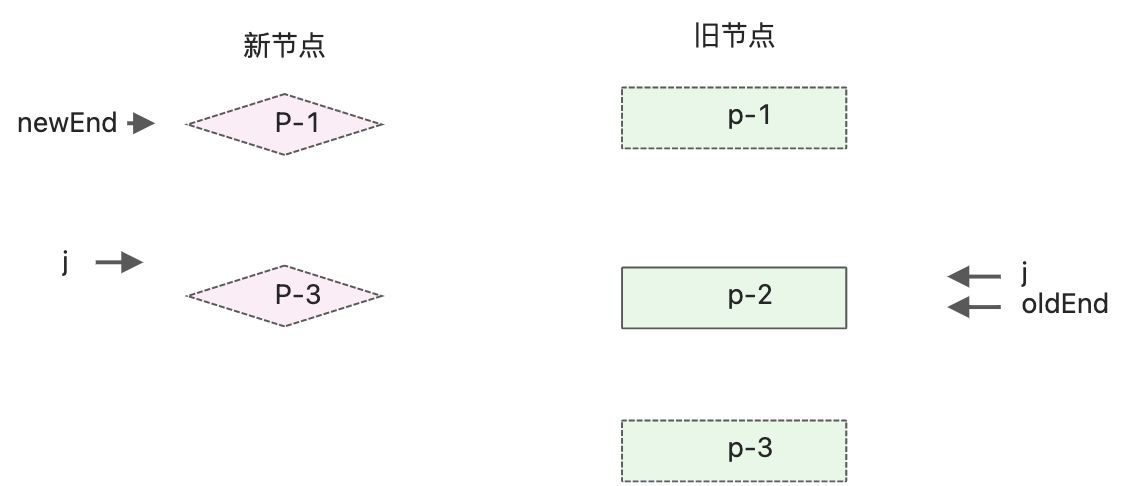
相同的前置和后置节点全部处理，此时新节点被全部处理，发现旧的一组子节点遗留了节点p-2。说明应该卸载区间[j, oldEnd]之间的元素。

function patchKeyedChildren(n1,n2, container){
  const newChildren = n2.children;
  const oldChildren = n1.children;
  
  // 处理相同的前置节点 ，索引J指向新旧两组子节点的开头
  // ...
  
  // 更新相同的后置节点
  // 设置索引oldEnd，指向旧节点的最后一个
  // ...
  
  // 前置和后置预处理完毕后，还有剩余节点
  if(oldEnd < j && j <= newEnd){
    // 锚点索引
    const anchorIndex = newEnd + 1;
    const anchor = anchorIndex < newChildren.length ? newChildren[anchorIndex].el : null;
    // 采用while循环，调用patch函数，逐个挂载新增节点
    while(j <= newEnd){
     patch(null, newChildren[j++], container, anchor);
    }
  }else if(newEnd < j && j <= oldEnd){
    while(j<=oldEnd){ //卸载j 和 oldEnd之前的元素。
      unmount(oldChildren[j++])
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

代码示例

⭐️11.2判断是否需要DOM移动

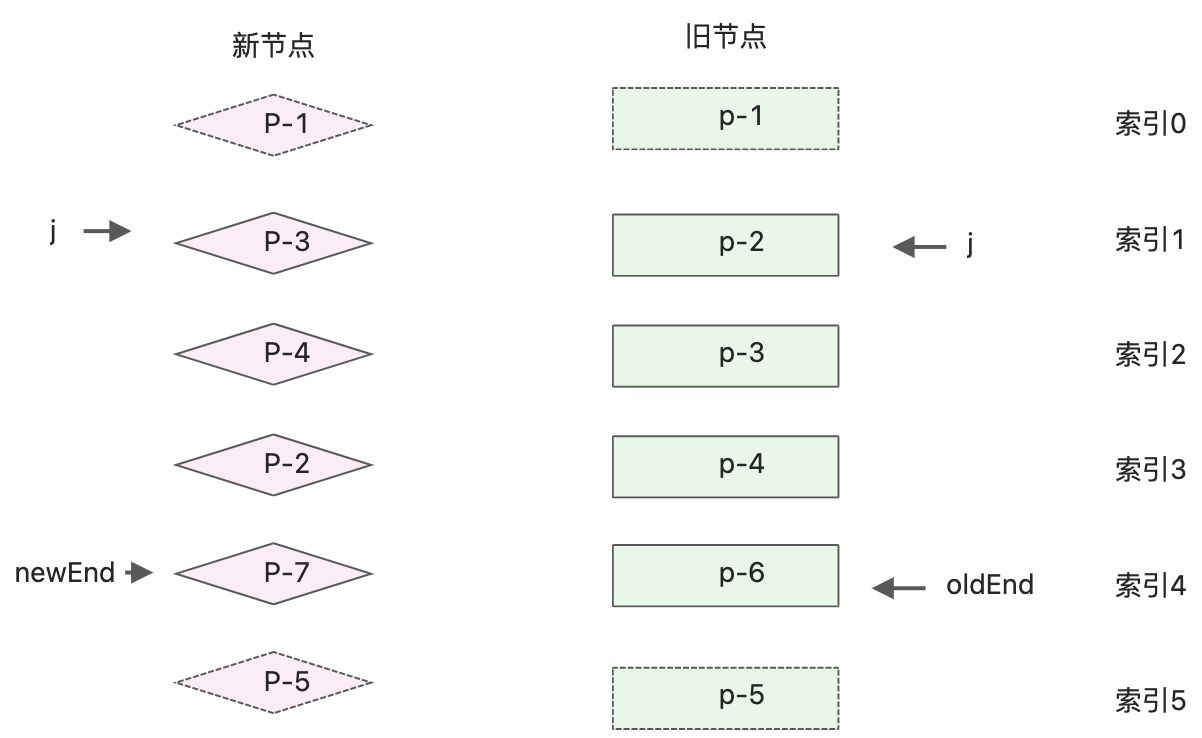
上节介绍了预处理前置节点和后置节点，并简单处理了新增节点和删除节点的逻辑，并没有处理复杂的移动元素操作。使用一个复杂的例子，新旧两组子节点的顺序如下：

• 旧的子节点：p-1、p-2、p-3、p-4、p-6，p-5；
• 新的子节点：p-1、p-3、p-4、p-2、p-7、p-5；

对比发现，新的子节点多了p-7，少了节点p-6。相同的前置节点p-1，相同后置节点p-5；

接下来要进行的处理：

• 判断是否有节点需要移动，以及该如何移动
• 找出被添加或移除的节点

处理过前置节点和后置节点，索引 j 和变量newEnd和oldEnd不满足下面两个条件中的任何一个。

• j > oldEnd && j <= newEnd;
• j > newEnd && j <= oldEnd;

给函数patchKeyedChildren添加处理分支 else

function patchKeyedChildren(n1, n2, container){
  const newChildren = n2.children;
  const oldChildren = n1.children;
  // 更新相同的前置节点
  // ...
  
  // 更新相同的后置节点
  //...
  
  if(j > oldEnd && j<= newEnd){
   //...
  }else if(j > newEnd && j<= oldEnd){
    //..
  }else{
    //增加else分支，处理非理想情况
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

后续的逻辑处理将添加到else分支，首先需要构造一个source数组，长度等于新的一组子节点在经过预处理后剩余的未处理的节点的数量，并初始化source中每个元素的初始值为-1.

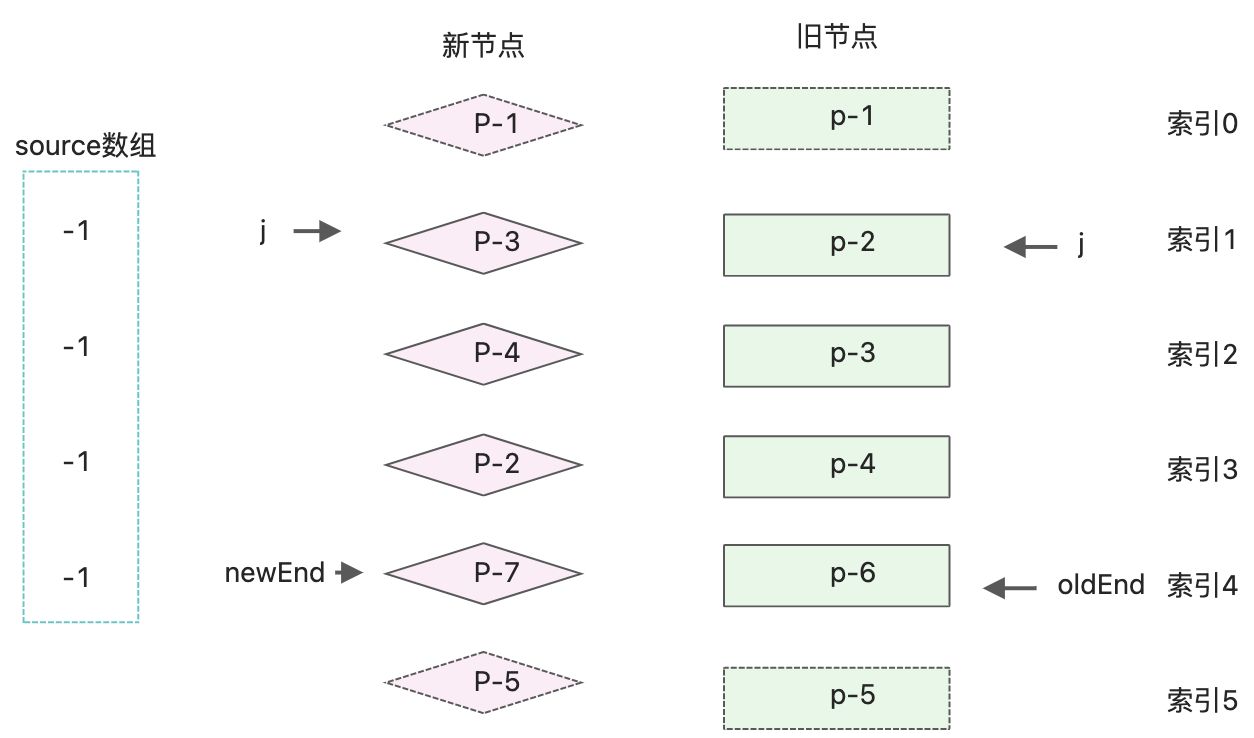
else{
  //构造source数组
  const len = newEnd - j + 1;
  const source = new Array(len);
  source.fill(-1);
}
1
2
3
4
5
6

source数组用来存储新的一组子节点中的节点在旧的一组子节点中的位置索引， 后边将会使用这个索引计算最长递增子序列，并完成DOM移动操作。

source默认初始值-1，用来存在新节点元素在旧节点中的索引值

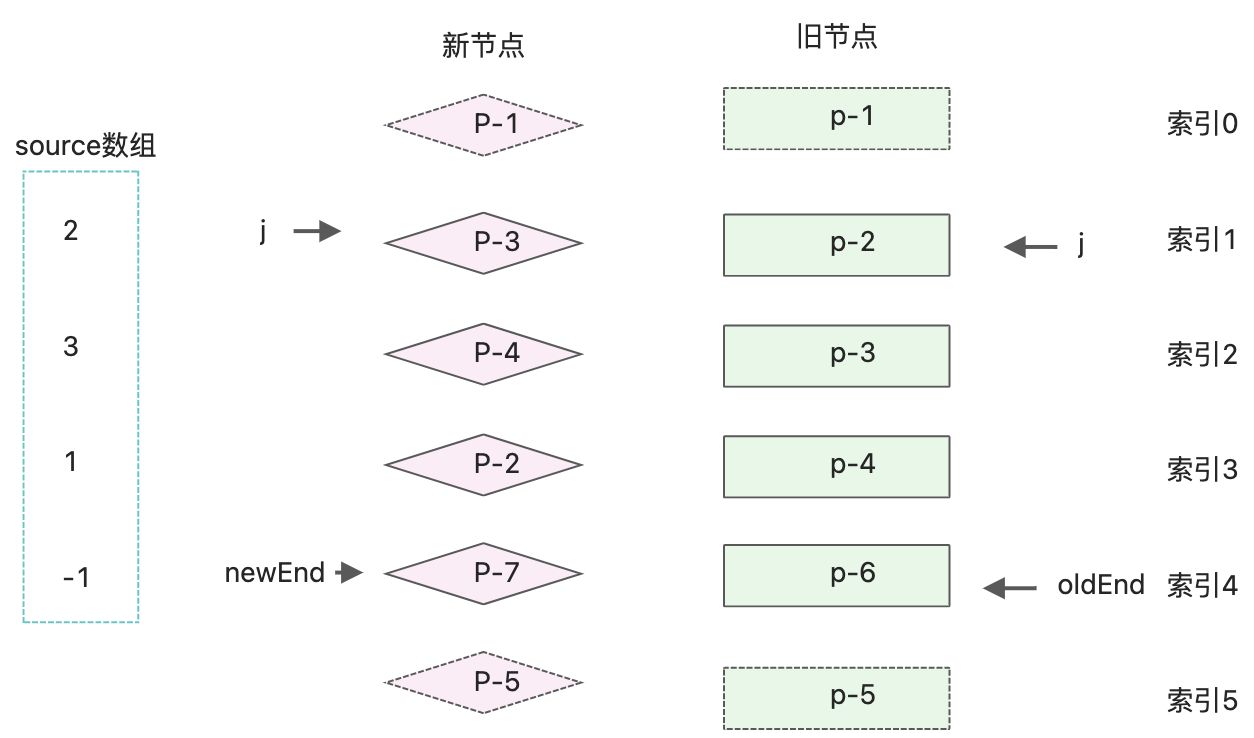
source的值为 [2, 3, 1, -1];如何用代码实现给source填充索引值，可以使用两层for循环来完成。外层循环遍历旧的子节点，内层循环遍历新的子节点；

else{
  //构造source数组
  const len = newEnd - j + 1;
  const source = new Array(len);
  source.fill(-1);
  
  // oldStart 和 newStart 分别为起始索引 j
  const oldStart = j;
  const newStart = j;
  for(let i=oldStart; i<=oldEnd; i++){
    const oldVnode = oldChildren[i];
    //
    for(let k=newStart; k<=newEnd; k++){
      const newVnode = newChildren[k];
      // 找到相同的key值
      if(oldVnode.key === newVnode.key){
        patch(oldVnode, newVnode, container)
        //填充source数组
        source[k - newStart] = i;
      }
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

source数组值填充完毕，但是目前这个方案使用了双层for循环，时间复杂度为O2

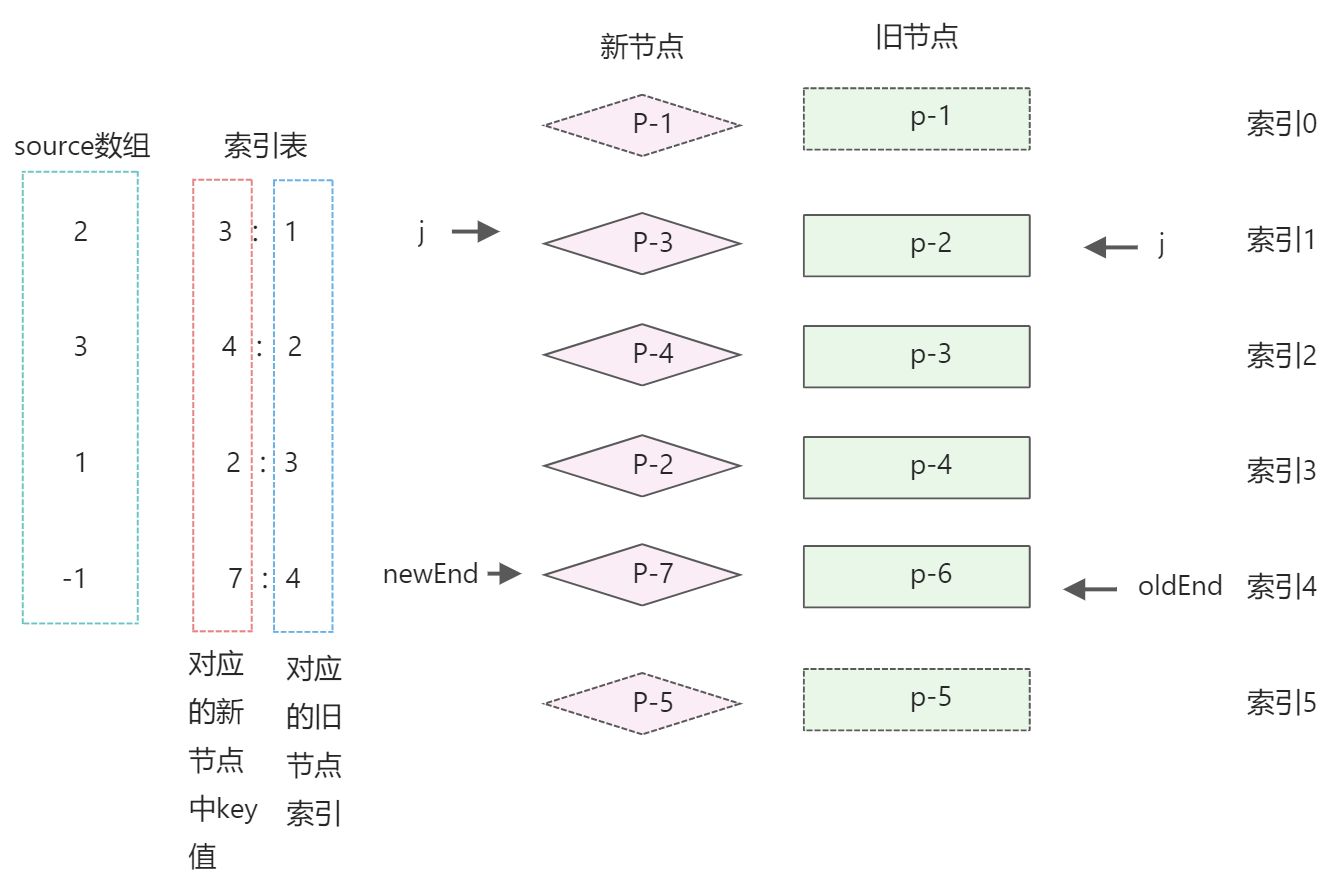
通过建立索引表，填充source值

当新旧节点数量较多时，两层for循环嵌套会带来性能问题，出于优化的目的，可以为新的一组子节点构建一张索引表，用来存储节点的key和节点位置索引之间的映射。

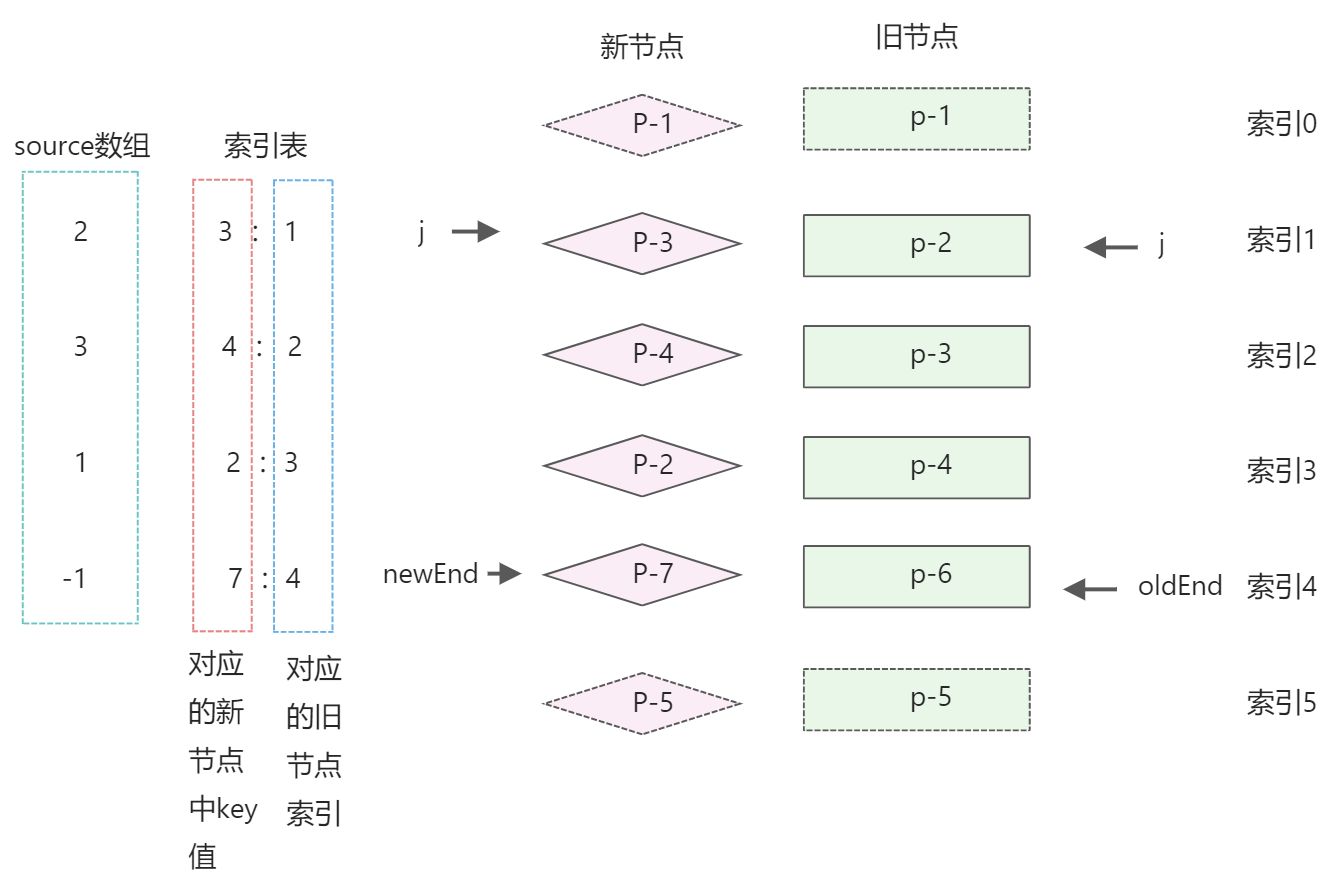
• source数组：新节点中的值，对应的值在旧节点中的索引
• 索引表： 【新节点中的key值 : 节点位置的索引】
• 第二个for循环，用来遍历旧的子节点，用旧子节点的key值去索引表keyIndx中查找该节点在新节点中的位置，并将结果存储为变量K。
  • k存在，说明节点可复用，调用patch进行打补丁，并填充source数组
  • 否则说明该节点已经不存在新的节点中，调用unmount函数卸载它

if(j > oldEnd && j <= newEnd){
  //...
}else if(j > newEnd && j<= oldEnd){
  //...
}else{
  const count = newEnd - j +1;
  const source = new Array(count);
  source.file(-1);
  
  // oldStart 和newStart 分别为起始索引
  const oldStart = j;
  const newStart = j;
  //构建索引表
  const keyIndex = {};
  for(let i = newStart; i<=newEnd; i++){
    // 以新节点的key值为key，以节点的索引序号为值
    keyIndex[newChildren[i].key] = i;
  }
  // 遍历旧的子节点中未处理的节点
  for(let i = oldStart; i<=oldEnd; i++){
    oldVnode = oldChildren[i];
    //通过旧节点中的key，在索引表中查找，相同key值的节点的位置
    const k = keyIndex[oldVnode.key];
    if(typeof k !== "undefined"){
      newVnode = newChildren[k];
      // 调用patch函数完成更新
      patch(oldVnode, newVnode, container);
      // 填充source数组
      source[k - newStart] = i;
    }else{
      unmount(oldVnode);
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

上面执行完毕，source数组已经填充。接下来判断节点是否需要移动。
新增两个变量moved和pos，moved初始值为false，表示是否需要移动节点。pos表示位置索引，初始值为0，代表遍历旧节点过程中遇到的最大索引值。如果最大索引值呈递增趋势，则不需要移动节点，否则需要移动。

if(j > oldEnd && j <= newEnd){
  //...
}else if(j > newEnd && j<= oldEnd){
  //...
}else{
  const count = newEnd - j +1;
  const source = new Array(count);
  source.file(-1);
  
  // oldStart 和newStart 分别为起始索引
  const oldStart = j;
  const newStart = j;
  // 新增变量 moved和pos
  let moved = false;
  let pos = 0;
  //构建索引表
  const keyIndex = {};
  for(let i = newStart; i<=newEnd; i++){
    // 以新节点的key值为key，以节点的索引序号为值
    keyIndex[newChildren[i].key] = i;
  }
  // 遍历旧的子节点中未处理的节点
  for(let i = oldStart; i<=oldEnd; i++){
    oldVnode = oldChildren[i];
    //通过旧节点中的key，在索引表中查找，相同key值的节点的位置
    const k = keyIndex[oldVnode.key];
    if(typeof k !== "undefined"){
      newVnode = newChildren[k];
      // 调用patch函数完成更新
      patch(oldVnode, newVnode, container);
      // 填充source数组
      source[k - newStart] = i;
      // 判断节点是否需要移动
      if(k < pos){ // k值小于pos值，说明非递增状态
        moved = false;
      } else {
        pos = k; // k大于pos，更新pos的值
      }
    }else{
      unmount(oldVnode);
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

除此之外，还需要增加一个数量表示，代表已经更新过的节点数量，如果更新过的数量超过了新子节点要更新的数量，说明存在多余的节点，应该将它们卸载。
新增patched变量，初始值为0.代表更新过节点数量。在第二个for循环中添加判断 patched <= count，则正常执行更新，每次更新都让变量patched自增；否则调用unmount函数将它们卸载。

if(j > oldEnd && j <= newEnd){
  //...
}else if(j > newEnd && j<= oldEnd){
  //...
}else{
  const count = newEnd - j +1;
  const source = new Array(count);
  source.file(-1);
  
  // oldStart 和newStart 分别为起始索引
  const oldStart = j;
  const newStart = j;
  // 新增变量 moved和pos
  let moved = false;
  let pos = 0;
  //构建索引表
  const keyIndex = {};
  for(let i = newStart; i<=newEnd; i++){
    // 以新节点的key值为key，以节点的索引序号为值
    keyIndex[newChildren[i].key] = i;
  }
  //新增patched变量，代表更新过的节点的数量
  let patched = 0;
  // 遍历旧的子节点中未处理的节点
  for(let i = oldStart; i<=oldEnd; i++){
    oldVnode = oldChildren[i];
    //如果更新过的节点数量小于等于需要更新节点数量，则执行更新
    if(patched <= count){
      //通过旧节点中的key，在索引表中查找，相同key值的节点的位置
      const k = keyIndex[oldVnode.key];
      if(typeof k !== "undefined"){
        newVnode = newChildren[k];
        // 调用patch函数完成更新
        patch(oldVnode, newVnode, container);
        // 每次更新一个节点，都将patched+1
        patched ++;
        // 填充source数组
        source[k - newStart] = i;
        // 判断节点是否需要移动
        if(k < pos){ // k值小于pos值，说明非递增状态
          moved = false;
        } else {
          pos = k; // k大于pos，更新pos的值
        }
      }else{
        unmount(oldVnode);
      }
    }else{
      // 如果更新过的节点数量大于需要更新的节点数量，需要卸载多余节点
      unmount(oldVnode);
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

代码示例

11.3如何移动元素

上一节实现的目标：

• 判断DOM是否需要DOM移动操作，创建了变量moved作为标识
• 构建source数组，数组中存储着新的子节点中的节点在旧子节点中的位置，后面根据source数组计算出最长递增子系列，用于DOM移动操作。

if(j > oldEnd && j <= newEnd){
 // ...
}else if(j > newEnd && j <= oldEnd){
 //...
}else{
  // ...
  for(let i=oldStart; i<=oldEnd; i++){
   // ...
  }
  if(moved){
    //如果moved为真，需要进行DOM移动
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13

代码新增if(moved)分支处理，如果moved为真，需要进行DOM移动，为了进行DOM移动，首先根据source数组的值计算出它的最长递增子序列。仍然使用如下图的例子

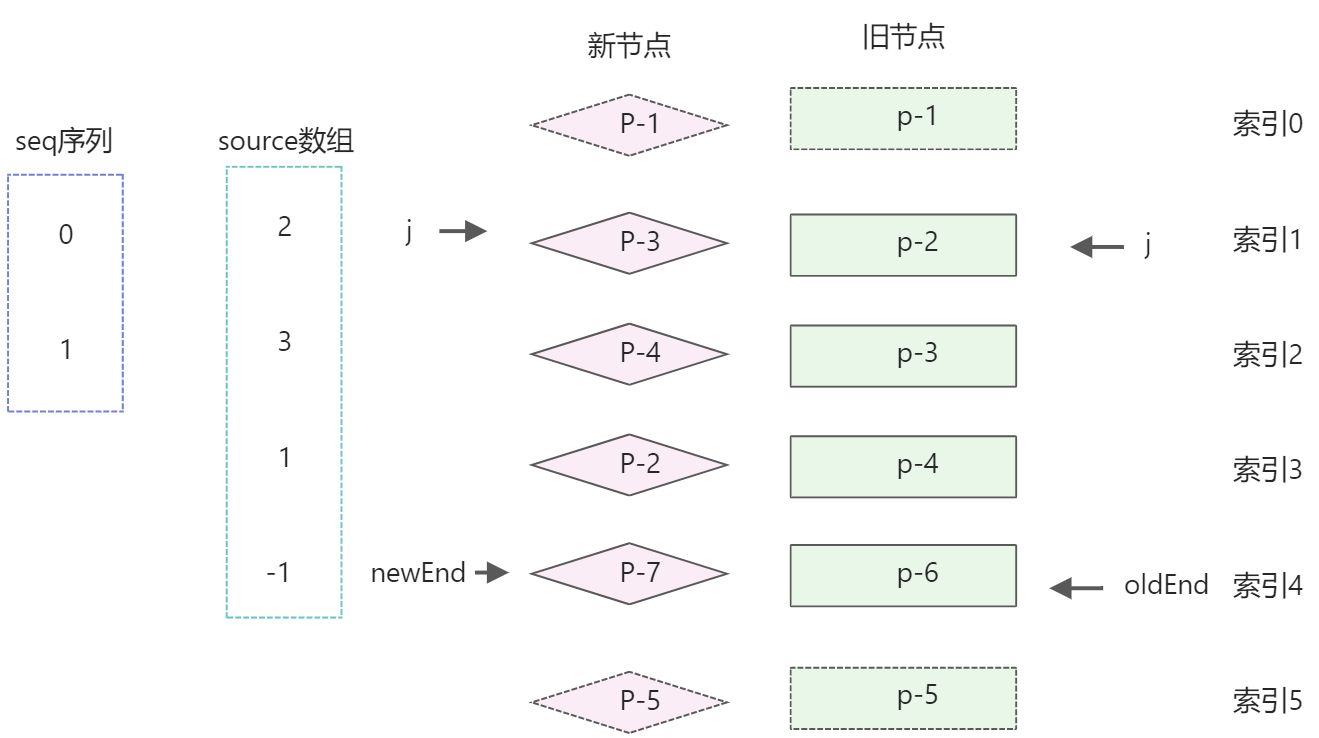
数组source的值[2, 3, 1, -1]，该数组的最长递增子序列为[0, 1];

最长递增子序列，使用lis函数计算一个数组的最长递增子序列，lis函数的返回结果是最长递增子序列中的元素在source数组中的位置索引。source的最长递增子序列是[2, 3]，最终结果是[0 ,1];
最长递增子序列的概念https://en.wikipedia.org/wiki/Longest_increasing_subsequence。具体可以查看其它详细资料。

子序列seq的值为[0,1],它的含义是，在新的子节点中，重新编码后索引值为0和1的这两个节点在更新时前后顺序没有发生变化，也就是DOM节点不用移动。0和1对应的节点为p-3和p-4。

为了完成节点移动，还要创建索引值i和s

• 用索引i指向新的子节点中的最后一个元素；i = count -1;
• 用索引s指向递增子序列中的最后一个元素 ; s = seq.length -1;

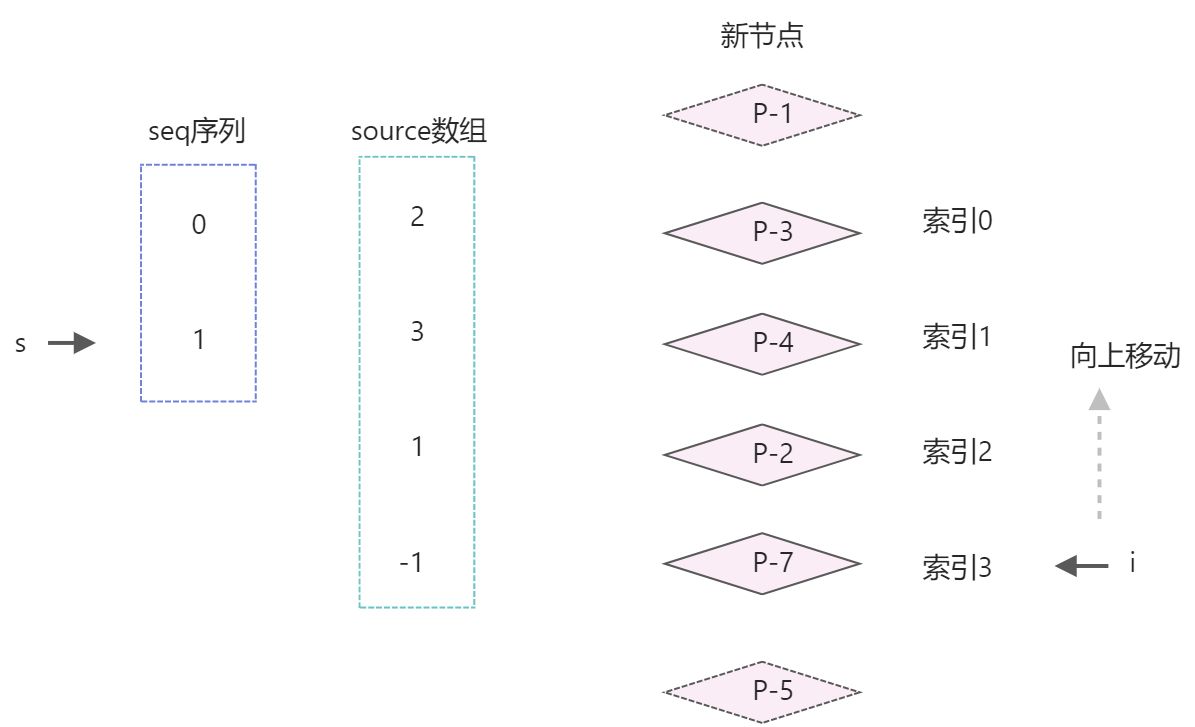
向上移动，说明for循环从后向前遍历。

if(moved){
  const seq = lis(sources);
  // s 指向最长递增子序列的最后一个元素
  let s = seq.length - 1;
  // i 指向除去前置后置元素，剩下的需要更新的节点的最后一个
  let i = count -1;
  // for循环中 i 递减，
  for(i; i>=0; i--){
    if(i !== seq[s]){
      // 如果索引i不等于 seq[s] 的值，说明节点需要移动
    }else{
      // 索引i等于seq[s]的值，节点不用移动，只要让s指向下一个位置。
      s--;
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

for循环的目的，就是让变量i向上移动，逐个访问新节点中需要更新的节点，这里的变量i就是节点的索引。
如果source[i] === -1；说明节点是全新的节点，需要进行挂载；

if(moved){
  const seq = lis(sources);
  // s 指向最长递增子序列的最后一个元素
  let s = seq.length - 1;
  // i 指向除去前置后置元素，剩下的需要更新的节点的最后一个
  let i = count -1;
  // for循环中 i 递减，
  for(i; i>=0; i--){
    if(source[i] === -1){
      //说明索引为i的节点是全新节点，该节点在children中的真实位置索引
      const pos = i + newStart
      const newVnode = newChildren[pos]
      const nextPos = pos + 1;
      // 锚点
      const anchor = nextPos < newChildren.length ? newChildren[nextPos].el : null;
      // 挂载
      patch(null, newVnode, container, anchor)
    }else if(i !== seq[s]){
      // 如果索引i不等于 seq[s] 的值，说明节点需要移动
    }else{
      // 索引i等于seq[s]的值，节点不用移动，只要让s指向下一个位置。
      s--;
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

新节点创建完毕后，for循环执行了一次。进行i–，索引i向上移动一步，指向节点p-2。
接着进入下一轮for循环

• 第一步：判断source[i]是否等于 -1 ；此时p-2节点的source的值为1，不需要重新挂载，进入下一步
• 判断 i !== seq[s] 是否成立？此时索引 i 为2，索引 s的值为1；2 !==seq[s]成立，节点p-2对应的DOM需要移动。移动后，如下图

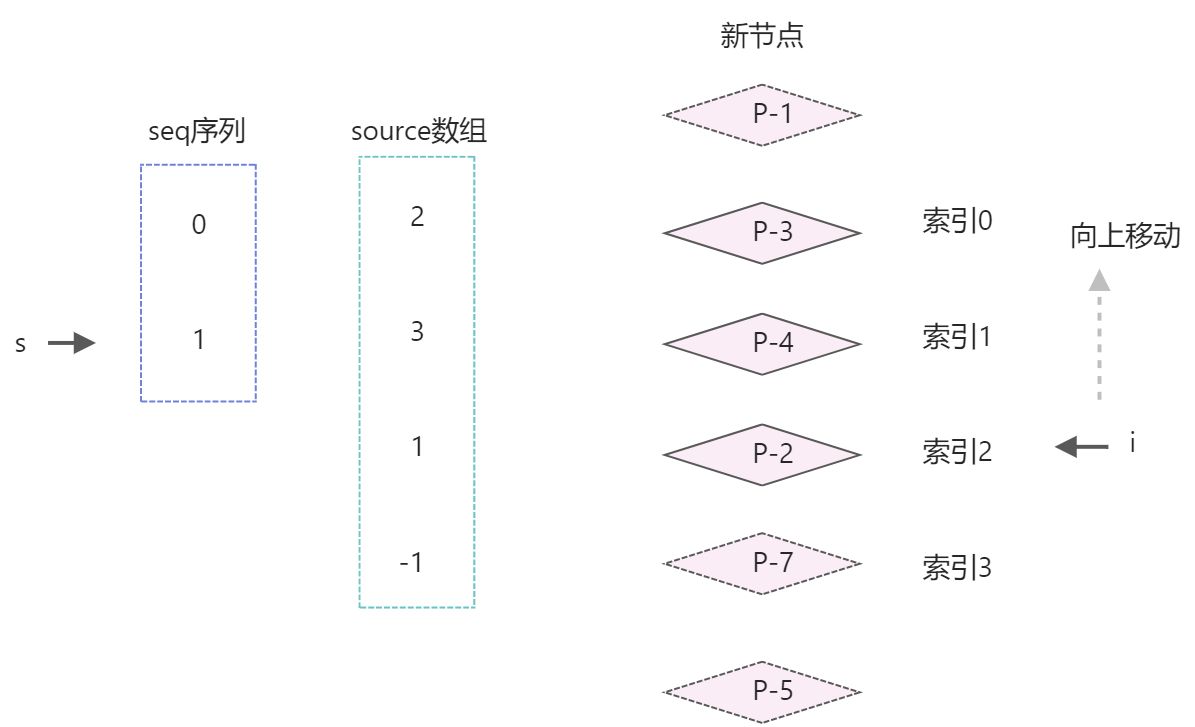
用代码实现移动p-2节点

if(moved){
  const seq = lis(sources);
  // s 指向最长递增子序列的最后一个元素
  let s = seq.length - 1;
  // i 指向除去前置后置元素，剩下的需要更新的节点的最后一个
  let i = count -1;
  // for循环中 i 递减，
  for(i; i>=0; i--){
    if(source[i] === -1){
      //说明索引为i的节点是全新节点，该节点在children中的真实位置索引
      const pos = i + newStart
      const newVnode = newChildren[pos]
      const nextPos = pos + 1;
      // 锚点
      const anchor = nextPos < newChildren.length ? newChildren[nextPos].el : null;
      // 挂载
      patch(null, newVnode, container, anchor)
    }else if(i !== seq[s]){
      // 如果索引i不等于 seq[s] 的值，说明节点需要移动
      const pos = i + newStart;
      const newVnode = newChildren[pos];
      const nextPos = pos + 1;
      //锚点
      const anchor = nextPos < newChildren.length? newChildren[nextPos].el : null;
      insert(newVnode, container, anchor);
    }else{
      // 索引i等于seq[s]的值，节点不用移动，只要让s指向下一个位置。
      s--;
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

移动节点类似挂载节点，不同点是移动节点是通过insert函数完成。
进行下一轮for循环，此时索引i指向节点p-4

更新过程分三个步骤：

• 判断source[i] === -1，条件不成立，不需要挂载节点
• 判断 i !== seq[s] ，条件不成立
• 此时 i === seq[s] , 条件成立，说明节点p-4不需要移动，只用让索引s指向s–；

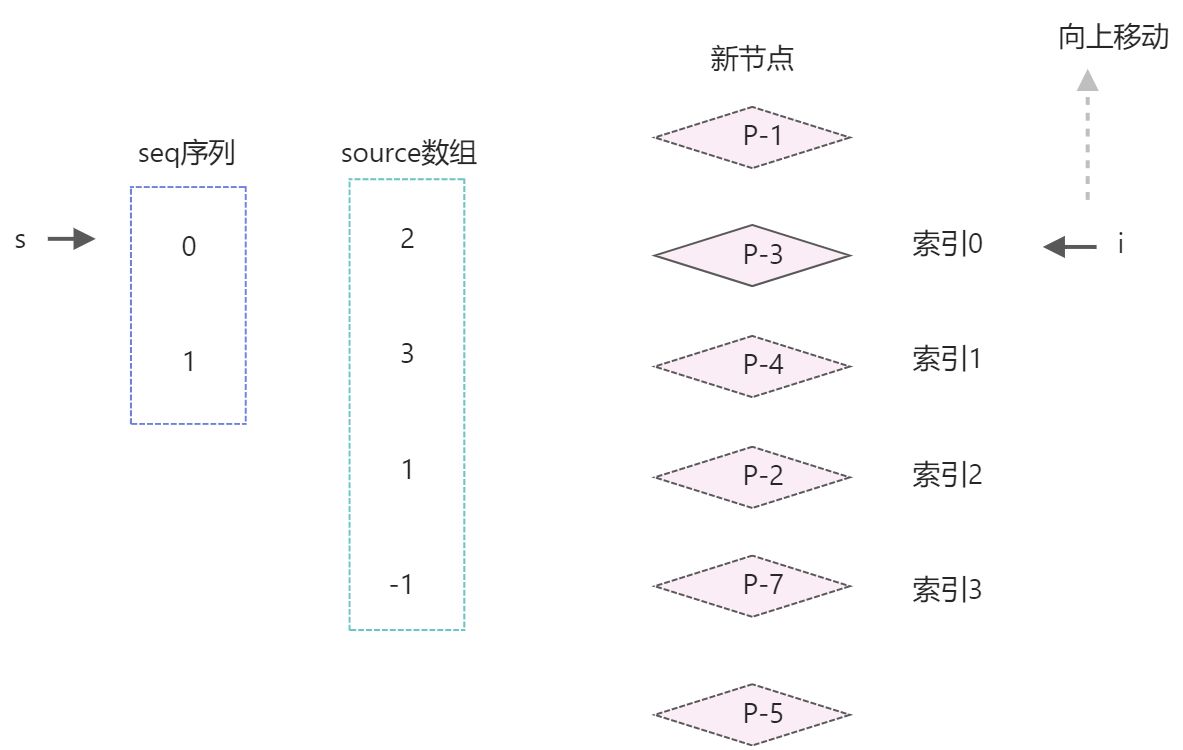
p-4节点不需要移动，进行下一轮循环。
此时索引 i 指向节点p-3，继续进行三个步骤判断：

• 判断source[i] === -1，条件不成立，不需要挂载节点
• 判断 i !== seq[s] ，条件不成立
• 此时 i === seq[s] , 条件成立，说明节点p-3不需要移动，只用让索引s指向s–；

这一轮执行完毕，循环停止，更新完成。
代码示例

vue设计与实现是本对技术讲解非常细致的书，小伙伴们可以支持下创作者。文章内容基本是书中内容，记录的没有书中详细。更详细的了解请阅读原书