【数据结构与算法】- 图（算法）

目录

1.写出从图的邻接表表示转换成邻接矩阵表示的算法。

2.[2021统考真题]已知无向连通图G由顶点集V和边集E组成，|E| > 0,当G中度为奇数的顶点个数为不大于2的偶数时，G存在包含所有边且长度为 |E| 的路径(称为EL路径)。设图G采用邻接矩阵存储，类型定义如下:

3.设计一个算法，判断一个无向图G是否为一颗树。若是一颗树，则算法返回true，否则返回false

4.写出图的深度优先搜索DFS算法的非递归算法(图采用邻接表形式)

5.分别采用基于深度优先遍历和广度优先遍历算法判别以邻接表方式存储的有向图中是否存在由顶点vi到顶点vj的路径(i != j) 。注意，算法中设计的图的基本操作必须在此存储结构上实现。

6.假设图用邻接表方式，设计一个算法，输出从顶点vi到顶点vj的所有简单路径。

7.试着说明利用dfs如何实现有向无环图拓扑排序。

---

1.写出从图的邻接表表示转换成邻接矩阵表示的算法。

//写出从图的邻接表表示转换成邻接矩阵表示的算法
#include<iostream>
using namespace std;
 
//邻接表存储结构
//边表的节点
typedef struct Arcnode{
    //当前弧指向顶点的位置
	int adjvex;
	//指向下一条弧的指针
	struct Arcnode *next;
}Arcnode;
 
//顶点表节点
typedef struct Vnode{
    //顶点信息
	char data;
	//指向第一条依附该顶点的弧的指针
	Arcnode *first;
}Vnode,AdjList[10];
 
//组合的邻接表
typedef struct{
    //邻接表
	AdjList v;
	//顶点数和弧数
	int vnum,arcnum;
}ALGraph;
 
//转换函数
void Convert(ALGraph &G,int arcs[M][N])
{
	//用来取边
	Arcnode *p;
	//遍历每条顶点表节点为头的边链表
	for(int i=0;i<n;i++)
	{
		//取顶点i的第一个出边
		p = (G.v[i]).first;
 
		//遍历该顶点表节点为头的边链表
		while(p!=NULL)
		{
			//置1
			arcs[i][p->adjvex]=1;
			//指向下一个节点 即取下一条边
			p=p->next;
		}
	}
}
 
int main()
{
	return 0;
}

2.[2021统考真题]已知无向连通图G由顶点集V和边集E组成，|E| > 0,当G中度为奇数的顶点个数为不大于2的偶数时，G存在包含所有边且长度为 |E| 的路径(称为EL路径)。设图G采用邻接矩阵存储，类型定义如下:

请设计算法int IsExistEL(MGraph G)， 判断G是否存在EL路径，若存在，则返回1，否则返回0。

//判断图是否有EL路径
#include<iostream>
using namespace std;
 
//邻接矩阵存储的结构体
typedef struct{
   int numVertices,numEdges;
   char VerticesList[6];
   int Edge[6][6];
}MGraph;
 
int IsExistEL(MGraph G)
{
	//度数和结果变量
	int degree,count=0;
	//遍历邻接矩阵 依次遍历每一行
	for(int i=0;i<G.numVertices;i++)
	{
		//每一行度数初始化为0
		degree =0;
		//遍历该行
		for(int j=0;j<G.numVertices;j++)
		{
			//度数增加
			degree+=G.Edge[i][j];
		}
		//奇数+1
		if(degree%2!=0) count++;
	}
	//0或者2 就是存在
	if(count==0||count==2) return 1;
	//否则不存在
	return 0;
}
 
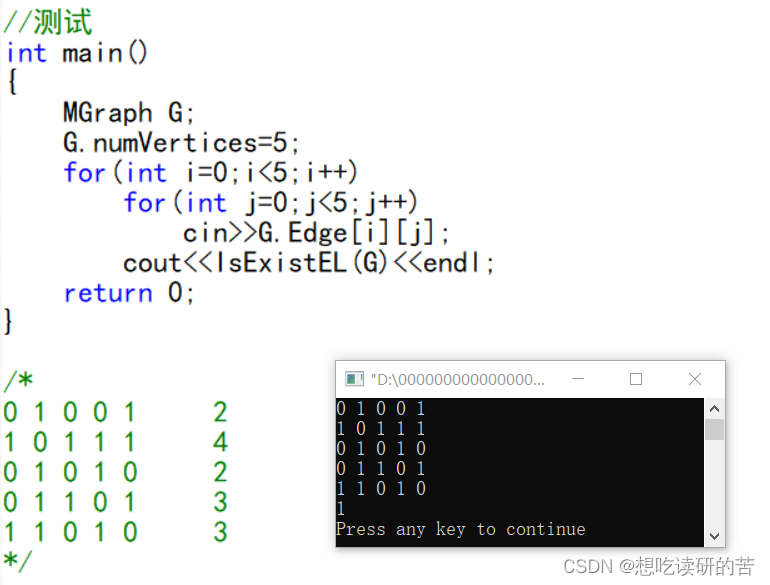
//测试
int main()
{
	MGraph G;
	G.numVertices=5;
	for(int i=0;i<5;i++)
		for(int j=0;j<5;j++)
			cin>>G.Edge[i][j];
		cout<<IsExistEL(G)<<endl;
	return 0;
}
 
/*
0 1 0 0 1     2
1 0 1 1 1     4
0 1 0 1 0     2
0 1 1 0 1     3
1 1 0 1 0     3
*/

3.设计一个算法，判断一个无向图G是否为一颗树。若是一颗树，则算法返回true，否则返回false

//设计一个算法判断 一个无向图G是否为一颗树 
//若是一颗树 则算法返回true 否则返回false
 
//DFS
void DFS(Graph &G,int v,int &Vnum,int &Enum,int visited[])
{
	visited[v]=true;//访问过
	Vnum++;//顶点数+1
	int w=FirstNeighbor(G,v);
	while(w!=-1)
	{
		//第一个邻接节点存在 存在边
		Enum++;//边+1
		if(!visited[w])//该邻接点有没有访问过
			DFS(G,W,Vnum,Enum,visited);//继续遍历
		w=NextNeighbor(G,v,w);  //找下一个邻接点
	}
}
 
//判断是否是树
bool istree()
{
	//顶点数 边数
	int Vnum=0,Enum=0;
	//访问标记数组
	bool visited[Max];
	for(int i=0;i<Max;i++)
	{
		visited[i]=false;
	}
	DFS(G,1,Vnum,Enum,visited);
	if(Vnum==G.vexnum&&Enum==2*(G.vexnum-1))
		return true;
	return false;
}

4.写出图的深度优先搜索DFS算法的非递归算法(图采用邻接表形式)

//写出图的深度优先搜索DFS算法的非递归算法（图采用邻接表形式）
 
//非递归深度优先搜索
void DFS(AGraph &G,int v)
{
	//初始化栈
	stack S;
	InitStack(S);
	//初始化visited数组
	bool visited[G.vexnum+1];
	for(int i=0;i<G.vexnum;i++) visited[i]=false;
	//顶点压入栈中
	Push(S,v);
	visited[v]=true;
	//顶点已经被压入过，更新visited数据
	//退栈
	while(!Isempty(S))
	{
		k=Pop(S);
		//访问该节点 访问的顺序就是DFS顺序
		visit(k);
		//访问所有的邻接节点
		for(w=FirstNeighbor(G,k);w>=0;w=NextNeighbor(G,k,w))
		{
			//没有进过栈的话进栈
			if(!visited[w])
			{
				Push(S,w);
				visited[w]=true;
			}
		}
	}
}

5.分别采用基于深度优先遍历和广度优先遍历算法判别以邻接表方式存储的有向图中是否存在由顶点vi到顶点vj的路径(i != j) 。注意，算法中设计的图的基本操作必须在此存储结构上实现。

//分别采用基于深度优先遍历和广度优先遍历算法判别以
//邻接表方式存储的有向图中是否存在由顶点vi到顶点vj的路径(i!=j)
 
//visited数组
int visited[Max];
 
//DFS
void DFS(ALGraph G,int i,int j,bool &isok)
{
	//如果当前节点就是j节点
	if(i==j)
	{
	   //isok赋值 并退出函数
		isok=true;
		return;
	}
	//否则更新访问标记
	visited[i]=1;
	//遍历邻接点 向后延申
	for(int p=FirstNeighbor(G,i);p>=0;p=NextNeighbor(G,i,p))
	{
		//没有找到j点并且该点没有访问过 继续DFS遍历
		if(!visited[p]&&!isok)  DFS(G,p,j,isok);
	}
}
 
//BFS
int BFS(ALGraph G,int i,int j)
{
	//初始化队
	InitQueue(Q);
	//顶点入队
	EnQueue(Q,i);
	//循环体 遍历队
	while(!isempty(Q))
	{
    //出队 保留出队元素
		Dequeue(Q,u);
	//更新访问标记
		visited[u]=1;
	//如果当前点为j 即返回
		if(u==j) return 1;
	//否则遍历邻接点
	    for(int p=FirstNeighbor(G,i);p>=0;p=NextNeighbor(G,i,p))
		{
			//再次判断是否为j点
			if(p==j) return 1;
	        //是的话返回
	        //不是 将邻接点入队
			if(!visited[p])
			{
				Enqueue(Q,p);
				visited[p]=1;
				//更新访问标记
			}
		}
	}
	return 0;
}

6.假设图用邻接表方式，设计一个算法，输出从顶点vi到顶点vj的所有简单路径。

//假设图用邻接表表示 设计一个算法 输出从顶点vi到vj的所有简单路径
 
void FindPath(AGraph *G,int u,int v,int path[],int d)
{
	//添加当前节点到路径当中 首先路径要+1 再加入节点
	d++;
	path[d]=u;
	//这时候当前节点访问过
	visited[u]=1;
	//如果该点为路径终点 就输出
	if(u==v) cout<<path<<endl;
	//指向u的邻接点 即第一个相邻点
	ArcNode *p=G->adjlist[u].firstarc;
	//不断去访问相邻点的下一个相邻点 往深处去搜索
	while(p!=NULL)
	{
		//获取当前的邻接点的弧所指向顶点的位置
		int w=p->adjvex;
		//如果这个点没有访问过 递归的去往下找
		if(visited[w]==0)
			FindPath(G,w,v,path,d);
		//之后p后移
		p=p->nextarc;
	}
	//为了该点可以重新使用 visit=0
	visited[u]=0;
}

7.试着说明利用dfs如何实现有向无环图拓扑排序。

//试着说明利用DFS如何实现有向无环图拓扑排序
 
int finishtime[Max];
//访问的标记数组
bool visited[Max];
 
void DFS(Graph G,int v)
{
	//访问当前节点
	visited[v]=true;
	visit(v);
	//深度遍历邻接节点
	for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w))
	{
		if(!visited[w]) DFS(G,w);
	}
	//时间存储
	time++;
	finishtime[v]=time;
}
 
void DFSTraverse(Graph G)
{
	//初始化标记数组
	for(int i=0;i<G.vexnum;i++)
	{
		visited[i]=false;
	}
	//初始化时间
	time = 0;
	//dfs每个没有被访问过的节点
	for(int v=0;v<G.vexnum;i++)
	{
		if(!visited[v]) DFS(G,v);
	}
}