目录

1.概念

2.例子

3.线性回归经常使⽤的两种优化算法

3.0背景（损失函数）

3.1正规⽅程

3.2梯度下降

 3.3两个方法对比

4.岭回归

 5.模型的保存和加载

1.概念

 

线性回归(Linear regression)是利⽤回归⽅程(函数)对⼀个或多个⾃变量(特征值)和因变量(⽬标值)之间关系进⾏建模的 ⼀种分析⽅式。

理解为： 1.期末成绩：0.7×考试成绩+0.3×平时成绩

2.房⼦价格 = 0.02×中⼼区域的距离 + 0.04×城市⼀氧化氮浓度 + (-0.12×⾃住房平均房价) + 0.254×城镇犯罪率

2.例子

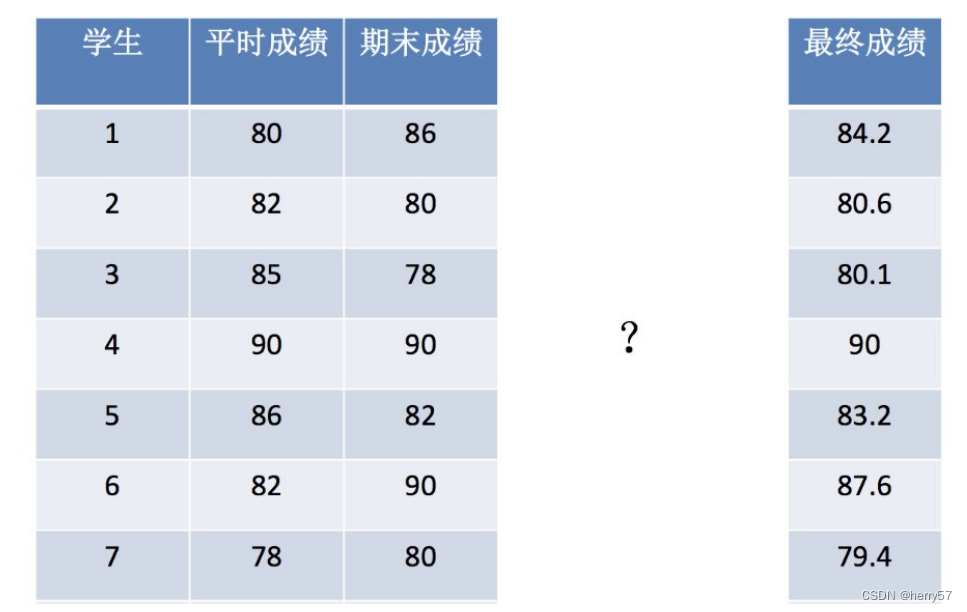
from sklearn.linear_model import LinearRegression
 
x = [[80, 86],
[82, 80],
[85, 78],
[90, 90],
[86, 82],
[82, 90],
[78, 80],
[92, 94]]
#第一列平均成绩，第二列期末成绩
y = [84.2, 80.6, 80.1, 90, 83.2, 87.6, 79.4, 93.4]
# 实例化API
estimator = LinearRegression()
# 使⽤fit⽅法进⾏训练
estimator.fit(x,y)
prediction=estimator.predict([[100, 80]])
print(prediction)
print(estimator.coef_)

3.线性回归经常使⽤的两种优化算法

3.0背景（损失函数）

 y 为第i个训练样本的真实值  h(x )为第i个训练样本特征值组合预测函数

⼜称最⼩⼆乘法，求损失函数最小值

3.1正规⽅程

理解：X为特征值矩阵，y为⽬标值矩阵。直接求到最好的结果

缺点：当特征过多过复杂时，求解速度太慢并且得不到结果

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
 
 
# 1.获取数据
data = load_boston()
# 2.数据集划分
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22) #数据划分默认0.25
# 3.特征⼯程-标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)
# 4.机器学习-线性回归(正规⽅程)
estimator = LinearRegression()
estimator.fit(x_train, y_train)
# 5.模型评估
# 5.1 获取系数等值
y_predict = estimator.predict(x_test)
print("预测值为:\n", y_predict)
print("模型中的系数为:\n", estimator.coef_)
print("模型中的偏置为:\n", estimator.intercept_)
# 5.2 评价
# 均⽅误差
error = mean_squared_error(y_test, y_predict)
print("误差为:\n", error)

3.2梯度下降

 1.α在梯度下降算法中被称作为学习率或者步⻓，意味着我们可以通过α来控制每⼀步⾛的距离，走太快，错过最低点，走太慢，效率慢

2.梯度的⽅向实际就是函数在此点上升最快的 ⽅向！⽽我们需要朝着下降最快的⽅向⾛，⾃然就是负的梯度的⽅向

 公式步骤演示：我们假设有⼀个单变量的函数 :J(θ) = θ 函数的微分:J (θ) = 2θ 初始化，起点为： θ = 1 学习率：α = 0.4

 如图，经过四次的运算，也就是⾛了四步，基本就抵达了函数的最低点，也就是⼭底

 3.3两个方法对比

梯度下降法和正规⽅程选择依据

⼩规模数据： 正规⽅程：LinearRegression(不能解决拟合问题)

                        岭回归

⼤规模数据： 梯度下降法：SGDRegressor 

4.岭回归

from sklearn.linear_model import Ridge,RidgeCV
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
 
 
# 1.获取数据
data = load_boston()
# 2.数据集划分
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22) #数据划分默认0.25
# 3.特征⼯程-标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)
# 4.机器学习-线性回归(岭回归)
estimator = Ridge(alpha=1) #alpha为正则化
# estimator = RidgeCV(alphas=(0.1, 1, 10))
estimator.fit(x_train, y_train)
# 5.模型评估
# 5.1 获取系数等值
y_predict = estimator.predict(x_test)
print("预测值为:\n", y_predict)
print("模型中的系数为:\n", estimator.coef_)
print("模型中的偏置为:\n", estimator.intercept_)
# 5.2 评价
# 均⽅误差
error = mean_squared_error(y_test, y_predict)
print("误差为:\n", error)

 5.模型的保存和加载

from sklearn.linear_model import Ridge,RidgeCV
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import joblib
 
# 1.获取数据
data = load_boston()
# 2.数据集划分
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22) #数据划分默认0.25
# 3.特征⼯程-标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)
# 4.机器学习-线性回归(岭回归)
# #4.1模型训练
# estimator = Ridge(alpha=1) #alpha为正则化
# # estimator = RidgeCV(alphas=(0.1, 1, 10))
# estimator.fit(x_train, y_train)
# #4.2模型保存
# joblib.dump(estimator,"./machineLearnCode/LinearRegressionTest/test.pkl")
#4.3模型加载
estimator=joblib.load("./machineLearnCode/LinearRegressionTest/test.pkl")
 
# 5.模型评估
# 5.1 获取系数等值
y_predict = estimator.predict(x_test)
print("预测值为:\n", y_predict)
print("模型中的系数为:\n", estimator.coef_)
print("模型中的偏置为:\n", estimator.intercept_)
# 5.2 评价
# 均⽅误差
error = mean_squared_error(y_test, y_predict)
print("误差为:\n", error)