-
(树) 树状数组
前言
说到树型结构，最大的优势就是能让 O ( n ) {O(n)} O(n)的一些操作化简到 O ( l o g n ) {O(logn)} O(logn)
而本文的主题“树状数组”自然也不例外
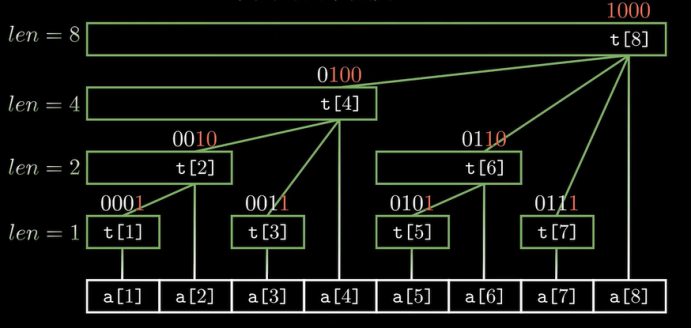
树状数组运用二进制中1的个数和关系，让大数保存小数的数值。
但是由于线段树的光环太大了，树状数组的讨论度太低了，但还是有必要了解一下的
本题不从0开始讲解，主要是模板的展示和使用
注意： 树状数组的下标是从1开始的（1~n）
相关讲解
〔manim | 算法 | 数据结构〕 完全理解并深入应用树状数组 | 支持多种动态维护区间操作
lowbit()
讲解：2的幂 - 力扣官方题解
直接发现规律其实比较困难
从相邻大数和小数看紧密的关系在于末尾的1的区别，因此我们就需要快速获取末尾的1
就需要lowbit()函数，具体原理自行模拟就能理解 (位运算性质的功底)
练习题
洛谷：P3374 【模板】树状数组 1 单点修改，区间查询
洛谷：P3368 【模板】树状数组 2 区间修改， 单点查询
杭电：敌兵布阵 - 1166
经典问题：(逆序对总数) 离散化+树状数组
实现与应用
核心函数
// 下标 [1, n] class TreeArray { private: int n; vector<int> tree; inline int lowbit(int x) { return x & (-x); } public: TreeArray() {} TreeArray(int n) : n(n), tree(n + 1) {} void add(int i, int val) { for (; i <= n; i += lowbit(i)) { tree[i] += val; } } int ask(int i) { int sum = 0; for (; i > 0; i -= lowbit(i)) { sum += tree[i]; } return sum; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
延伸应用
// 单点修改，查询前缀和 add(x, val); ans = ask(x); // 单点修改，单点查询 add(x, val); ans = ask(x) - ask(x - 1); // 单点修改，区间查询 add(x, val); ans = ask(r) - ask(l - 1); //右-（左-1） /** ************************************************************/ // 区间修改，单点查询 （此处用差分数组） add(l, val); add(r + 1, -val); ans = arr[x] + ask(x); // arr表示原始数据，ask记录的是差分 /** ************************************************************/ // 区间修改，区间查询 // 代码较长，直接见下方示例- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
例题代码
单点修改 区间查询
// P3374 【模板】树状数组 1 #include <bits/stdc++.h> using namespace std; class TreeArray { private: int n; vector<int> tree; public: TreeArray() {} TreeArray(int n) : n(n), tree(n + 1) {} inline int lowbit(int x) { return x & (-x); } void add(int i, int val) { for (; i <= n; i += lowbit(i)) { tree[i] += val; } } int ask(int i) { int sum = 0; for (; i > 0; i -= lowbit(i)) { sum += tree[i]; } return sum; } }; int main() { int n, m; cin >> n >> m; TreeArray tarr(n); for (int i = 1, val; i <= n; i++) { cin >> val; tarr.add(i, val); } while (m--) { int inquire; cin >> inquire; if (inquire == 1) { int pos, val; cin >> pos >> val; tarr.add(pos, val); } else { int left, right; cin >> left >> right; int ans = tarr.ask(right) - tarr.ask(left - 1); cout << ans << endl; } } return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
区间修改 单点查询
// P3368 【模板】树状数组 2 // 树状数组存储的是变化值 #include <bits/stdc++.h> using namespace std; class TreeArray { private: int n; vector<int> arr; // 存储原始数据值 vector<int> tree; // 存储差分值 public: TreeArray() {} TreeArray(int n) : n(n), tree(n + 1) {} TreeArray(int n, vector<int>& arr) : n(n), tree(n + 1), arr(arr) {} inline int lowbit(int x) { return x & (-x); } void add(int i, int val) { for (; i <= n; i += lowbit(i)) { tree[i] += val; } } int ask(int i) { int sum = 0; for (; i > 0; i -= lowbit(i)) { sum += tree[i]; } return sum; } int query(int i) { return arr[i] + ask(i); } }; int main() { int n, m; cin >> n >> m; vector<int> arr(n + 1); for (int i = 1; i <= n; i++) { cin >> arr[i]; } TreeArray tarr(n, arr); while (m--) { int inquire; cin >> inquire; if (inquire == 1) { int left, right, val; cin >> left >> right >> val; tarr.add(left, val); // 左 + tarr.add(right + 1, -val); // 右+1 - } else { int x; cin >> x; cout << tarr.query(x) << endl; } } return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
区间修改 区间查询
需要定义两个数组，是通过数学推导出来的，光看文字比较难理解，死记就行了
练习题：
由于没找到适合的简单题就用了这道题，想要完成这题需要会树链剖分
但本文的学习重点放在下面的工具模板类
TreeArray的实现和调用即可
本题大致流程：
- 用树链剖分获得递归序列 idx[] 下标 和 newVal[] 对应的点权
- 用新点权初始化树状数组 (手动循环初始化)
- 利用树链剖分的lca操作，查询和更新
- 注意：由于会出现减法和负数，在取模的时要注意
// P3384 【模板】轻重链剖分/树链剖分 // 树链剖分 + 树状数组 (线段树也行) #include <bits/stdc++.h> #define int long long using namespace std; const int M = 10 + 1 * 100000; static int mod = 1e9 + 7; // 随意赋值，题目要求手动输入 /** ******************************************************************/ vector<int> oldVal(M); // 点权的初始值 vector<int> newVal(M); // 剖分后对应的值 /** ******************************************************************/ // 树状数组 // 区间修改 区间查询 class TreeArray { private: int n; vector<int> tree1; vector<int> tree2; inline int lowbit(int x) { return x & (-x); } void updata(int i, int val) { for (int p = i; i <= n; i += lowbit(i)) { tree1[i] += val; tree2[i] += p * val; // 注意负数取模 tree1[i] %= mod; tree1[i] = (tree1[i] + mod) % mod; tree2[i] %= mod; tree2[i] = (tree2[i] + mod) % mod; } } int query(int i) { int sum = 0; for (int p = i; i > 0; i -= lowbit(i)) { sum += (p + 1) * tree1[i] - tree2[i]; sum %= mod; sum = (sum + mod) % mod; } return sum; } public: TreeArray() {} TreeArray(int n) : n(n), tree1(n + 1), tree2(n + 1) {} // 区间修改 void rangeUpdata(int left, int right, int val) { updata(left, val); updata(right + 1, -val); } // 区间查询 int rangeQuery(int left, int right) { return (query(right) - query(left - 1) + mod) % mod; } }; TreeArray tarr; // 全局对象，便于lca调用 /** ******************************************************************/ // 树链剖分模板 vector<vector<int>> graph(M); // 图 vector<int> father(M); // 父节点 vector<int> son(M); // 重孩子 vector<int> size(M); // 子树节点个数 vector<int> deep(M); // 深度，根节点为1 vector<int> top(M); // 重链的头，祖宗 vector<int> idx(M); // 剖分新idx int cnt = 0; // 剖分计数 void dfs1(int cur, int from) { deep[cur] = deep[from] + 1; // 深度，从来向转化来 father[cur] = from; // 父节点，记录来向 size[cur] = 1; // 子树的节点数量 son[cur] = 0; // 重孩子 (先默认0表示无) for (int& to : graph[cur]) { if (to == from) { // 避免环 continue; } dfs1(to, cur); // 处理子节点 size[cur] += size[to]; // 节点数量叠加 if (size[son[cur]] < size[to]) { // 松弛操作，更新重孩子 son[cur] = to; } } } void dfs2(int cur, int grandfather) { top[cur] = grandfather; // top记录祖先 idx[cur] = ++cnt; // 记录剖分idx newVal[cnt] = oldVal[cur]; // 映射到新值 if (son[cur] != 0) { // 优先dfs重儿子 dfs2(son[cur], grandfather); } for (int& to : graph[cur]) { if (to == father[cur] || to == son[cur]) { continue; // 不是cur的父节点，不是重孩子 } dfs2(to, to); // dfs轻孩子 } } // lca模板 本题中未使用 int lca(int x, int y) { while (top[x] != top[y]) { // 直到top祖宗想等 if (deep[top[x]] < deep[top[y]]) { swap(x, y); // 比较top祖先的深度，x始终设定为更深的 } x = father[top[x]]; // 直接跳到top的父节点 } return deep[x] < deep[y] ? x : y; // 在同一个重链中，深度更小的则为祖宗 } /** ******************************************************************/ void updatePath(int x, int y, int val) { while (top[x] != top[y]) { if (deep[top[x]] < deep[top[y]]) { swap(x, y); } tarr.rangeUpdata(idx[top[x]], idx[x], val); x = father[top[x]]; } if (deep[x] < deep[y]) { swap(x, y); } tarr.rangeUpdata(idx[y], idx[x], val); } void updateTree(int root, int val) { tarr.rangeUpdata(idx[root], idx[root] + size[root] - 1, val); } int queryPath(int x, int y) { int sum = 0; while (top[x] != top[y]) { if (deep[top[x]] < deep[top[y]]) { swap(x, y); } sum += tarr.rangeQuery(idx[top[x]], idx[x]); sum %= mod; x = father[top[x]]; } if (deep[x] < deep[y]) { swap(x, y); } sum += tarr.rangeQuery(idx[y], idx[x]); return sum % mod; } int queryTree(int root) { return tarr.rangeQuery(idx[root], idx[root] + size[root] - 1); } /** ******************************************************************/ signed main() { int n, m, root; cin >> n >> m >> root >> mod; for (int i = 1; i <= n; i++) { cin >> oldVal[i]; } // 该树编号 [1, n] // 本题仅仅说有边，未说方向 for (int i = 1, u, v; i <= n - 1; i++) { cin >> u >> v; graph[v].emplace_back(u); graph[u].emplace_back(v); } // 树链剖分 重链 dfs1(root, 0); dfs2(root, root); // 根据映射的newVal建树 tarr = TreeArray(n); // 区间修改 区间查询 需要手动初始化 for (int i = 1; i <= n; i++) { tarr.rangeUpdata(i, i, newVal[i]); } for (int i = 1, ask; i <= m; i++) { cin >> ask; int from, to, val, subtree; if (ask == 1) { cin >> from >> to >> val; updatePath(from, to, val); } else if (ask == 2) { cin >> from >> to; cout << queryPath(from, to) % mod << endl; } else if (ask == 3) { cin >> subtree >> val; updateTree(subtree, val); } else { cin >> subtree; cout << queryTree(subtree) % mod << endl; } } return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
经典应用 逆序对总数
离散化：(化简复杂度) 离散化_天赐细莲的博客-CSDN博客_离散化时间复杂度
官方题解中写的离散化简洁很多
// 下标 [1, n] class TreeArray { private: int n; vector<int> tree; inline int lowbit(int x) { return x & (-x); } public: TreeArray() {} TreeArray(int n) : n(n), tree(n + 1) {} void add(int i, int val) { for (; i <= n; i += lowbit(i)) { tree[i] += val; } } int ask(int i) { int sum = 0; for (; i > 0; i -= lowbit(i)) { sum += tree[i]; } return sum; } }; class Solution { public: int reversePairs(vector<int>& nums) { int n = nums.size(); if (n < 2) { return 0; } // 获得离散化的数组 vector<int> arr = toDiscretization(nums); TreeArray ta(n); int ans = 0; for (int i = 0; i < n; i++) { int cur = arr[i]; // 从已经记录的比当前值大的求和，但不能包括自身 ans += ta.ask(n) - ta.ask(cur); // 加入树状数组，为后续操作服务 ta.add(cur, 1); } return ans; } private: // 需要考虑相同值，考虑树状数组规定下标从1开始 vector<int> toDiscretization(vector<int>& arr, int idx = 1) { int n = arr.size(); if (n == 0) { return {}; } multimap<int, int> mmp; for (int i = 0; i < n; i++) { mmp.insert({arr[i], i}); } vector<int> discretization(n); auto it = mmp.begin(); int pre = it->first; discretization[it->second] = idx; for (it++; it != mmp.end(); it++) { int cur = it->first; int i = it->second; if (cur == pre) { discretization[i] = idx; } else { discretization[i] = (++idx); } pre = cur; } return discretization; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
END
-
相关阅读:
【面试经典150 | 双指针】三数之和
2023年09月 C/C++（二级）真题解析#中国电子学会#全国青少年软件编程等级考试
Drools实战
编程的终结；展望2023年AI系统方向；AI的下一个阶段
Spring Security（6）
基于ASP.net的服装商城设计
mysql 创建索引
邦芒宝典：工作中如何自我定位
横向柱状图数据配置
超标量处理器设计 姚永斌 第4章 分支预测 --4.1 小节摘录
- 原文地址：https://blog.csdn.net/CUBE_lotus/article/details/125430922