cartographer_optimization_problem_2d

0.引言

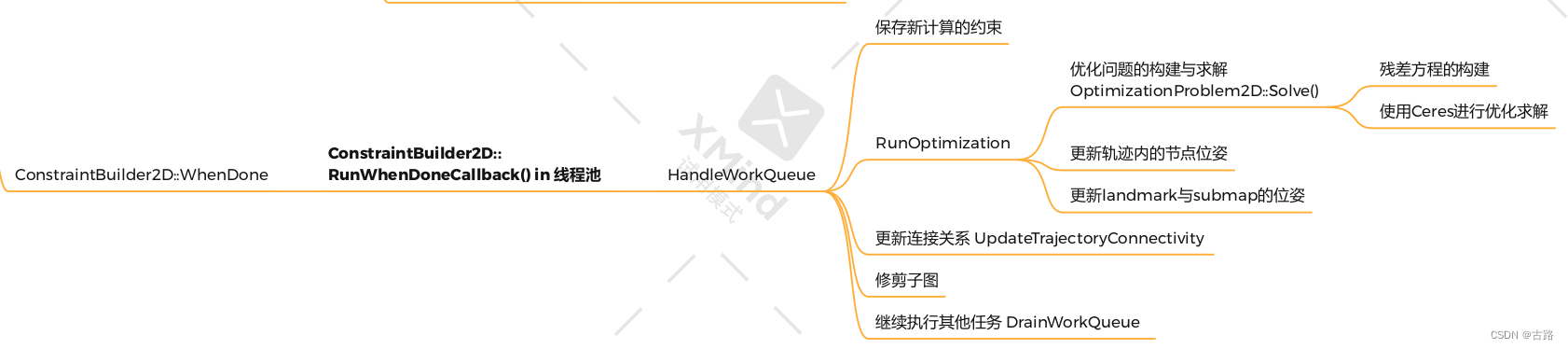
主要业务逻辑回到mapping/internal/2d/pose_graph_2d.cc/PoseGraph2D::HandleWorkQueue-->RunOptimization()中。具体的优化这一部分就是在optimization中进行实现。

前面计算约束结果为：

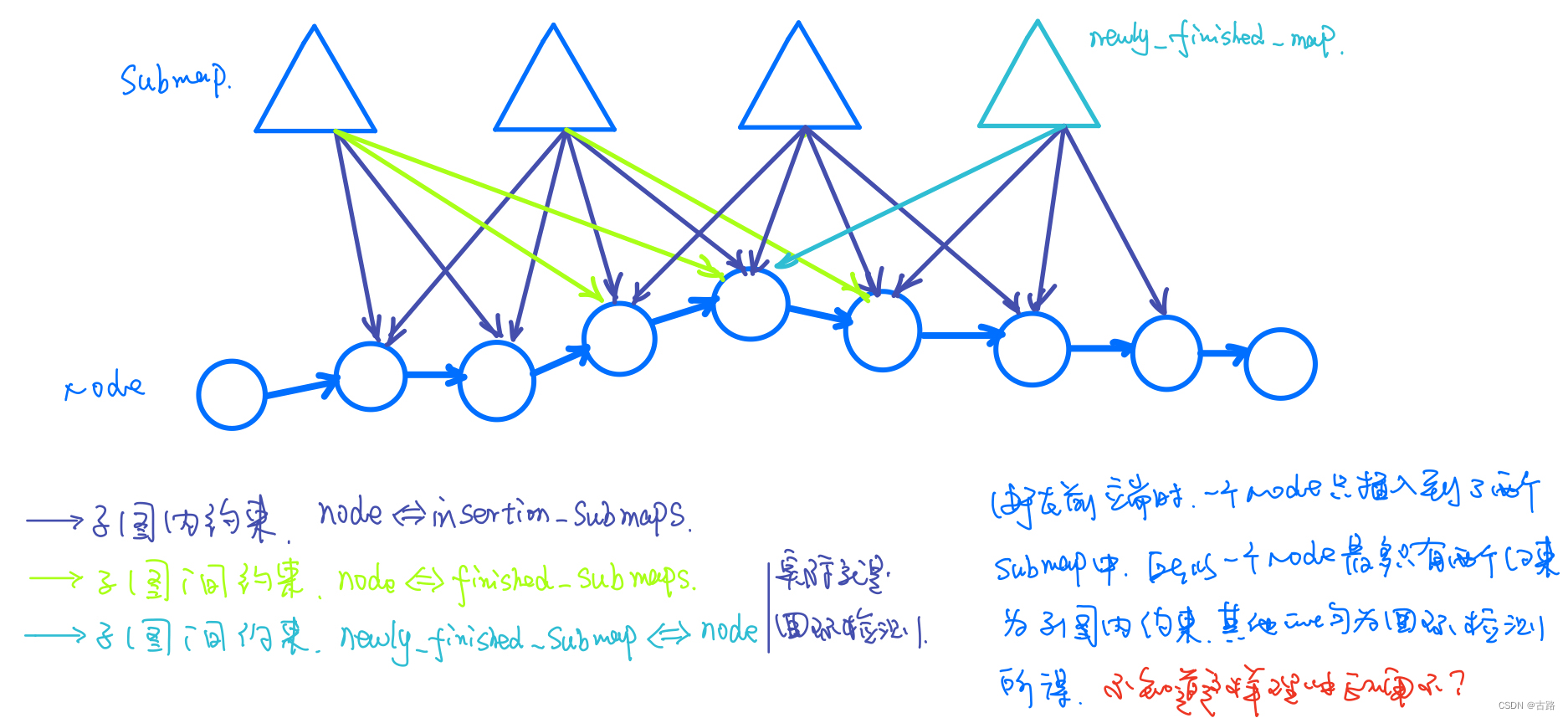
1.设置待优化变量

• 子图的global_pose
• 节点的global_pose_2d

2.残差项

2.1.第一种残差-scan_match

将节点与子图原点在global坐标系下的相对位姿 与 约束 的差值作为残差项

• 第一种坐标变换: 节点与子图原点在global坐标系下的坐标变换（预测位姿）
• 第二种坐标变换: 子图内约束与子图间约束（测量位姿）

残差计算代码：

/**
 * @brief 2d 根据SPA论文里的公式求残差
 * 
 * 计算残差：
 * T12 = T1.inverse() * T2
 * [R1.inverse * R2,  R1.inverse * (t2 -t1)]
 * [0              ,  1                    ]
 * 
 * @param[in] relative_pose 
 * @param[in] start 
 * @param[in] end 
 * @return std::array<T, 3> 
 */
template <typename T>
static std::array<T, 3> ComputeUnscaledError(
    const transform::Rigid2d& relative_pose, const T* const start,
    const T* const end) {
  // 旋转矩阵R
  const T cos_theta_i = cos(start[2]);
  const T sin_theta_i = sin(start[2]);
  const T delta_x = end[0] - start[0]; // t2 -t1
  const T delta_y = end[1] - start[1];
  const T h[3] = {cos_theta_i * delta_x + sin_theta_i * delta_y, // R.inverse * (t2 -t1)
                  -sin_theta_i * delta_x + cos_theta_i * delta_y,
                  end[2] - start[2]};
  return {{T(relative_pose.translation().x()) - h[0],
           T(relative_pose.translation().y()) - h[1],
           common::NormalizeAngleDifference(
               T(relative_pose.rotation().angle()) - h[2])}};
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

2.2.第二种残差-Landmark

landmark数据 与 通过2个节点位姿插值出来的相对位姿 的差值作为残差项

• 第一种坐标变换: landmark数据的时间在2个节点位姿中插值出来的位姿（预测位姿）
• 第二种坐标变换: landmark数据中的landmark_to_tracking_transform_（测量位姿）

  struct LandmarkNode {
    // landmark数据是相对于tracking_frame的相对坐标变换
    struct LandmarkObservation {
      int trajectory_id;
      common::Time time;
      transform::Rigid3d landmark_to_tracking_transform;
      double translation_weight;
      double rotation_weight;
    };
    // 同一时刻可能会观测到多个landmark数据
    std::vector<LandmarkObservation> landmark_observations;
    // 这帧数据对应的tracking_frame在global坐标系下的位姿
    absl::optional<transform::Rigid3d> global_landmark_pose;
    bool frozen = false;
  };
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

主要是node <--> landmark 之间的约束：

  // Step: landmark数据 与 通过2个节点位姿插值出来的相对位姿 的差值作为残差项
  AddLandmarkCostFunctions(landmark_nodes, node_data_, &C_nodes, &C_landmarks,
                           &problem, options_.huber_scale());
1
2
3

略.

2.3.第三种残差-Odometer

节点与节点间在global坐标系下的相对坐标变换 与 通过里程计数据插值出的相对坐标变换 的差值作为残差项

• 第一种坐标变换: 相邻2个节点间在global坐标系下的坐标变换
• 第二种坐标变换: 再分别计算这2个节点的时间在里程计数据队列中插值得到的2个里程计位姿, 计算这2个里程计位姿间的坐标变换

2.4.第四种残差-local_global

节点与节点间在global坐标系下的相对坐标变换 与 相邻2个节点在local坐标系下的相对坐标变换 的差值作为残差项

• 第一种坐标变换: 相邻2个节间在global坐标系下的坐标变换
• 第二种坐标变换: 相邻2个节点在local坐标系下的坐标变换

2.5.第五种残差-gps

节点与gps坐标系原点在global坐标系下的相对坐标变换 与 通过gps数据进行插值得到的相对坐标变换 的差值作为残差项

• 第一种坐标变换: 节点对应的时刻在gps数据中插值得到的gps相对于gps坐标系原点的位姿
• 第二种坐标变换: 节点在global坐标系下 与 gps坐标系原点 的相对坐标变换

3.理论参考

• 参考1
• 参考2