OpenCV笔记整理【傅里叶变换】

傅里叶变换的作用：

可以实现图像增强、图像去噪、边缘检测、特征提取、图像压缩、图像加密。

常用的图像处理方式有两种，傅里叶变换属于频率域处理。

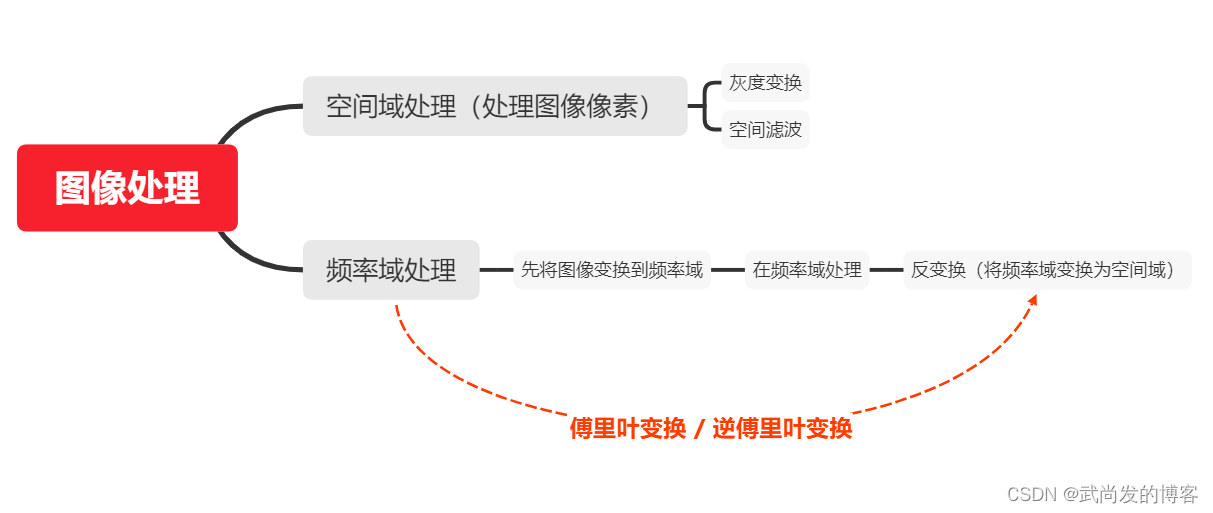
1. 理论基础：

下面是某饮料的放入时间、放入数量的配方表

• 每隔1分钟放1块冰糖
• 每隔2分钟放3粒红豆
• 每隔3分钟放2粒绿豆
• 每隔4分钟放4个西红柿
• 每隔5分钟放1杯纯净水

时域分析：

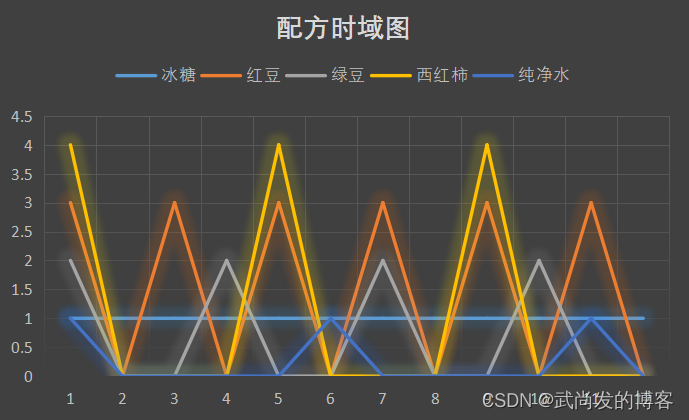
任何周期函数都可以表示为不同频率的正弦函数形式，比如：
y=3sin(0.8x)+7sin(0.5x)+2sin(0.2x) 函数对应的函数曲线：

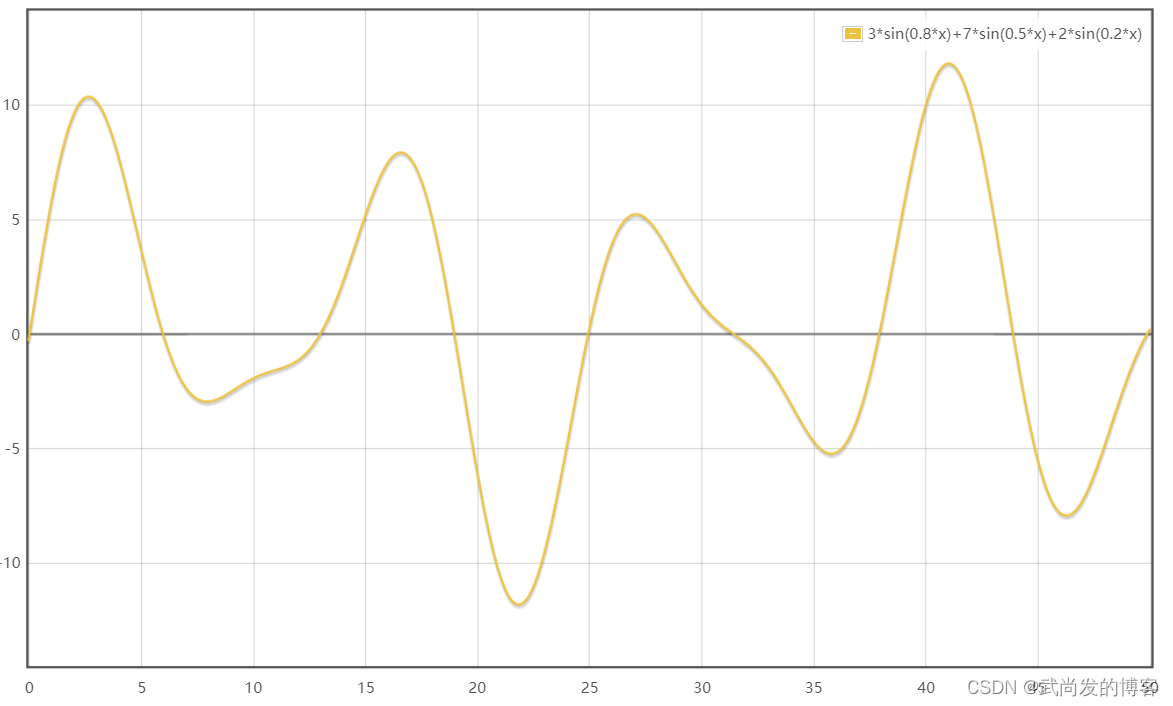
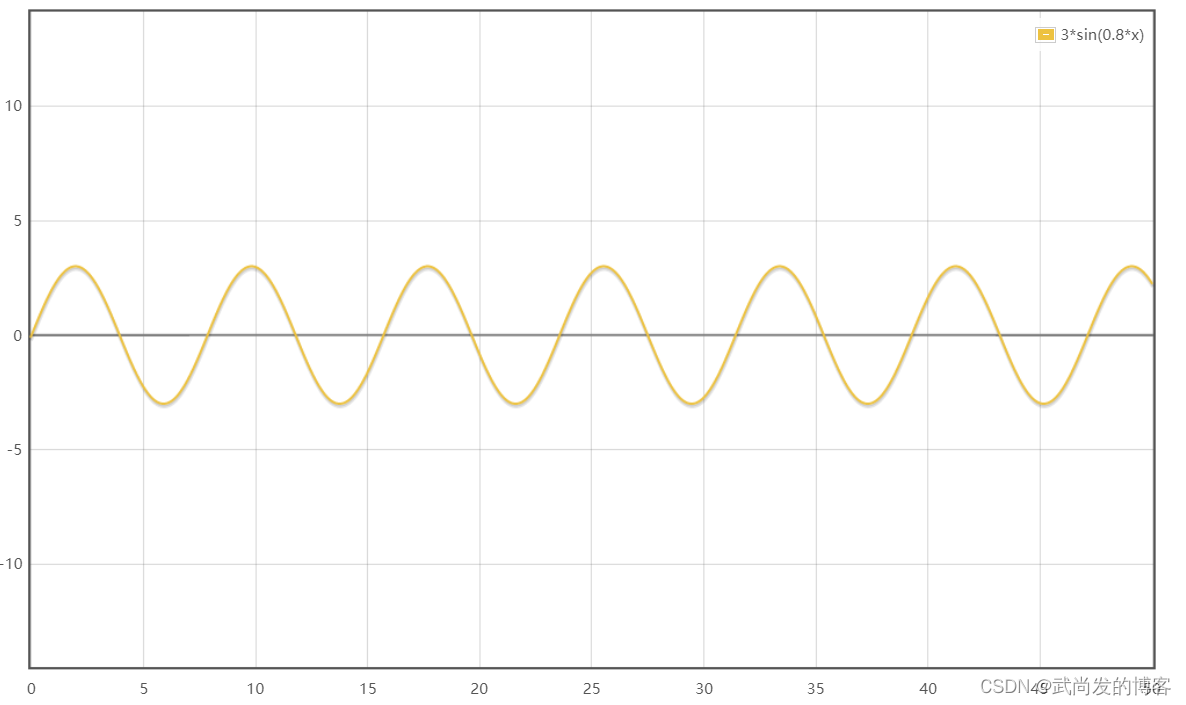
该函数由下面三个函数的和构成：

• 3sin(0.8x)
  

• 7sin(0.5x)
  

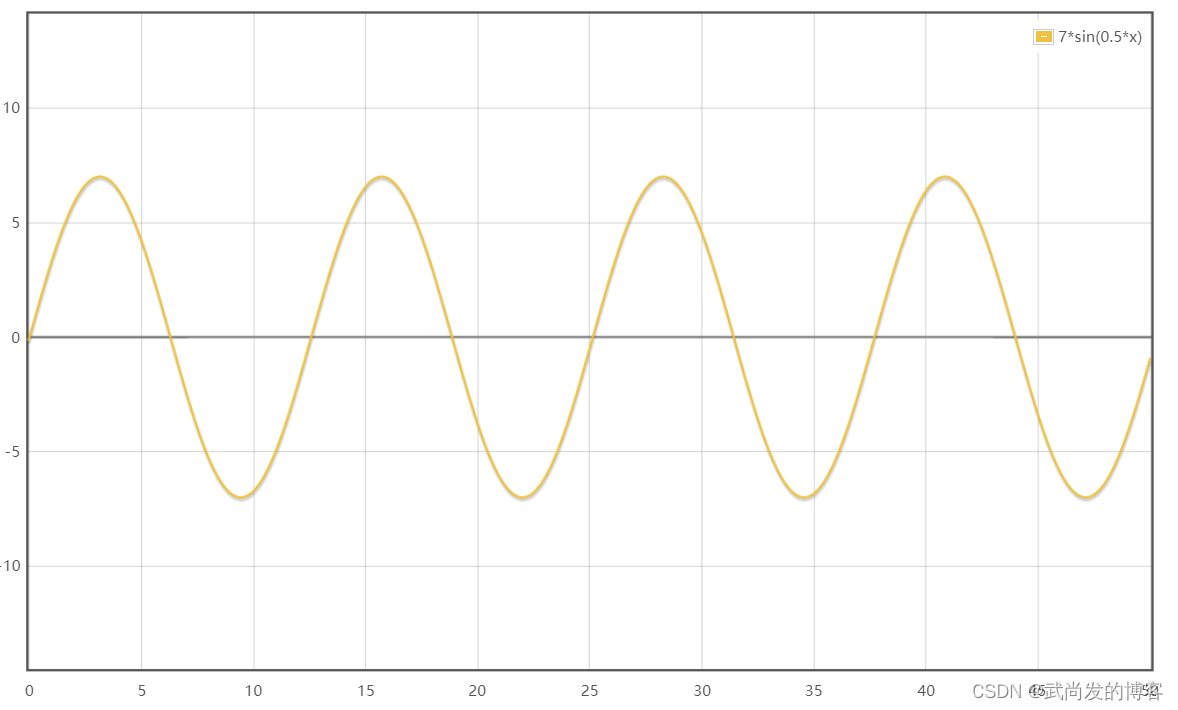
• 2sin(0.2x)
  

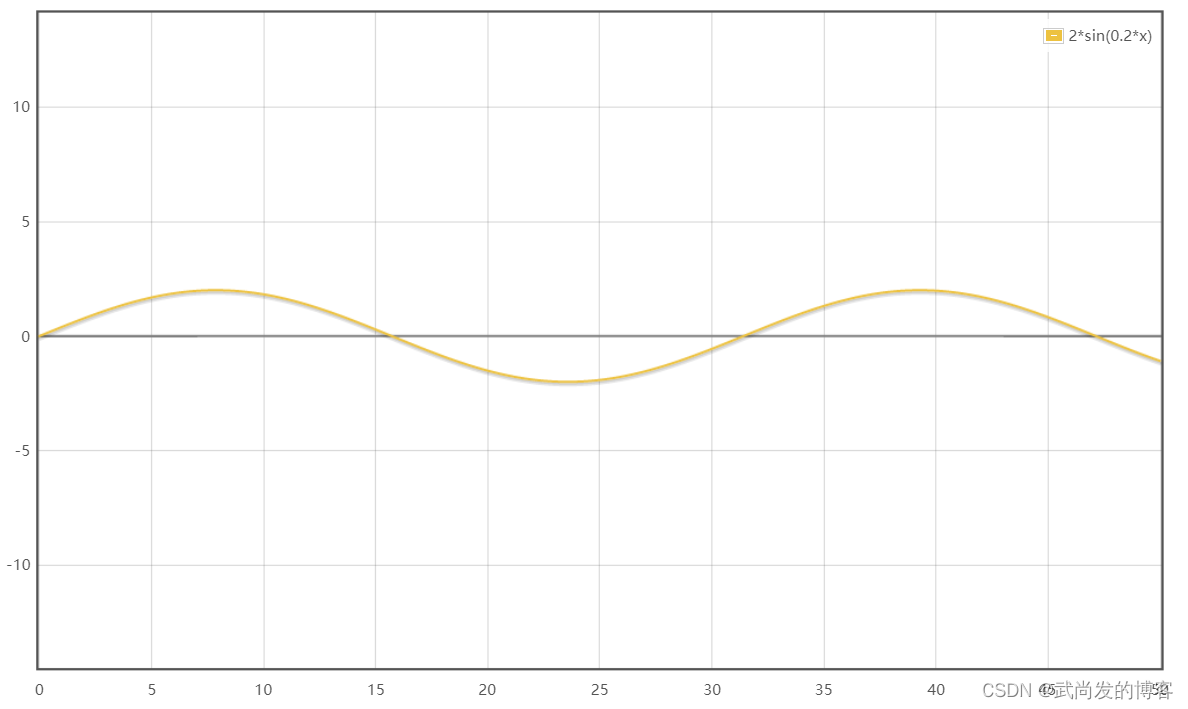
前面的三个正弦函数分别表示下图中的三个柱子：

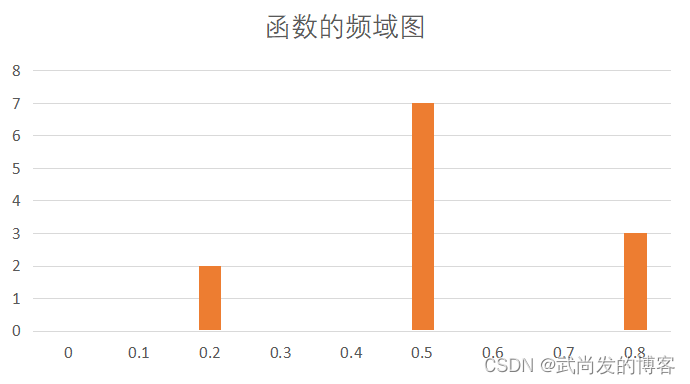
相差：
前面的函数都是从 “00：00” 开始的，但是如果时间从“00：02” 分开始，这个时间差就是相差。

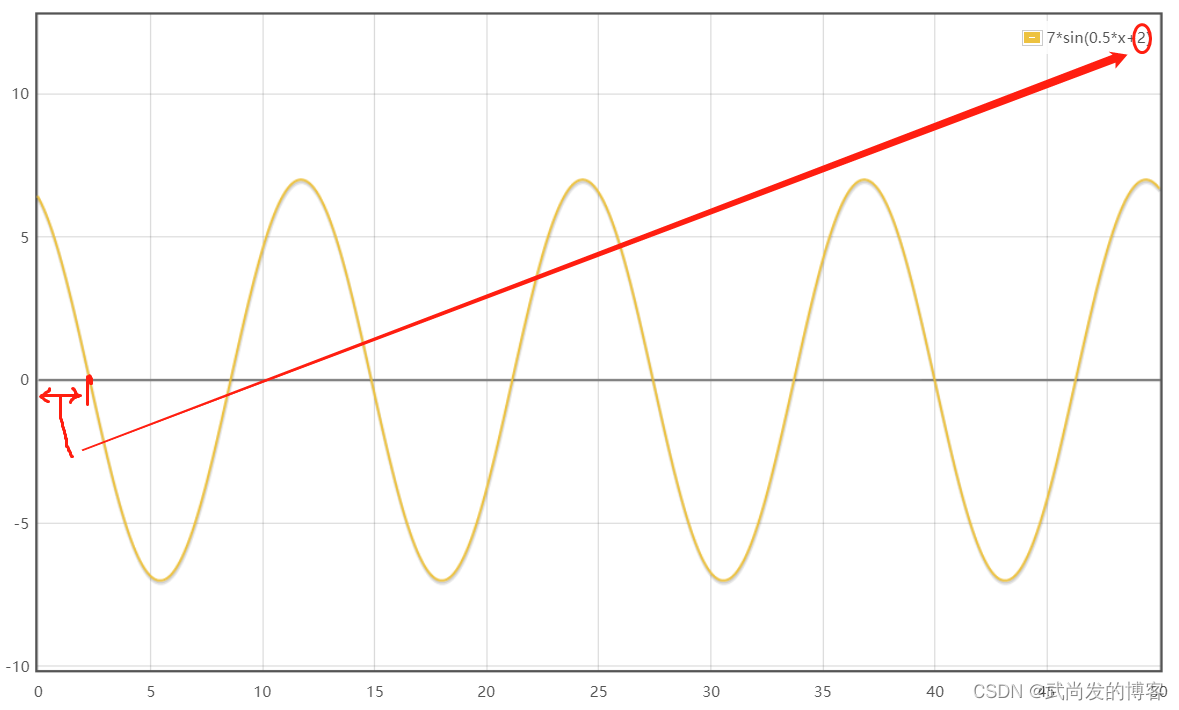
低频： 图像内变化缓慢的灰度分量，例如草原上的青草。
高频： 图像中变化越来越快的灰度分量，例如草原上的狮子轮廓。

2. Numpy实现傅里叶变换：

返回值 = numpy.fft.fft2(原始频谱)

• 原始图像：类型为灰度图像。
• 返回值：返回一个数组。

上代码：

import cv2
import numpy as np
import matplotlib.pyplot as plt


img = cv2.imread('image\\lena.bmp',0)

# 傅里叶变换
f = np.fft.fft2(img) 

# 将频率为0的分量从默认的左上角移至图像中心
fshift = np.fft.fftshift(f)  

# 将数组分度到【0-255】灰度空间内，方便显示
magnitude_spectrum = 20*np.log(np.abs(fshift)) 

plt.subplot(121)
plt.imshow(img, cmap = 'gray')
plt.title('originalImg')
plt.axis('off')

plt.subplot(122)
plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('fftImg')
plt.axis('off')

plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

运行：

3. 逆傅里叶变换：

返回值 = numpy.fft.ifft2(原始频谱)

上代码：

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('image\\boat.bmp',0)

# 傅里叶变换
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)

# 将0频率分量恢复至左上角
ishift = np.fft.ifftshift(fshift)

# 逆傅里叶变换 
iimg = np.fft.ifft2(ishift)

# 将逆傅里叶的结果数组分度到【0-255】灰度空间
iimg = np.abs(iimg)

plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('originalImg'),plt.axis('off')

plt.subplot(122),plt.imshow(iimg, cmap = 'gray')
plt.title('ifftImg'),plt.axis('off')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

运行：

3. 高频滤波：

滤波器允许一定频率的分量通过，或者拒绝通过。
作用：可以实现图像增强、图像去噪、边缘检测、特征提取、压缩、加密。

• 高频滤波器：允许高频信号通过。
• 低频滤波器：允许低频信号通过。

上代码：

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('image\\lena.bmp',0)

f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)

# 获取原图像的分辨率
rows, cols = img.shape 
 # 计算中心点
crow,ccol = int(rows/2) , int(cols/2)

# 在傅里叶变换的频谱图像上建立一块矩形[x从中心开始正负30，y从中心开始正负30]
# 该区域覆盖了低频分量，保留了高频
# 将该低频分量的灰度赋值为0（抛弃）
fshift[crow-60:crow+60, ccol-60:ccol+60] = 0
fftImg=20*np.log(np.abs(fshift))

# 逆傅里叶变换
ishift = np.fft.ifftshift(fshift)
iimg = np.fft.ifft2(ishift)
iimg = np.abs(iimg)

plt.subplot(131),plt.imshow(img, cmap = 'gray')
plt.title('originalImg'),plt.axis('off')

plt.subplot(132),plt.imshow(fftImg, cmap = 'gray')
plt.title('fftImg'),plt.axis('off')

plt.subplot(133),plt.imshow(iimg, cmap = 'gray')
plt.title('resultImg'),plt.axis('off')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

运行：

4. OpenCV中实现傅里叶变换：

• 傅里叶变换返回结果 = cv2.dft (原始图像，转换标识)

原始图像：需要使用np.float32()函数转换格式。
转换标识：通常为 “cv2.DFT_COMPLEX_OUTPUT”。
返回结果：与numpy不同，这里返回的是一个双通道的值 [通道一为实部、通道二为虚部] 。

cv2.magnitude(实部，虚部) 作用：计算频谱信息的幅度。

上代码：

import numpy as np
import cv2
import matplotlib.pyplot as plt

img = cv2.imread('image\\lena.bmp',0)

# 傅里叶变换
dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)

# 将0频率分量移至中心，得到新频谱
dftShift = np.fft.fftshift(dft)

# 计算频谱信息的幅度
# 将幅度值分度到灰度空间[0-255]
result = 20*np.log(cv2.magnitude(dftShift[:,:,0],dftShift[:,:,1]))


plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('original'),plt.axis('off')

plt.subplot(122),plt.imshow(result, cmap = 'gray')
plt.title('result'), plt.axis('off')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

5. OpenCV中实现逆傅里叶变换：

• 逆傅里叶变换返回结果 = cv2.idft (原始图像，转换标识)

上代码：

import numpy as np
import cv2
import matplotlib.pyplot as plt

img = cv2.imread('image\\lena.bmp',0)

# 傅里叶变换
dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)

# 将o频率分量移至中心
dftShift = np.fft.fftshift(dft)

# 将o频率分量复位至左上角
ishift = np.fft.ifftshift(dftShift)

# 逆傅里叶变换
iImg = cv2.idft(ishift)

# 计算频谱信息的幅度
iImg= cv2.magnitude(iImg[:,:,0],iImg[:,:,1])

plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('originalImg'), plt.axis('off')

plt.subplot(122),plt.imshow(iImg, cmap = 'gray')
plt.title('inverseImg'), plt.axis('off')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

运行：

6. 低通滤波：

上代码：

import numpy as np
import cv2
import matplotlib.pyplot as plt


img = cv2.imread('image\\lena.bmp',0)

# 傅里叶变换
dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
dftShift = np.fft.fftshift(dft)
dftShiftImg = 20*np.log(cv2.magnitude(dftShift[:,:,0],dftShift[:,:,1]))

# 绘制掩模区域
rows, cols = img.shape
crow,ccol = int(rows/2) , int(cols/2)
mask = np.zeros((rows,cols,2),np.uint8) #两个通道，与频谱图像匹配
mask[crow-20:crow+20, ccol-20:ccol+20] = 1
fShift = dftShift*mask # 保留中间的低频分量
fShiftImg = 20*np.log(cv2.magnitude(fShift[:,:,0],fShift[:,:,1]))

# 逆傅里叶变换
ishift = np.fft.ifftshift(fShift)
iImg = cv2.idft(ishift)
iImg= cv2.magnitude(iImg[:,:,0],iImg[:,:,1])


plt.subplot(222),plt.imshow(img, cmap = 'gray')
plt.title('original'), plt.axis('off')

plt.subplot(221),plt.imshow(dftShiftImg, cmap = 'gray')
plt.title('dftShiftImg'), plt.axis('off')

plt.subplot(223),plt.imshow(fShiftImg, cmap = 'gray')
plt.title('fShiftImg'), plt.axis('off')

plt.subplot(224),plt.imshow(iImg, cmap = 'gray')
plt.title('result'), plt.axis('off')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

运行：

如有错误，欢迎批评指正，路过点个关注，谢谢。。。