【9. 子矩阵和】

子矩阵和（二维前缀和）

思路：

计算子矩阵的和，例如以（x1,y1）为左上角，（x2,y2）为右上角的子矩阵的和为多少。

需要解决俩个问题

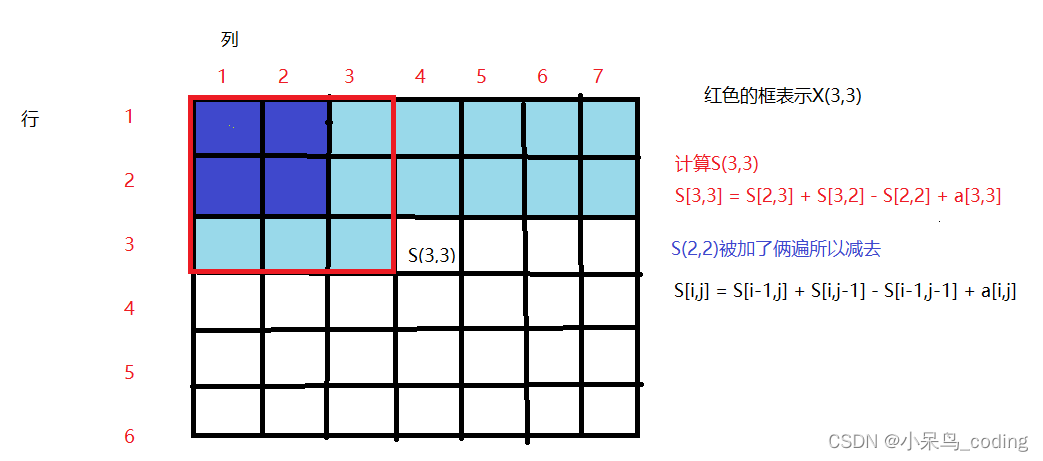
1. s [ i , j ]如何计算
   一行一行的计算

S[i,j] = S[i-1,j] + S[i,j-1] - S[i-1,j-1] + a[i,j]
1

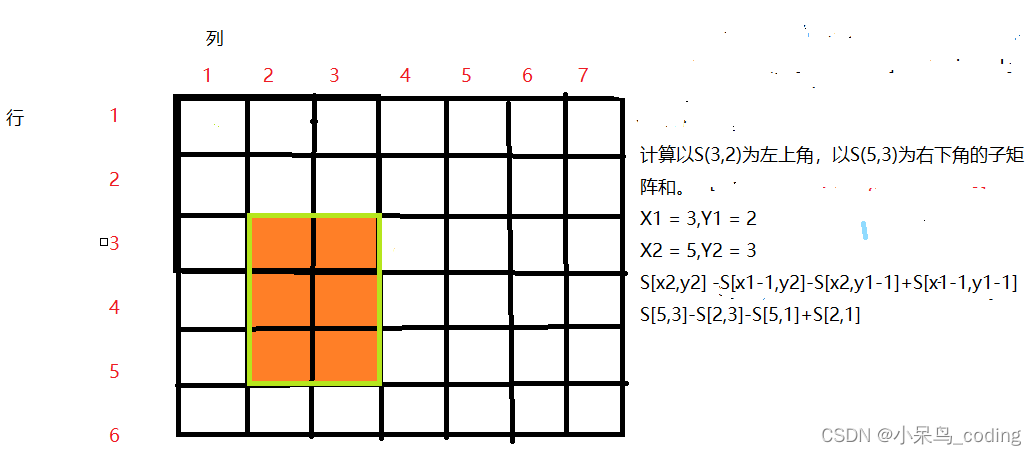
2. 以(x1,y1)为左上角,(x2,y2)为右下角这一子矩阵中所有数的和该如何计算

S[x2,y2] -S[x1-1,y2]-S[s2,y1-1]+S[x1-1,y1-1]
1

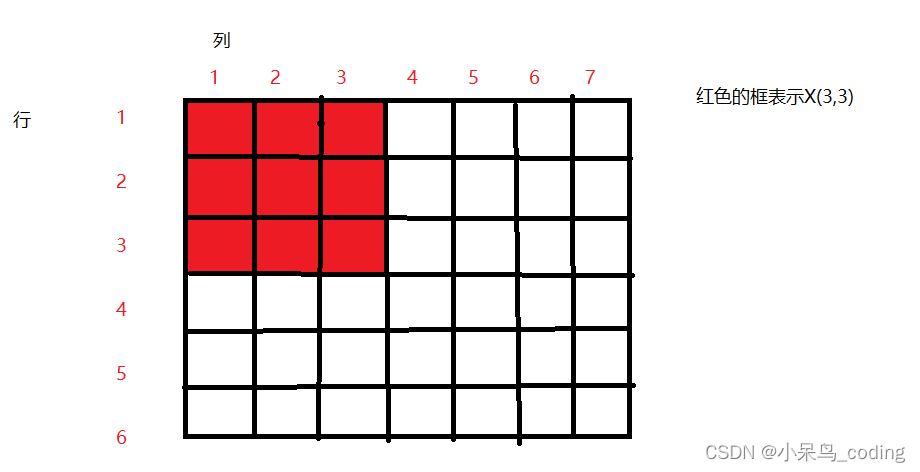
题目

输入一个 n 行 mm 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1,y1,x2,y2表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式

第一行包含三个整数 n，m，q

接下来 n 行，每行包含 m个整数，表示整数矩阵。

接下来 q行，每行包含四个整数 x1,y1,x2,y2表示一组询问。

输出格式

共 q 行，每行输出一个询问的结果。

数据范围

1 ≤ n ,m ≤ 1000
1 ≤ q ≤ 200000
1≤ x1 ≤ x2 ≤ n
1 ≤ y1 ≤ y2 ≤ m
−1000 ≤ 矩阵内元素的值 ≤ 1000

输入样例：

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
1
2
3
4
5
6
7

输出样例：

17
27
21


1
2
3
4
5

代码

#include <iostream>
using namespace std;
const int N = 1010;

int n, m, q;
int a[N][N],s[N][N];

int main()
{
   scanf("%d%d%d",&n ,&m, &q);
   for (int i = 1; i <= n; i ++)    //给数组赋值
       for (int j = 1; j <= m; j ++)
           scanf("%d",&a[i][j]);        
           
   //初始化前缀和数组
   for (int i = 1; i <= n; i ++)
       for (int j = 1; j <= m; j ++)
           s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
           
   //输出前缀和
   while (q --)
   {
       int x1,y1,x2,y2;
       scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
       printf("%d\n",s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1]);
   }
   return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28