1 题目简介

题目来源于2019年中国研究生数学建模竞赛D题——汽车行驶工况构建。

2 涉及内容

在本次实战的数据分析过程中，涉及以下技术内容：
（1）数据预处理技术
（2）for循环的使用
（3）暴力搜索方法

3 实战步骤

3.1 读取数据

我将三个数据表合成了一个，

dir_data='2019年中国研究生数学建模竞赛D题\原始数据\汇总.xlsx';
warning('off');
data_raw=readtable(dir_data);

%取出时间和速度
time=data_raw{:,1};
time_num=datenum(time);%将时间类型转换为double类型
chesu=data_raw{:,2};
1
2
3
4
5
6
7
8

3.2 速度线性插值

如果两点间隔小于5秒，对两点之间的速度进行线性插值，按1秒的间隔补足速度点，

time_second=time_num(2)-time_num(1);%一秒的大小
x_cha=[];%存放要插值的时间点

for i=2:length(time_num)
    time_jiange=time_num(i)-time_num(i-1);
    if (time_jiange>time_second) && (time_jiange<=5*time_second)     
        tem1=time_num(i-1):time_second:time_num(i);
        x_cha=[x_cha,tem1];
    end
end
chesu_cha=interp1(time_num,chesu,x_cha,"linear");%线性插值

%按时间升序重新排序，实现把新插值点和原数据点合在一起
chesu_zeng=[chesu;chesu_cha'];
time_num_zeng=[time_num;x_cha'];

[time_num_zeng,I] = sort(time_num_zeng);
chesu_zeng=chesu_zeng(I);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

3.3 标记断点位置

两点时间间隔超过5秒的，视为断点，对其位置进行标记，

duan=zeros(length(time_num_zeng),1);%标记断点位置，1表示是断点
for i=2:length(time_num_zeng)
    time_jiange=time_num_zeng(i)-time_num_zeng(i-1);
    if time_jiange>5*time_second
        duan(i)=1; 
    end 
end
1
2
3
4
5
6
7

3.4 丢弃小于20秒的片段

两个断点之间的片段如果小于20秒，则丢弃，

duan_ind=find(duan==1);
del_ind=[];%存放要删除的点的索引位置
if (time_num_zeng(duan_ind(1)-1)- time_num_zeng(1))<20*time_second %判断第一个断点之前的部分是否少于20秒
    tem1=1:(duan_ind(1)-1);
    del_ind=[del_ind,tem1];
end

for i=2:length(duan_ind) %判断第二个断点到最后一个断点之间的部分是否少于20秒
    if (time_num_zeng(duan_ind(i)-1)- time_num_zeng(duan_ind(i-1)))<20*time_second
        tem1=duan_ind(i-1):(duan_ind(i)-1);
        del_ind=[del_ind,tem1];
    end 
end

if (time_num_zeng(end)- time_num_zeng(duan_ind(end)))<20*time_second %判断最后一个断点之后的部分是否少于20秒
    tem1=duan_ind(end):length(time_num_zeng);
    del_ind=[del_ind,tem1];
end

time_num_zeng(del_ind)=[];
chesu_zeng(del_ind)=[];%执行删除操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

3.5 重新锁定断点位置

执行上述删除操作后，断点位置发生变化，需重新锁定断点位置，

duan=zeros(length(time_num_zeng),1);
for i=2:length(time_num_zeng)
    time_jiange=time_num_zeng(i)-time_num_zeng(i-1);
    if time_jiange>5*time_second
        duan(i)=1; 
    end 
end
1
2
3
4
5
6
7

3.6 形成分时片段

车速按断点分段，存于fen_chesu中，形成"分时片段"，

f_duan=find(duan==1);
fen_chesu={};
for i=2:length(f_duan)
    fen_chesu{i}=chesu_zeng(f_duan(i-1):f_duan(i)-1);     
end
fen_chesu{1}=chesu_zeng(1:f_duan(1)-1);%第一个断点前和最后一个断点后做特殊处理
fen_chesu{i+1}=chesu_zeng(f_duan(i):end);
1
2
3
4
5
6
7

3.7 缩短怠速时间

针对每段分时片段，因为长时间低速行驶（包括停车）可能意味异常状况，如突发情况造成的严重堵车、停车等人等，所以这里我将低速时间段（小于10km/h）大于200s的缩短成200s，

for i=1:length(fen_chesu)
    tem1=fen_chesu{i}; %取出每段车速
    ind1=find(tem1<10); %找到车速低于10km/h的点的位置索引
    del_200=[]; %存放需删除的索引
    if ~isempty(ind1) %能找到车速低于10km/h的点
        tem2=ind1(1); %车速低于10km/h的时间段左端点索引
        %下边for循环寻找车速连续低于10km/h的片段
        for j=2:length(ind1) %一个数一个数挨着找
            if (ind1(j)-ind1(j-1))~=1 %如果当前位置索引与上一位置索引之差不是1
                if (ind1(j-1)-tem2+1)>200 %如果上一位置索引与左端点索引之差大于200s
                    del_200=[del_200,(tem2+200):ind1(j-1)]; %将200s以后的的索引加到del_200中
                    tem2=ind1(j); %更新左端点索引，继续寻找   
                end
            end
        end
        if (ind1(j)-tem2+1)>200 %此处对最后一段车速连续低于10km/h的点进行处理     
            del_200=[del_200,(tem2+200):ind1(j)];
        end
       
    end
    tem1(del_200)=[];%删除大于200s的索引对应的数据
    fen_chesu{i}=tem1;%重新存回去

end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

3.8 查看异常加速度分布

%查看异常加速度点的分布情况
all_a=[];
for i=1:length(fen_chesu)
    tem1=fen_chesu{i};
    for j=2:length(tem1)
        all_a=[all_a;(tem1(j)-tem1(j-1))/3.6]; 
    end
end
figure,histogram(all_a);
figure,plot(all_a,'bo');
1
2
3
4
5
6
7
8
9
10

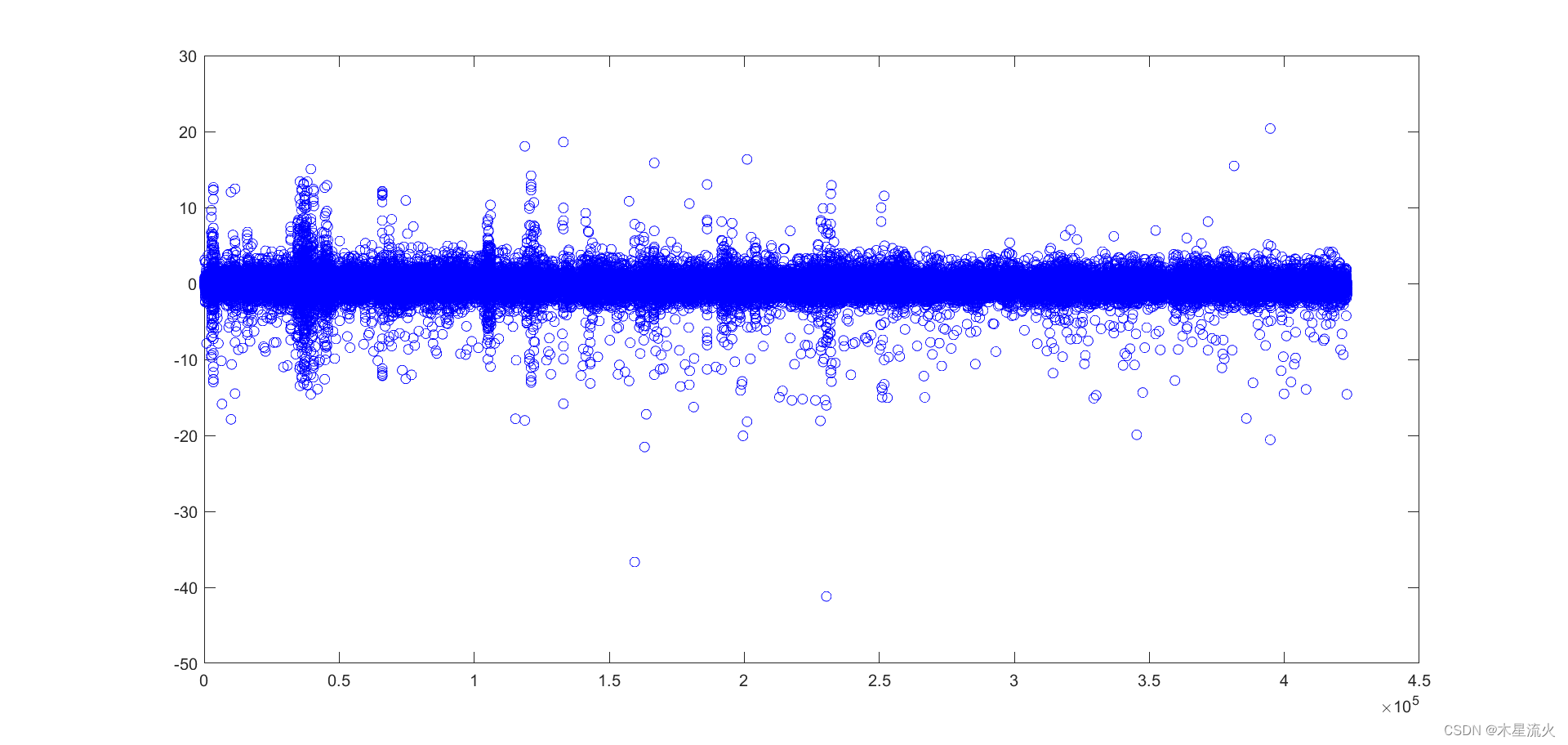
3.9 处理加速度异常点

从上图可以看出，有些加速度过大，超过了车辆本身所能达到的加速度，应当视为异常点，下面针对每个分时片段的车速，对加速度超过3.97和减速度大于7.5的速度点进行插值，

k=1;
for i=1:length(fen_chesu)
    tem1=fen_chesu{i};
    cha_ind=[];
    for j=2:length(tem1)
        jiasudu=(tem1(j)-tem1(j-1))/3.6;%注意转化为m/s
        if (jiasudu>3.97) || (jiasudu<-7.5)
            cha_ind=[cha_ind,j];
        end 
    end
    Lia = ismember(2,cha_ind);
    if Lia
        cha_ind=[1,cha_ind]; %假设第一个点的加速度和第二个点的相同
    end
    if ~isempty(cha_ind)
        C = setdiff(1:length(tem1),cha_ind); %用非异常点对异常点进行插值
        cha_y=interp1(C,tem1(C),cha_ind,"linear");%线性插值
        if k<4 %画3个插值前后对比曲线
            tem2=tem1;
            tem2(cha_ind)=cha_y;
            figure,plot(1:length(tem1),tem1,'r-',1:length(tem1),tem2,'b-');
            k=k+1;
        end
        tem1(cha_ind)=cha_y;
        fen_chesu{i}=tem1; %使用插值后的加速度正常的车速点更新车速
    end
    
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

画出前三个需插值的分时片段，直观对比插值前后速度点的变化，红色线为插值前的速度点，蓝色线为插值后的速度点，可见插值后加速度异常点变得平顺。

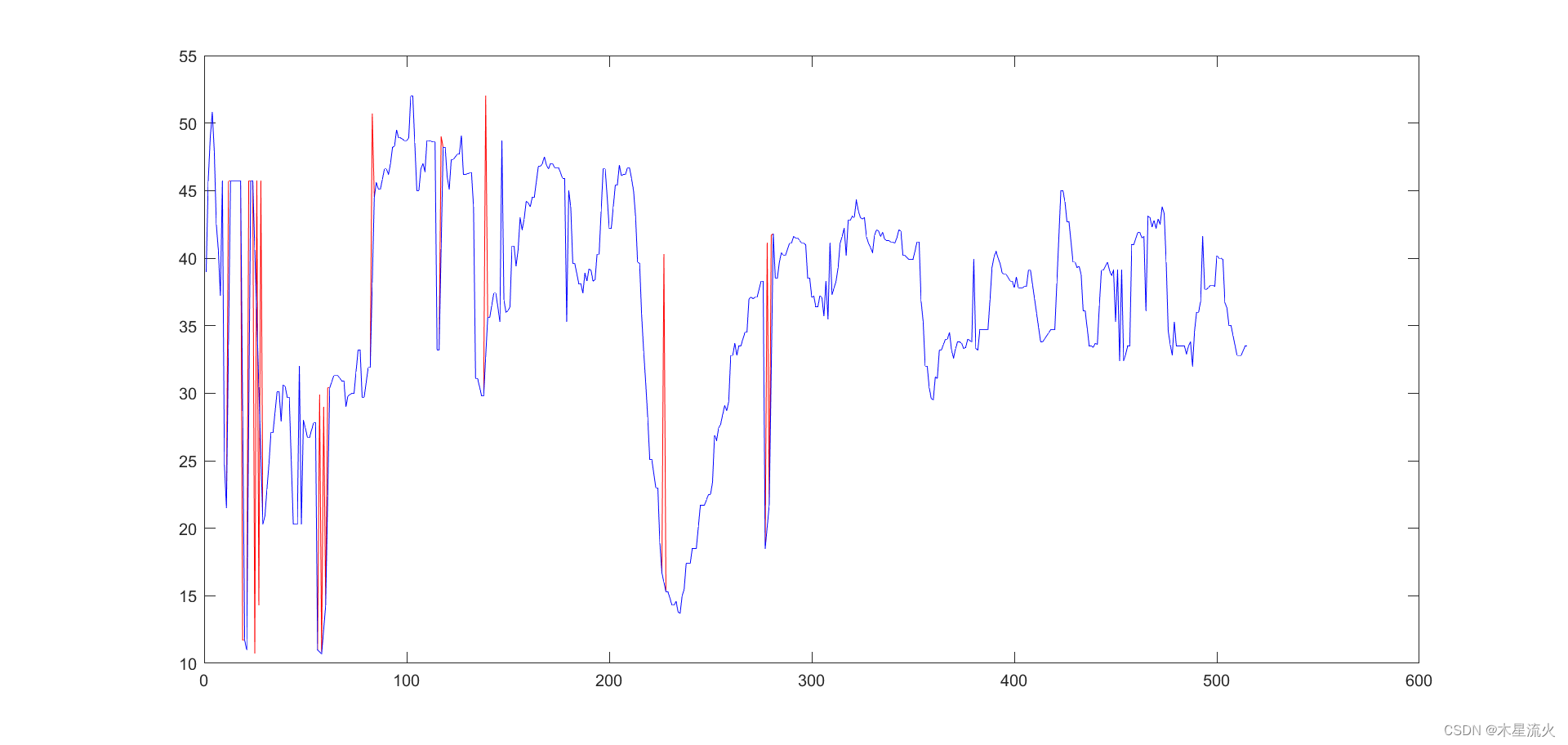
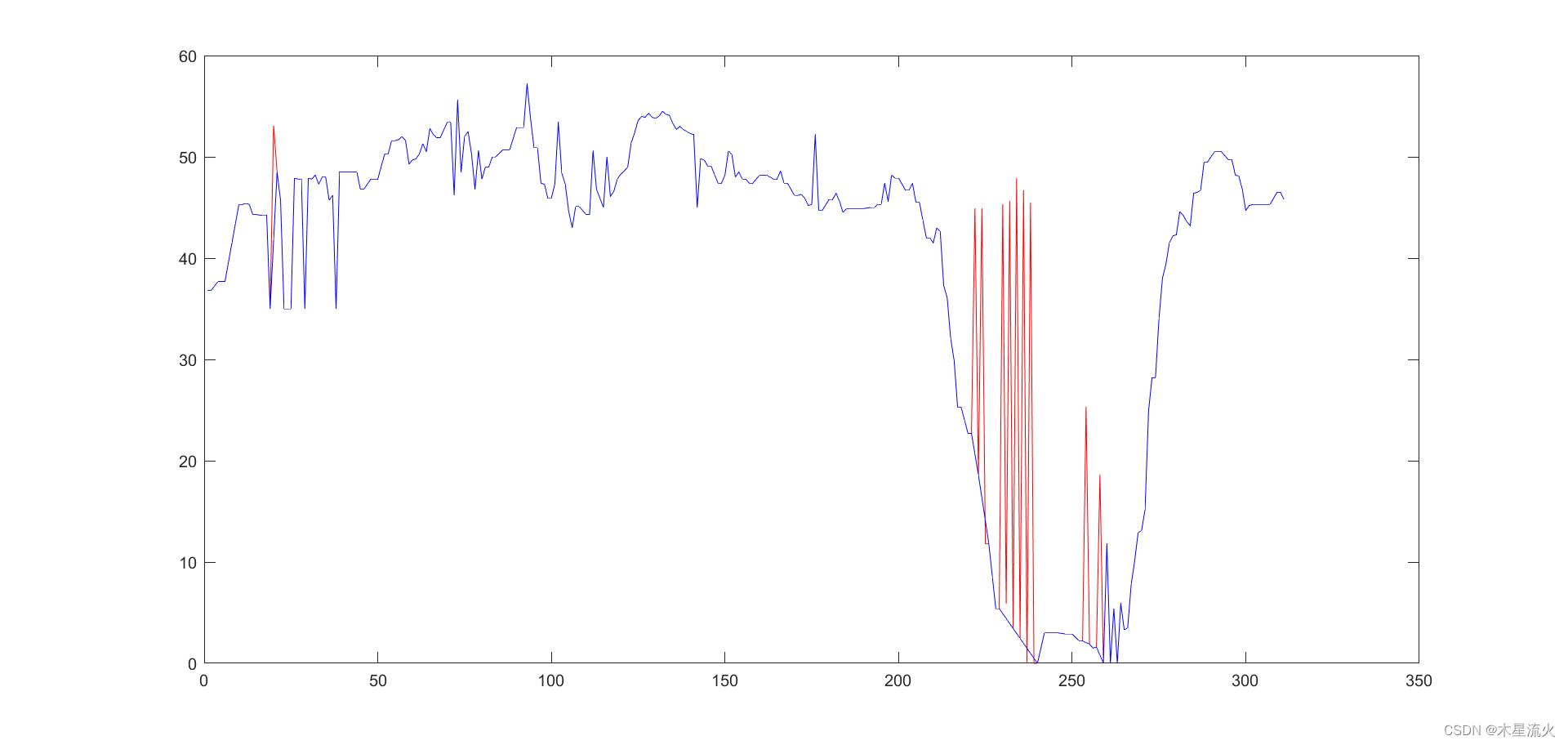
3.10 运动学片段的生成

我们规定一个运动学片段为一段怠速片段（小于10km/h）和与其相连的一段正常行驶片段（大于10km/h）组合而成，

%按怠速+正常行驶对速度进行分段，生成各运动学片段
yundong={};
k=1;
for i=1:length(fen_chesu)
    tem1=fen_chesu{i};
    ind1=~(tem1<10); %车速小于10的视为0，大于10的视为1
    ind2=ind1;
    ind1(end)=[];
    ind2(1)=[];
    cha=ind2-ind1; %求各速度点两两之间的差值
    tem2=find(ind1==0);
    if ~isempty(tem2)
        tou=tem2(1); %将第一个车速小于10的点的索引赋值为左端点的初始值
        for j=(tou+1):length(cha) %从左端点向右寻找
            if cha(j)==-1 %发现下降沿
                yundong{k}=tem1(tou:j); %从左端点到下降沿即为一个运动学片段
                k=k+1;
                tou=j+1; %更新左端点
            end
        end
        
        %每个分时片段的最后一段运动学片段可能没有下降沿，所以做特殊处理
        find_1=find(cha==1);
        if (~isempty(find_1))&&(find_1(end)>tou)
            yundong{k}=tem1(tou:end);
            k=k+1;
        end
    end
    
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

删除长度小于20秒的运动学片段，

del_cell=[];
 for i=1:length(yundong)
    if length(yundong{i})<20
       del_cell=[del_cell,i]; 
    end 
 end
 yundong(del_cell)=[];
1
2
3
4
5
6
7

观察各运动学片段长度的分布情况，

len_cell=[];
 for i=1:length(yundong)
       len_cell=[len_cell;length(yundong{i})];  
 end
 histogram(len_cell);
1
2
3
4
5

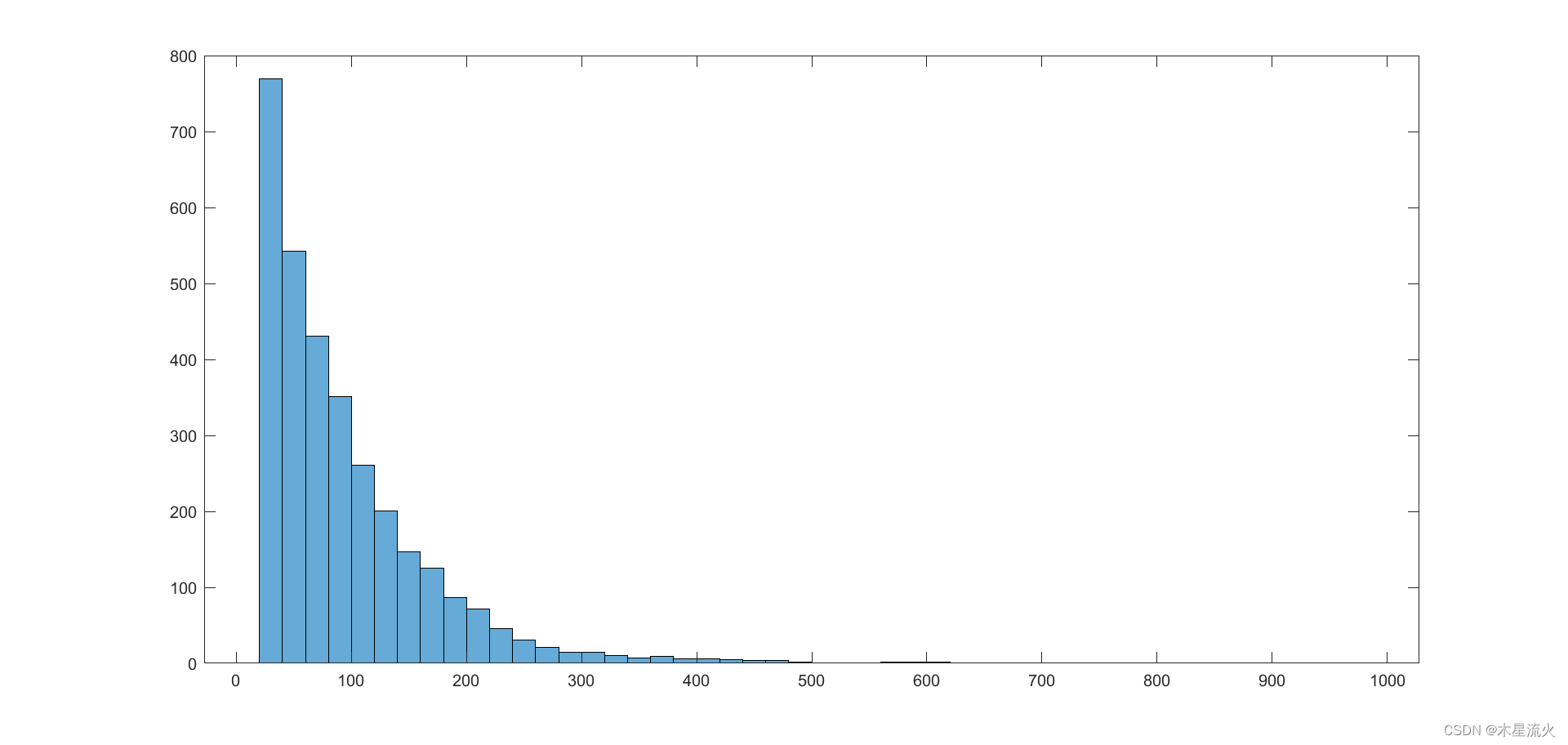
随机画一个运动学片段，观察形状，

3.11 计算各运动学片段的特征参数

总共需计算平均速度、平均行驶速度（非怠速）、平均加速度、平均减速度、速度标准差、加速度标准差、减速度标准差、怠速时间占比、匀速时间占比、加速时间占比、减速时间占比等11个特征参数的值，保存在矩阵tezheng中，一行是一个运动学片段（即一个样本），一列代表一个特征参数。

%计算各个运动学片段的特征参数
tezheng=[];
all_chesu=[];
all_jiasudu=[];
for i=1:length(yundong)
    tem1=yundong{i};
    %平均速度
    var1=mean(tem1);
    %平均行驶速度
    var2=mean(tem1(tem1>10));
    %平均加速度
    a_all=diff(tem1);
    a_all=[a_all(1);a_all];
    var3=mean(a_all(a_all>0))/3.6;
    %平均减速度
    var4=mean(a_all(a_all<0))/3.6;
    %速度标准差
    var5=std(tem1);
    %加速度标准差
    var6=std(a_all(a_all>0));
    %减速度标准差
    var7=std(a_all(a_all<0));
    %怠速时间占比
    var8=sum(tem1<10)/length(tem1);
    %匀速时间占比
    var9=sum(a_all==0)/length(a_all);
    %加速时间占比
    var10=sum(a_all>0)/length(a_all);
    %减速时间占比
    var11=sum(a_all<0)/length(a_all);
    tem2=[var1 var2 var3 var4 var5 var6 var7 var8 var9 var10 var11];
    tezheng=[tezheng;tem2];
    
    
    all_chesu=[all_chesu;tem1]; %存储整个运动学片段库的速度
    all_jiasudu=[all_jiasudu;a_all]; %存储整个运动学片段库的加速度
    
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

3.12 计算整个运动学片段库的特征参数

%平均速度
var1=mean(all_chesu);
%平均行驶速度
var2=mean(all_chesu(all_chesu>10));
%平均加速度

a_all=all_jiasudu;
var3=mean(a_all(a_all>0))/3.6;
%平均减速度
var4=mean(a_all(a_all<0))/3.6;
%速度标准差
var5=std(all_chesu);
%加速度标准差
var6=std(a_all(a_all>0));
%减速度标准差
var7=std(a_all(a_all<0));
%怠速时间占比
var8=sum(all_chesu<10)/length(all_chesu);
%匀速时间占比
var9=sum(a_all==0)/length(a_all);
%加速时间占比
var10=sum(a_all>0)/length(a_all);
%减速时间占比
var11=sum(a_all<0)/length(a_all);
canshu_all_yundong=[var1 var2 var3 var4 var5 var6 var7 var8 var9 var10 var11];
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

3.13 平均相对误差

求出每个运动学片段与整个运动学片段库的特征参数的平均相对误差，以及每个运动学片段的长度，

%求出每个运动学片段与整个运动学片段库的特征参数的平均相对误差
yundong_chawu=[];
for i=1:size(tezheng,1)
    tem1=tezheng(i,:);
    yundong_chawu=[yundong_chawu;mean(abs((tem1-canshu_all_yundong)./canshu_all_yundong))];  
end

%求出每个运动学片段的长度
yundong_changdu=[];
for i=1:length(yundong)
    yundong_changdu=[yundong_changdu;length(yundong{i})];  
end

%将平均相对误差升序排序
[yundong_chawu_s,I_sort] = sort(yundong_chawu);
yundong_changdu_s = yundong_changdu(I_sort);

%将运动学片段长度累加
c_changdu=cumsum(yundong_changdu_s);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

3.14 暴力寻找最佳的运动学片段组合

根据上述求出的运动学片段长度累加值c_changdu可知，平均相对误差yundong_changdu_s的前7个最小的偏差对应的运动学片段的总长度小于1200秒，所以我们从前8个开始尝试，初始时q=8，逐渐增大q，在前q个运动学片段的所有排列组合中寻找总长度位于1200至1300秒之间的组合，即为误差最小的运动学片段组合。编制代码如下，

%寻找最为合适的运动学片段组合，
%该组合满足误差最小且时间之和为1200至1300之间
flag=1;
q=8;
while flag
    q=q+1;
    for p=1:q
        C = nchoosek(1:q,p);%从前q个数里找p个
        for i=1:size(C,1) %对于每一种组合来说
            tem1=yundong(I_sort(C(i,:)));
            tem1_changdu=[];
            for j=1:length(tem1)
                tem1_changdu=[tem1_changdu;length(tem1{j})];
            end
            
            %如果这种组合的时间总长度在1200至1300之间，则算找到合适的组合
            if (sum(tem1_changdu)>1200)&&(sum(tem1_changdu)<1300)
                find_ind=I_sort(C(i,:));
                flag=0;
                break;
            end
        end
        if flag==0
            break;
        end
    end
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

幸运的是，在q=8时，即找到了符合要求的运动学片段组合，即为如下7个片段，

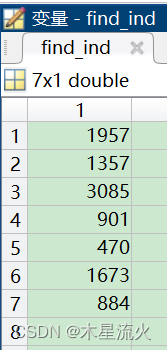
3.15 计算最佳组合的偏差

%计算找到的7个运动学片段的特征参数与整体运动学片段的差值

chesu_7=[];
jiasudu_7=[];
for i=1:7
    tem1=yundong{find_ind(i)};
    a_7=diff(tem1);
    a_7=[a_7(1);a_7];
    chesu_7=[chesu_7;tem1];
    jiasudu_7=[jiasudu_7;a_7];
end

%平均速度
var1=mean(chesu_7);
%平均行驶速度
var2=mean(chesu_7(chesu_7>10));
%平均加速度
var3=mean(jiasudu_7(jiasudu_7>0))/3.6;
%平均减速度
var4=mean(jiasudu_7(jiasudu_7<0))/3.6;
%速度标准差
var5=std(chesu_7);
%加速度标准差
var6=std(jiasudu_7(jiasudu_7>0));
%减速度标准差
var7=std(jiasudu_7(jiasudu_7<0));
%怠速时间占比
var8=sum(chesu_7<10)/length(chesu_7);
%匀速时间占比
var9=sum(jiasudu_7==0)/length(jiasudu_7);
%加速时间占比
var10=sum(jiasudu_7>0)/length(jiasudu_7);
%减速时间占比
var11=sum(jiasudu_7<0)/length(jiasudu_7);
tem2=[var1 var2 var3 var4 var5 var6 var7 var8 var9 var10 var11];
mean(abs((tem2-canshu_all_yundong)./canshu_all_yundong))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

最佳组合7个运动学片段的特征参数与整体运动学片段的相对误差为4.34%。

3.16 画出该最佳组合的运动学片段

op_yundong=[];
for i=1:7
    op_yundong=[op_yundong;yundong{find_ind(i)}];  
end
figure,plot(op_yundong);
1
2
3
4
5

3.17 总结

该题对数据预处理的考察力度较大。