k-近邻算法

k-近邻定义

• 定义：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。
  两个样本的距离可以通过如下公式计算，又叫欧式距离，比如说，a(a1,a2,a3),b(b1,b2,b3)
  

k-近邻算法

import pandas as pd
from sklearn.model_selection import  train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier

def knncls():
    '''
    K—近邻预测用户签到位置
    :return:None
    '''
    #读取数据
    data=pd.read_csv('./data/FBlocation/train.csv')
    #处理数据
    #1.缩小数据，查询数据筛选
    data.query('x>1.0 & x<1.25 & y>2.5 & y<2.75')  #data.query()查询语句，data是DataFrame
    #2.处理时间数据
    time_value=pd.to_datetime(data['time'],unit='s')
    #3.将日期函数转换为字典
    time_value=pd.DatetimeIndex(time_value)
    #3.构造一些特征
    data['day']=time_value.day
    data['hour']=time_value.hour
    data['weekday']=time_value.weekday
    #4.删除时间戳特征
    data=data.drop(['time'],axis=1)  #sklearn中0表示列,pandas在1表示列
    #将签到数量少于n个目标位置删除
    place_count = data.groupby('place_id').count()#按照place_id将数据分组，再求和，索引为place_count
    tf = place_count[place_count.row_id > 3].reset_index()#reset_index()将place_count重新变为一列，索引就变为0，1，2……
    data = data[data['place_id'].isin(tf.place_id)]
    #取出数据当中的特征值和目标值
    y=data['place_id']
    x=data.drop(['place_id'],axis=1)

    #进行数据的分割训练集和测试集
    x_train, x_test, y_train, y_test=train_test_split(x,y,test_size=0.25)

    #特征工程（对特征值进行标准化）
    std=StandardScaler()
    x_train=std.fit_transform(x_train)
    x_test=std.transform(x_test)  #不需要fit，因为上面已经计算了均值和标准差
    #进行算法流程
    knn=KNeighborsClassifier(n_neighbors=5)

    #fit predict score
    knn.fit(x_train,y_train)
    #得出预测结果
    y_predict=knn.predict(x_test)
    print('预测的目标签到位置：',y_predict)
    #得出准确率
    print('预测的准确率',knn.score(x_test,y_test))
if __name__=='__main__':
    knncls()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

k-近邻的优缺点

（1）k值大小
k值取很小：容易受异常点影响
k值取很大：容易受最近数据太多导致比例变化
（2）优缺点：
优点：简单，易于理解，易于实现，无需估计参数，无需训练
缺点：懒惰算法，对测试样本分类时的计算量大，内存开销大；必须指定K值，K值选择不当则分类精度不能保证。
使用场景：小数据场景，几千～几万样本，具体场景具体业务去测试。
k-近邻算法实现：加快搜索速度——基于算法的改进KDTree,API接口里面有实现

朴素贝叶斯

相关知识点

• 联合概率：包含多个条件，且所有条件同时成立的概率记作：P(A,B)
  特性：P(AB)=P(A)P(B)
• 条件概率：就是事件A在另外一个事件B已经发生条件下的发生概率，记作：P(A|B)
  特性：P(A1,A2|B) = P(A1|B)P(A2|B)
  注意：此条件概率的成立，是由于A1,A2相互独立的结果（即“朴素”）
• 朴素贝叶斯-贝叶斯公式
  

拉普拉斯平滑系数：
问题：从上面的例子我们得到娱乐概率为0，这是不合理的，如果词频列表里面有很多出现次数都为0，很可能计算结果都为零。
解决方法：拉普拉斯平滑系数

朴素贝叶斯算法

从 sklearn.naive_bayes中导入MultinomialNB
sklearn.naive_bayes.MultinomialNB(alpha = 1.0)

from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
def naviebayes():
    '''
    朴素贝叶斯进行文本分类
    :return:
    '''
    news=fetch_20newsgroups(subset='all')
    #进行数据分割(特征值、目标值)
    x_train,x_test,y_train,y_test=train_test_split(news.data,news.target,test_size=0.25)
    #对数据集进行特征抽取
    tf=TfidfVectorizer()
    #以训练集当中的词的列表进行每篇文章重要性的统计
    x_train=tf.fit_transform(x_train)
    x_test=tf.transform(x_test)
    #进行朴素贝叶斯算法的预测
    mlt=MultinomialNB(alpha=1.0)
    mlt.fit(x_train,y_train)
    y_predict=mlt.predict(x_test)
    print('预测文章类别为：',y_predict)
    print('准确率为：',mlt.score(x_test,y_test))
if __name__=='__main__':
    naviebayes()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

朴素贝叶斯的优缺点

（1）优点：
朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。
对缺失数据不太敏感，算法也比较简单，常用于文本分类。
分类准确度高，速度快
（2）缺点
需要知道先验概率P(F1,F2,…|C)，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
由于是假设相互独立，所以出现相关的话效果就不好。

分类模型的评估

• estimator.score()一般最常见使用的是准确率，即预测结果正确的百分比

混淆矩阵

• 在分类任务下，预测结果(Predicted Condition)与正确标记(True Condition)之间存在四种不同的组合，构成混淆矩阵(适用于多分类)。
  

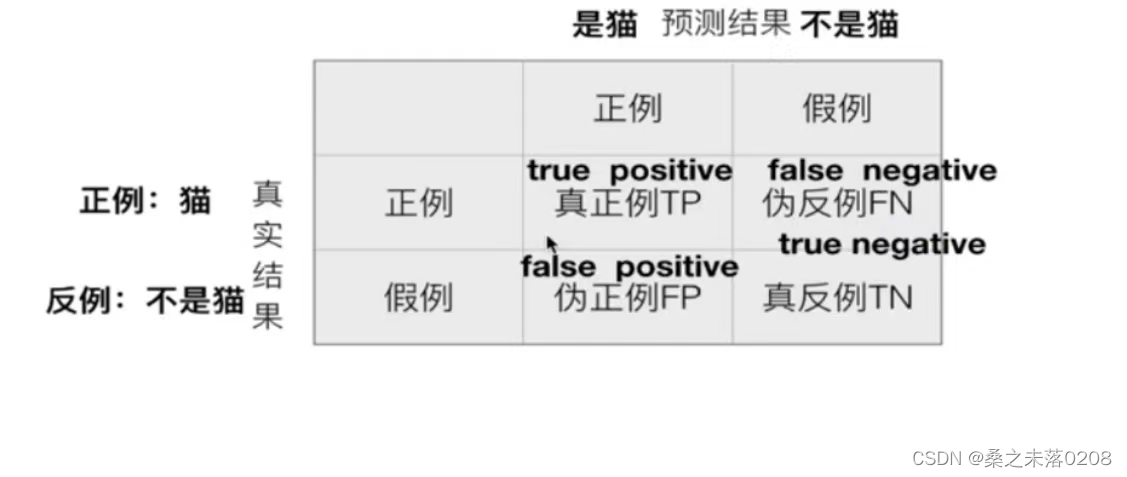
评估标准

为精确率(Precision)和召回率(Recall)
精确率（了解即可）：预测结果为正例样本中真实为正例的比例（查得准）

召回率（熟悉）：真实为正例的样本中预测结果为正例的比例（查的全，对正样本的区分能力）TP/(TP+FN)

分类模型评估API

从sklearn.metrics导入classification_report
sklearn.metrics.classification_report(y_true, y_pred, target_names=None)
y_true：真实目标值
y_pred：估计器预测目标值
target_names：目标类别名称
return：每个类别精确率与召回率

from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import classification_report
def naviebayes():
'''
    朴素贝叶斯进行文本分类
    :return:
    '''
    news=fetch_20newsgroups(subset='all')
    #进行数据分割(特征值、目标值)
	x_train,x_test,y_train,y_test=train_test_split(news.data,news.target,test_size=0.25)
    #对数据集进行特征抽取
    tf=TfidfVectorizer()
    #以训练集当中的词的列表进行每篇文章重要性的统计
    x_train=tf.fit_transform(x_train)
    x_test=tf.transform(x_test)
    #进行朴素贝叶斯算法的预测
    mlt=MultinomialNB(alpha=1.0)
    mlt.fit(x_train,y_train)
    y_predict=mlt.predict(x_test)
	#查看精确率和召回率
	print('精确率、召回率为：',classification_report(y_test,y_predict,target_names=news.target_names))
if __name__=='__main__':
    naviebayes()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

模型选择与调优

交叉验证过程

交叉验证：将拿到的数据，分为训练和验证集。以下图为例：将数据分成5份，其中一份作为验证集。然后经过5次(组)的测试，每次都更换不同的验证集。即得到5组模型的结果，取平均值作为最终结果。又称5折交叉验证。

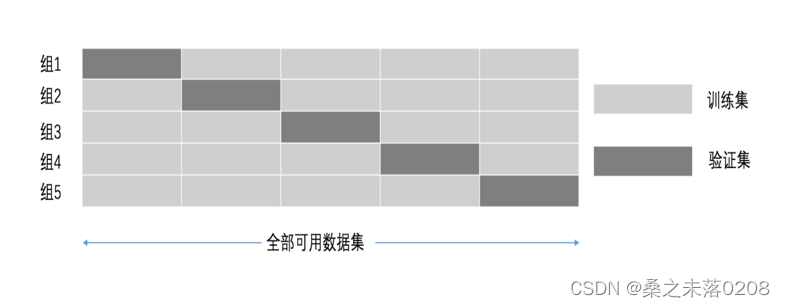
超参数搜索-网格搜索

通常情况下，有很多参数是需要手动指定的（如k-近邻算法中的K值），这种叫超参数。但是手动过程繁杂，所以需要对模型预设几种超参数组合。每组超参数都采用交叉验证来进行评估。最后选出最优参数组合建立模型。
使用GridSearchCV：
sklearn.model_selection.GridSearchCV(estimator, param_grid=None,cv=None)
对估计器的指定参数值进行详尽搜索
estimator：估计器对象
param_grid：估计器参数(dict){“n_neighbors”:[1,3,5]}
cv：指定几折交叉验证
fit：输入训练数据
score：准确率
结果分析：
best_score_:在交叉验证中测试的最好结果
best_estimator_：最好的参数模型
cv_results_:每次交叉验证后的测试集准确率结果和训练集准确率结果

from sklearn.model_selection import GridSearchCV
def knncls():
    '''
    K—近邻预测用户签到位置
    :return:None
    '''
    #读取数据
    data=pd.read_csv('./data/FBlocation/train.csv')
    
    #处理数据
    #1.缩小数据，查询数据筛选
    data.query('x>1.0 & x<1.25 & y>2.5 & y<2.75')  #data.query()查询语句，data是DataFrame
    #2.处理时间数据
    time_value=pd.to_datetime(data['time'],unit='s')
    #3.将日期函数转换为字典
    time_value=pd.DatetimeIndex(time_value)
    #3.构造一些特征
    data['day']=time_value.day
    data['hour']=time_value.hour
    data['weekday']=time_value.weekday
    #4.删除时间戳特征
    data=data.drop(['time'],axis=1)  #sklearn中0表示列,pandas在1表示列
    #将签到数量少于n个目标位置删除
    place_count = data.groupby('place_id').count()#按照place_id将数据分组，再求和，索引为place_count
    tf = place_count[place_count.row_id > 3].reset_index()#reset_index()将place_count重新变为一列，索引就变为0，1，2……
    data = data[data['place_id'].isin(tf.place_id)]
    #取出数据当中的特征值和目标值
    y=data['place_id']
    x=data.drop(['place_id'],axis=1)

    #进行数据的分割训练集和测试集
    x_train, x_test, y_train, y_test=train_test_split(x,y,test_size=0.25)

    #特征工程（对特征值进行标准化）
    std=StandardScaler()
    x_train=std.fit_transform(x_train)
    x_test=std.transform(x_test)  #不需要fit，因为上面已经计算了均值和标准差

    #进行算法流程
    knn=KNeighborsClassifier()

    #构造一些参数的值进行搜素
    param={"n_neighbors":[3,5,10]}
    #进行网格搜索
    gc=GridSearchCV(knn,param_grid=param,cv=2)
    gc.fit(x_train,y_train)
    #预测准确率
    print('在测试集上的准确率：',gc.score(x_test,y_test))
    print('在交叉验证中最好的结果：',gc.best_score_)
    print('选择最好的模型：',gc.best_estimator_)
    print('每个超参数每次交叉验证的结果：',gc.cv_results_)
if __name__=='__main__':
    knncls()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53