堆-堆排序-TopK

大堆：父节点比左右子孩子大
小堆：父节点比左右子孩子小

---

大堆向下调整

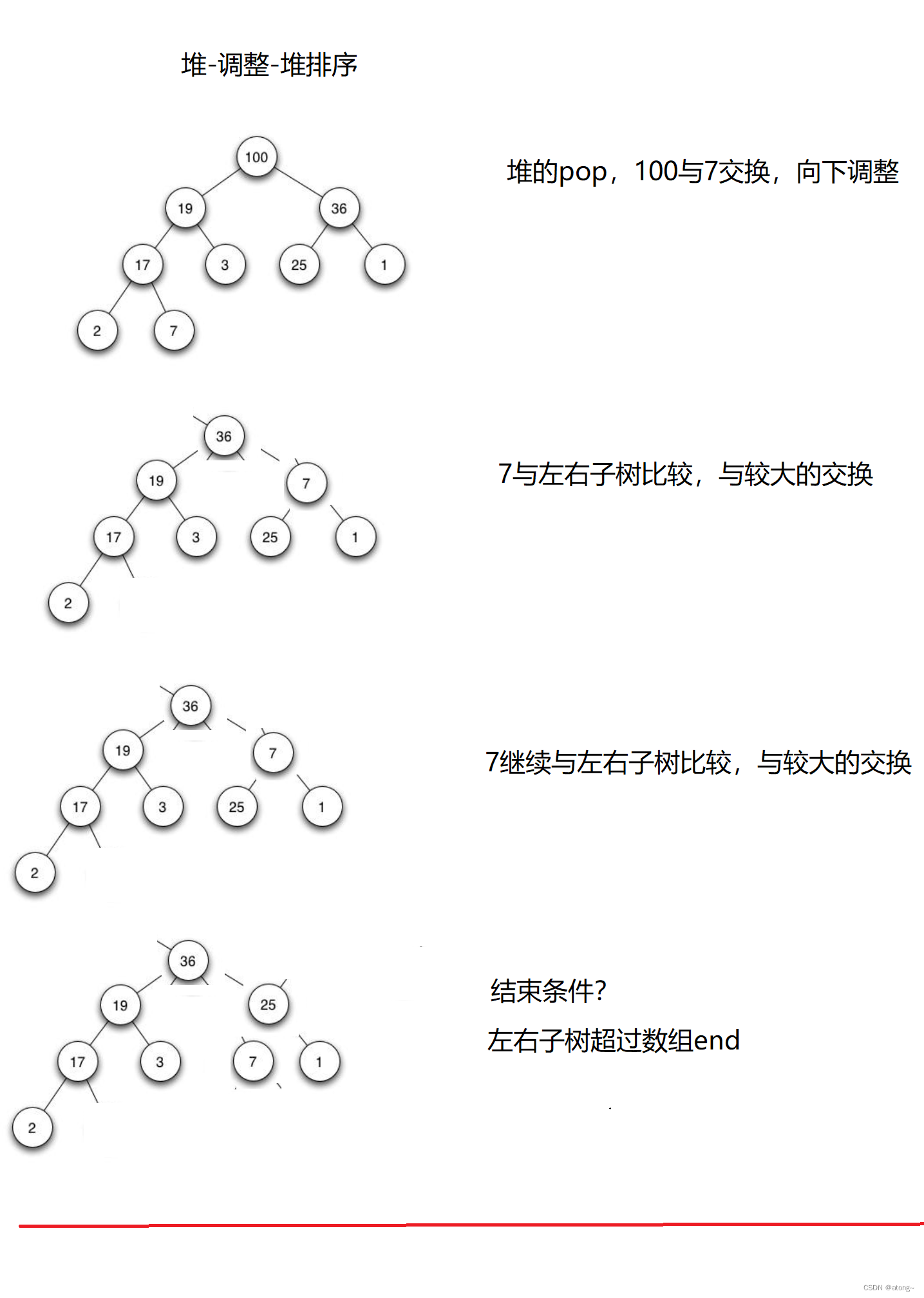
向下调整算法

注意结束

1. 是左右子树超过数组end
2. 到了合适位置直接break出去

问题：end是数组元素个数还是最后一个元素所在下标？
最后一个元素所在下标

错误代码1、

void AdjustDown(int* a, int n)
{
    assert(a);
    int parent=0;
    int left=2*parent+1;
   	int right=left+1;
    while(left<end)
    {
        left=2*parent+1;
   		right=left+1;
		if(a[left]>a[right])
        {
             Swap(&a[parent],&a[left]);
             parent=left;
        }
        else
        {
             Swap(&a[parent],&a[right]);
             parent=right;
        }
    }
    
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

更正代码2

void AdjustDown(int* a, int n)
{
    assert(a);
    int parent=0,left=0,right=0;
    while(left<end)
    {
        left=2*parent+1;
   		right=left+1;
		if(a[left]>a[right])
        {
             if(a[parent]<a[left])
             {
                 Swap(&a[parent],&a[left]);
            	 parent=left;
             }
             else
             {
             	break;   
             }
             
        }
        else
        {
             if(a[parent]<a[right])
             {
                 Swap(&a[parent],&a[right]);
            	 parent=right;
             }
             else
             {
             	break;   
             }
        }
    }
    
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

最终代码3

//建大堆
void AdjustDown(int* a, int n, int parent)
{
    int child=parent*2+1;
    while(child<end)
    {
		if(child+1<n&&a[child+1]>a[child+1])
        {
			child=child+1;
        }
        if(a[child]>a[parent])
        {
            Swap[&a[parent],&a[child]);
            parent=child;
            child=2*parent+1;
        }
        else
        {
            break;
        }
                
    }
    
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

大堆向上调整

向上调整算法

1. 结束条件：child<=0;
2. 在end处插入一个元素，与父节点向上比较，孩子大就调换，孩子不大于父亲就break

代码 大堆

void AdJustUp(int* a, int child)
{
    int parent=(child-1)/2;
    while(child>0)
    {
        if(a[child]>a[parent])
        {
            Swap[&a[child],&a[parent]);
            child=parent;
            parent=(child-1)/2;  
        }
        else
        {
         	break;            
        }
                    
                      
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

建堆-时间复杂度分析

1、向下建堆

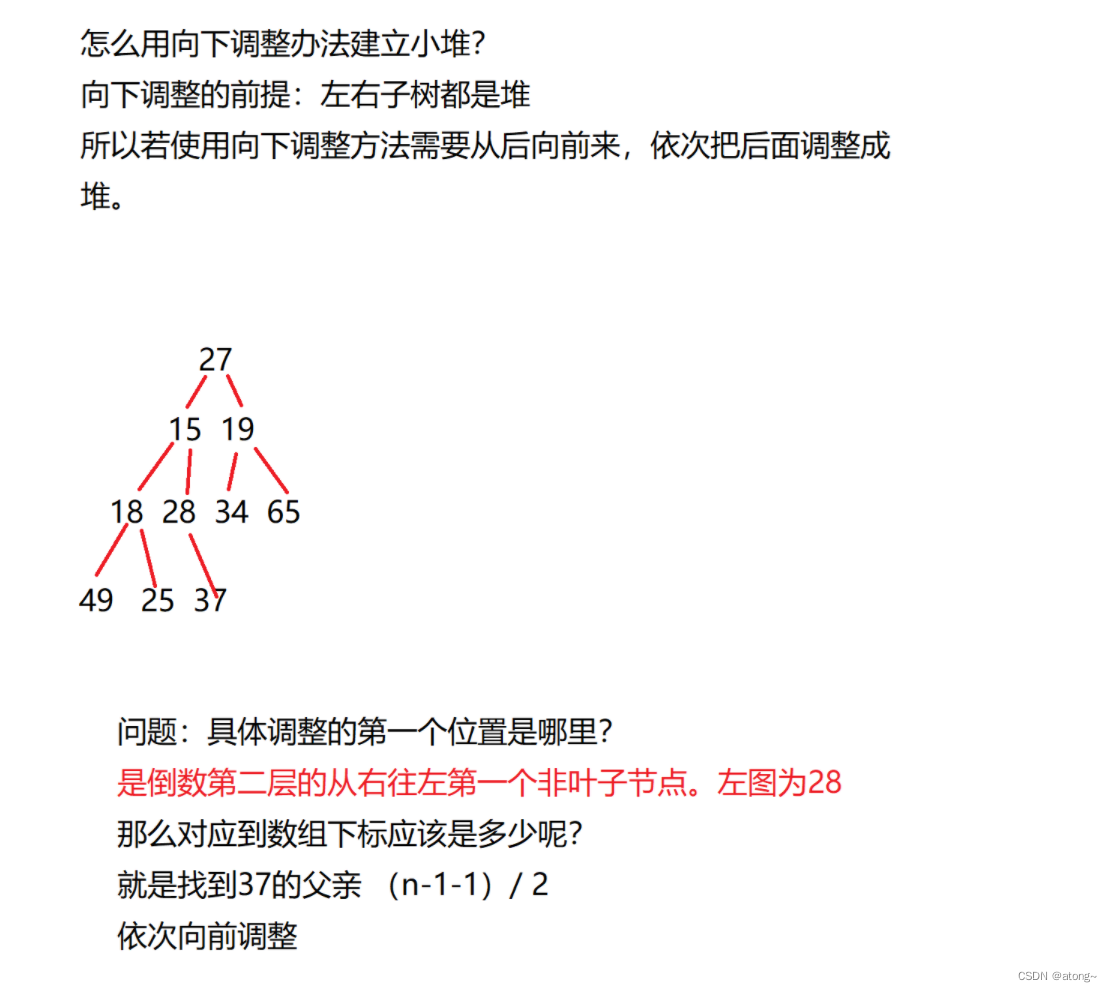
代码：向下调整算法

 //向下调整
    for(int i=(n-1-1)/2;i>=0;i--)
    {
        AdJustDown(a, n, i);
    }
1
2
3
4
5

时间复杂度分析（向下调整）

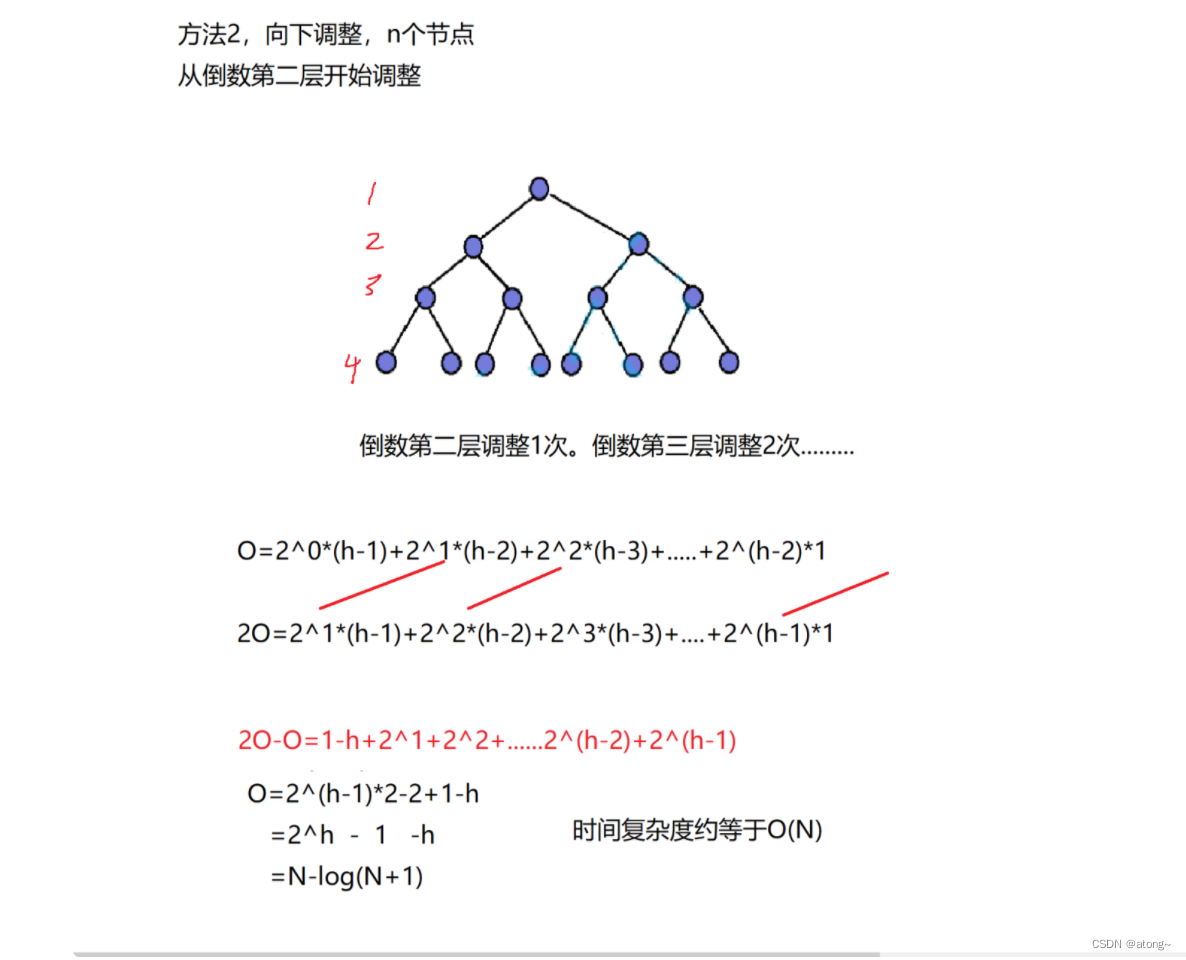
2、向上建堆

代码：向上调整算法

 // 向上调整
  for(int i=0;i<sizeof(a)/sizeof(int);i++)
  {
       AdJustUp(a,i);
  }
1
2
3
4
5

建堆复杂度分析（向上调整）

---

atong知识分享-TopK问题

1、如何在n个数中选出前K大/小的数

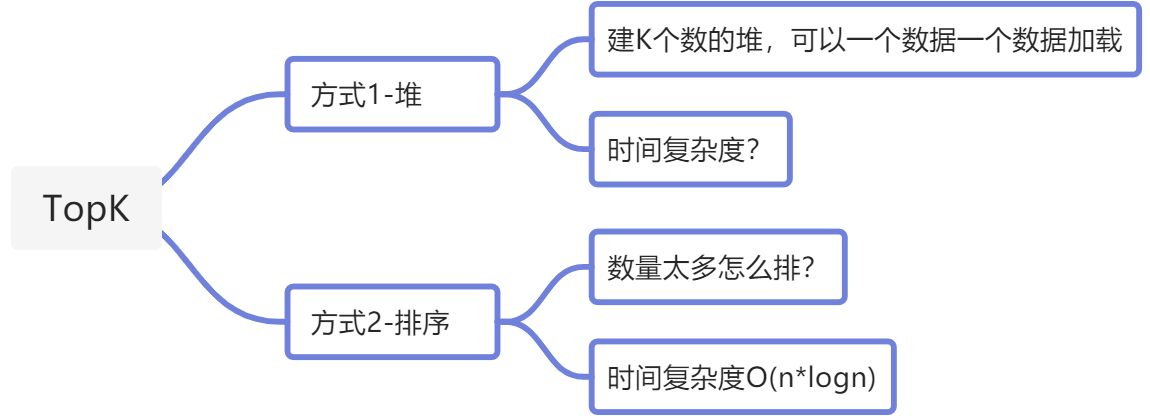
2、堆实现

N个数，选出前K大的数(建小堆-小堆堆顶)

分析

建小堆，a[i]大于堆顶，交换向下调整，大的会往下调整到堆底，小数往上冒，当i遍历到N时，堆顶就是第K大的元素

3、时间复杂度分析

1. 建k个数堆时间复杂度

向下调整建堆K个数：O(K)

2. 后边数据比较调整

最坏情况，N个数从小到大排，从K+1个数开始，每个数都比堆顶元素大，K个元素有logK层，每个数调整logK次，都调整到堆底时间复杂度为：O((N-K)*logK)

*总体时间复杂度：O(K+(N-K)logK)

4、代码实现

void TestTopK(int* a, int n, int k)
{
    //建堆K个数 a[k-1] 它的父亲是(k-1-1)/2  向下调整建堆
    for(int i=(k-1-1)/2;i>=0;i--)
    {
        AdJustDown(a, k, i);
    }
    /*
    若不破坏原数组
    int* MinHeap = (int*)malloc(sizeof(int)*k);
	assert(MinHeap);
	for (int i = 0; i < k; ++i)
	{
		MinHeap[i] = a[i];
	}
	for (int i = (k - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDwon(kMinHeap, k, i);
	}
    */
    for(int i=k+1; i<n, i++)
    {
        if(a[i]>a[0])
        {
            Swap(&a[0], &a[i]);
            AdJustDown(a, k, 0);
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29