我的数据结构与算法「图」

图

图是描述于一组对象的结构，其中某些对象对在某种意义上是相关的。这些对象的数学抽象称为顶点的（也称结点或点），并且每个相关的顶点对都称为边（也称为链接或线）

图的基本概念

• 图的定义

  $G$ 由顶点集 $V$ 和边集 $E$ 组成，记为 $G=(V,E)$

  1. $V(G)$ 表示图 $G$ 中顶点的有限非空集，若 V = { v 1 , v 2 , ⋯   , v n } V=\{v_1,v_2,\cdots,v_n\} V={v1​,v2​,⋯,vn​} 则用 $|V|$ 表示图 $G$ 中顶点的个数，也称为图 $G$ 的阶
  2. $E(G)$ 表示图 $G$ 中顶点之间边（关系）的集合，若 E = { ( u ， v ) ∣ u ∈ V , v ∈ V } E=\{(u，v)\mid u \in V, v \in V\} E={(u，v)∣u∈V,v∈V} 则用 $|E|$ 表示图 $G$ 中边的条数

  树是图的子集，是一种特殊的图，定义是 $n,(n\ge 0)$ 个结点的有限集合，$n=0$ 时称为空树，而任意一棵非空树中应满足

  1. 有且仅有一个特定的称为根的结点
  2. 当 $n>1$ 时，其余结点可分为 $m(m>0)$ 个互不相交的有限集合 $T_1,T_2,\cdots ,T_m$，其中每一个集合本身又是一棵树，称为根结点的子树

• 图的分类

  1. 无向图

     $E$ 无向边的有限集合，边是顶点的无序对，记为 $(v,w)$ 且 $(v,w)=(w,v)$，称 $w,v$ 互为邻接点

  2. 有向图

     $E$ 是有向边（弧）的有限集合，弧是顶点的有序对，记为 $<v,w>$，$v$ 是弧尾，$w$ 是弧头，称 $v$ 邻接到 $w$ 或 $w$ 邻接自 $v$

  3. 简单图

     不存在顶点到自身的边，同一条边不重复出现

  4. 多重图

     与简单图相对，某两个结点之间的边数多于一条，且允许顶点通过通过同一个边和自己关联

  5. 完全图

     • 无向完全图，任意两个顶点之间都存在边
     • 有向完全图，任意两个顶点之间都存在方向相反的两条弧

  6. 子图

     设有两个图 $G=(V,E)$ 和 $G^{\prime }=(V^{\prime },E^{\prime })$ 若 $V^{\prime }$ 是 $V$ 的子集，且 $E^{\prime }$ 是 $E$ 的子集，则称 $G^{\prime }$ 是 $G$ 的子图。若有满足 $V(G^{\prime })=V(G)$ 的子图 $G^{\prime }$，则称其为 $G$ 的生成子图

     并非 $V$ 和 $E$ 的任何子集都能构成 $G$ 的子图，因为这样的子集可能不是图，即 $E$ 的子集中的某些边关联的顶点可能不在这个 $V$ 的子集中

  7. 连通图

     在无向图中，若从顶点 $v$ 到顶点 $w$ 有路径存在，则称 $v$ 和 $w$ 是连通的。若图 $G$ 中任意两个顶点都是连通的，则称图 $G$ 为连通图，如果一个图有 $n$ 个顶点，并且有小于 $n-1$ 条边称为非连通图

     • 连通分量

       无向图中的极大连通子图，即选取一个顶点，以这个顶点作为一个子图，然后逐个添加与这个子图相连的顶点和边直到所有相连的顶点都加入该子图

     • 强连通图

       在有向图中，若顶点 $v$ 到顶点 $w$ 和顶点 $w$ 到顶点 $v$ 都有路径则这两个顶点称为强连通。若 $G$ 图中任一对顶点都是强连通的，则称图 $G$ 为强连通图

  8. 连通图的生成树

     包含图中全部 $n$ 个顶点，但是只有 $n-1$ 条边的极小连通子图，对于该生成树而言，去掉一条边则变成非连通图，加上一条边就会形成回路

  9. 顶点的度

     以顶点为一个端点的边数目

     • 无向图中顶点 $v$ 的度是指依附于该顶点的边的条数，记为 $TD(v)$
     • 有向图中顶点 $v$ 的度分为出度 $ID$ 以顶点 $v$ 为起点的有向边的数目，入度 $OD$ 以顶点 $v$ 为终点的有向边的数目

  10. 边的权和网

      图中每条边都可以赋予一定意义的数值，这个数值叫做这条边的权，有权值得图称为带权图，也叫做网

  11. 路径、路径长度和回路

      顶点 $v_p$ 到 $v_q$ 之间的路径是指顶点序列 $v_p,v_{i_1},v_{i_2},\cdots ,v_{i_m},v_q$，路径上边的数目就是路径长度，第一个和最后一个顶点相同的路径称为回路或者环

      若一个图有 $n$ 个顶点，并且有大于 $n-1$ 条边则此图必有环

      • 简单路径

        顶点不重复出现的路径

      • 简单回路

        除了第一个和最后一个顶点其余顶点不重复出现的回路

  12. 距离

      从顶点 $u$ 到 $v$ 的最短路径长度为其距离。不存在路径，则记距离为无穷 $\infty$

图的存储结构

• 顺序存储

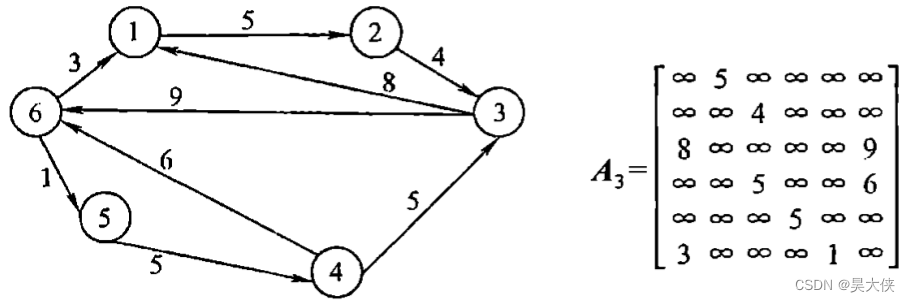
  邻接矩阵，是指用一个一维数组存储图中顶点的信息，用一个二维数组存储图中边的信息即各顶点之间的邻接关系，存储顶点之间邻接关系的二维数组称为邻接矩阵

  结点数为 $n$ 的图 $G=(V,E)$ 的的邻接矩阵 $A$ 是 $n\times n$ 的。将 $G$ 的顶点编号为 $v_1,v_2,\cdots ,v_n$，若$(v_i,v_j)\in E$，则 $A[i][j]=1$，否则 $A[i][j]=0$。若为带权图，$v_i$ 与 $v_j$ 有边连接则邻接矩阵中存放边的权值 $A[i][j]=w_{ij}$ 否则 $A[i][j]=\infty$

  

• 顺序存储与链式存储

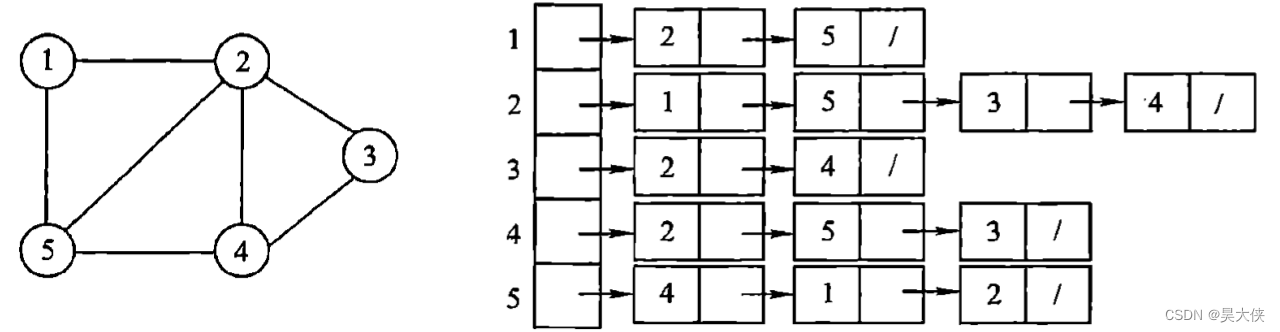
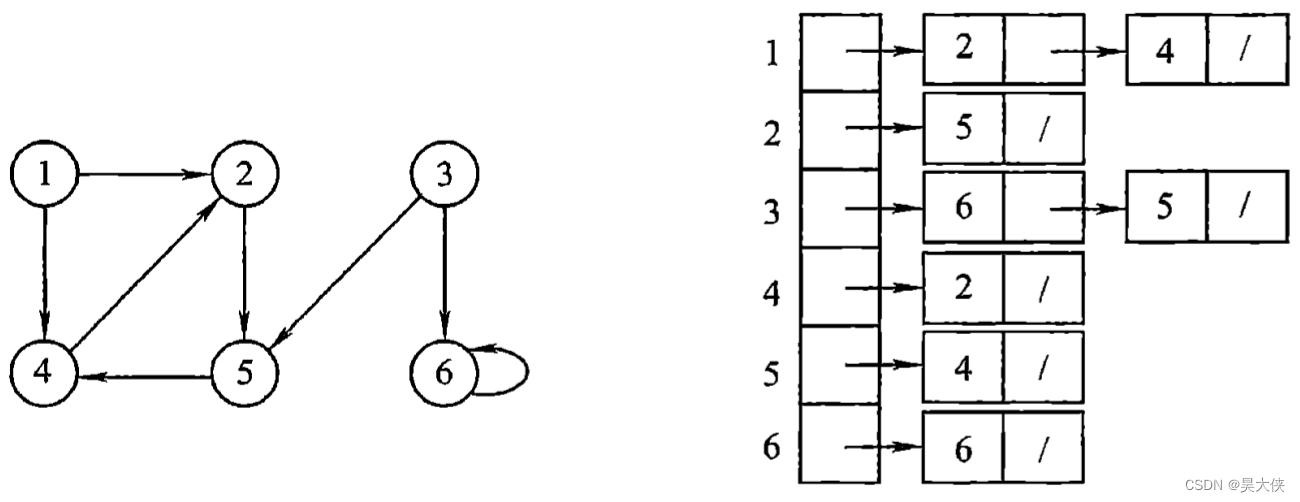
  邻接表，是指对图 $G$ 中的每个顶点以 $v_i$ 建立一个单链表，第 $i$ 个单链表中的结点表示依附于顶点 $v_i$ 的边（对于有向图则是以顶点 $v_i$ 为尾的弧），这个单链表就称为顶点 $v_i$ 的边表（对于有向图则称为出边表）。边表的头指针与顶点的数据信息采用顺序存储，称为顶点表，所以在邻接表中存在两种结点，顶点表结点与边表结点

  

• 链式存储

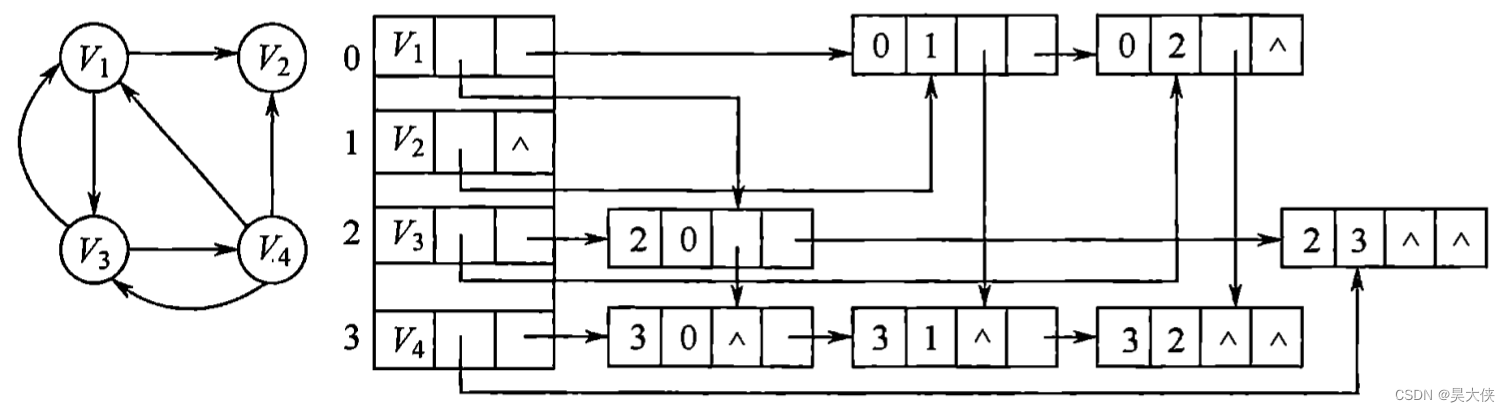
  1. 十字链表用于存储有向图，对应于有向图中的每条弧有一个弧结点，其中有 $5$ 个域：尾域（tailvex）和头域（headvex）分别指示弧尾和弧头这两个顶点在图中的位置：两个链域 （hlink 与 tlink）分别指向弧头相同的下一条弧与弧尾相同的下一条弧；信息域（info）指向该弧的相关信息。弧头相同的弧就在同一个链表上，弧尾相同的弧也在同个链表上。对应于每个顶点也有一个结点，顶点结点中有 $3$ 个域，数据域（data）存放顶点相关的数据信息，如顶点名称；两个链域（firstin 与 firstout）分别指向以该顶点为弧头与弧尾的第一个弧结点

     

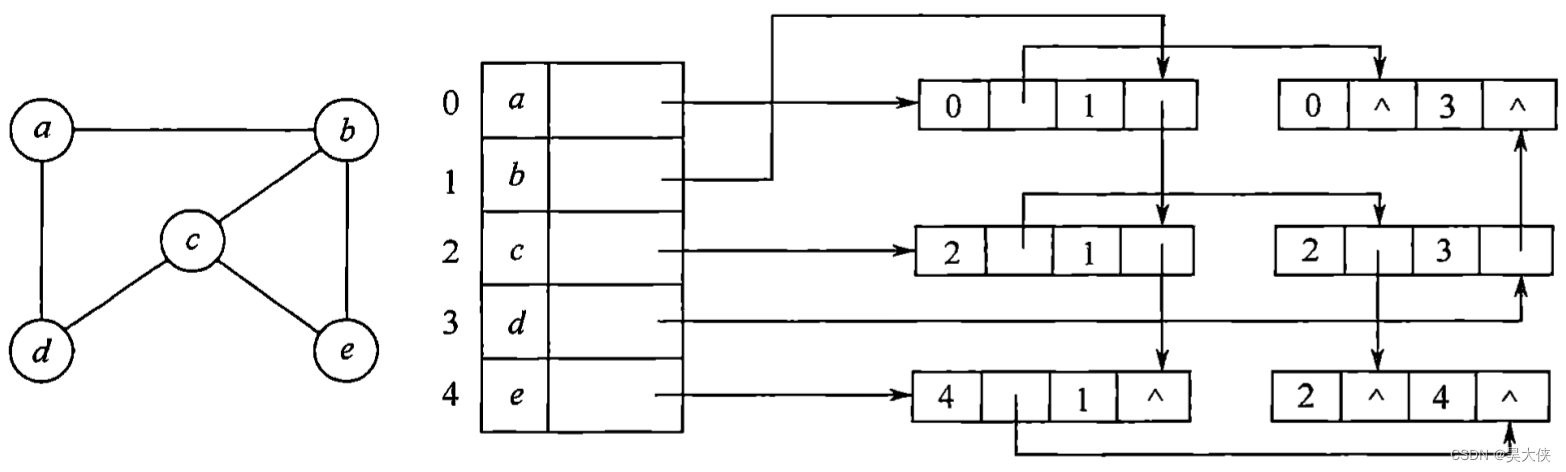
  2. 邻接多重表用于存储无向图，与十字链表类似，每条边用一个结点表示，边结点包含六个域，其中标志域（mark）表示边是否被搜索过，两个位置域（ivex 与 jvex）分别表示该边依附的两个顶点在图中的位置，两个链域（ilink 与 jlink）分别指向下一条依附于相应顶点的边地址，信息域（info）指向和边相关的各种信息。对应于每个顶点也有一个结点，顶点结点中有 $2$ 个域，数据域（data）存放顶点相关的数据信息；链域（firstedge）指向第一个依附该顶点的边

     

• 基本操作

  例如，判断、插入、删除和数边等操作都独立于图的存储结构，对于不同的存储方式，操作算法的具体实现的性能不同。在设计具体算法的实现时，应考虑采用何种存储方式的算法效率会更高

图的遍历

• 深度优先遍历

  即深度优先搜索（DFS，Depth-First-Search）类似于树的先序遍历算法，故也适用于树，首先访问图中某一起始顶点 $v$，然后由 $v$ 出发，访问与 $v$ 邻接且末被访问的任一顶点 $w_1$，再访问与 $w_1$ 邻接且未被访问的任一顶点 $w_2,\cdots$ 重复上述过程，一条路径一直走到底。当不能再继续向下访问时，进行回溯，依次退回到最近被访问的顶点，若它还有邻接顶点未被访问过，则从该点开始继续上述搜索过程，直至图中所有顶点均被访问过为止

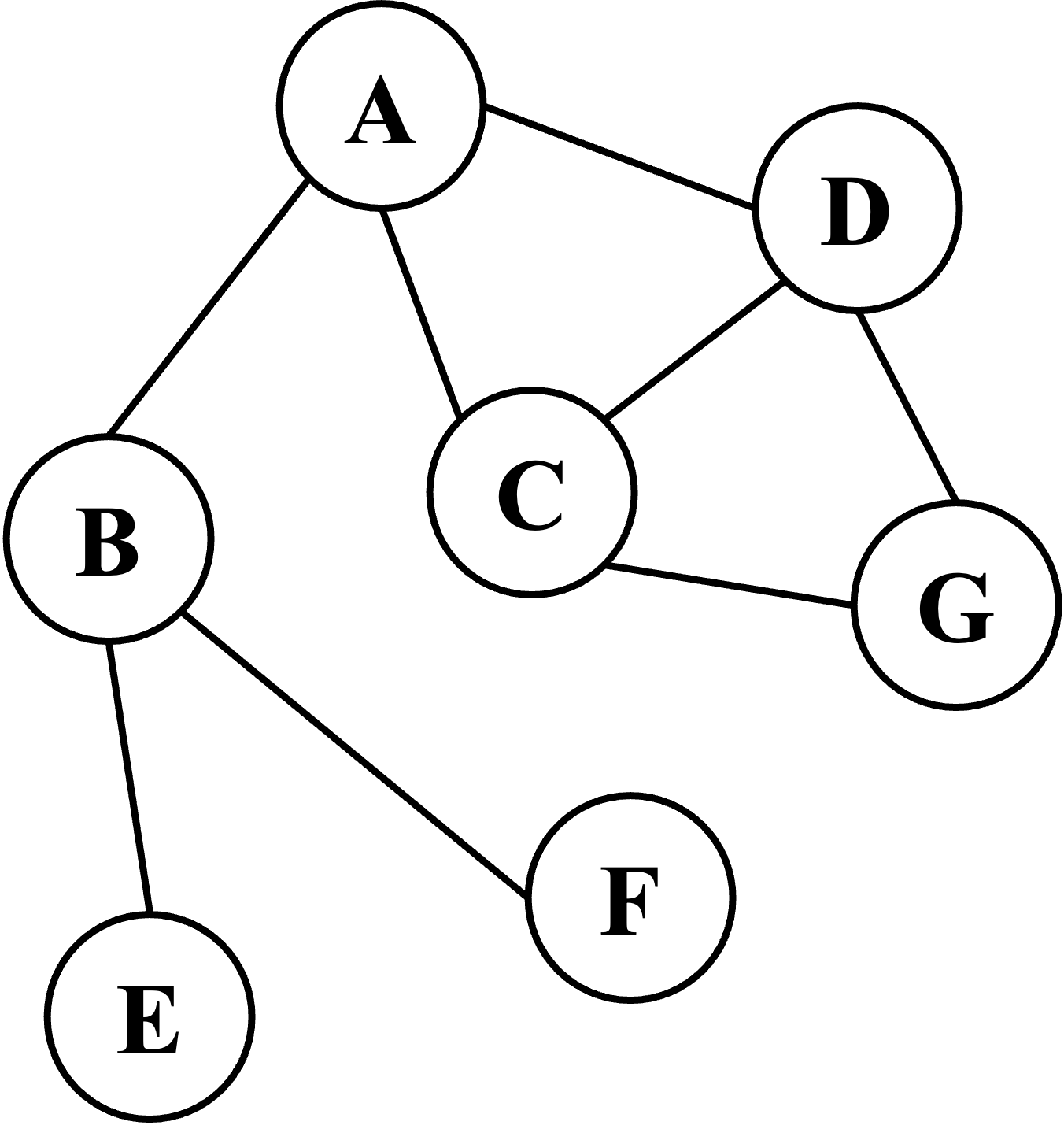
  1. 举例

     算法逻辑

     1. 首先，创建一个空堆栈 $stack$（用来存放结点）和一个空列表 $visit$（用来存放已访问的结点）
     2. 其次，从 $v_A$ 开始， $v_A$ 压入堆栈，此时 v i s i t = { ∅ } , q u e u e = { v A } visit=\{\emptyset\},queue=\{v_A\} visit={∅},queue={vA​}
     3. 当 $v_A$ 推出堆栈时 v i s i t = { v A } visit=\{v_A\} visit={vA​}，$v_A$ 的邻接结点 $v_B,v_C,v_D$ 压入堆栈，此时 s t a c k = { v B , v C , v D } stack=\{v_B,v_C,v_D\} stack={vB​,vC​,vD​}
     4. 接着堆栈尾 $v_D$ 推出堆栈，此时 v i s i t = { v A , v D } visit=\{v_A,v_D\} visit={vA​,vD​}，$v_D$ 的邻接结点中 $v_A,v_C,v_G$ 中未压入堆栈的 $v_G$ 压入堆栈，此时 s t a c k = { v B , v C , v G } stack=\{v_B,v_C,v_G\} stack={vB​,vC​,vG​}
     5. 然后堆栈尾 $v_G$ 推出堆栈，此时 v i s i t = { v A , v D , v G } visit=\{v_A,v_D,v_G\} visit={vA​,vD​,vG​}，$v_G$ 的邻接结点中 $v_C,v_D$ 已经全部压入过堆栈的故不再压栈 ，此时 s t a c k = { v B , v C } stack=\{v_B,v_C\} stack={vB​,vC​}
     6. 再然后堆栈尾 $v_C$ 推出堆栈，此时 v i s i t = { v A , v D , v G , v C } visit=\{v_A,v_D,v_G,v_C\} visit={vA​,vD​,vG​,vC​}，$v_C$ 的邻接结点中 $v_A,v_D,v_F,v_G$ 中未压入堆栈的 $v_F$ 压入堆栈，此时 s t a c k = { v B , v F } stack=\{v_B,v_F\} stack={vB​,vF​}
     7. 再然后堆栈尾 $v_F$ 推出堆栈，此时 v i s i t = { v A , v D , v G , v C , v F } visit=\{v_A,v_D,v_G,v_C,v_F\} visit={vA​,vD​,vG​,vC​,vF​}，$v_F$ 的邻接结点中 $v_B,v_C$ 已经全部压入过堆栈的故不再压栈，此时 s t a c k = { v B } stack=\{v_B\} stack={vB​}
     8. 再然后堆栈尾 $v_B$ 推出堆栈，此时 v i s i t = { v A , v D , v G , v C , v F , v B } visit=\{v_A,v_D,v_G,v_C,v_F,v_B\} visit={vA​,vD​,vG​,vC​,vF​,vB​}，$v_B$ 的邻接结点中 $v_A,v_E,v_F$ 中未压入堆栈的 $v_E$ 压入堆栈，此时 s t a c k = { v E } stack=\{v_E\} stack={vE​}
     9. 最后 $v_E$ 结点压出堆栈直到 s t a c k = { ∅ } , v i s i t = { v A , v D , v G , v C , v F , v B , v E } stack=\{\emptyset\},visit=\{v_A,v_D,v_G,v_C,v_F,v_B,v_E\} stack={∅},visit={vA​,vD​,vG​,vC​,vF​,vB​,vE​}

     算法实现

     # 用字典结构表示图的邻接表
     graph_nt = {
         'A' : ['B','C','D'],
         'B' : ['A','E','F'],
         'C' : ['A','D','F','G'],
         'D' : ['A','C','G'],
         'E' : ['B'],
         'F' : ['B','C'],
         'G' : ['C','D']
     }
     
     def DFS(start, graph):
         stack = []
         visit = []
         stack.append(start)
         while stack:
             node = stack.pop()
             visit.append(node)
             nodes = graph[node]
             for i in nodes:
                 if i not in visit:
                     stack.append(i)
                     visit.append(i)
             print(node,end='\t')
     
     DFS(start='A', graph=graph_nt)
     1
     2
     3
     4
     5
     6
     7
     8
     9
     10
     11
     12
     13
     14
     15
     16
     17
     18
     19
     20
     21
     22
     23
     24
     25
     26

  2. 空间复杂度

     由于 DFS 是一个递归算法，需要一个工作栈来辅助工作，最多需要图中所有顶点进栈，所以空间复杂度为 $O(|V|)$

  3. 时间复杂度

     邻接矩阵，查找每个顶点的邻接点时间复杂度为 $O(|V|)$，对每个顶点都进行查找，所以总的时间复杂度为 $O(|V{|}^2)$

     邻接表，遍历过程的主要操作是对顶点遍历它的邻接点，由于通过访问边表来查找邻接点，所以时间复杂度为 $O(|E|)$，访问顶点时间为 $O(|V|)$，所以总的时间复杂度为 $O(|V|+|E|)$

• 广度优先遍历

  即广度优先搜索（BFS，Breadth-First-Search）似于树的层序遍历算法，故也适用于树，其过程是以 $v$ 为起始点，由近至远依次访问和 $v$ 有路径相通且路径长度为 $1,2,\cdots$ 的顶点，广度优先搜索是一种分层的查找过程，每向前走一步可能访问一批顶点，不像深度优先搜索那样有往回退的情况，它不是一个递归的算法。为了实现逐层的访问，算法必须借助一个辅助队列，以记忆正在访问的顶点的下一层顶点

  1. 举例

     算法逻辑

     1. 首先，创建一个空队列 $queue$（用来存放结点）和一个空列表 $visit$（用来存放已访问的结点）
     2. 其次，从 $v_A$ 开始， $v_A$ 进入队列，此时 v i s i t = { ∅ } , q u e u e = { v A } visit=\{\emptyset\},queue=\{v_A\} visit={∅},queue={vA​}
     3. 当 $v_A$ 出队列时 v i s i t = { v A } visit=\{v_A\} visit={vA​}，$v_A$ 的邻接结点 $v_B,v_C,v_D$ 进入队列，此时 q u e u e = { v B , v C , v D } queue=\{v_B,v_C,v_D\} queue={vB​,vC​,vD​}
     4. 接着 $v_B$ 出队列，此时 v i s i t = { v A , v B } visit=\{v_A,v_B\} visit={vA​,vB​}，$v_B$ 的邻接结点中 $v_A,v_E,v_F$ 中未进入队列的 $v_E,v_F$ 进入队列，此时 q u e u e = { v C , v D , v E , v F } queue=\{v_C,v_D,v_E,v_F\} queue={vC​,vD​,vE​,vF​}
     5. 然后 $v_C$ 出队列，此时 v i s i t = { v A , v B , v C } visit=\{v_A,v_B,v_C\} visit={vA​,vB​,vC​}，$v_C$ 的邻接结点中 $v_A,v_D,v_F,v_G$ 中未进入队列的 $v_G$ 进入队列，此时 q u e u e = { v D , v E , v F , v G } queue=\{v_D,v_E,v_F,v_G\} queue={vD​,vE​,vF​,vG​}
     6. 再然后 $v_D$ 出队列，此时 v i s i t = { v A , v B , v C , v D } visit=\{v_A,v_B,v_C,v_D\} visit={vA​,vB​,vC​,vD​}，$v_D$ 的邻接结点中 $v_A,v_C,v_G$ 已经全部进入过队列的故不再入队，此时 q u e u e = { v E , v F , v G } queue=\{v_E,v_F,v_G\} queue={vE​,vF​,vG​}
     7. 最后 $v_E,v_F,v_G$ 结点与 $v_D$ 情况类似，一直出队列直到 q u e u e = { ∅ } , v i s i t = { v A , v B , v C , v D , v E , v F , v G } queue=\{\emptyset\},visit=\{v_A,v_B,v_C,v_D,v_E,v_F,v_G\} queue={∅},visit={vA​,vB​,vC​,vD​,vE​,vF​,vG​}

     算法实现

     graph_nt = {
         'A' : ['B','C','D'],
         'B' : ['A','E','F'],
         'C' : ['A','D','F','G'],
         'D' : ['A','C','G'],
         'E' : ['B'],
         'F' : ['B','C'],
         'G' : ['C','D']
     }
     
     def BFS(start, graph):
         queue = []
         visit = []
         queue.append(start)
         while queue:
             node = queue.pop(0)
             visit.append(node)
             nodes = graph[node]
             for i in nodes:
                 if i not in visit:
                     queue.append(i)
                     visit.append(i)
             print(node, end='\t')
             
     BFS(start='A', graph=graph_nt)
     1
     2
     3
     4
     5
     6
     7
     8
     9
     10
     11
     12
     13
     14
     15
     16
     17
     18
     19
     20
     21
     22
     23
     24
     25

  2. 空间复杂度

     由于 BFS 需要借助一个队列，$n$ 个顶点均需要入队一次，所以最坏情况下 $n$ 个顶点在队列，那么则需要 $O(|V|)$ 的空间复杂度

  3. 时间复杂度

     邻接矩阵，每个顶点入队一次，时间复杂度为 $O(|V|)$，对于每个顶点，搜索它的邻接点，需要遍历一遍矩阵的一行，所以时间复杂度为 $O(|V|)$，所以总的时间复杂度为 $O(|V{|}^2)$

     邻接表，每个顶点入队一次，时间复杂度为 $O(|V|)$，对于每个顶点，搜索它的邻接点，就需要访问这个顶点的所有边，所以时间复杂度为 $O(|E|)$，所以总的时间复杂度为 $O(|V|+|E|)$

图的应用

• 最小生成树（MST）一个连通图的生成树包含图的所有顶点，并且只包含尽可能少的边，如果带权图则选择所有边之和权值最小的生成树

  1. 普利姆（Prlm）

     1. 从图中找第一个起始顶点 $v_0$，作为生成树的第一个顶点，然后从这个顶点到其他顶点的所有边中选一条距离最近（权值最小）的边。然后把这条边的另一个顶点 $v_1$ 和这条边加入到生成树中
     2. 反复执行直到所有所有顶点都加入到生成树中

     

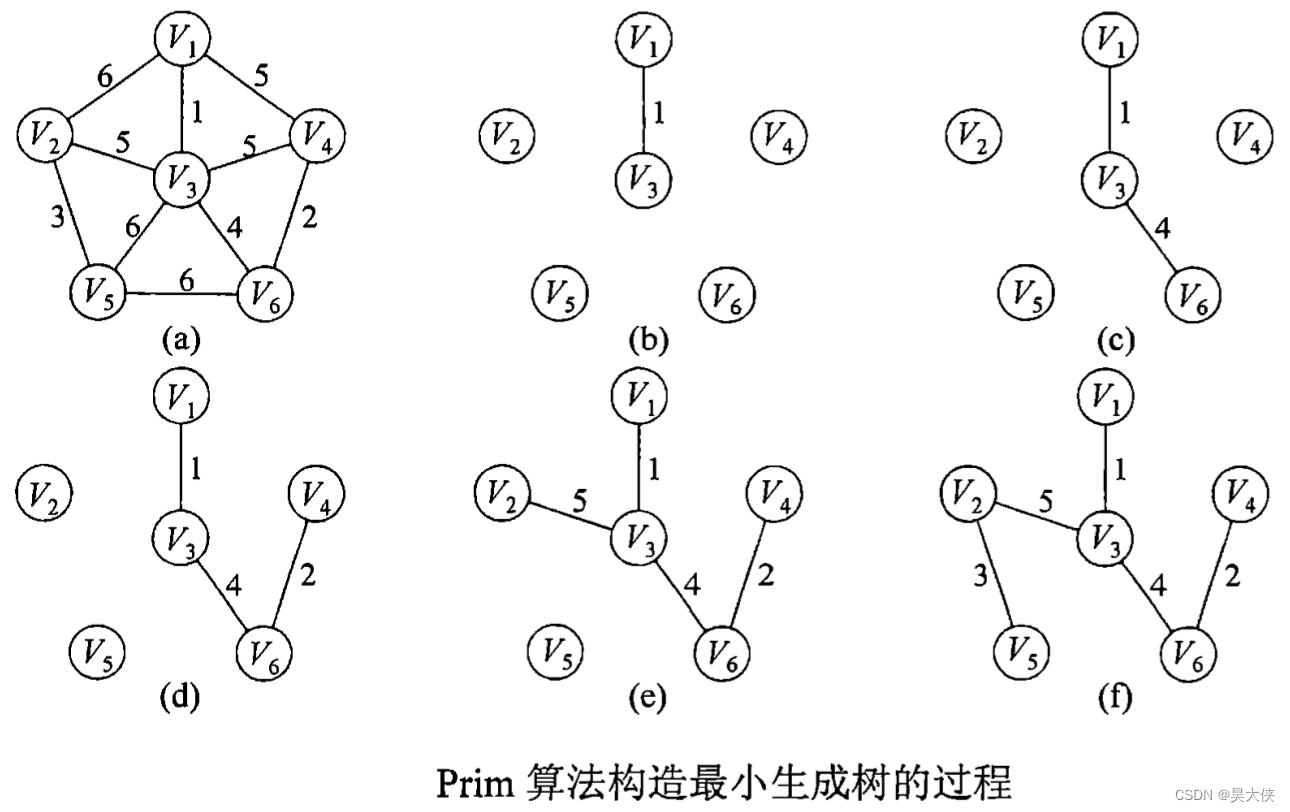
     图 $a$ 的最小生成树普利姆算法构建过程即 $b\to f$，包含双重循环，外层循环次数为 $\mid V\mid -1$，内层并列的循环次数都是 $\mid V\mid$，故普利姆算法时间复杂度为 $O(\mid V{\mid }^2)$，且时间复杂度只和结点数 $\mid V\mid$ 有关，适合稠密图

  2. 克鲁斯卡尔（Kruskal）

     将图中边按照权值从小到大排列存放在堆中，然后从最小的边开始扫描，每次选择最小边的时间复杂度是 $O(log\mid E\mid )$，设置一个边的集合来记录，如果该边并入不构成回路的话，则将该边并入当前生成树，直到所有的边都检测完为止

     

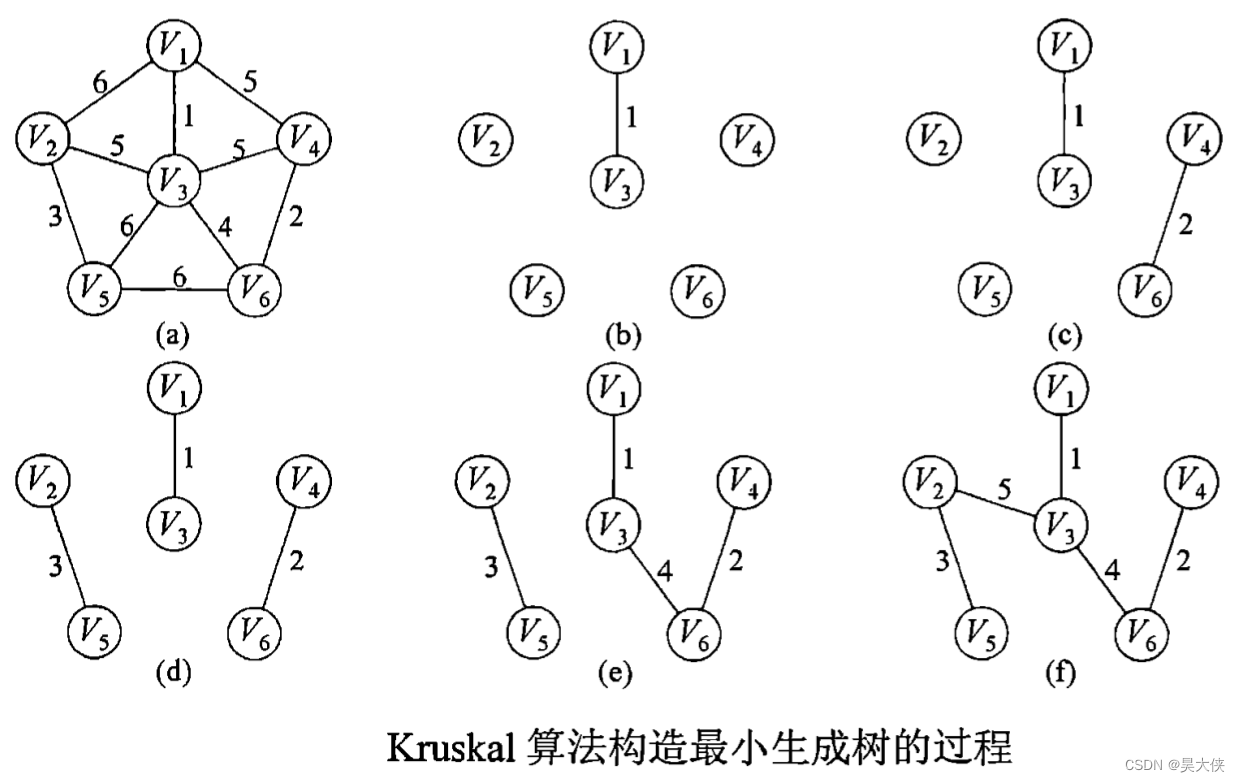
     图 $a$ 的最小生成树克鲁斯卡尔算法构建过程即 $b\to f$，操作分为对边的权值排序部分和一个单重循环，它们是并列关系，由于排序耗费时间大于单重循环，所以克鲁斯卡尔算法的主要时间耗费在排序上，时间复杂度是 $O(\mid E\mid log\mid E\mid )$。排序和图中边的数量有关系，所以适合稀疏图