1.题目

题目链接
题目描述

对于一个 $n$ 个顶点的凸多边形，它的任何三条对角线都不会交于一点。请求出图形中对角线交点的个数。

例如，$6$ 边形：

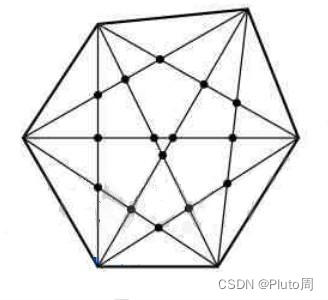
输入格式

输入只有一行一个整数 $n$，代表边数。

输出格式

输出一行一个整数代表答案。

样例 #1
样例输入 #1

3
1

样例输出 #1

0
1

样例 #2
样例输入 #2

6
1

样例输出 #2

15
1

提示
数据规模与约定

• 对于 $50\%$ 的数据，保证 $3\le n\le 100$。
• 对于 $100\%$ 的数据，保证 $3\le n\le 10^5$。

2.分析

找规律
首先，多边形内对角线的交点不可能是三条及以上对角线相交而成
则一个交点是由两条对角线相交而成，而两条对角线对应四个顶点

所以对应关系为：
一个交点< == > 两条对角线 < == >四个顶点

问题转换为：从n个顶点中选出4个顶点的选法，即C 4 N

3.代码

#include <iostream>
using namespace std; 
typedef unsigned long long ull;
int main()
{
	ull n;
	cin >> n;
	if (n <= 3)
		cout << 0;
	else
		cout << n * (n - 1) / 2 * (n - 2) / 3 * (n - 3) / 4;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13

4.总结

坑点

1.数据规模 会爆long long ,选用unsigned long long
2.写法分析

n * (n - 1) / 2 * (n - 2) / 3 * (n - 3) / 4;
1

tips：连续的m个数中，必定有是m的倍数的数
n ( n-1) 中必定有一个是2的倍数
n (n-1) (n-2) 中必定有一个是3的倍数
n (n-1) (n-2) (n-3) 中必定有一个是4的倍数
则上述式子，必定可整除

5.更新日志

2022.6.22 整理上传

欢迎交流讨论、指正~
不正确、不理解之处欢迎评论留言~