一、 图的基本概念

1.1 基本概念

1.1.1 图的 定义

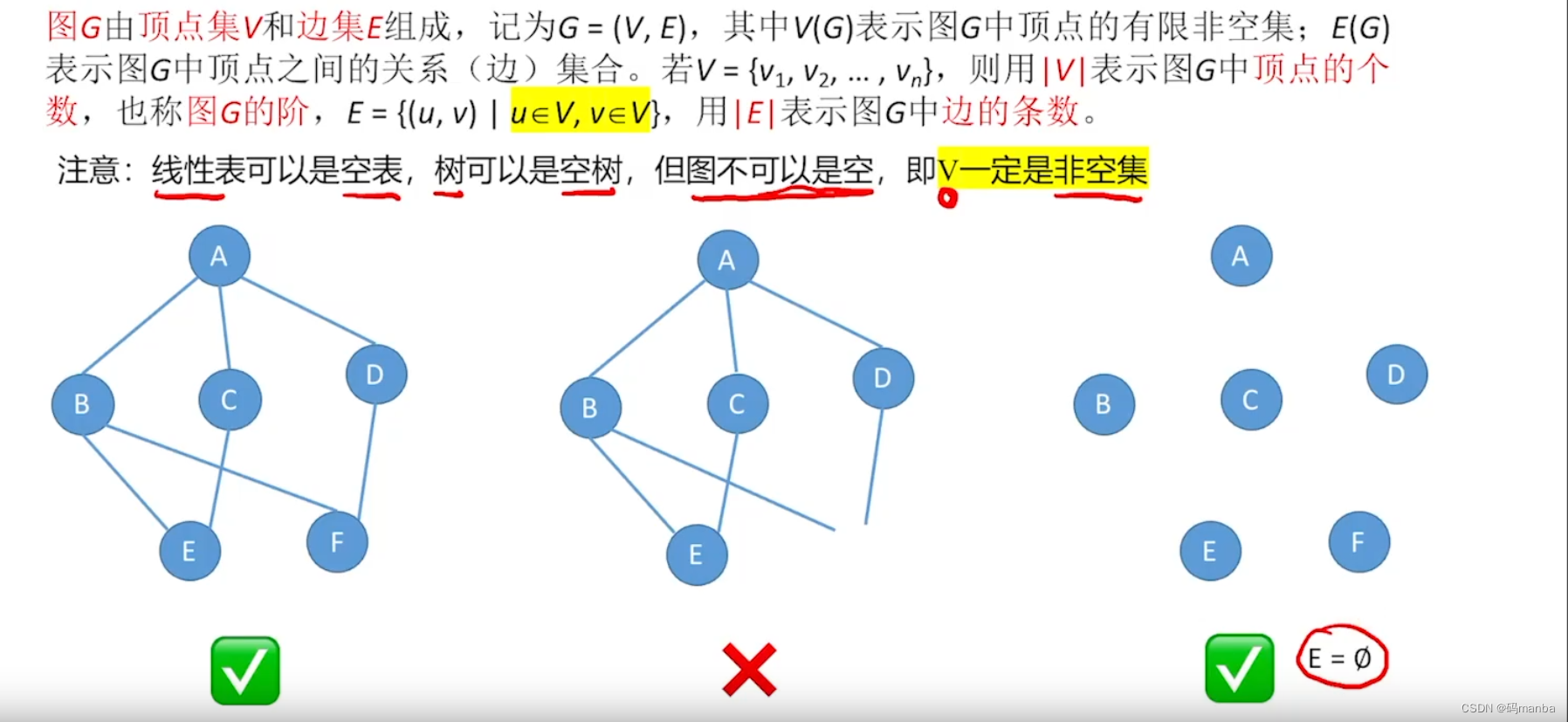
在 以后 设计 交友类软件的时候。
好友关系通过无向图实现。
关注关系通过有向图实现。

1.1.2 各种术语概念

有向图、无向图

简单图、多重图

顶点的度（入度、出度）

路径、路径长度、回路、简单回路、 简单路径、距离、 连通（无向图）、 强连通（有向图）

连通图、强连通图

子图、生成子图

连通分量、强连通分量

生成树、生成森林

边的 权、 带权图、 带权路径长度

完全有向图、完全无向图

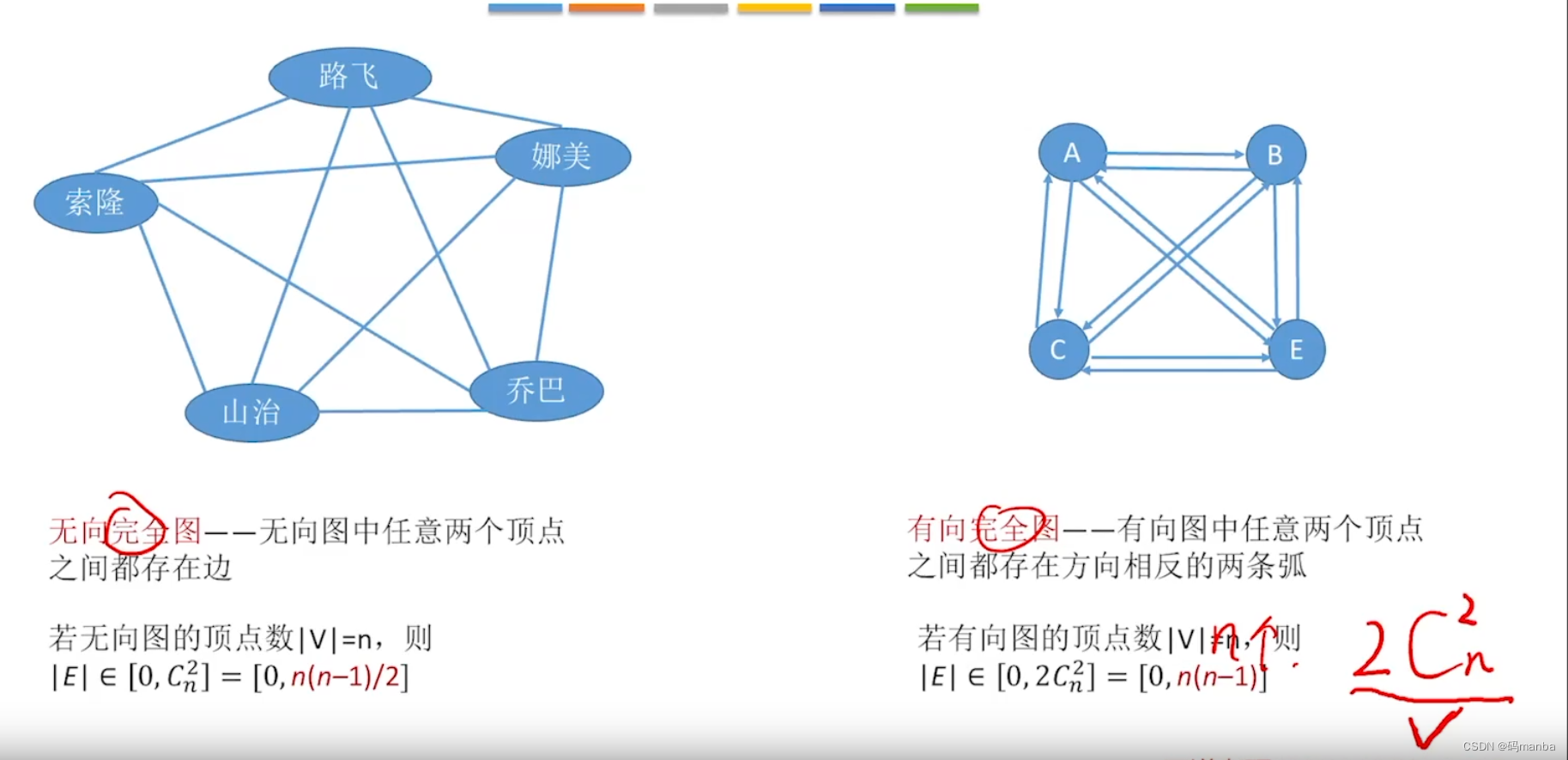
稀疏图、稠密图

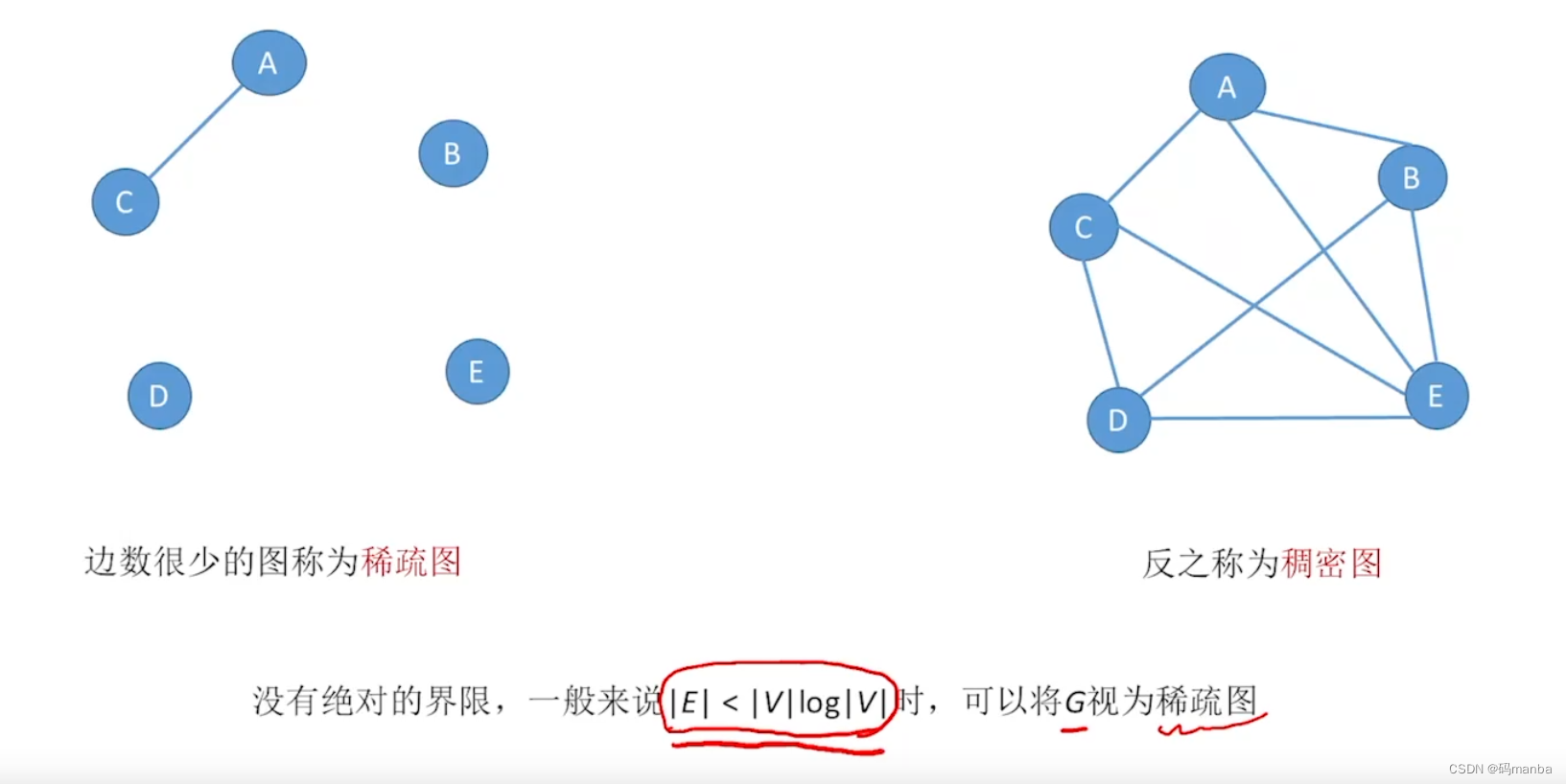
树(无向图)、有向树（有向图）

• 树是 连通图
• 但 有向树 并不是 强连通图

小总结

二、 图的存储及基本操作

2.1 各种图的存储结构

1. 邻接矩阵法（思想与代码实现）

⭐ 介绍邻接绝阵

• 通过 一个 一维数组VEX 存储 顶点信息 （顶点表）；
• 通过 一个二维bool数组 Edge 存储 两顶点对应是否有连接关系（邻接矩阵）；
• 注意： 无向图的邻接矩阵是对称矩阵，可通压缩矩阵算法实现存储；

⭐ 通过邻接矩阵计算 顶点的度（有向/无向）

⭐ 带权邻接矩阵

• 一般无穷表示两个顶点间无路径；
• 0表示 自己到自己；

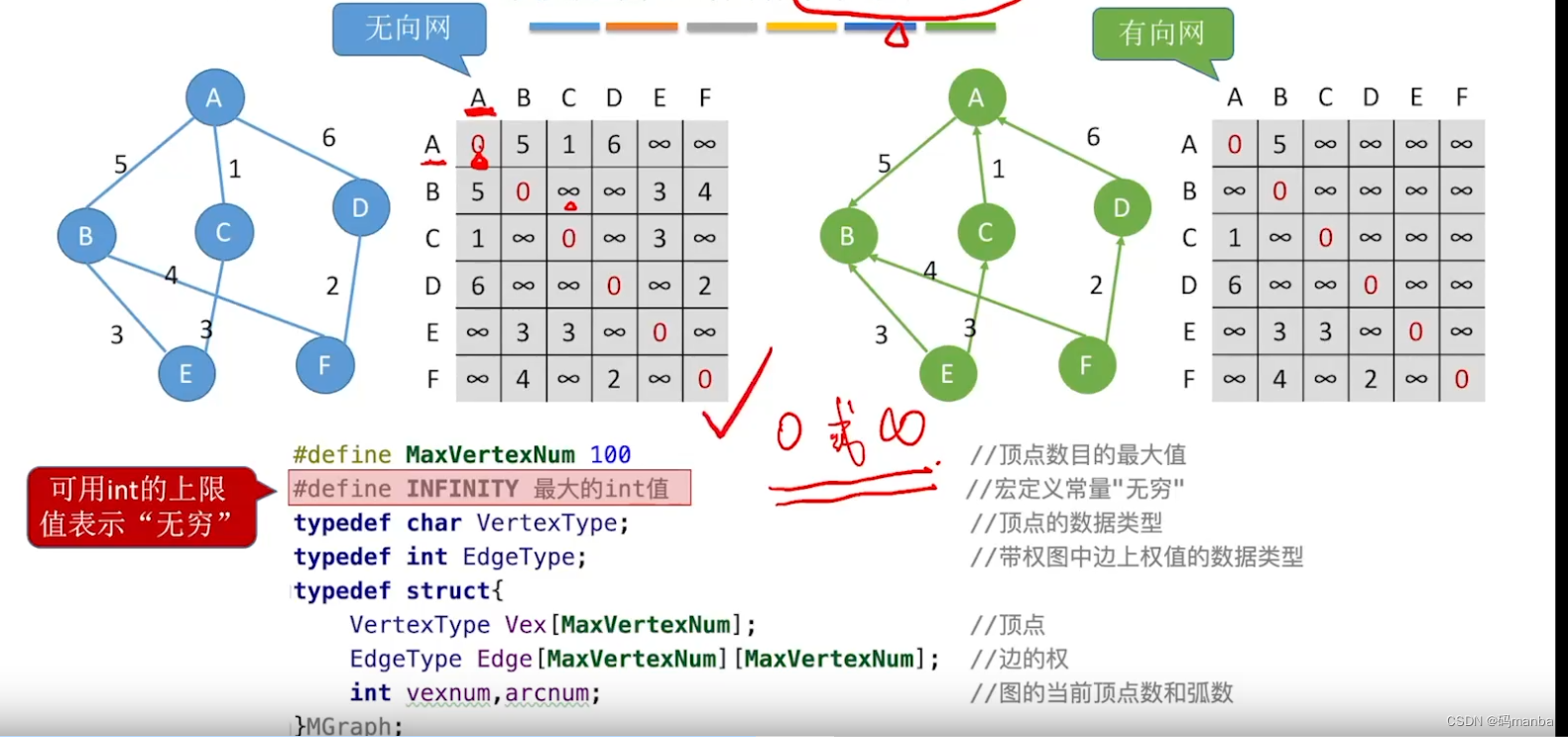
⭐ 邻接矩阵 空间复杂度

• 可通过 压缩矩阵存储 来 存储 无向图的 邻接 矩阵

⭐ 邻接 矩阵的 性质

• 这个用来求，邻接矩阵的n次幂。 指 两个结点 直接 存在路径 长度为 n 的 个数；

2. 邻接表法

• 无向图的 邻接 表示法， 类似于 树的 孩子表示法；
• 通过 一个 顶点数组保存各个顶点， 每个顶点结点有自己的信息域和 第一个边域（指向一个邻接的点）；
• 通过 边结点，连接每个结点的所有边， 每个边结点都有 指向哪个结点信息域，与 下一条边结点的指针域。

⭐ 邻接表 之 有向图 和 无向图

• 当 求无向图的 每个结点的度的时候：
  1. 只需要 从结点域开始向后遍历即可；
• 当求 有向图的 每个 结点的 度的时候：
  1. 求出度，就是从顶点开始向后遍历链表；
  2. 求入度，就异常的困难！需要遍历每个结点边，对每个结点进行遍历判断，极非时间；

⭐ 对比 邻接表 与 邻接 矩阵

⭐ 邻接表的特点：

3. 十字链表法

⭐ ： 十字链表 只针对 与 有向图；

• 对于顶点结点：
  1. data： 存储顶点信息；
  2. firstin： 以 该顶点作为 弧头 的 第一条弧； 就是箭头所在端；
  3. firstout： 以 该顶点作为 弧尾 的 第一条弧； 就是没有箭头所在一端；
• 对于弧结点（就是边）：
  1. tailvex： 指的弧尾编号；
  2. headvex： 指的弧头编号；
  3. tlink： 弧尾相同的 下一条弧；
  4. hlink： 弧头相同的 下一条弧；
  5. info： 弧的有关信息

• 将 图以具体图的形式转换成 十字链表, 具体思想;

1. 找到一个点，该点所指向的 第一点 的 弧 用 firstout指向； 指向的弧结点 通过 tlink连接 弧尾相同的弧，也就是 该结点的剩余的所有弧；
2. 找个的这个点， 被别的结点所指向 ， 指向的弧 用该结点 的 firstin 指向。 所指向的弧结点的 同样串联相同的弧尾弧头指向；

⭐ 十字链表法 计算 出边 与 入边；

• 计算某结点的入度；
  1. 在点结点 通过 firstin 指针域 指向 第一个 弧（该弧为该结点入度的弧）开始 遍历 弧结点的 headvex（指向有共同入边的其他弧结点）
• 计算某结点的出度：
  1. 从点结点的 firstout 指针域 指向的 第一个 弧（该弧为该结点出度的弧）开始 遍历 弧结点的 tailvex（指向 有共同出边的其他弧结点）

邻接多重表

属于 无向图

• 顶点结点：
  1. data： 存储该顶点的信息；
  2. firstedge： 指向该顶点 连接的 第一条边 的 弧结点；
• 边结点：
  1. i、j： 指的是 该边连接的 两个顶点编号
  2. ilink： 指的是 i 顶点，所连接的另一条边的 弧结点；
  3. jlink： 指的是 j 顶点，所连接的另一条边的 弧结点；

⭐ 邻接多重表的 分析

四大图的 存储 方式 总结

2.2 基于 邻接矩阵和邻接表的 图的基本操作

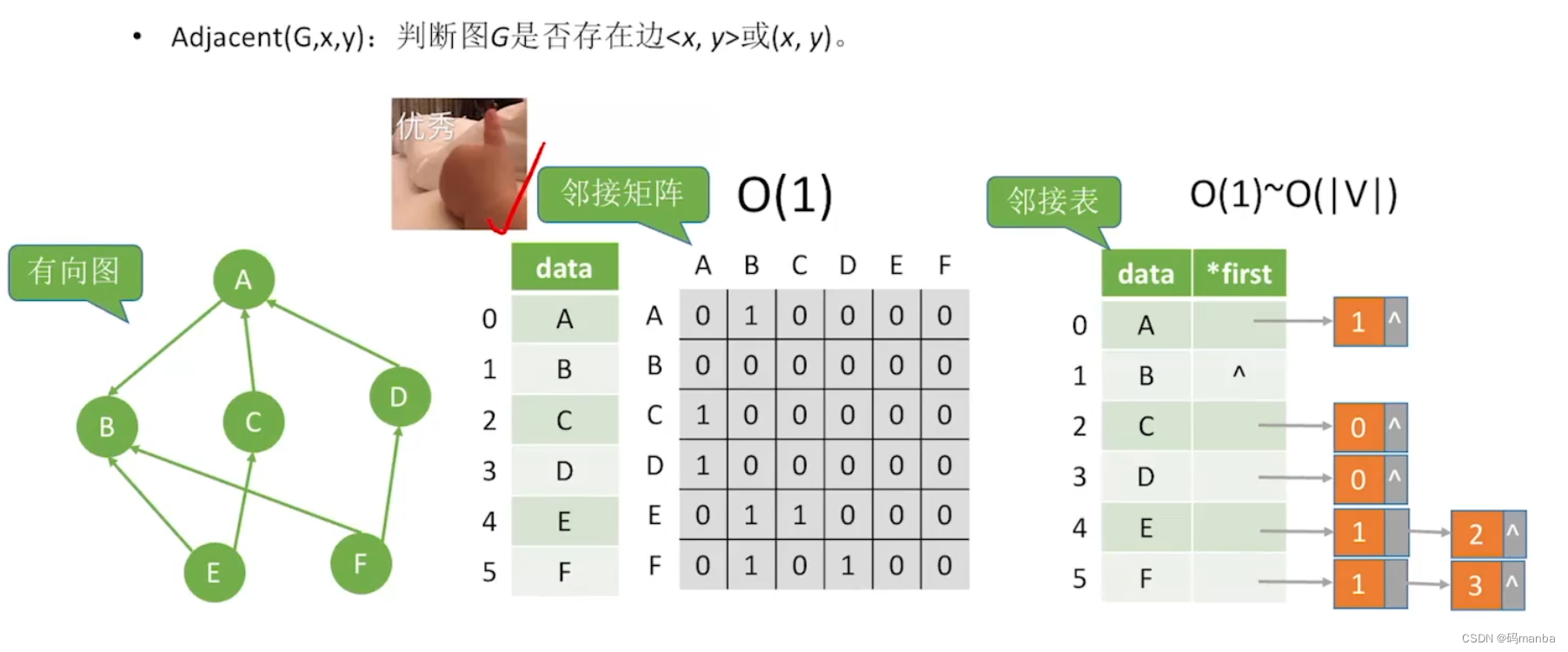
2.2.1 判断 两点之间 是否存在边

⭐ 无向图

⭐ 有向图

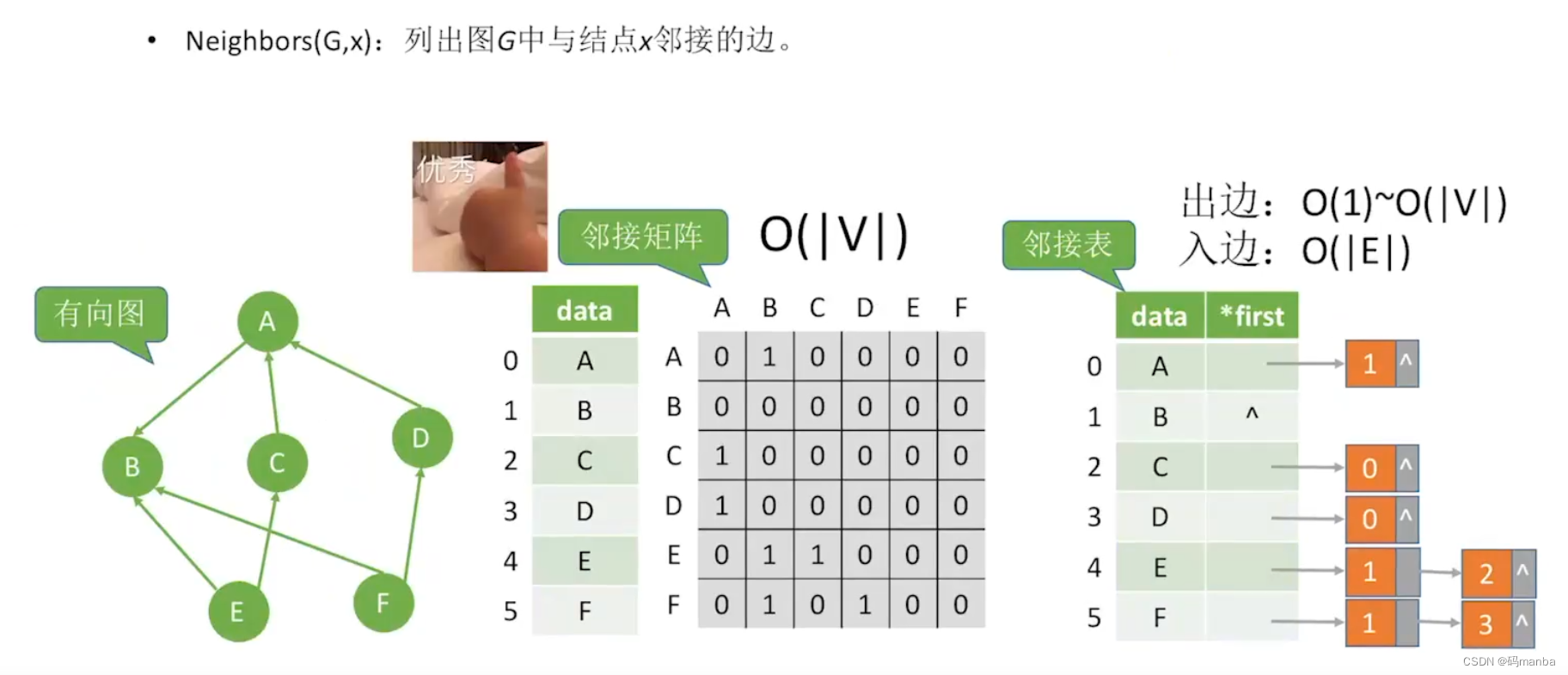
2.2.2 找出 图中 与 某 结点 连接的 所有边

⭐ 无向图

⭐ 有向图

2.2.3 在 图 中 插入 新结点

⭐ 有向图 无向图 一样

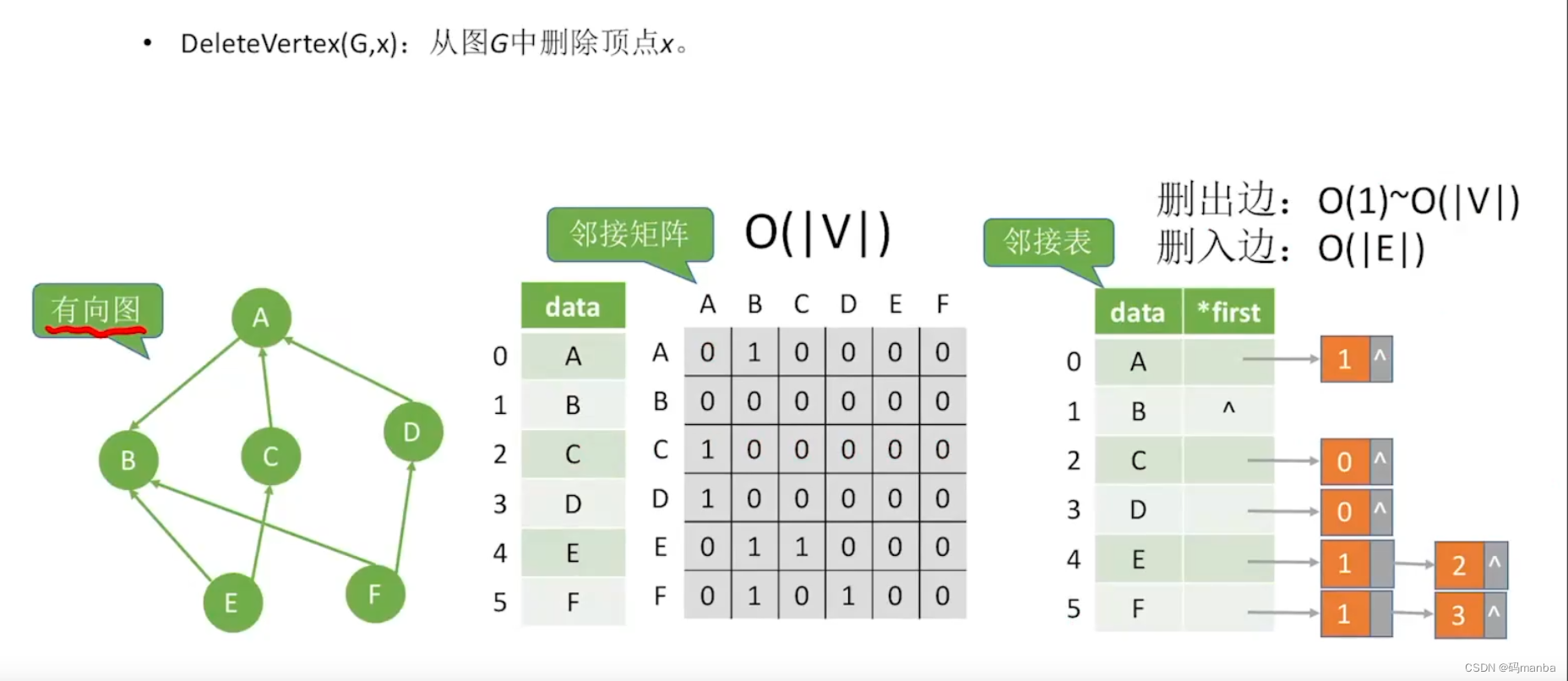
2.2.4 在 图 中 删除 一个 结点

⭐ 无向图

⭐ 有向图

2.2.5 在 图中 增加 一条边

⭐ 有向图 无向图 类似

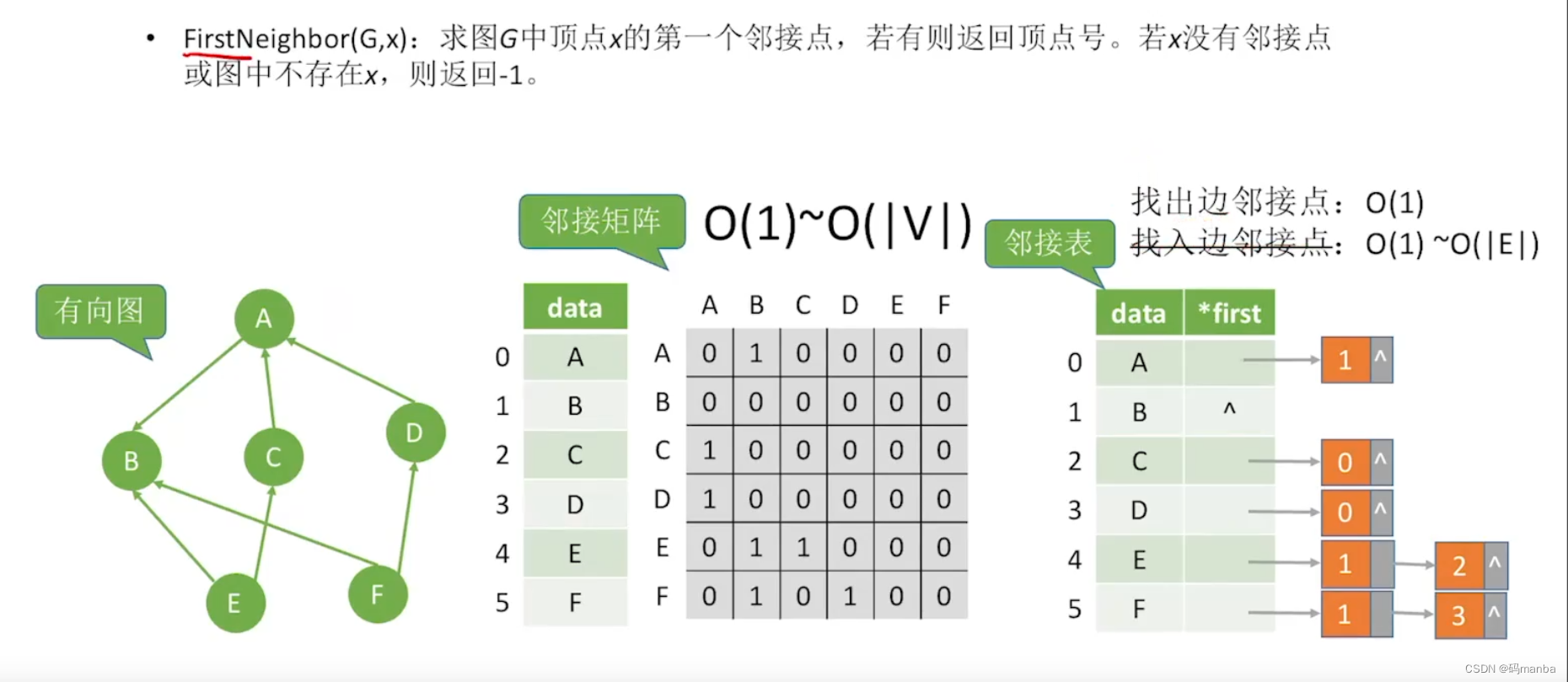
2.2.6 寻找 图 的 某节点 的 第一个 邻接点

⭐ 无向图

⭐ 有向图

• 对于邻接 矩阵：
  1. 找n(n下标)出边就是 遍历 第n行
  2. 找n的入边就是 遍历 第n列

2.2.7 寻找图 的 某个 结点 的 第二个 邻接点

⭐ 无向图

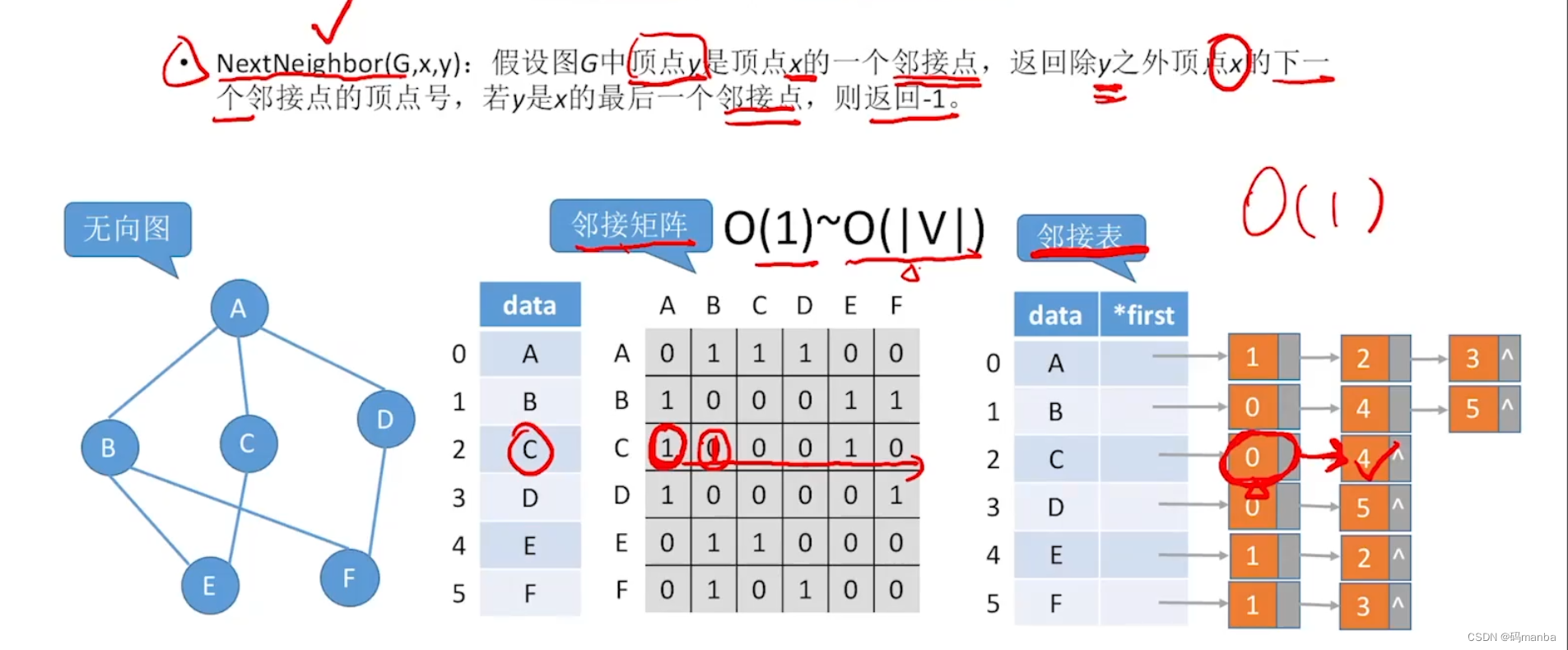
2.2.8 设置/获取 某条边 的 权值

• 这个算法 核心就是 找到 要操作的边， 因此 时间复杂度就是 找边的 时间复杂度

2.2.9 基于 邻接矩阵和邻接表的 图的基本操作 小总结

三、图的遍历

3.1 图的广度优先遍历

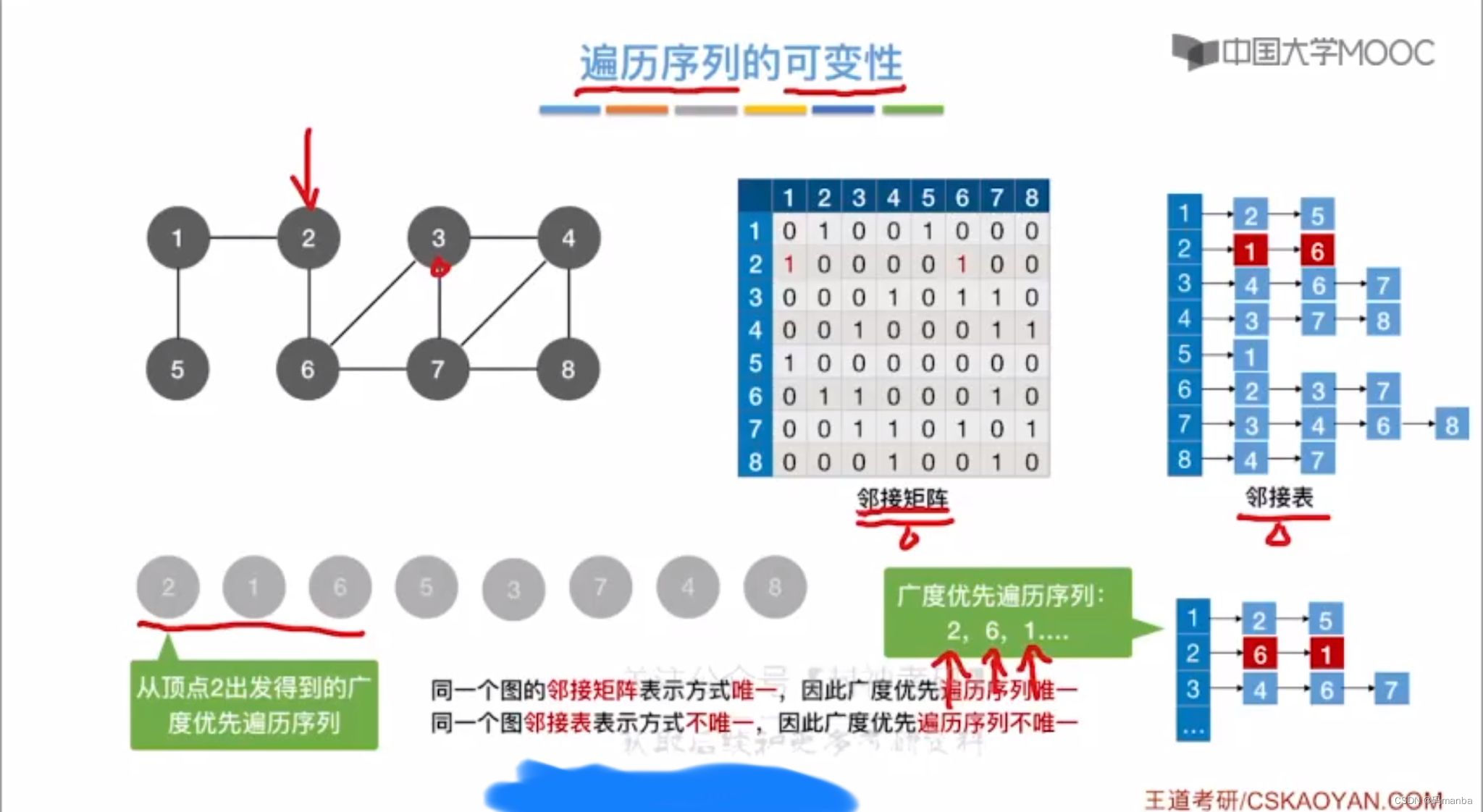
图的存储方式

• 广度优先遍历，，邻接矩阵的存储图遍历是唯一的，但是如果存储方式是邻接表的话，遍历的顺序就不唯一

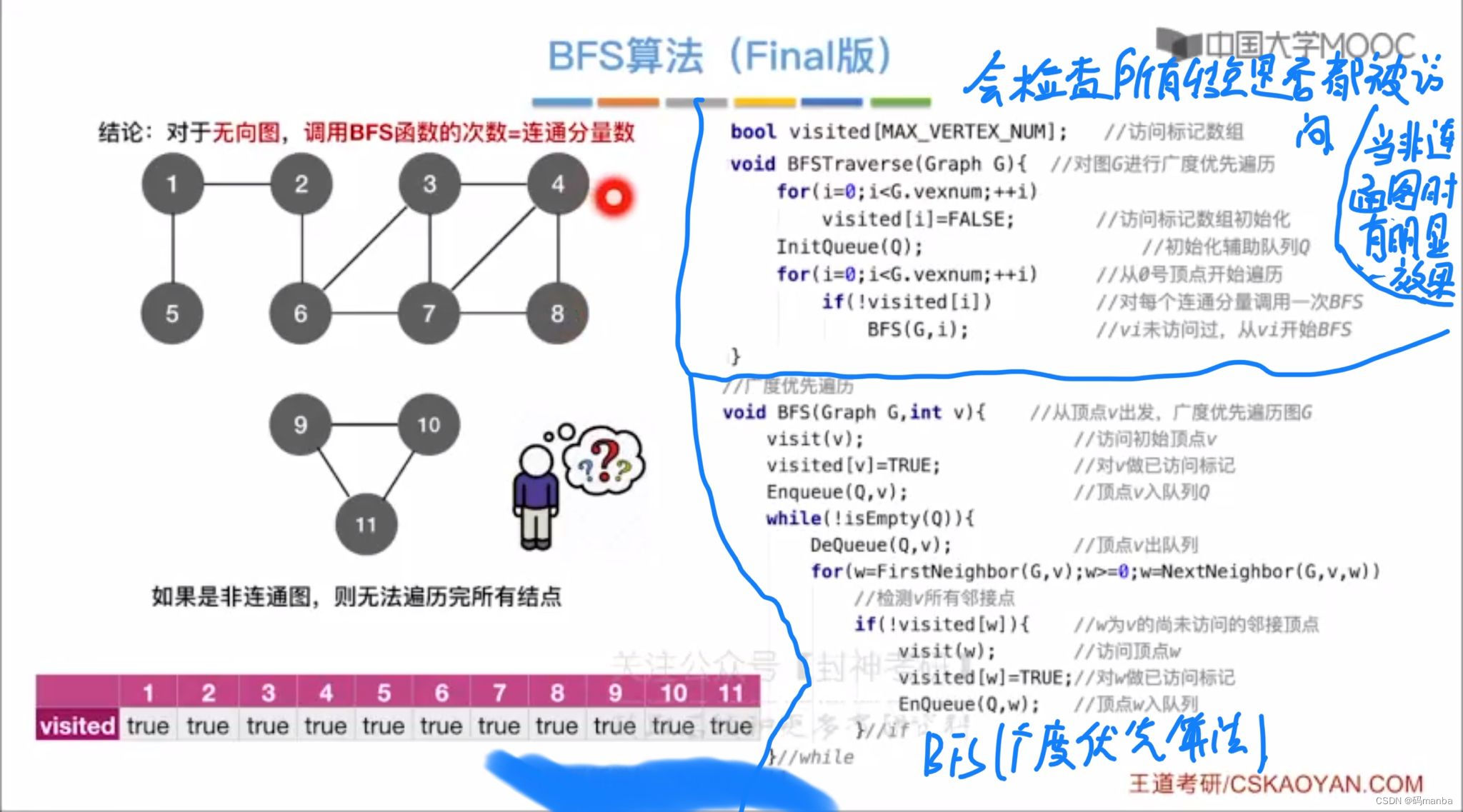
广度优先遍历算法代码

• 对于无向图，调用bfs函数的次数等于连通分量的个数，因为bfs一次会遍历一个连通分量
• 注意，当有向图进行广度优先遍历的时候。 从不同的结点出发遍历dfs的次数可能不一样

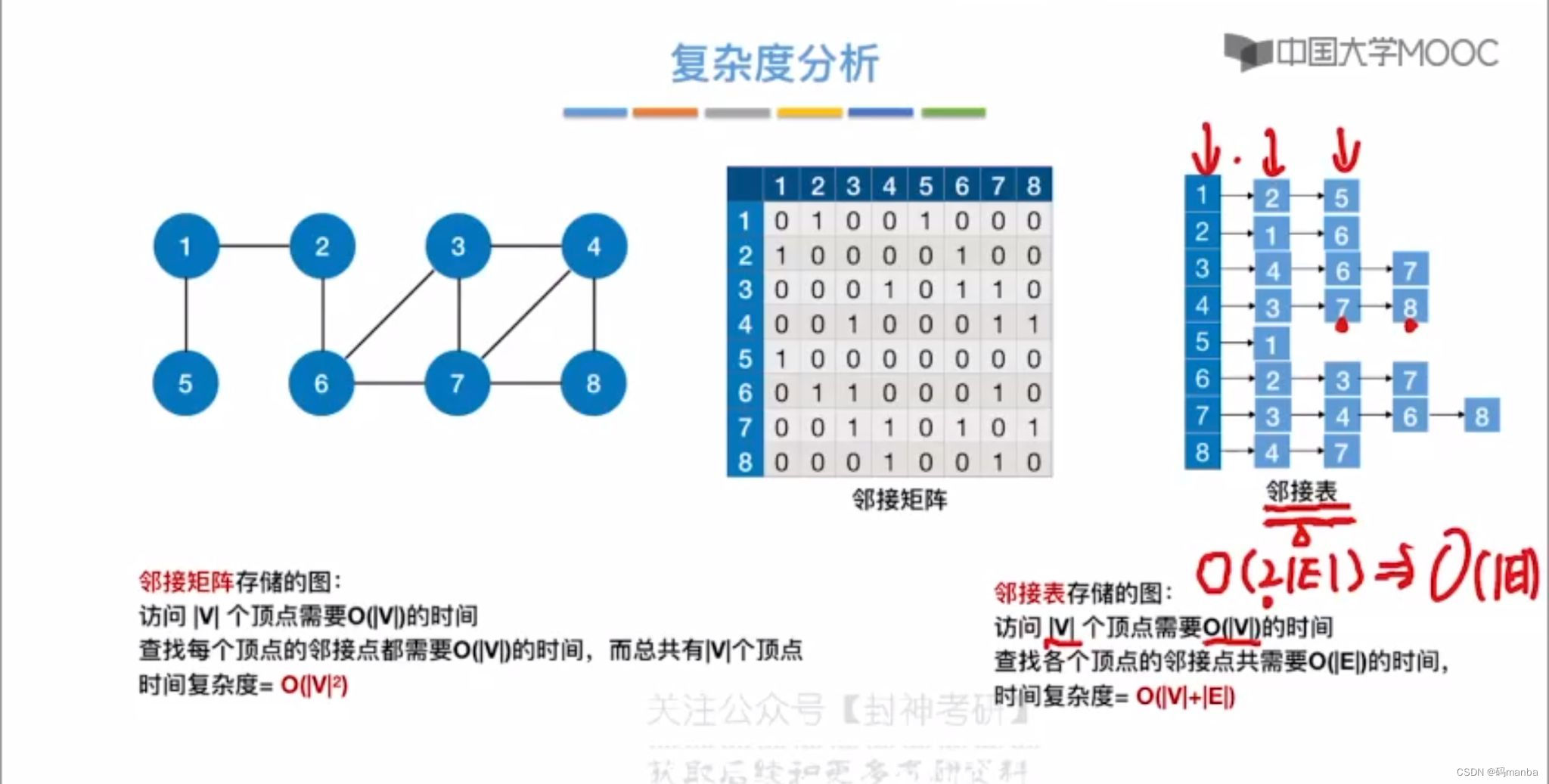
广度优先遍历算法的时间复杂度

• 分析时间复杂度就是找多少顶点，找对应多少边，不要陷入bfs中

广度优先生成树

• （广度优先生成树）对图进行第一次广度优先遍历的时候，每个结点第一次被访问的路径被记录下来，这样一颗连通的图就会产生一颗生成树

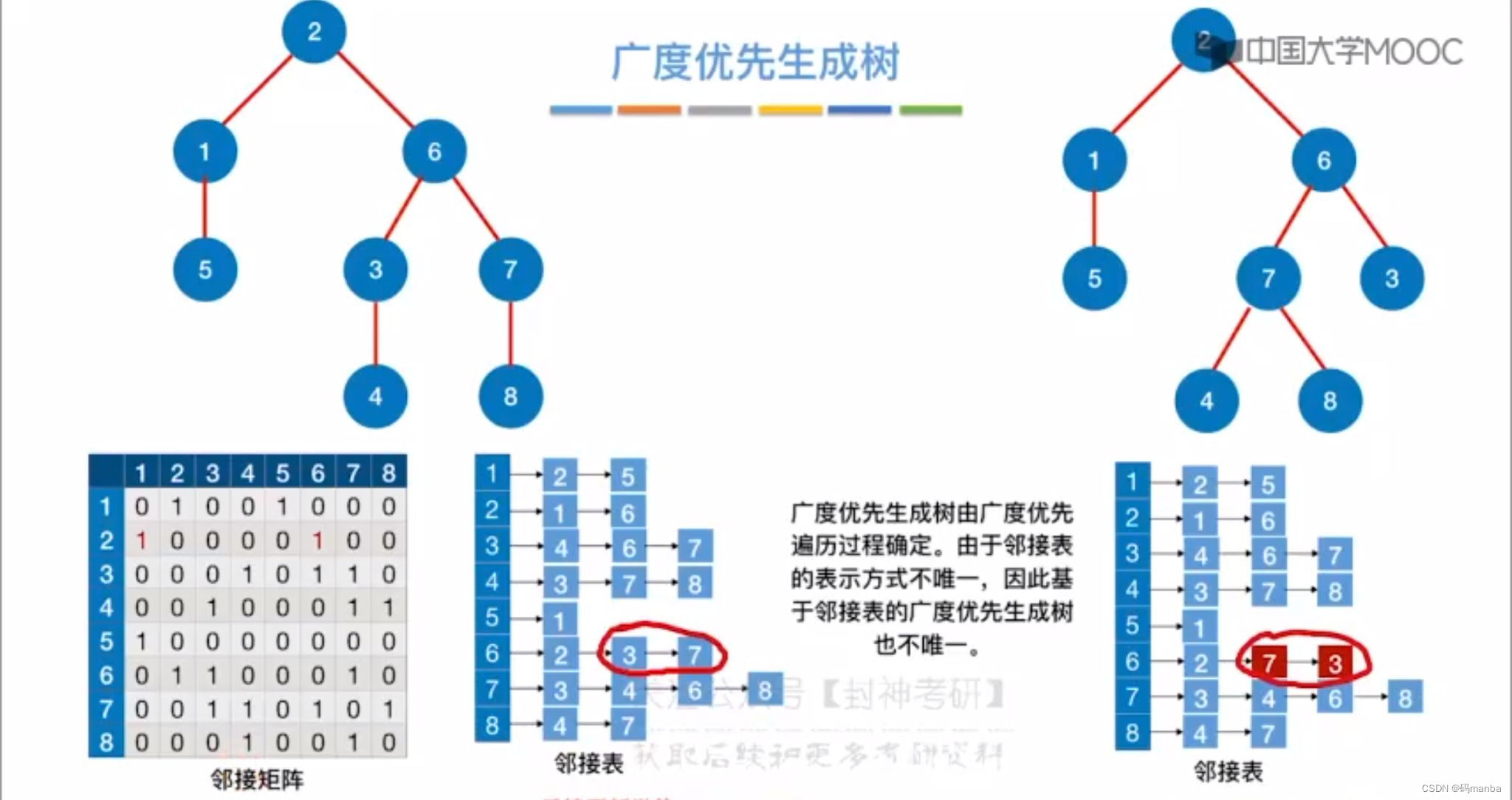
⭐ 当存储结构是邻接表的时候，因为邻接表的存储可能不一，则广度优先遍历可能不一样，所以广度优先生成树的形状也可能不一样
所以对于非连通图，每个连通分量都可以生成一颗广度优先生成树。这个非连通图就可以生成广度优先森林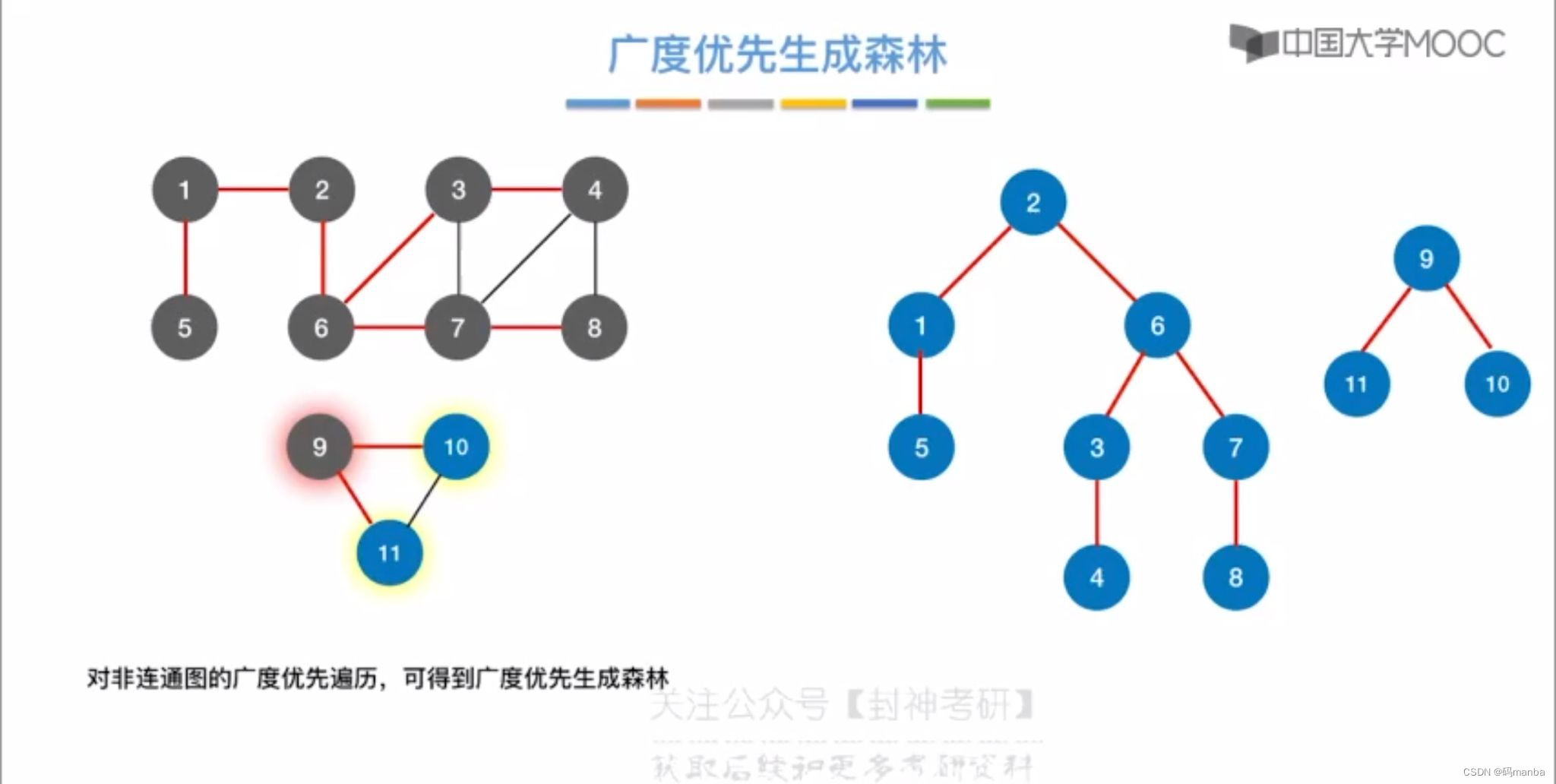

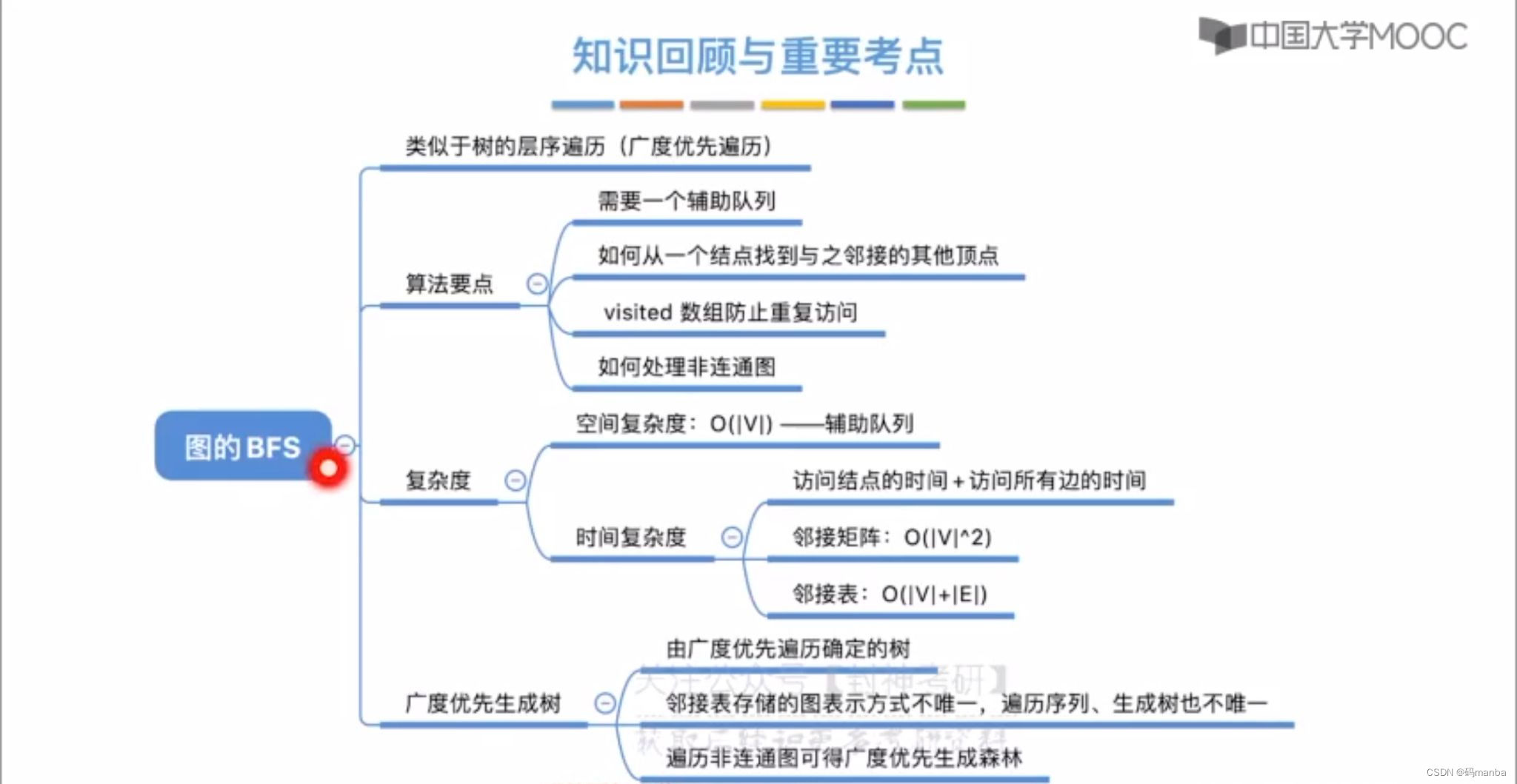
广度优先遍历知识整理

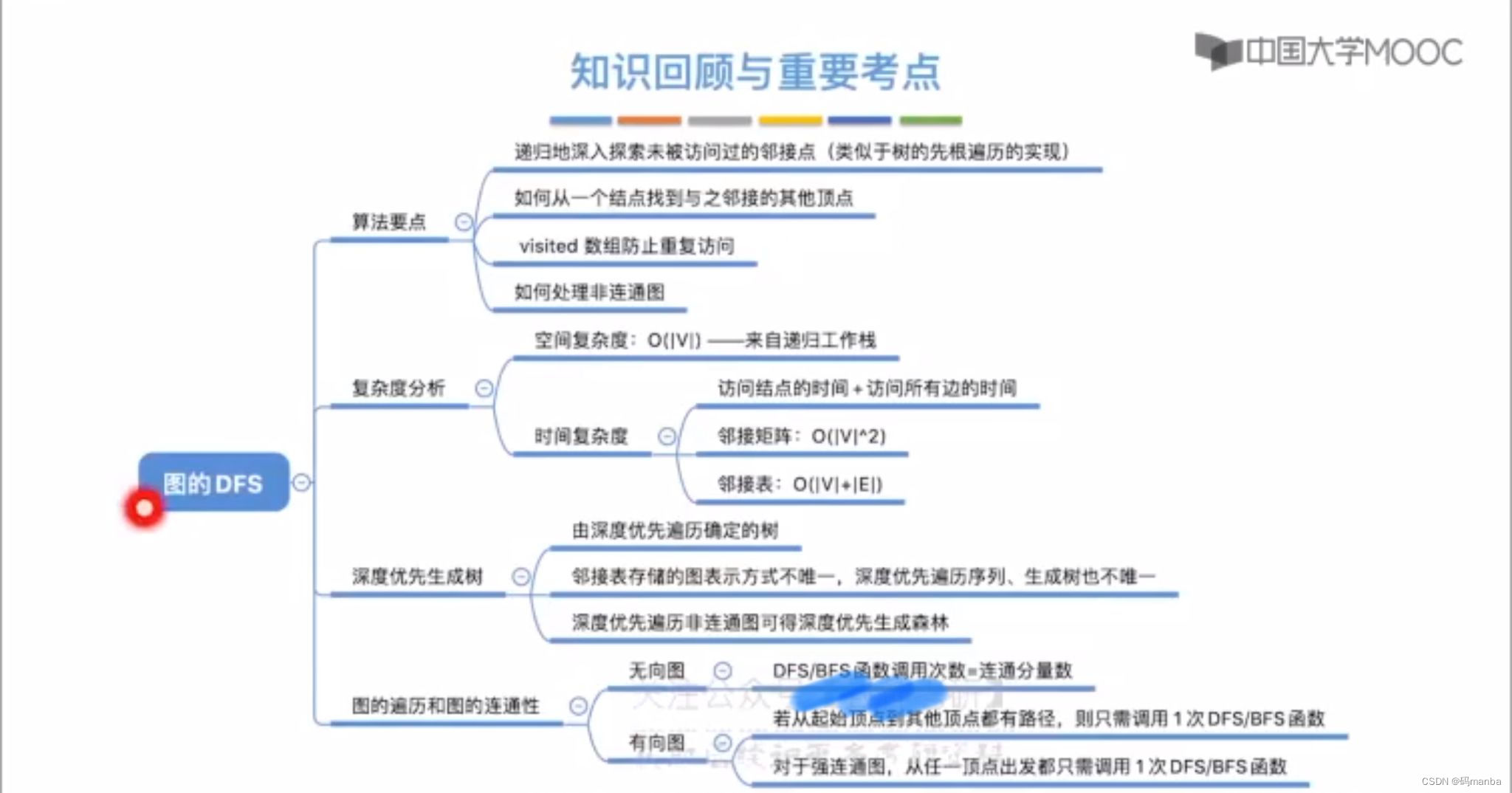
3.2 深度优先遍历

图的深度优先遍历类似于树的先根遍历

深度优先算法代码

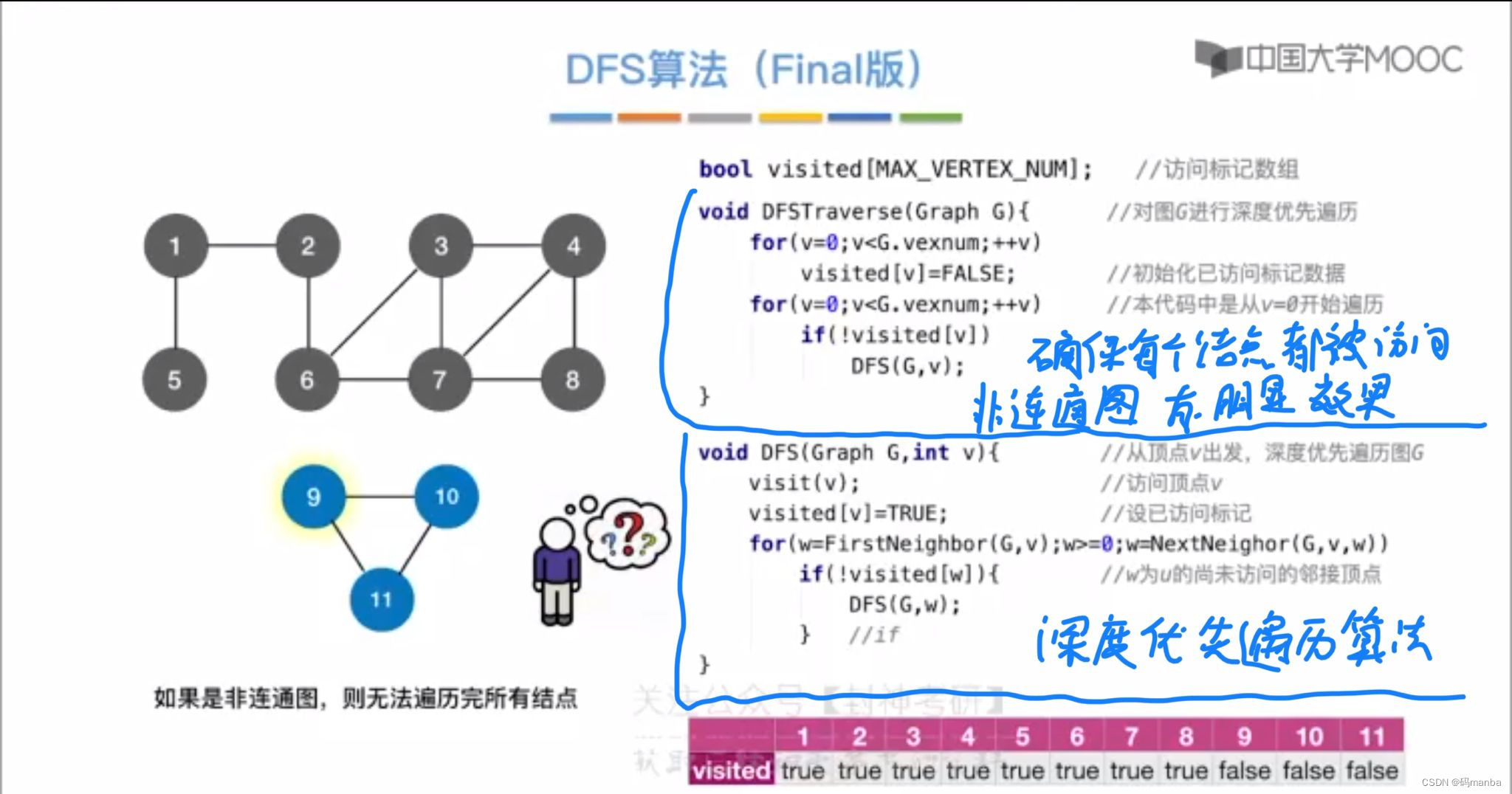
深度优先算法的空间复杂度

⭐ 注意这个空间复杂度关键是递归所占有的空间。而广度优先遍历的算法中空间复杂度是和辅助队列有关

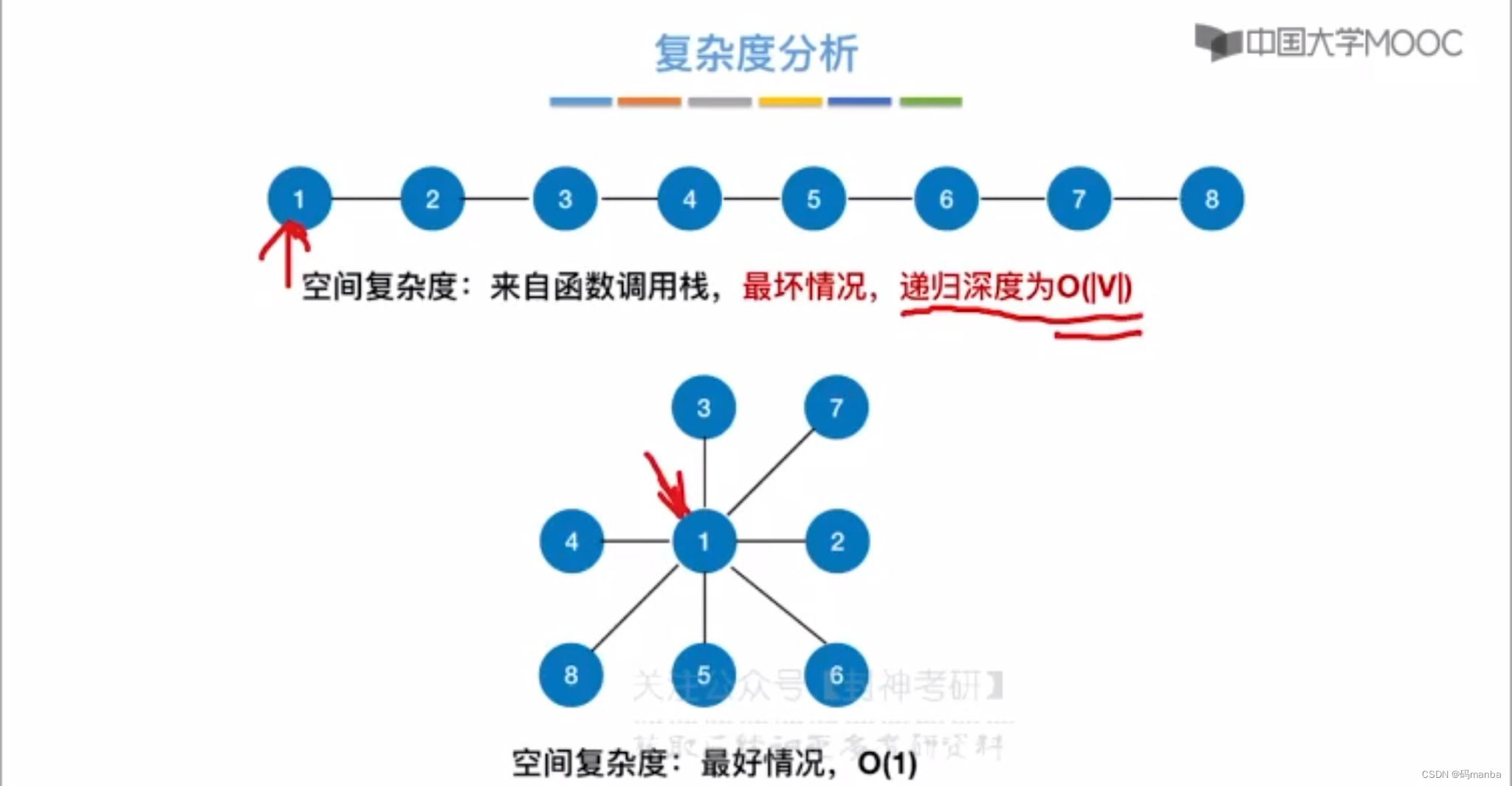
深度优先遍历的时间复杂度

• 与广度优先遍历一样，都是取决于存储方式

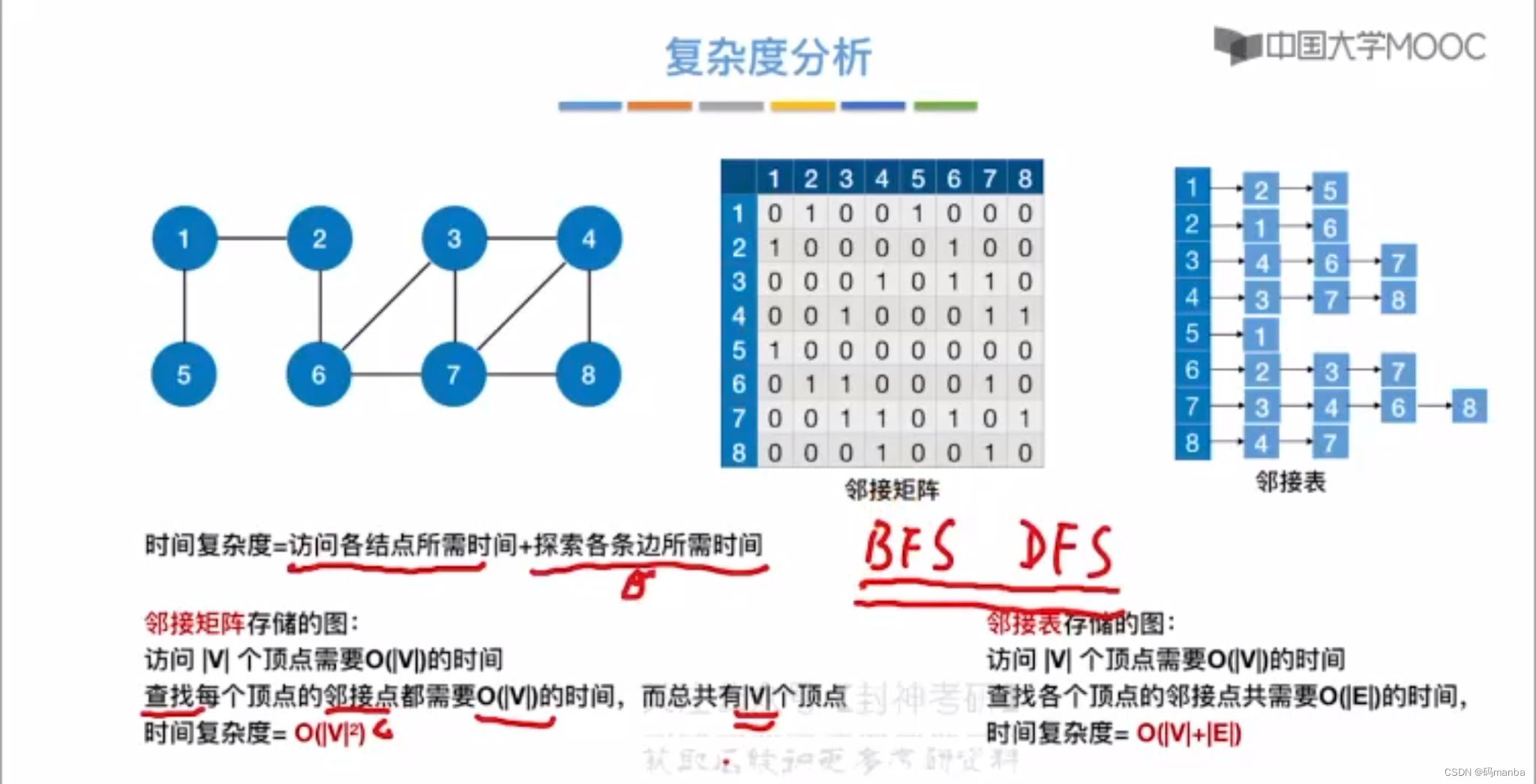
• 同样基于邻接表的存储结构，图的深度优先遍历可能会不同

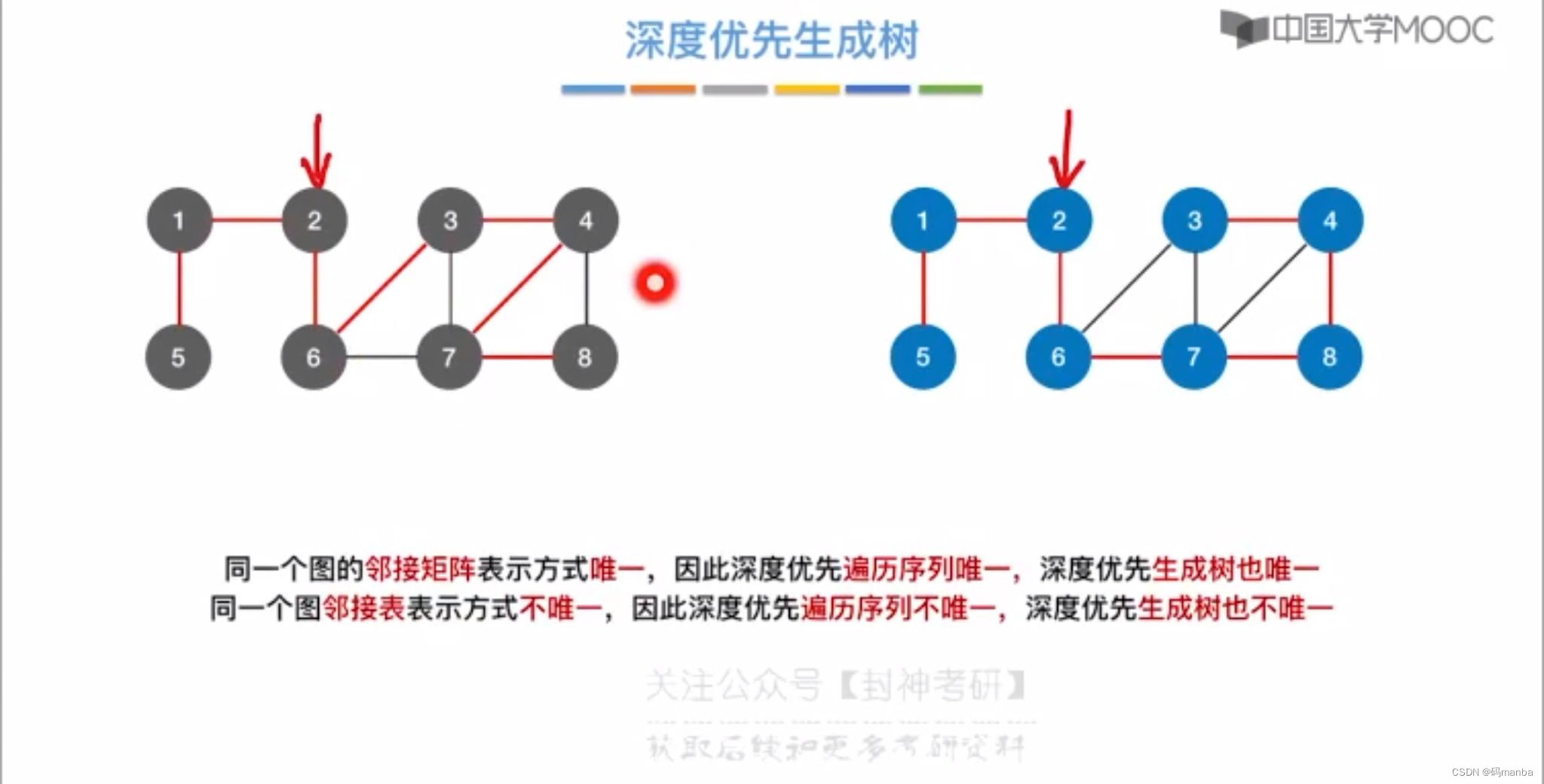
深度优先生成树

• 深度优先生成树，就是图进行深度优先遍历的时候，每个结点最先被访问的路径
• 同样对于非连通图，也就有了深度优先生成森林

• 其实不管是深度优先和广度优先，都是对每个结点探索有没有连接路径的过程。广度是先探索一个结点所有的连接点，而深度则是从一个结点开始，依次往下遍历的过程

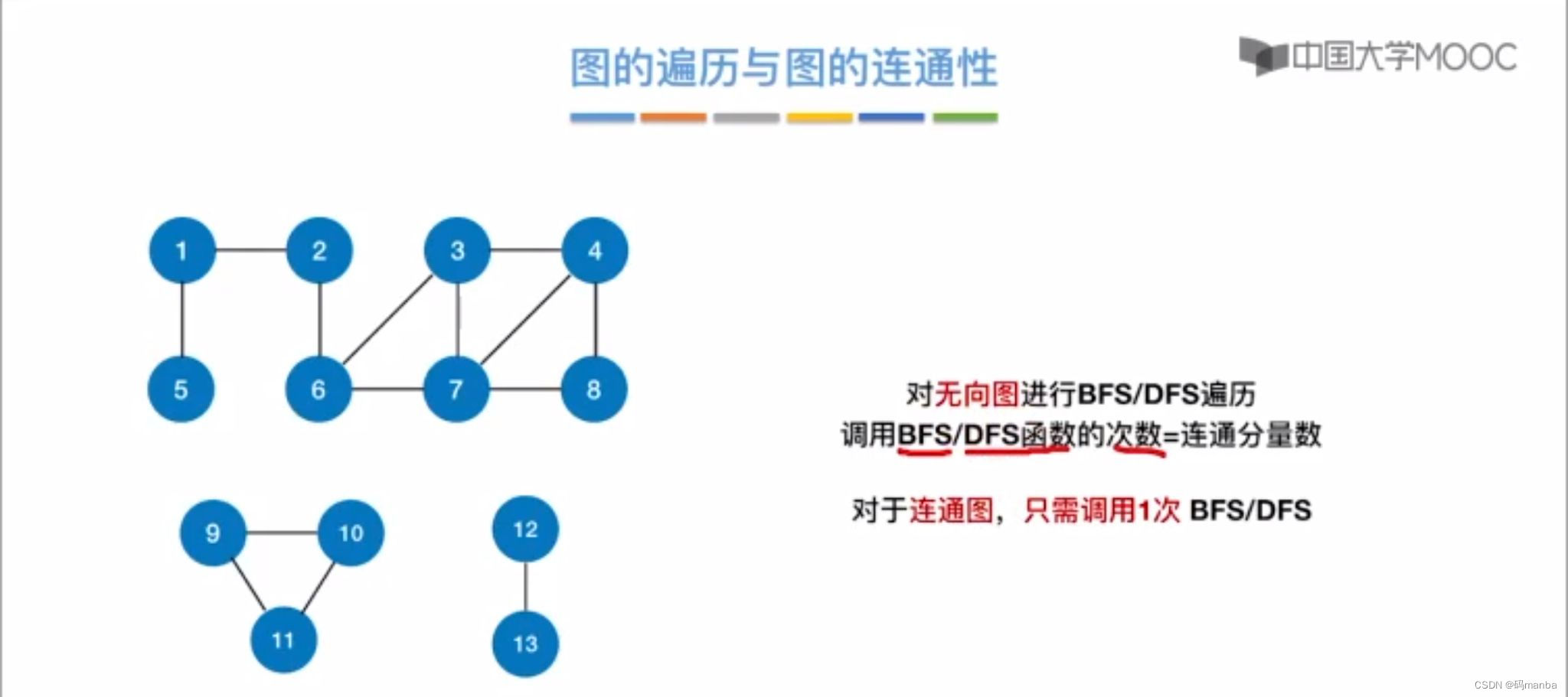
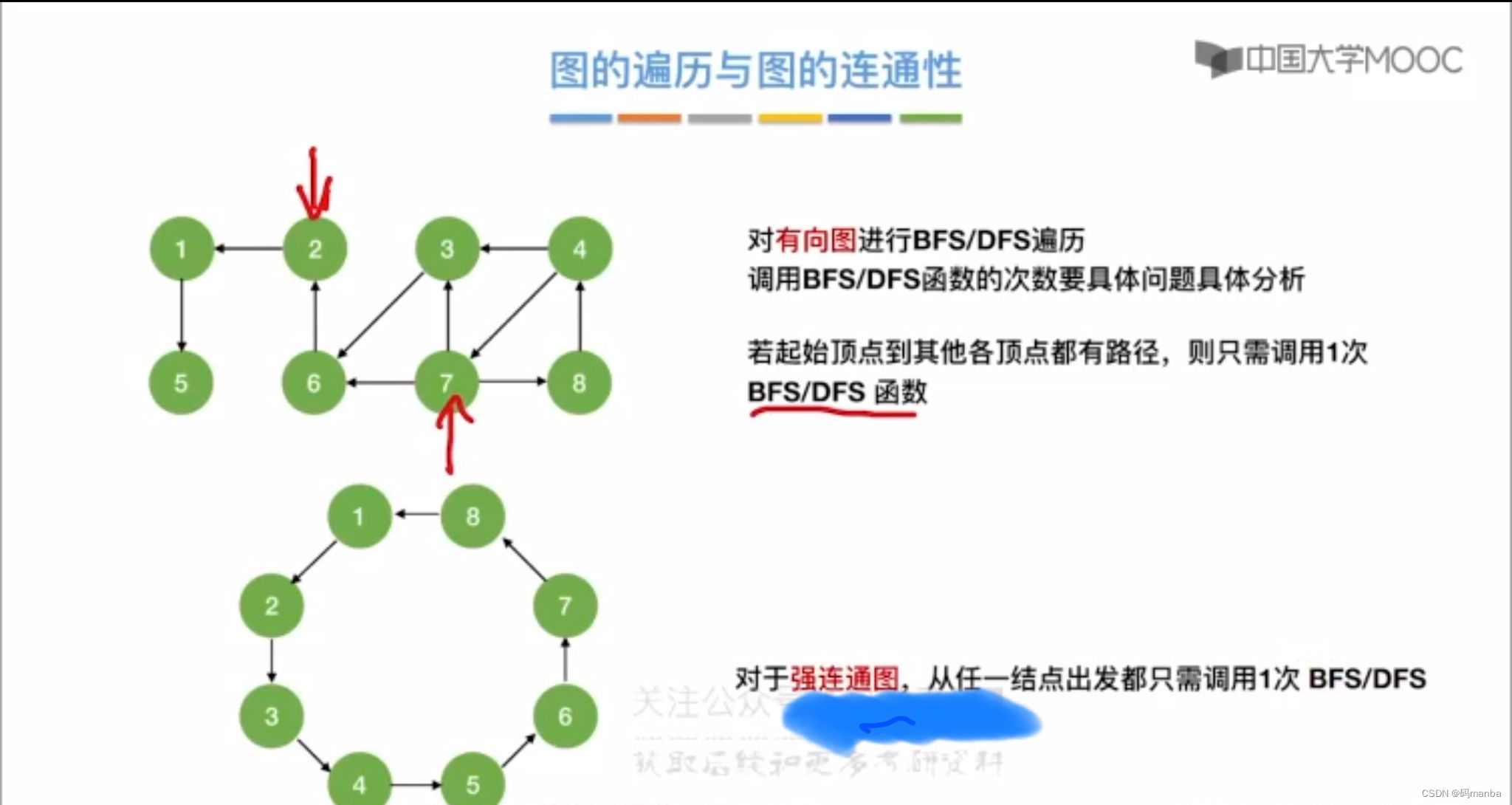
3.3 图的遍历与图的连通性关系

1. 无向图

• 连通分量决定了dfs或者bfs的调用次数(对于无向图而言
  )
  

2. 有向图

• 有向图连通性，与遍历的关系

知识框架

四、 图的应用

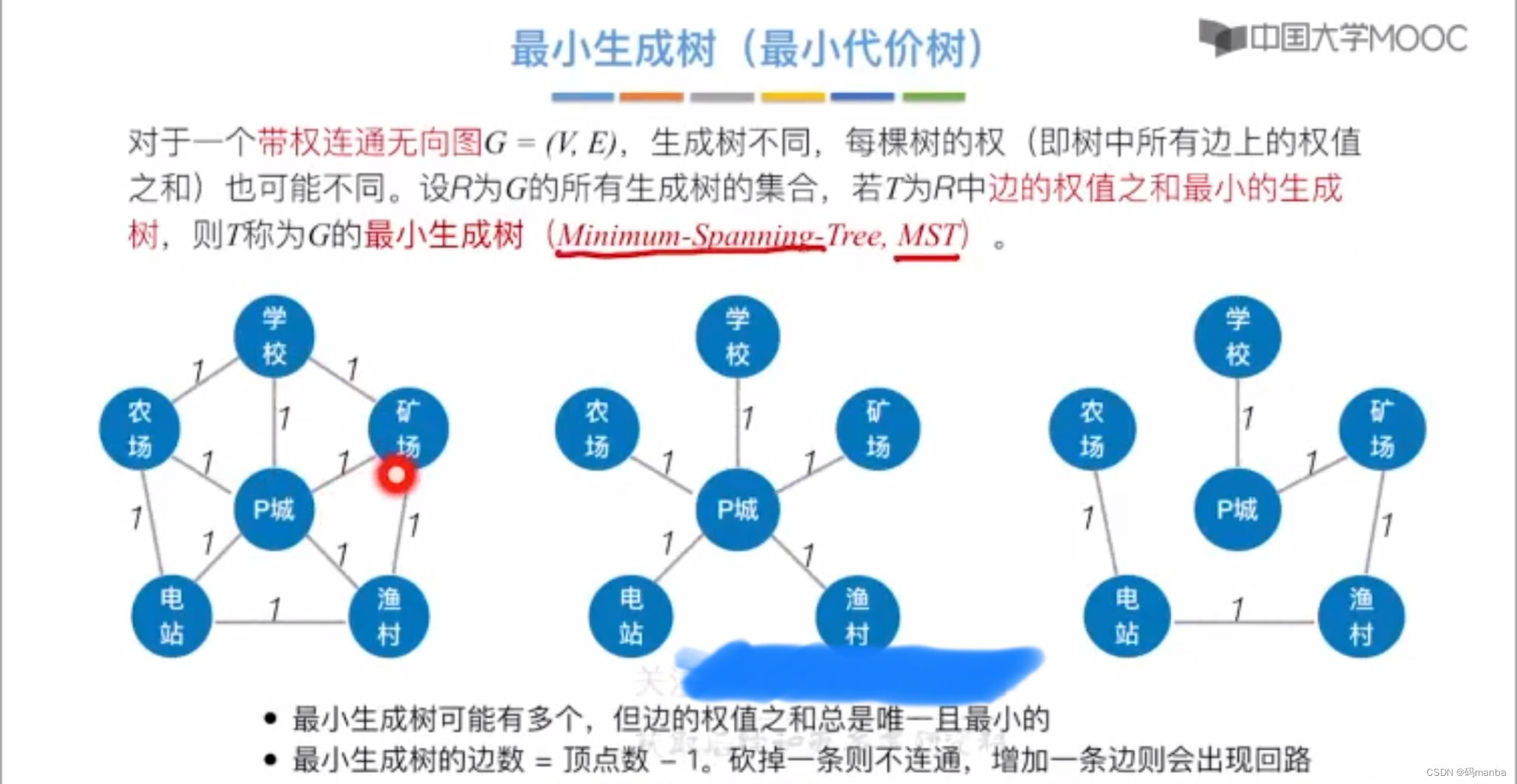
4.1 最小生成树

生成树是图的极小连通子图（区别连通分量是极大连通子图）
最小生成树也叫最小最小代价树
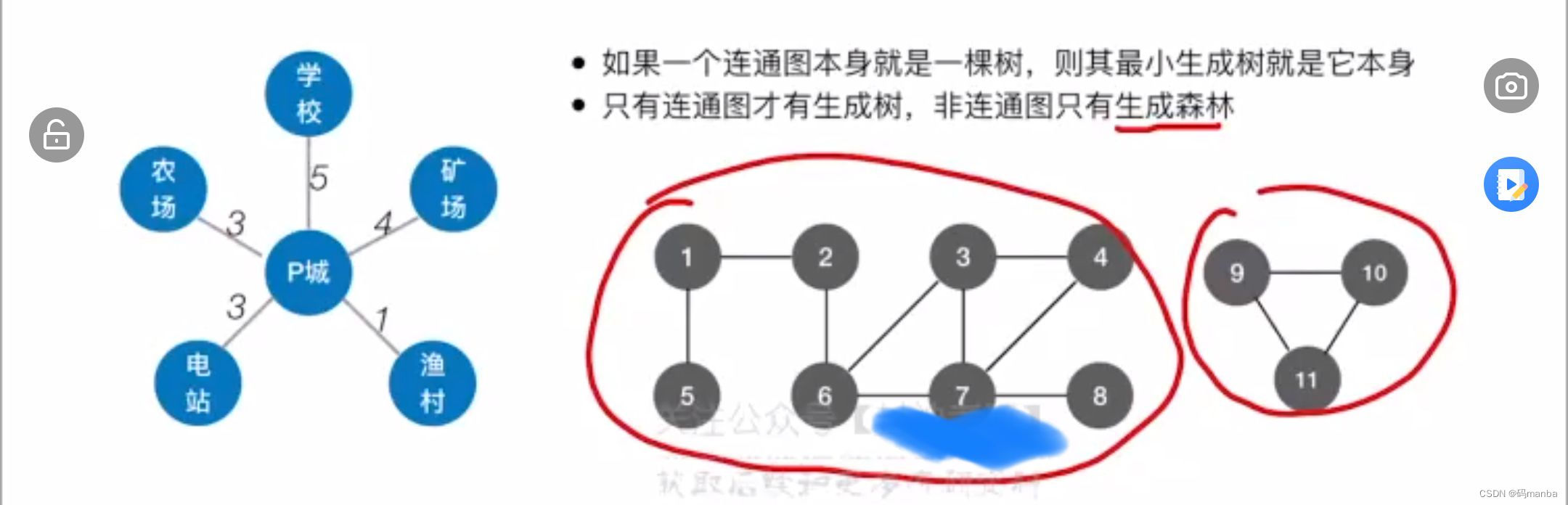
因为一个图可能会有多个生成树，找到一个各边权值和最小的一个生成树就是最小生成树

⭐ 最小生成树研究的带权的连通的无向图，因为非连通的图生成森林

1. 生成最小生成树的两大算法（普利姆、克鲁斯卡尔）

一普里姆（prim）算法

普里姆算法

• 在现有选中结点选择一个权值最小的路径所通向的未选择的结点。
• 依次将所有结点都选中
• 就是一颗最小生成树

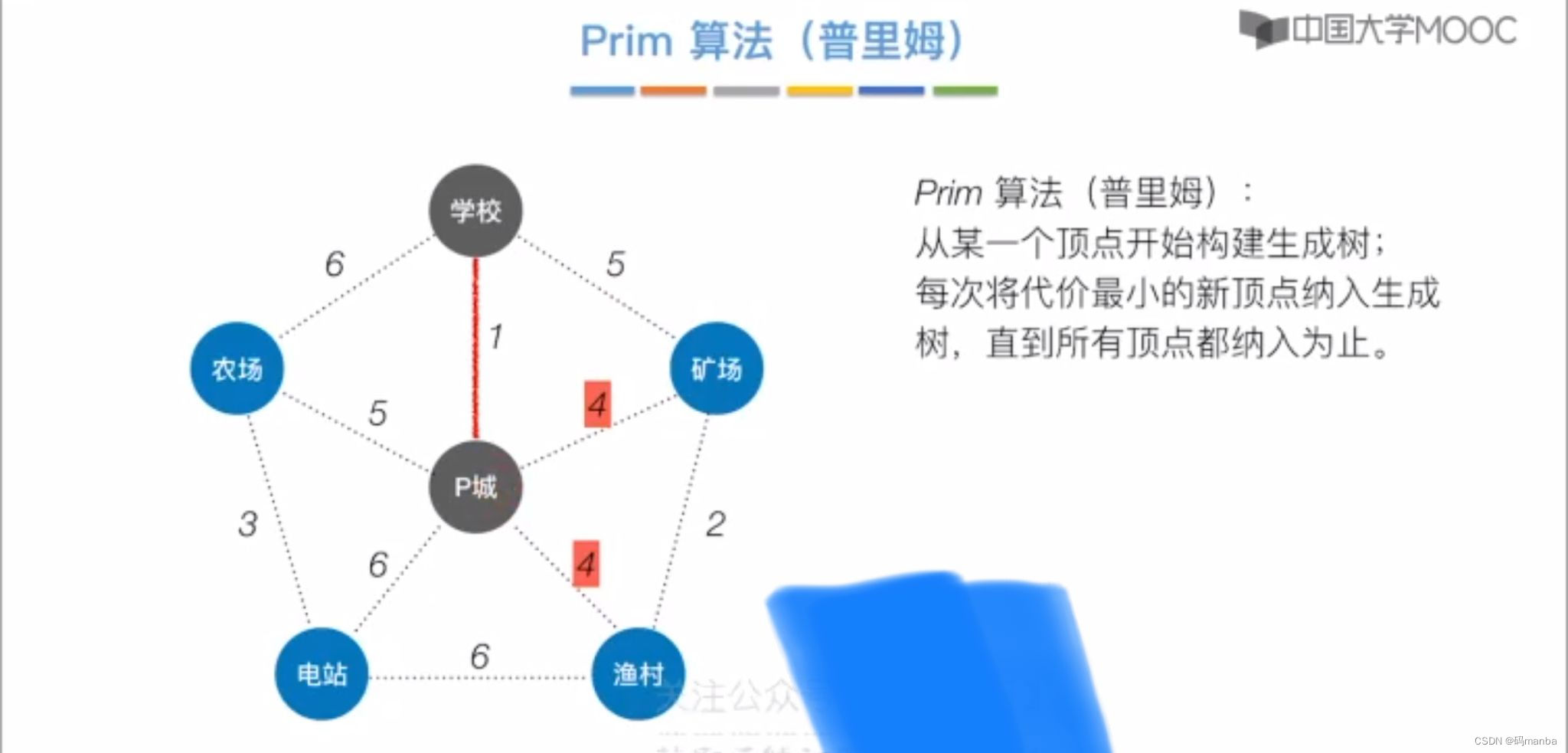
例：

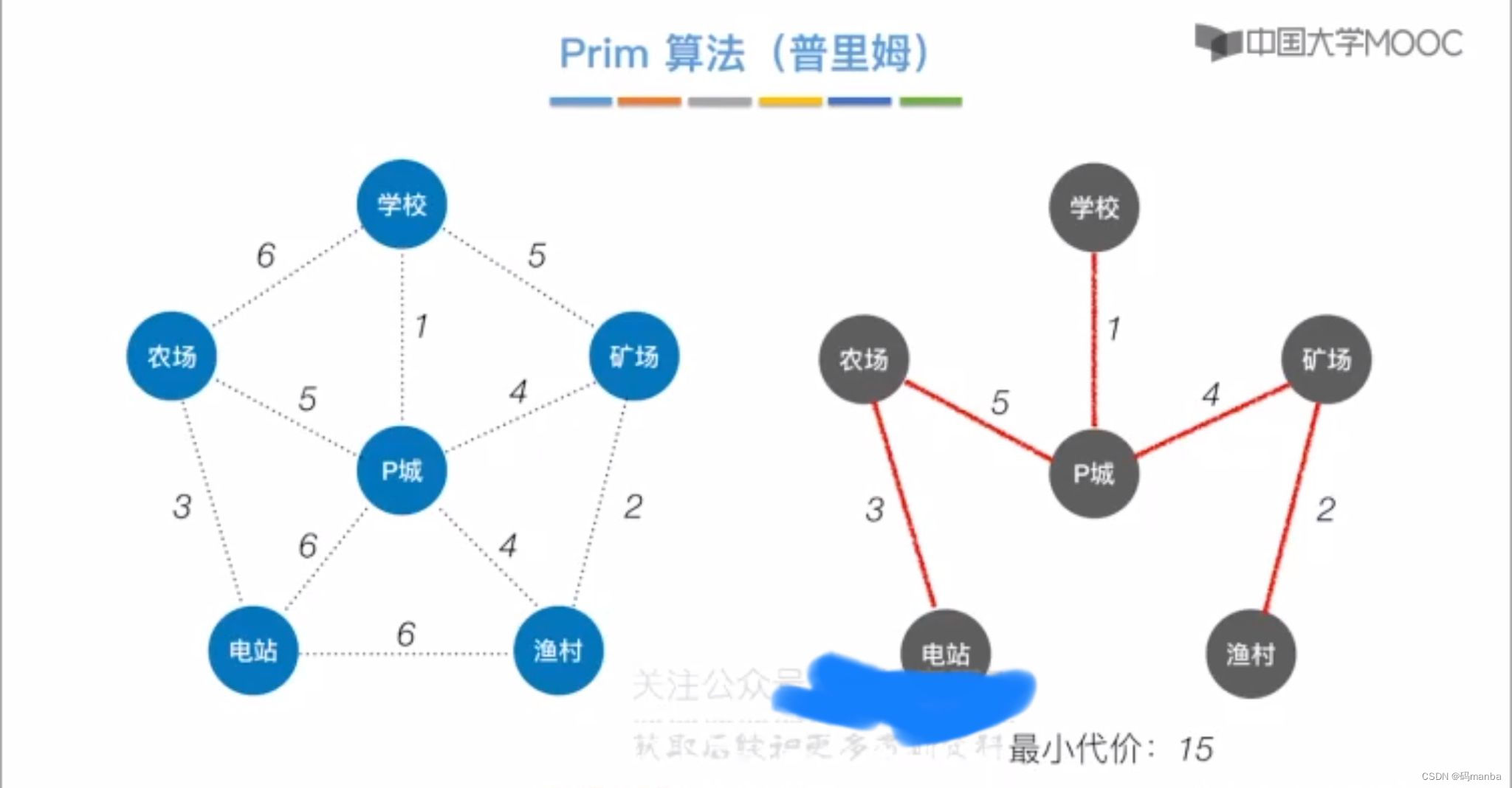
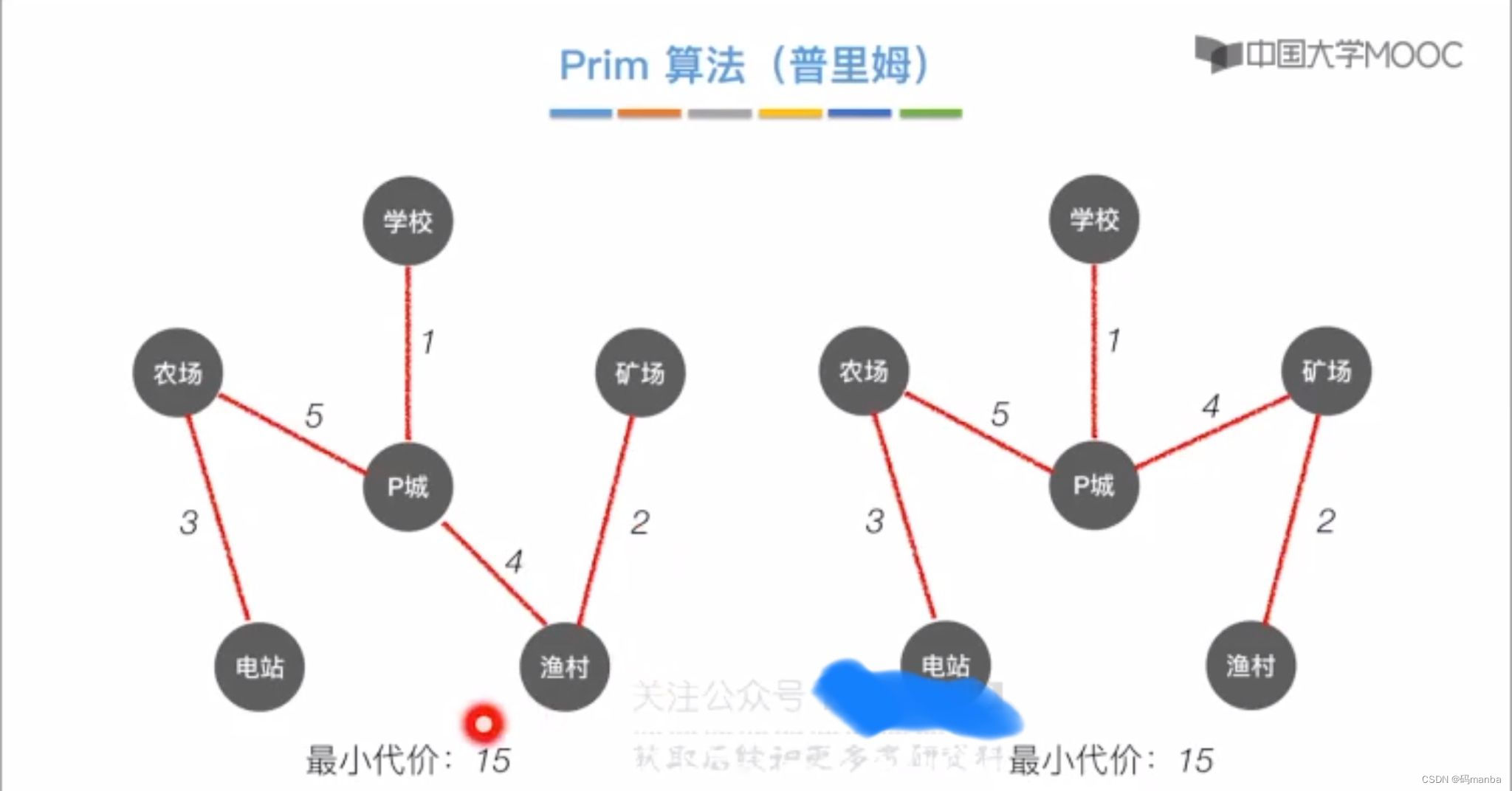
同一个图的最小生成树可能不唯一，但是权值相等。发生不唯一的可能性就是在算法进行时出现了权值相等的情况

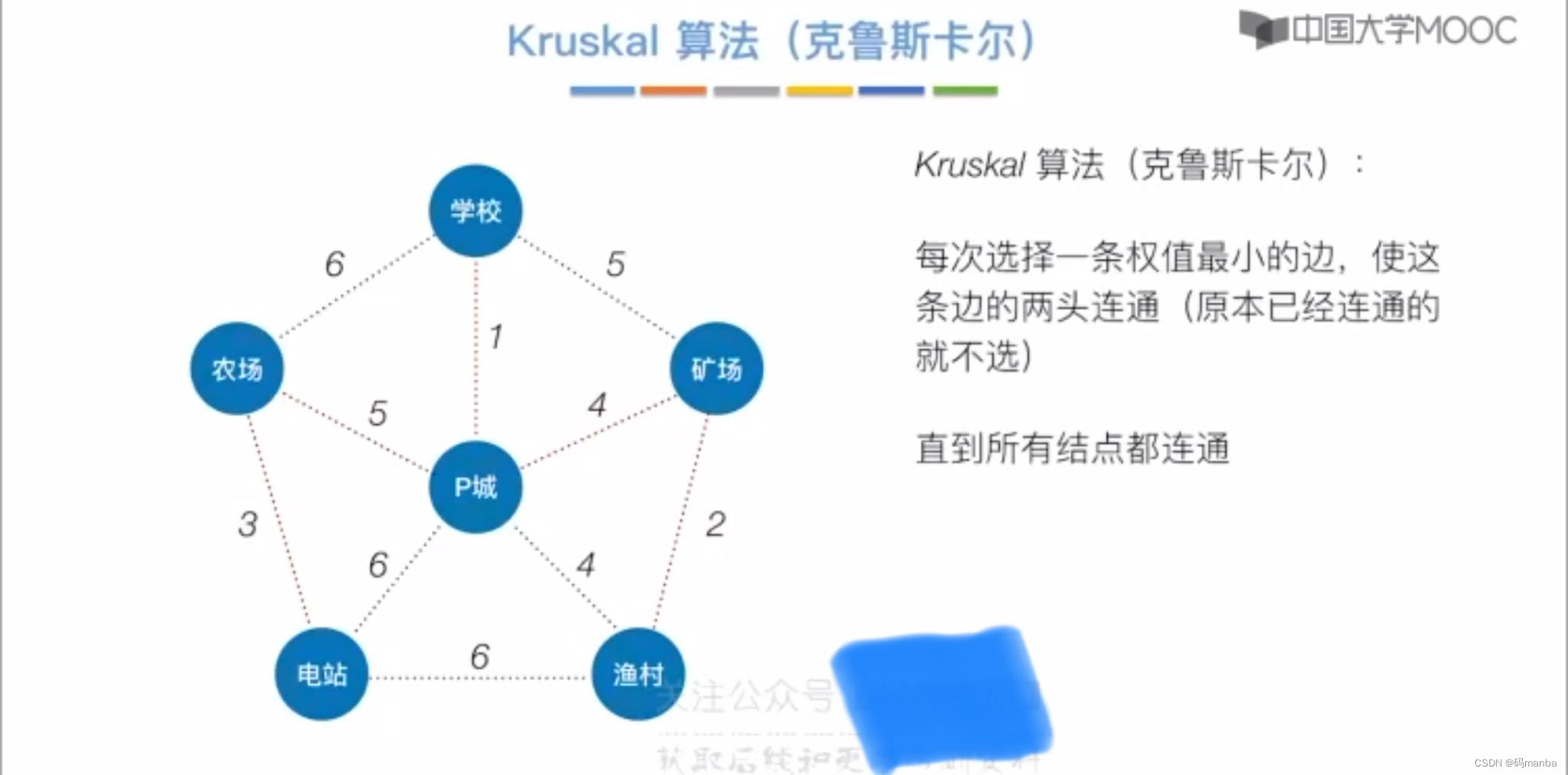
二 克鲁斯卡尔算法（kruskal）

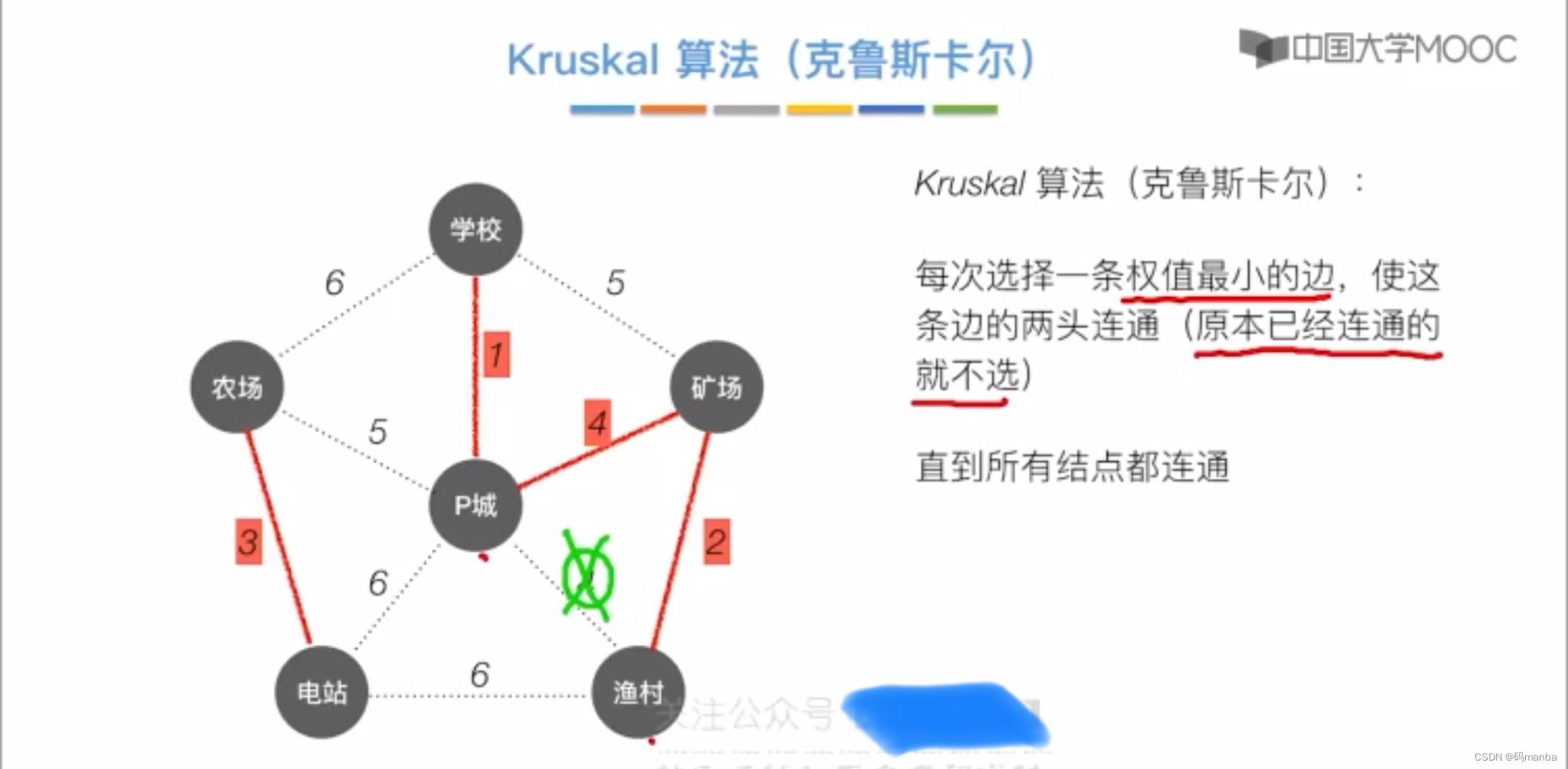
克鲁斯卡尔

• 每次选择权值最小的边，如果两个结点已经连通就不选，在选择其他边即可

2. 两个算法的时间复杂度对比

prim普里姆算法的实现思想如下

初始化

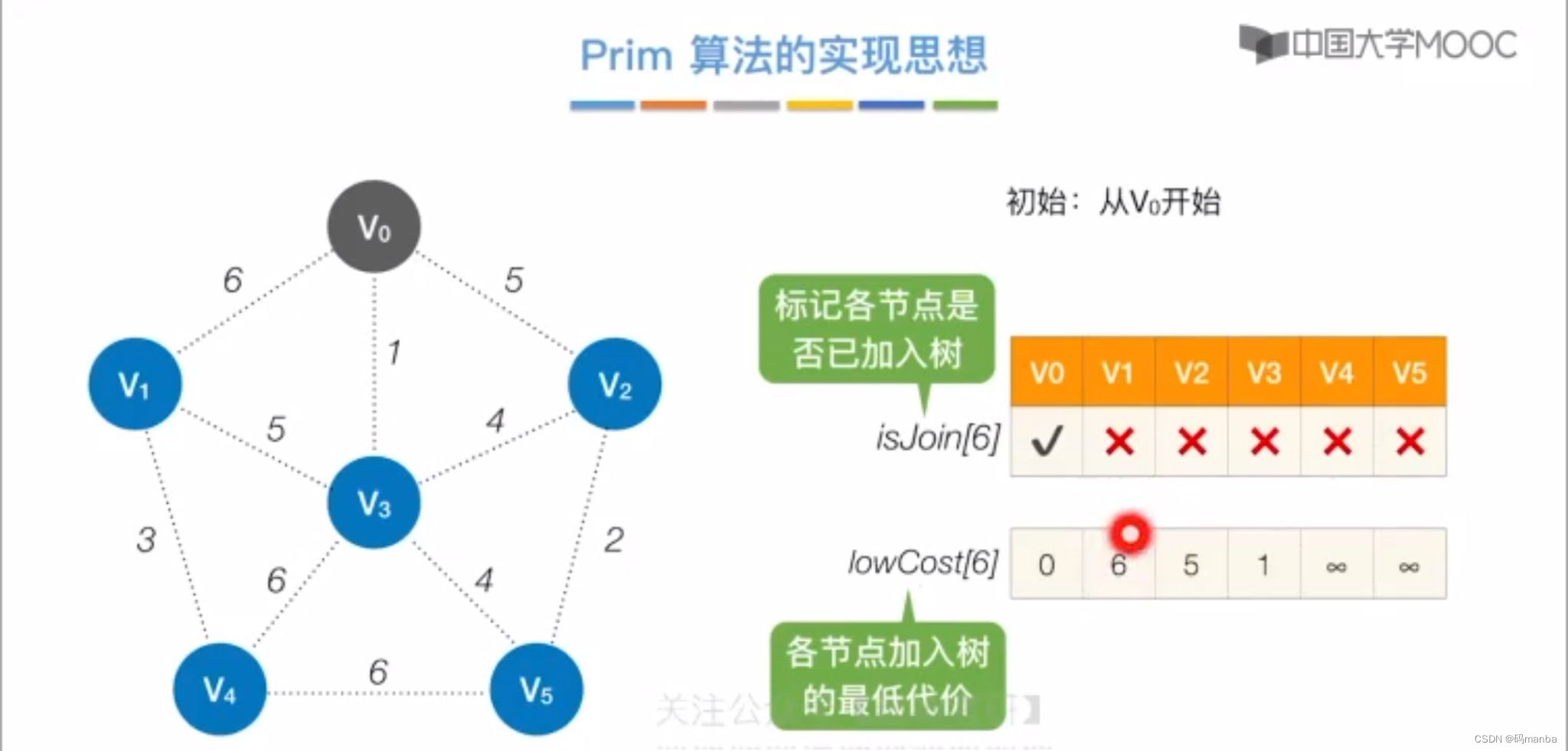
第一轮

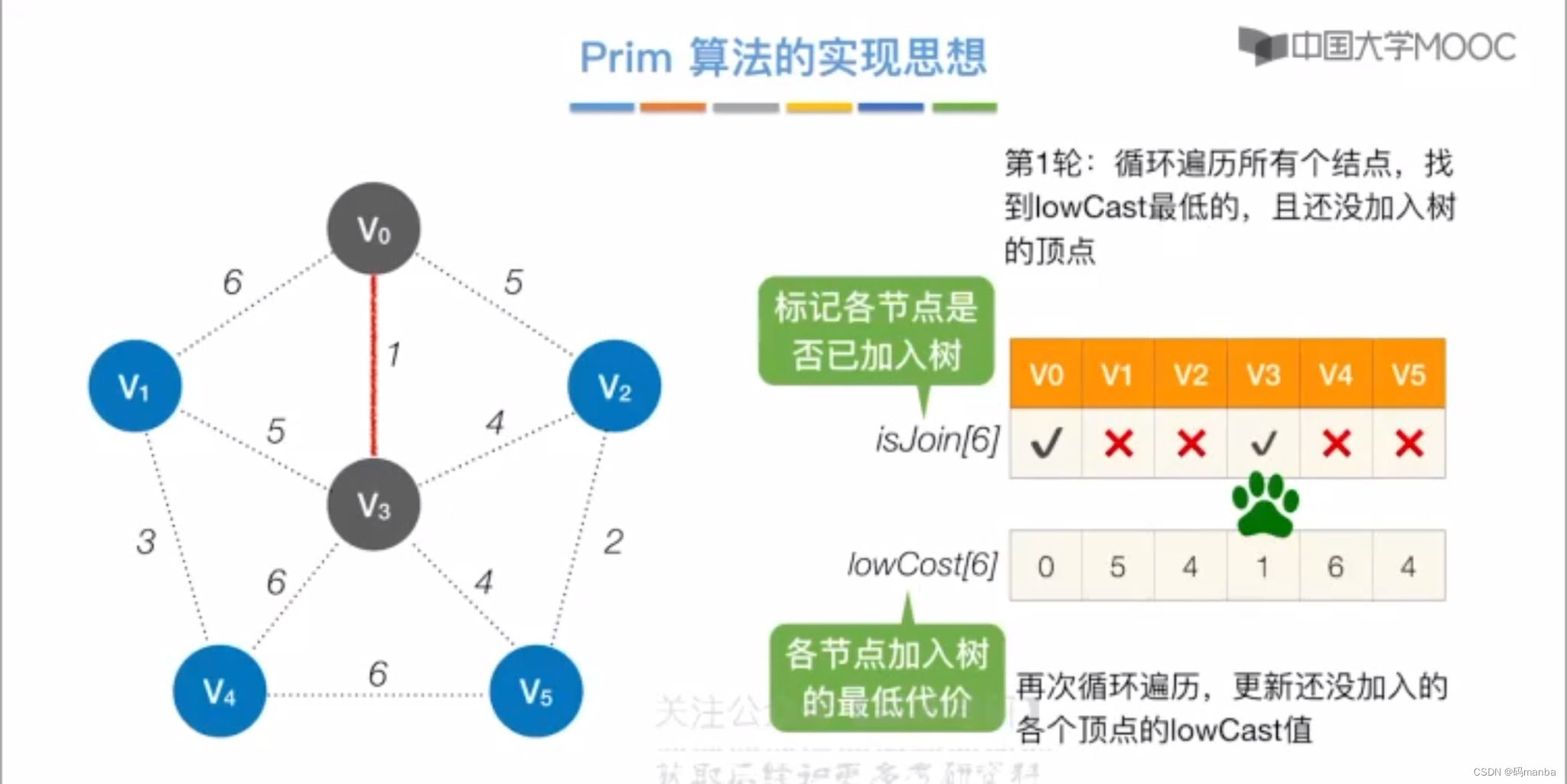
• 循环遍历找个最小权值，加入标记
• 加入后，与剩余未加入的结点间路径的权值可能会改变，所以要循环更新一下权值数组
  (注意是其余结点和新加入结点直接有没有边，如果存在边且权值更小，则应该更新权值)

克鲁斯卡尔算法实现思想

首先我们需要一个按权值排好序的数组

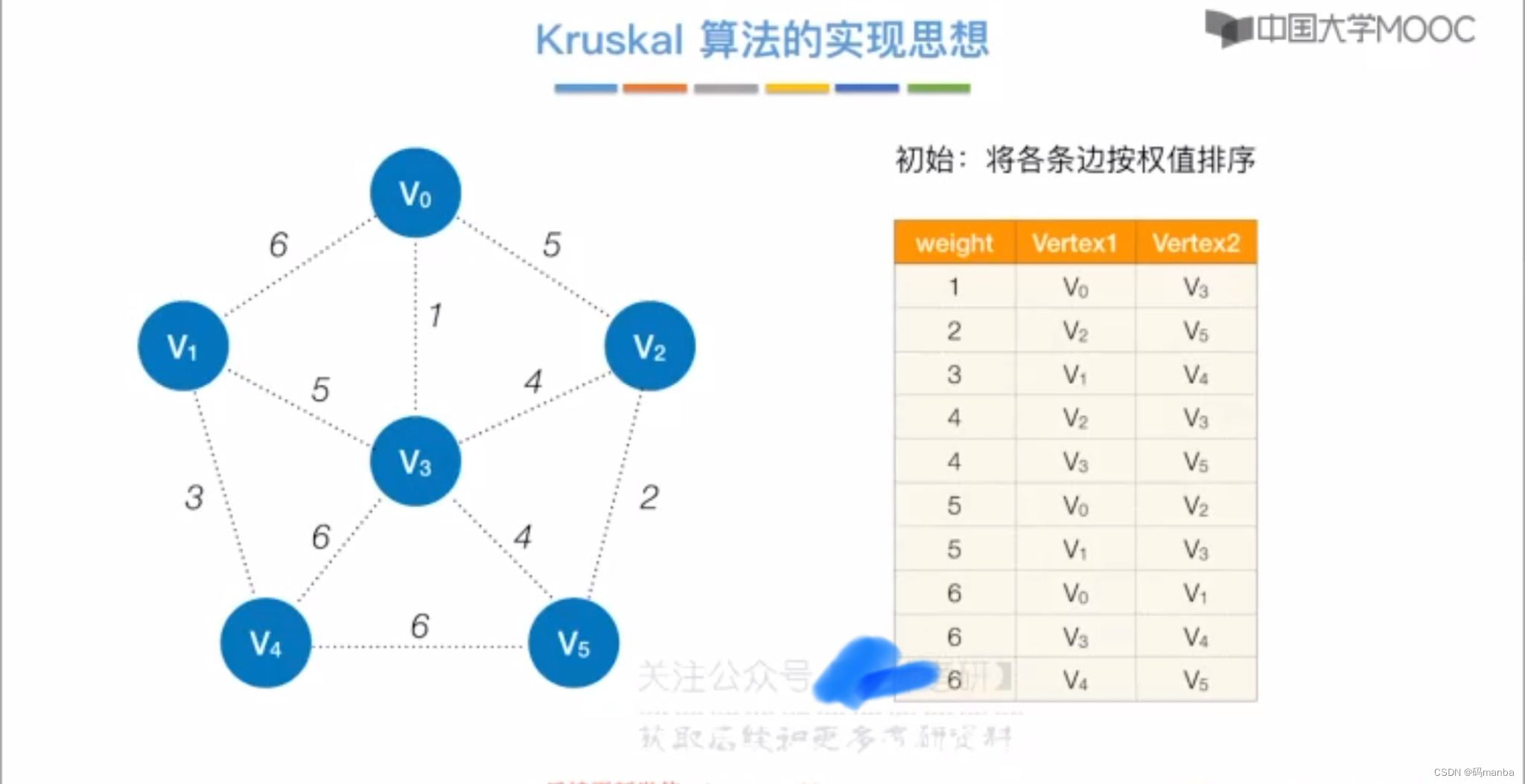
第一轮

• 我们要检查两个点之间是否连通
• 并查集操作,边的两个结点不连通，就连起来
  

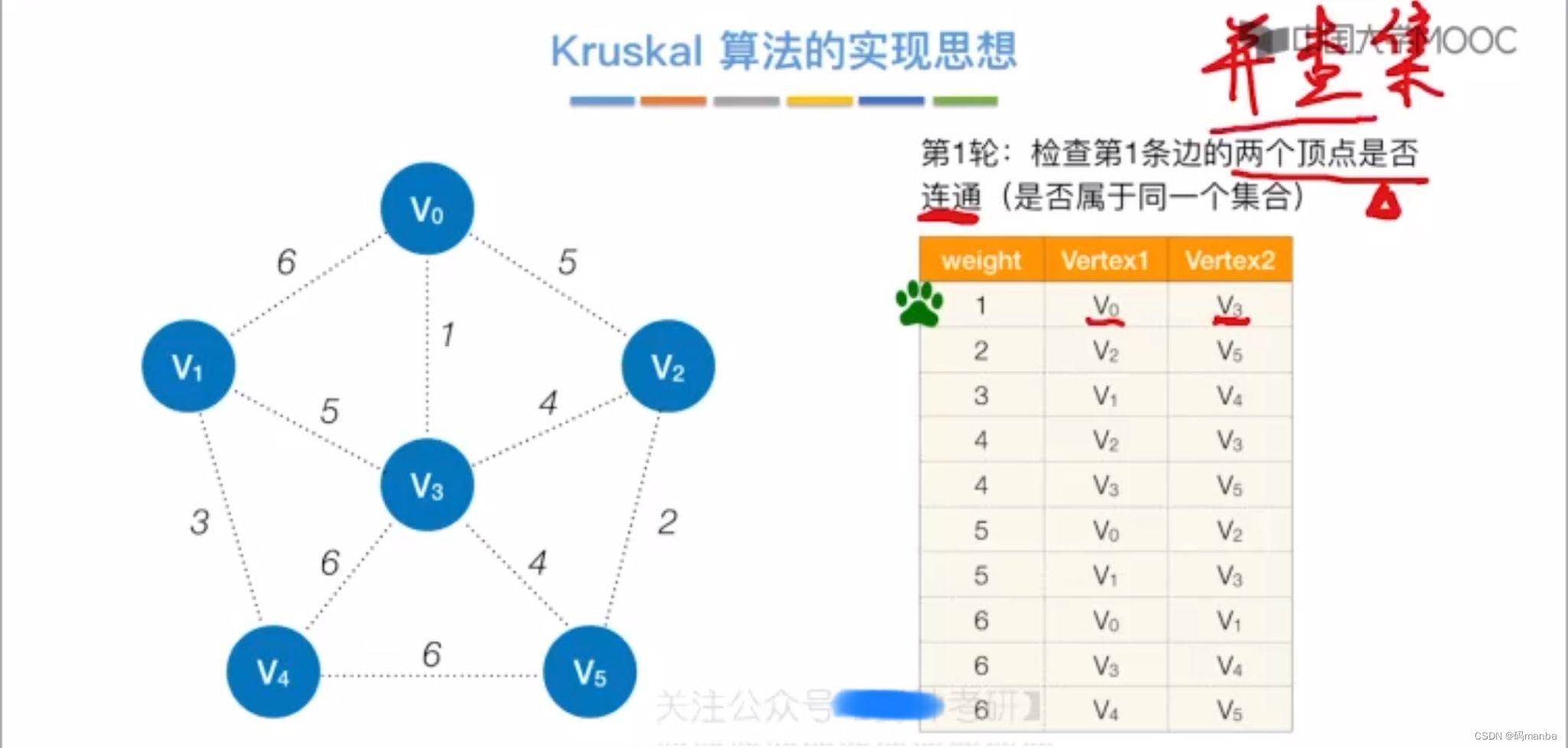
连通就跳过

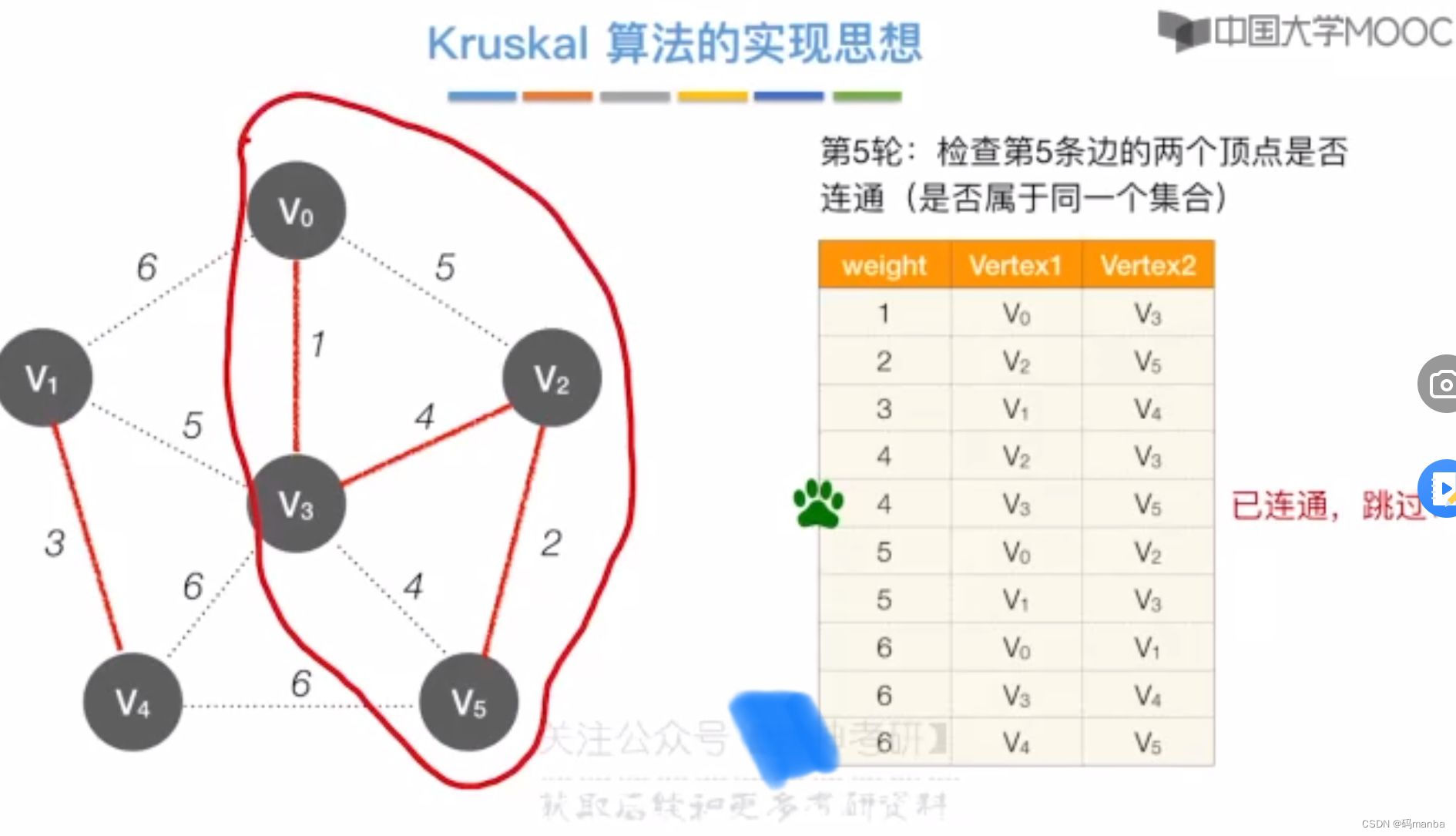
3. 最小生成树的 知识回顾

4.2 最短路径

1. 通过BFS 广度优先算法 求 最短路径 （适用于无权图） （单源最短路径）

广度优先算法的代码

⭐ 无权图的 广度优先算法

• 无权图，我们这里默认每个路径的 权值为 1
• 通过此算法，我们求得 d[] 与 path[]

其中d[] : 是 传入结点到其他结点的 长度（权值）。
path[] : 记录每个结点是由哪个结点指向的，可以逆次的依次找到 最短路径。
⭐ 因为我们是通过 BFS 求的 最短路径， 所以进行广度优先算法的时候生成的 广度优先生成树的深度一定是最小的

• 带权路径长度： 带权图的一条路径上的权值和；

2. 迪杰斯特拉算法(单源最短路径)

迪杰斯特拉

算法思想

final[]: 标记 各顶点 是否 已经 找到了 最短路径；
dist[]： 顶点最短路径的长度为多少；
path[]: 当前顶点 的前驱结点；

• 第一轮

1. 遍历所有结点， 找到未确定最短路径的，将其设置final[i] = true；
2. 因为这时候确定了一个新的最短路径的结点，检查 dist 有没有通过该结点，路径更短的情况，进而更新dist，path 数组。

接下来的每轮，都依次执行，直到不存在没有最短路径的结点， 也就是 final[]数组中不存在 false；

1. 找最短的dist对应的final设置为true； （也就是 新有一个结点确定了最短路径）
2. 更新 dist[]数组 和 path[] 数组。

算法实现

迪杰斯特拉不适合带负权值的图

负权图的应用
例如，吃鸡的时候，跑毒，直接进毒圈可能中途掉了7滴血。但是如果跑进去的过程中绕路吃了一个血包，就要掉10滴血，但是血包回5滴血。 这时候就要用负权图。

2. 弗洛伊德算法（求每点间的最短路径）

弗洛伊德

动态规划的思想

弗洛伊德算法 思想

A矩阵，是 一个二维数组，通过行列下标表示两个结点，其对应的值为两结点间的最短路径长度。
path矩阵， 用于存储两个结点直接权值最小的中转路径，动态更新。取值为 -1表示两个结点直接没有中转点，如果为其他整数表示中转点的标志。

• 第一步

1. 先让 v0可中转，检查，各结点间是否通过v0的权值更小（如果有更改A矩阵，更改path矩阵）

• 第二部

1. 再假如一个中转点，判断其他结点经过该结点有没有更短路径；从而完成对A矩阵和Path矩阵的更新。

• 经过n-1步的递推；

弗洛伊德算法可以解决 带负权图， 但 解决不了带有负权回路的图

1. 带负权的图
   
2. 带负权回路的图
   

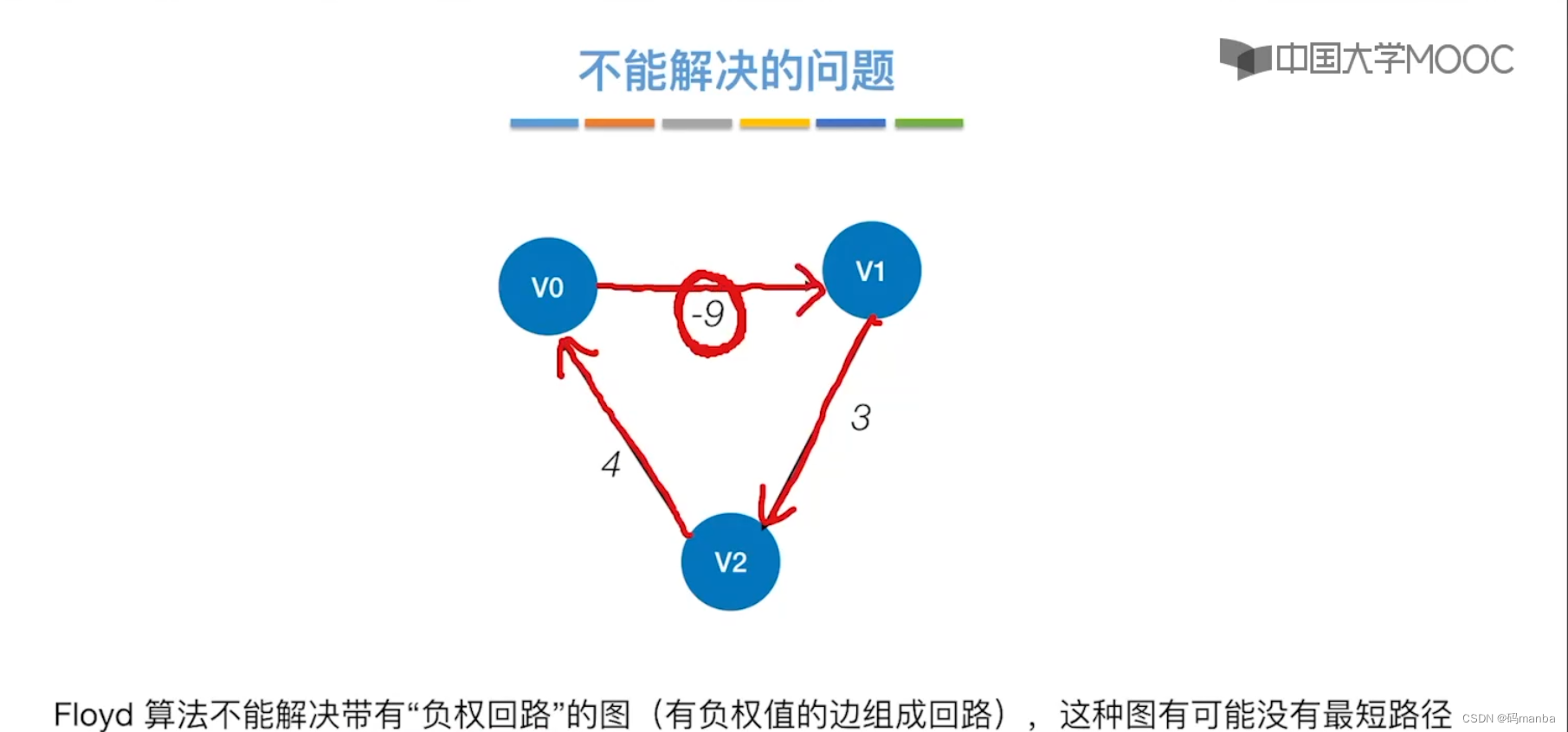
4. 三种算法的总结

4.3 有向无环图 DAG

DAG 描述 表达式

⭐ 通过有向无环图化简存储

• 就是把相同的子树通过两个路径指向，从而减少存储空间。

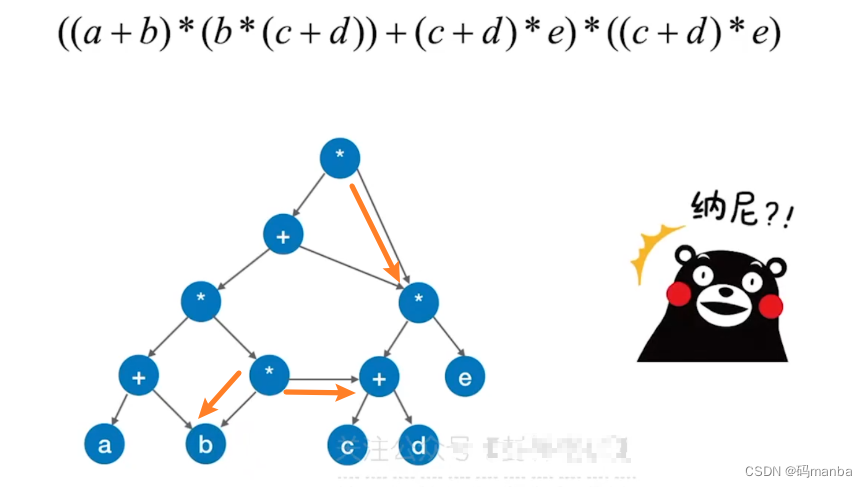
⭐（例题）DAG 表达式☞ 通过有向无环图优化 存储结点个数。

1. 问：
   
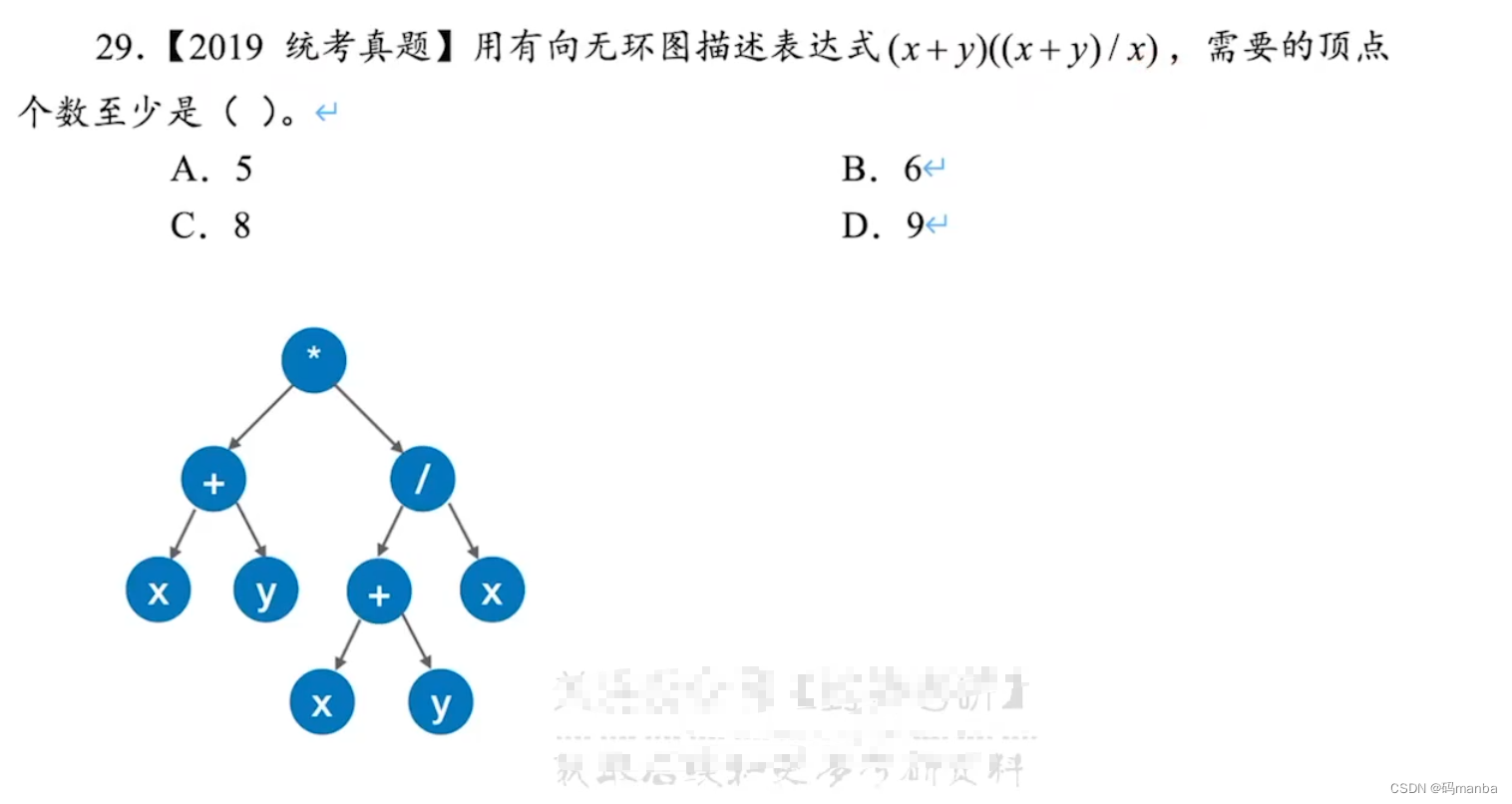
2. 答：
   
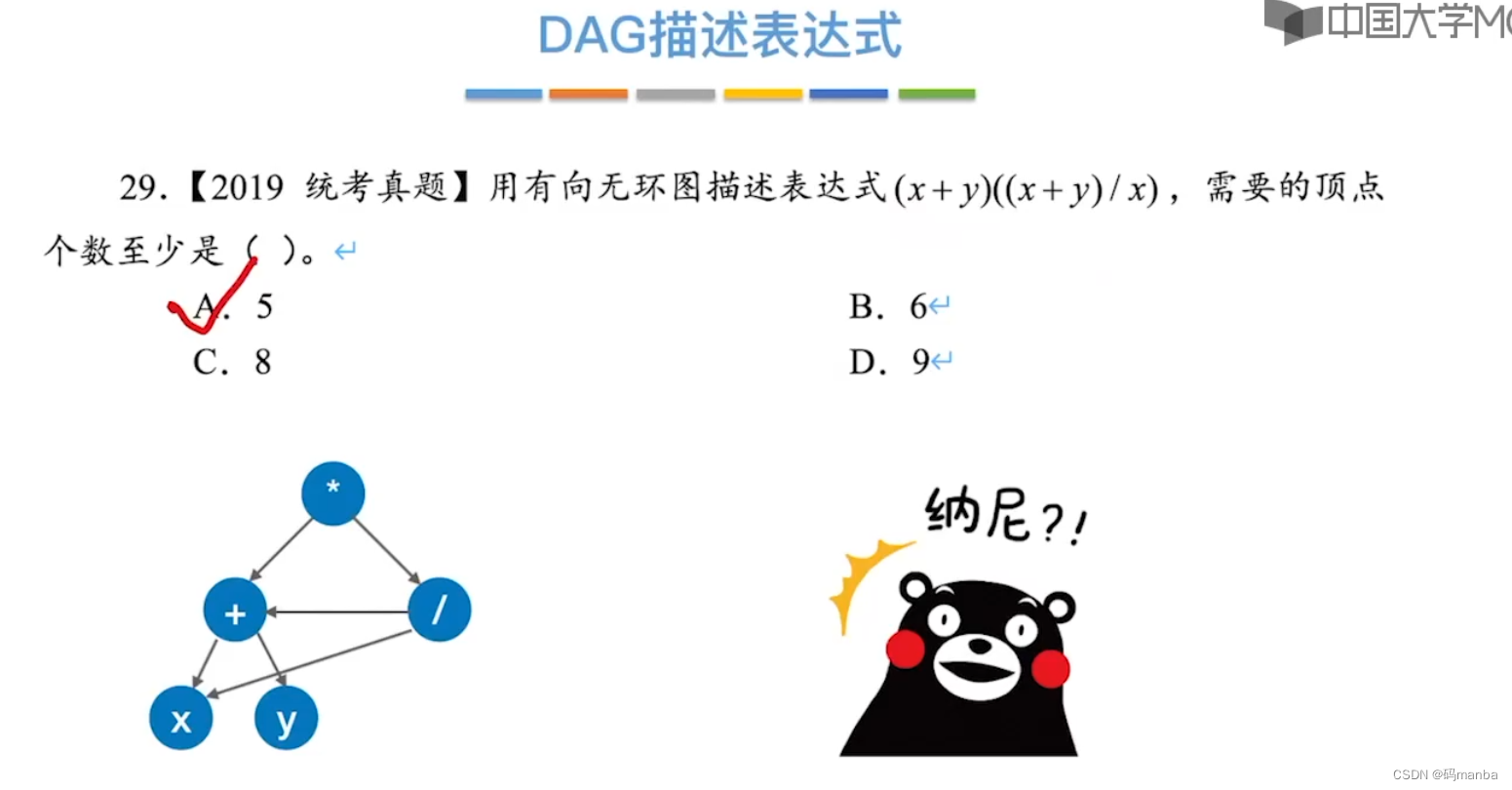
   🌙🌙 解题思路

• 在有向无环图的中的操作数是不会重复的

⭐ 先构建 DAG 图

⭐ 分层化简 可消去的结点

🌙 练习解法1

化简

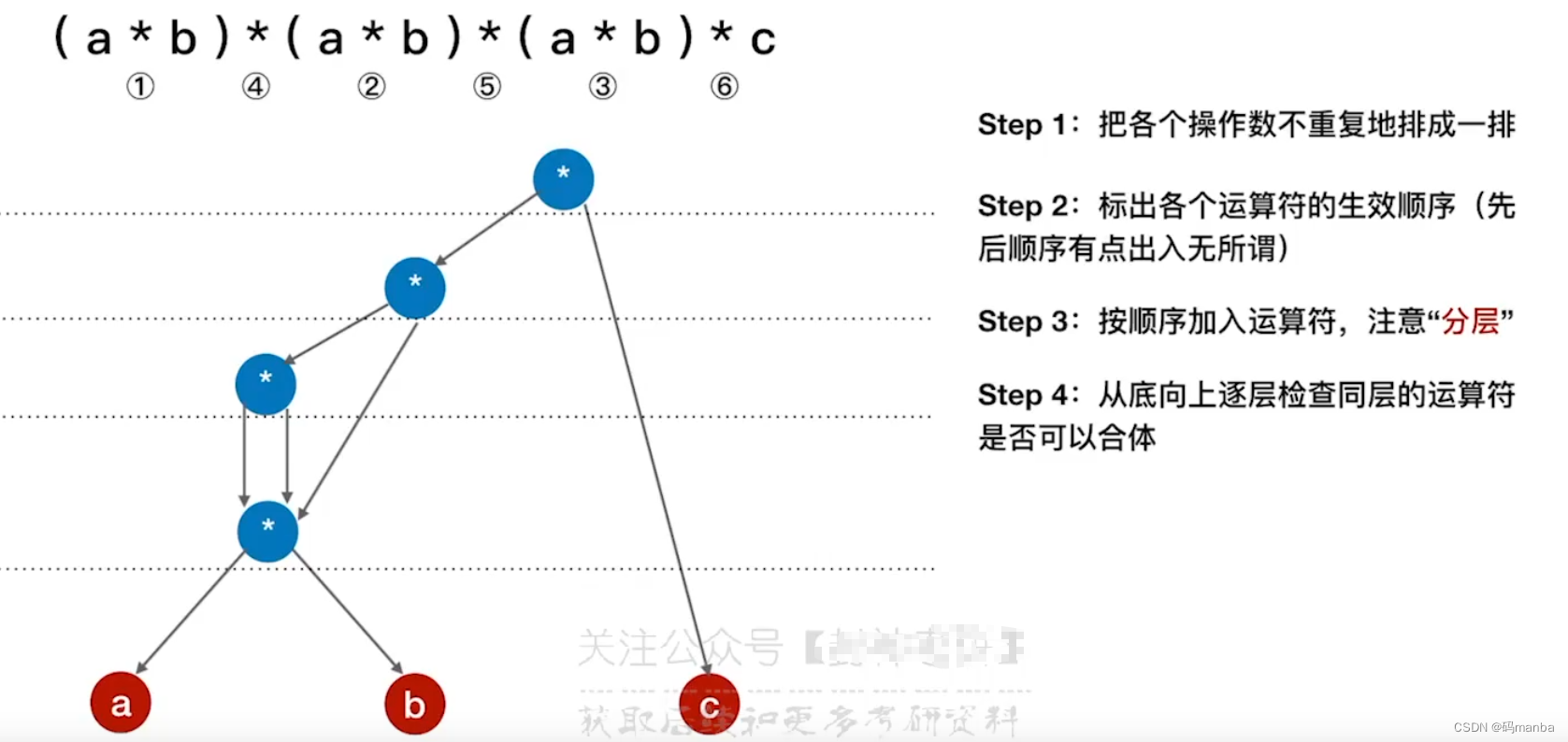
• 换一个 做法排序，结果也就不一样。
  

4.4 拓扑排序 DAG（有向无环图） 的 第二个应用

什么是 AOV网？

拓扑排序的概念

拓扑排序的实现

• 图中必须没有回路才可以进行拓扑排序。

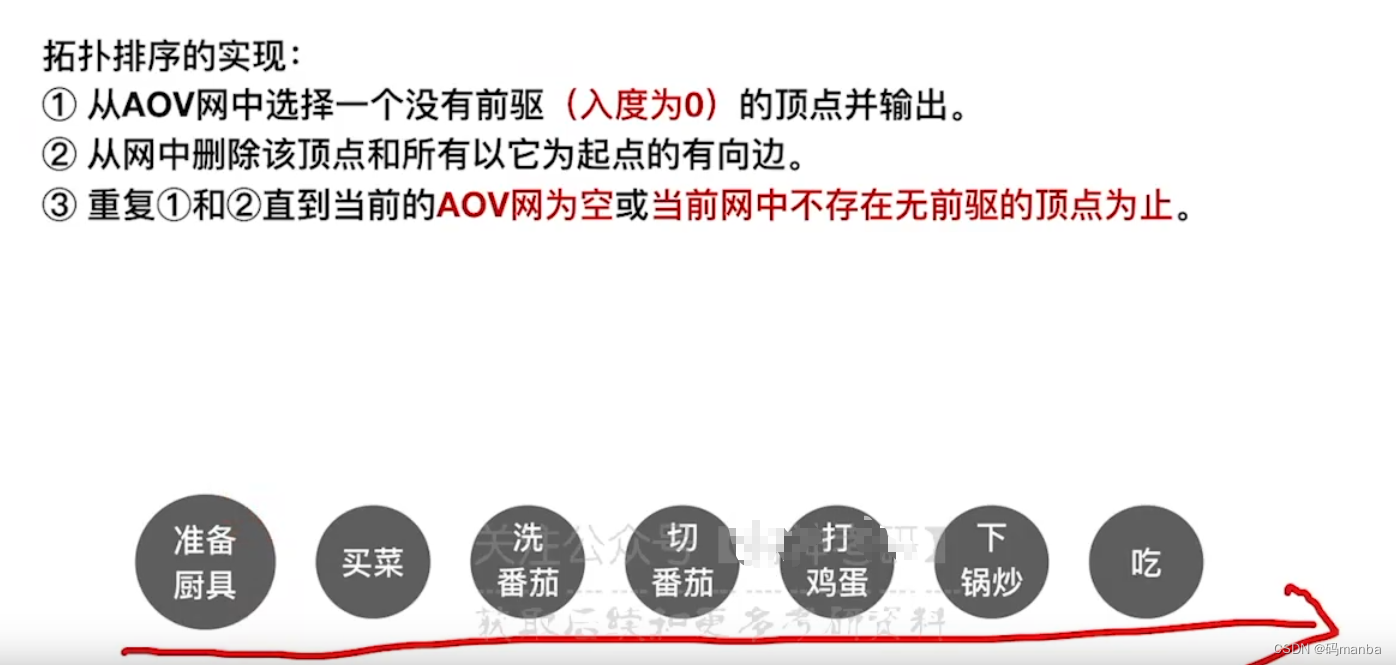
⭐⭐ 代码实现

• 思想

1. 先将入度为0的点保存到栈或者队列。

逆拓扑排序

• 检查出度为0的顶点依次输出

逆拓扑排序的实现

⭐⭐
深度优先遍历算法实现拓扑排序

拓扑排序的知识框架

4.5 关键路径

AOE 网

• 只有一个 开始结点（源点）；
• 只有一个 结束结点（汇点）；
• 有向路径：从源点到汇点的所有路径；
• 关键路径： 从源点到汇点的的所有路径中具有最大长度的路径；
• 关键活动：关键路径上的活动(弧)；

• 关键路径是最大路径长度，因此可以包含其中短的路径长度。

⭐ 事件、活动 的最早发生时间

• 事件的最早发生时间： 该事件(点) 的最早发生时间 = 指向它的事件(点) + 指向它的活动(弧)的时间；假如该事件有n个来路，那么取n个(指向它的事件最早时间 + 指向它的 活动时间)其中的最大值。
• 活动的最早发生时间： 就是这个活动的弧尾所连接的事件的最早发生时间。

⭐ 事件、活动 的最迟发生时间

• 事件的最迟发生时间： 应该按照逆拓扑排序的顺序从汇点开始计算，汇点的事件发生最迟时间 = 汇点事件最早发生时间； 按逆拓扑排序依次 每个事件的 最迟发生时间 等于 其指向的事件的最迟发生事件 减去 其指向的 活动时间； 该事件如果有n个指向， 那么取其中(指向事件最迟 - 指向活动时间) 的最小值。
• 活动的最迟开始时间： 该活动(弧) 的终点(结点)的最迟发生时间 减去 该活动(结点) 的值 所得的结果； 其实就是看这个活动所指向事件的最晚发生事件，减去该活动完成的事件，恰好到事件开始时，活动结束。

⭐ 通过 活动最早开始时间 和 活动最迟开始时间确定 关键路径！

• 时间余量： 指的是 活动的最晚开始时间减去活动的最早开始时间 所得的 时间差值。

1. 当时间余量等于0时， 指的是该活动一点都不可以拖延，就是 关键活动。
2. 关键路径就是， 时间余量等于0的 关键活动 串起来的 路径。

🌙 求关键路径的步骤

1.首先我们从源点开始，标出每个事件(点)的最早发生时间。

• 我们找到事件的最早发生时间，就等于找到了活动(弧)的最早发生时间。 它俩相等。

2.然后 我们需要从汇点开始， 推出事件(点)的最迟发生时间。

• 我们标出事件(点)的最迟发生时间后，我们就可以突出活动(弧)的最迟发生时间。

3.然后 我们就可以通过 活动的 最早、最迟开始时间，计算出时间余量；

• 时间余量等于0活动，就是关键活动， 串起来就是我们要求的关键路径。

具体步骤展开：
⭐ 1. 求所有事件的最早发生时间 ve数组。

1. 先求出图的 拓扑排序。
2. 按照拓扑排序求出事件的最早发生时间。
   • 计算每个事件的最早发生事件 = 指向该事件的最早发生事件 + 指向该事件的活动的时间；
   • 但是如果指向该事件的活动有n条， 那么 该事件的最早发生时间 是 这n个指向的(事件＋活动) 的最大值 时间。

⭐2. 求 所有事件的 最迟发生时间 ， vl数组；

1. 先求出逆拓扑序列；
2. 首先求出汇点事件的最迟发生时间，等于其事件最早发生时间。然后按照逆拓扑排序依次计算其余事件的最迟开始时间。
   • 按逆拓扑排序依次 每个事件的 最迟发生时间 等于 其指向的事件的最迟发生事件 减去 其指向的 活动时间；
   • 该事件如果有n个指向， 那么取其中(指向事件最迟 - 指向活动时间) 的最小值

⭐ 3. 活动的最早发生时间。数组e；

• 活动的最早发生时间，就是其弧尾所连接事件的最早发生事件。

⭐ 4. 活动的 最迟发生时间 数组l；

• 活动的最迟发生时间，就是 该活动弧的弧头(带箭头的一侧)所连接的 事件的最迟发生时间 减去 该活动的权值。

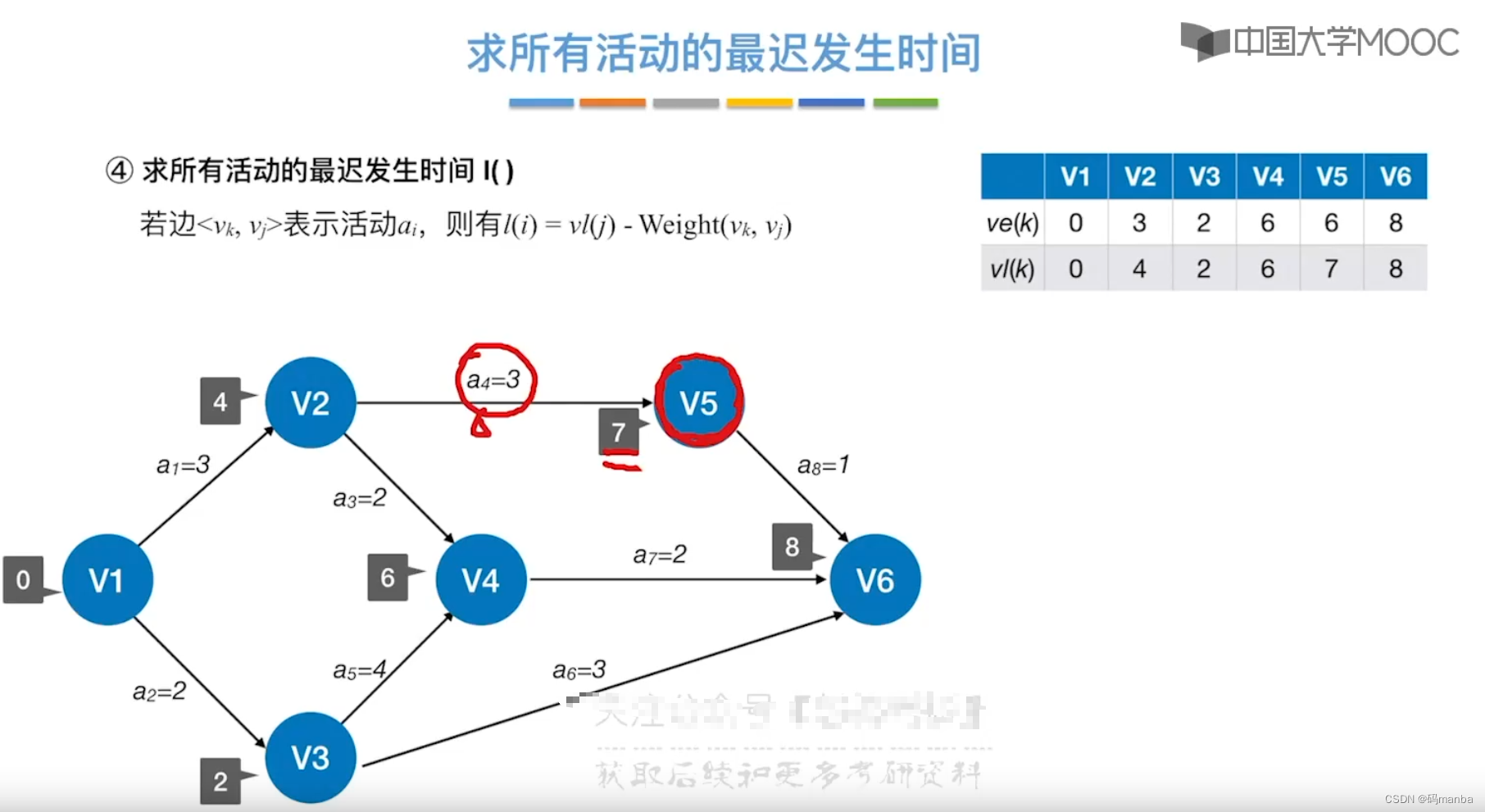
⭐5. 时间余量

• 时间余量 = 活动最迟发生时间 减去 活动最早发生时间；
  • 时间余量等于0，指关键活动；
  • 根据关键活动，我们就找到了关键路径；

关键活动和关键路径的部分特性

⭐ 关键活动改变时间，会影响项目工期； 当压缩过度可能会使关键路径不再是关键路径。

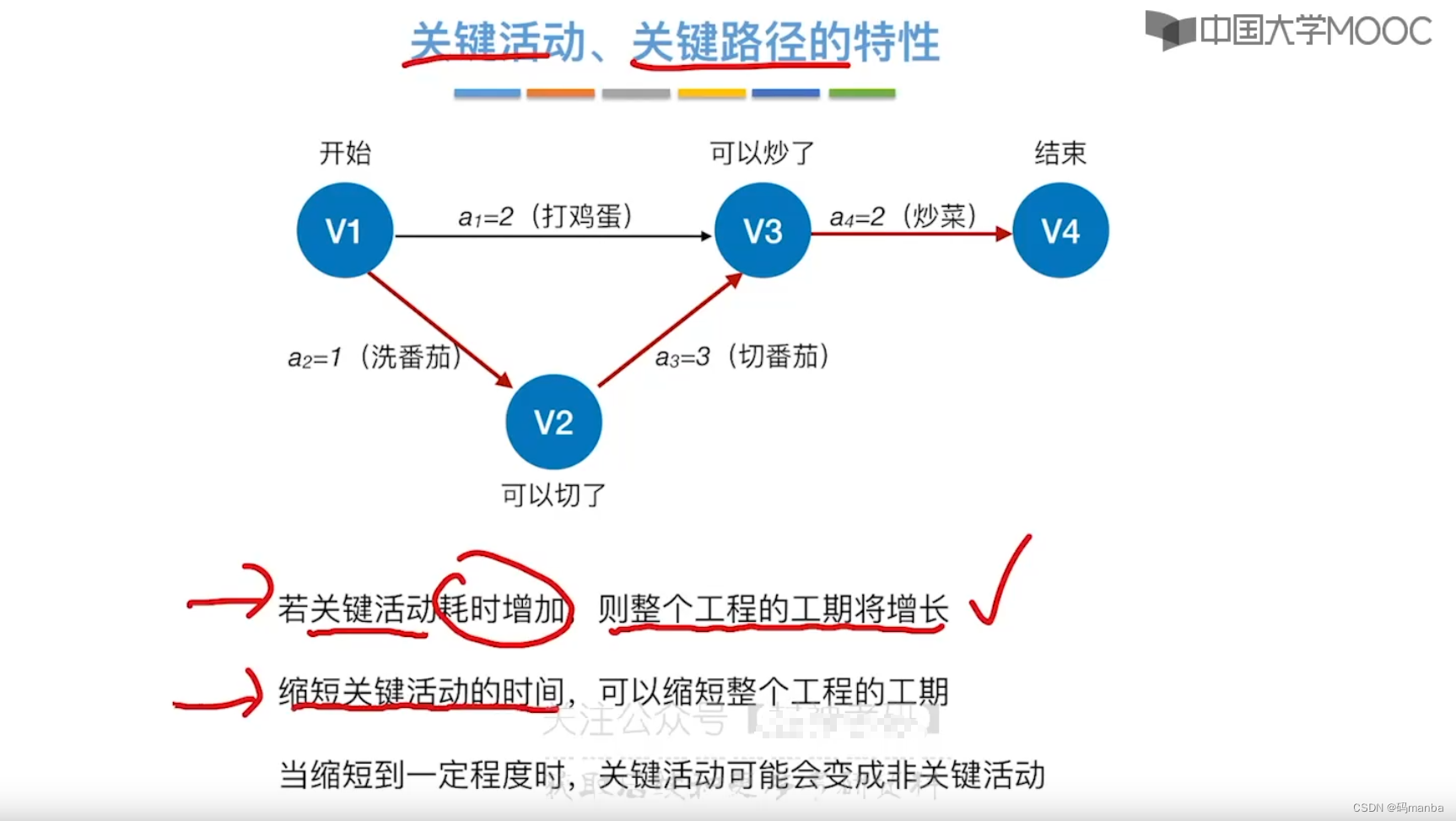
⭐ AOE网中可能存在多条关键路径，因此如果想改变工期，可以同时压缩不同的两个不在一个关键路径上的关键活动时间，或者压缩一条在同一个关键路径的关键活动。

AOE网知识框架