深度学习入门-神经网络的学习

​ 这里所说的“学习”是指从训练数据中 自动获取最优权重参数的过程。为了使神经网络能进行学习，将导 入损失函数这一指标。而学习的目的就是以该损失函数为基准，找出能使它的值达到最小的权重参数。

神经网络(深度学习)与机器学习的不同

​ 如图所示，神经网络直接学习图像本身。在第2个方法，即利用特征量和机器学习的方法中，特征量仍是由人工设计的，而在神经网络中，连 图像中包含的重要特征量也都是由机器来学习的。

损失函数

​ 损失函数是表示神经网络性能的“恶劣程度”的指标，即当前的 神经网络对监督数据在多大程度上不拟合，在多大程度上不一致。这个损失函数可以使用任意函数， 但一般用均方误差和交叉熵误差等。

均方误差

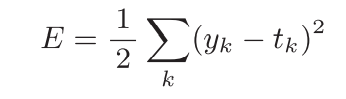
​ 这里，yk是表示神经网络的输出，tk表示正确解的标签，k表示数据的维数。

#手写数字识别中的以均方误差为损失函数的例子
import numpy as np

def mean_squared_error(y, t):
    return 0.5 * np.sum((y-t)**2)

y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])#图像为各个数字的概率
t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0])#已知的正确解的标签

print(mean_squared_error(y, t))
1
2
3
4
5
6
7
8
9
10

交叉熵误差

这里，log表示以e为底数的自然对数（log e ）。yk是神经网络的输出，tk是 正确解标签。由于只有正确解的标签tk为1，所以交叉熵误差的值是由正确解标签所对应的输出结果决定的。

import numpy as np

def cross_entropy_error(y, t):
    delta = 1e-7
    return -np.sum(t * np.log(y + delta))

y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])
t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0])

print(cross_entropy_error(y, t))
1
2
3
4
5
6
7
8
9
10

mini-batch学习

​ 前面介绍的损失函数的例子中考虑的都是针对单个数据的损失函数。如果要求所有训练数据的损失函数的总和，以交叉熵误差为例，可以写成下面的式，该式子是将N个单个数据的损失函数值加到了一起，最后除N进行正规化。

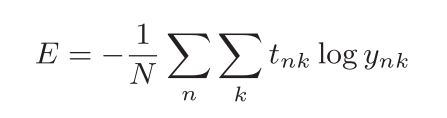
​ 但是对于具有大量数据的模型，计算所有对象的损失函数是不现实的，所以我们引入了mini-batch学习方法。所谓mini-batch学习，就是从所有的训练数据中随机选择若干个作为代表，进行计算。

​ 那么，如何从这个训练数据中随机抽取部分数据呢？我们可以使用 NumPy的np.random.choice()，写成如下形式。

train_size = x_train.shape[0] 
batch_size = 10 
batch_mask = np.random.choice(train_size, batch_size) #使用np.random.choice()可以从指定的数字中随机选择想要的数字。比如，np.random.choice(60000, 10)会从0到59999之间随机选择10个数字。
x_batch = x_train[batch_mask] #batch_mask 数组中保存的是索引值
t_batch = t_train[batch_mask]
1
2
3
4
5

数值微分

数值微分与解析性求导

def numerical_diff(f, x):
    h = 1e-4 # 0.0001
    return (f(x+h) - f(x-h)) / (2*h)
1
2
3

​ 如上所示，利用微小的差分求导数的过程称为数值微分（numerical  differentiation）。而基于数学式的推导求导数的过程，则用“解析 性”（analytic）一词，称为“解析性求解”或者“解析性求导”。比如， y = x^2 的导数，可以通过 y=2*x 解析性地求解出来。因此，当x = 2时， y的导数为4。解析性求导得到的导数是不含误差的“真的导数”。

对于以上函数，利用数值微分的求解 x=5,x=10 的结果为：

解析性求解的结果为：
$$f^{‘}(5)=0.2$$

$$f^{‘}(10)=0.3$$

和上面的结果相比，我们发现虽然 严格意义上它们并不一致，但误差非常小。实际上，误差小到基本上可以认 为它们是相等的。

梯度

def numerical_gradient(f, x):
 h = 1e-4 # 0.0001
 grad = np.zeros_like(x) # 生成和x形状相同的数组
 for idx in range(x.size):
    tmp_val = x[idx]
    # f(x+h)的计算
    x[idx] = tmp_val + h
    fxh1 = f(x)
    # f(x-h)的计算
    x[idx] = tmp_val - h
    fxh2 = f(x)
    grad[idx] = (fxh1 - fxh2) / (2*h)
    x[idx] = tmp_val # 还原值
 return grad
1
2
3
4
5
6
7
8
9
10
11
12
13
14

$$我们把f(x_0+x_1)=x_0^2+x_1^2的梯度画在图上如下(这里我们画的是元素值为负梯度的向量)$$

​ 由图可知，箭头指向该函数值最小的地方。但并非任何时候都这样。实际上， 梯度会指向各点处的函数值降低的方向。更严格地讲，梯度指示的方向 是各点处的函数值减小最多的方向 。

梯度法

​ 在神经网络的学习中，要想获得最大的精度，就要想办法使损失函数的值降到最小。为了求得损失函数的最小值，我们可以使用梯度法，虽然梯度的方向并不一定指向最小值，但沿着它的方向能够最大限度地 减小函数的值。因此，在寻找函数的最小值（或者尽可能小的值）的位置的 任务中，要以梯度的信息为线索，决定前进的方向。

​ 在梯度法中，函数的取值从当前位置沿着梯度方向前进一定距离，然后在新的地方重新求梯度，再沿着新梯度方向前进， 如此反复，不断地沿梯度方向前进。像这样，通过不断地沿梯度方向前进， 逐渐减小函数值的过程就是梯度法（gradient method）。梯度法是解决机器学习中最优化问题的常用方法，特别是在神经网络的学习中经常被使用。

​ 用数学公式来表示梯度法，如下所示：

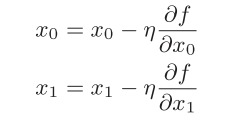
​ 式中的η表示更新量，在神经网络的学习中，称为学习率（learning rate）。学习率决定在一次学习中，应该学习多少，以及在多大程度上更新参数。

​ 式子是表示更新一次的式子，这个步骤会反复执行。也就是说，每 一步都按式更新变量的值，通过反复执行此步骤，逐渐减小函数值。 虽然这里只展示了有两个变量时的更新过程，但是即便增加变量的数量，也 可以通过类似的式子（各个变量的偏导数）进行更新。

​ 用Python实现梯度下降的例子

import numpy as np

def numerical_gradient(f, x): #求偏导
 h = 1e-4 # 0.0001
 grad = np.zeros_like(x) # 生成和x形状相同的数组
 for idx in range(x.size):
    tmp_val = x[idx]# f(x+h)的计算
    x[idx] = tmp_val + h
    fxh1 = f(x)# f(x-h)的计算
    x[idx] = tmp_val - h
    fxh2 = f(x)
    grad[idx] = (fxh1 - fxh2) / (2*h)
    x[idx] = tmp_val # 还原值
 return grad

def gradient_descent(f,init_x,lr=0.01,step_num=100): #梯度下降更新过程
    x = init_x
    for i in range(step_num):
        grad = numerical_gradient(f, x)
        x -= lr*grad
    return x

def fun(x):
    return x[0]**2+x[1]**2

init_x = np.array([-3.0,4.0])
print(gradient_descent(fun,init_x,0.1,100))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

神经网络的梯度

​ 对于神将网络而言，我们要求的梯度是损失函数关于权重的梯度。

代码实现

import numpy as np

def _numerical_gradient_1d(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x)
    

    for idx in range(x.size):
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x) # f(x+h)
        
        x[idx] = tmp_val - h 
        fxh2 = f(x) # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)
        
        x[idx] = tmp_val # 还原值
        
    return grad


def numerical_gradient_2d(f, X):
    if X.ndim == 1:
        return _numerical_gradient_1d(f, X)
    else:
        grad = np.zeros_like(X)
        

        for idx, x in enumerate(X):
            grad[idx] = _numerical_gradient_1d(f, x)
        
        return grad

def cross_entropy_error(y, t):
    delta = 1e-7
    return -np.sum(t * np.log(y + delta))

def softmax(a):
    exp_a = np.exp(a - np.max(a))
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    return y

class simpleNet:
    def __init__(self):
        self.W = np.random.randn(2,3) # 用高斯分布进行初始化
    def predict(self, x):
        return np.dot(x, self.W)
    def loss(self, x, t):
        z = self.predict(x)
        y = softmax(z)
        loss = cross_entropy_error(y, t)
        return loss

def f(W):
    return net.loss(x, t)

net = simpleNet()
x = np.array([0.6,0.9])
t = np.array([0,0,1])
dW = numerical_gradient_2d(f, net.W)
print(dW)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

学习算法的实现

前提

神经网络存在合适的权重和偏置，调整权重和偏置以便拟合训练数据的 过程称为“学习”。神经网络的学习分成下面4个步骤。

步骤1（mini-batch）

从训练数据中随机选出一部分数据，这部分数据称为mini-batch。我们 的目标是减小mini-batch的损失函数的值。

步骤2（计算梯度）

为了减小mini-batch的损失函数的值，需要求出各个权重参数的梯度。 梯度表示损失函数的值减小最多的方向。

步骤3（更新参数）

将权重参数沿梯度方向进行微小更新。

步骤4（重复）

重复步骤1、步骤2、步骤3。

2层神经网络的类

import sys, os
sys.path.append(os.pardir)
from common.functions import sigmoid,softmax,cross_entropy_error
from common.gradient import numerical_gradient
import numpy as np

class TwoLayerNet:
    def __init__(self, input_size, hidden_size, output_size,weight_init_std=0.01):
        # 初始化权重
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)

    def predict(self, x):
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']
        a1 = np.dot(x, W1) + b1
        z1 = sigmoid(a1)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)
        return y
    
    def loss(self, x, t):
        y = self.predict(x)
        return cross_entropy_error(y, t)
    
    def accuracy(self, x, t): #计算预测的精度
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        t = np.argmax(t, axis=1)
        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy
    
    def numerical_gradient(self, x, t): #计算梯度
        loss_W = lambda W: self.loss(x, t)
        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
        return grads

net = TwoLayerNet(input_size=784, hidden_size=100, output_size=10)
x = np.random.rand(100,784)
t = np.random.rand(100,10)
grads = net.numerical_gradient(x, t)
print(grads)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

基于手写数字识别的学习过程

import numpy as np
import matplotlib.pylab as plt
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label = True)

# x_train x_test 元素为0-1的数， n*1*784
# t_train t_test 元素为0或1 n*1*10

train_loss_list = [] #记录每次训练之后的损失函数
train_acc_list = [] #记录训练集精度
test_acc_list = [] #记录测试集精度

iters_num = 10000  # 梯度法的更新次数,10000次循环，每次取100个
train_size = x_train.shape[0] # 60000  训练数据一共60000个
batch_size = 100 # mini-batch选取，每次100个
learning_rate = 0.1 #学习率

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
iter_per_epoch = max(train_size / batch_size, 1) #训练600次可以将所有训练集覆盖一遍

for i in range(iters_num):
    # 获取mini-batch
    batch_mask = np.random.choice(train_size, batch_size) 
    #在60000个(train_size)中选100个(batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    

    # 计算梯度
    #grad = network.numerical_gradient(x_batch, t_batch)
    grad = network.gradient(x_batch, t_batch) # 高速版!
    
    # 更新参数
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]
    
     # 记录学习过程
    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)
    
    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))

x = np.arange(0,10000,1)
plt.plot(x, train_loss_list,label = 'loss')
plt.xlabel("训练次数")
plt.ylabel("loss")
plt.show()

x = np.arange(0,10000/600,1)
plt.plot(x,train_acc_list,label = 'train acc')
plt.plot(x,test_acc_list,label = 'test acc',linestyle = '--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0,1.0) #对y轴进行限制，0-1
plt.legend(loc = 'lower right') #创造图例
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

每一轮学习过后的精度变化

train acc, test acc | 0.12875, 0.1275
train acc, test acc | 0.76445, 0.7706
train acc, test acc | 0.87615, 0.8808
train acc, test acc | 0.89925, 0.9027
train acc, test acc | 0.9084833333333333, 0.911
train acc, test acc | 0.9151833333333333, 0.9173
train acc, test acc | 0.921, 0.9224
train acc, test acc | 0.9254166666666667, 0.926
train acc, test acc | 0.92875, 0.9286
train acc, test acc | 0.9328166666666666, 0.9327
train acc, test acc | 0.9352333333333334, 0.9354
train acc, test acc | 0.9376333333333333, 0.9364
train acc, test acc | 0.94, 0.9394
train acc, test acc | 0.9413833333333333, 0.9412
train acc, test acc | 0.9436666666666667, 0.9434
train acc, test acc | 0.9458166666666666, 0.9442
train acc, test acc | 0.94665, 0.9439
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

准确率变化图像

损失函数变化图像

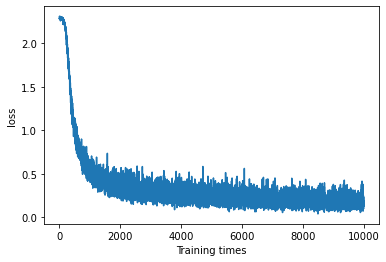
小结

​ 本章中，我们介绍了神经网络的学习。首先，为了能顺利进行神经网络 的学习，我们导入了损失函数这个指标。以这个损失函数为基准，找出使它的值达到最小的权重参数，就是神经网络学习的目标。为了找到尽可能小的 损失函数值，我们介绍了使用函数斜率的梯度法。