-
矩阵分析与应用+张贤达
第一章 矩阵与线性方程组(九)
1、两个随机向量的统计不相关与正交
- 当采样点 ξ ξ ξ取一系列值时,随机变量序列 x i ( ξ ) {x_i(ξ)} xi(ξ)构成一随机过程或信号
- 由于随机信号减去自己的均值后,只剩下随机变化部分,所以协方差函数给出的是两个随机信号 x i ( ξ ) x_i(ξ) xi(ξ)和 x j ( ξ ) x_j(ξ) xj(ξ)之间随机变化部分的相乘。
- 两个随机信号的随机变化部分中的共性部分的相乘总是取相同的符号,使得共性部分得到加强,而保留下来
- 两个信号的非共性部分则是随机的,它们的乘积有时取正,有时取负,通过数学期望的平均运算后,趋干相互抵消。
- 互协方差函数能够把两个信号之间随机变化的共性部分提取出来,并抑制掉非共性部分。
- 互协方差函数描述了两个信号
x
i
(
ξ
)
x_i(ξ)
xi(ξ)和
x
j
(
ξ
)
x_j(ξ)
xj(ξ)之间的相关(联)程度。即是说,互协方差函数越大,则这两个随机信号的相关程度越强;反之,相关程度越弱。但是,这种使用互协方差的绝对大小度量两个随机向量的相关程度并不方便。
两个随机变量 x ( ξ ) x(ξ) x(ξ)和 y ( ξ ) y(ξ) y(ξ)之间的相关系数定义为
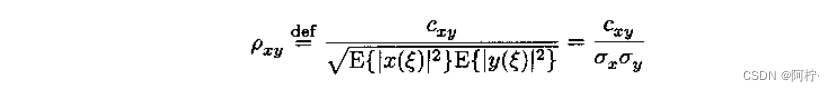
式中, c x y c_{xy} cxy是随机变量 x ( ξ ) x(ξ) x(ξ)和 y ( ξ ) y(ξ) y(ξ)之间的互协方差,而 σ x 2 σ_x^2 σx2和 σ y 2 σ_y^2 σy2分别是 x ( ξ ) x(ξ) x(ξ)和 y ( ξ ) y(ξ) y(ξ)的方差。对相关系数的定义公式使用Cauchy-Schwartz不等式,易知
0 ≤ ∣ P x y ∣ ≤ 1 0≤|P_{xy}|≤1 0≤∣Pxy∣≤1
相关系数 ρ x y \rho_{xy} ρxy给出了两个随机变量 x ( ξ ) x(ξ) x(ξ)和 y ( ξ ) y(ξ) y(ξ)之间的相似程度的度量: ρ x y \rho_{xy} ρxy越接近于零,随机变量 ρ x y \rho_{xy} ρxy的相似度越弱;
反之,若越接近于1,则 x ( ξ ) x(ξ) x(ξ)和 y ( ξ ) y(ξ) y(ξ)的相似度越大。
特别地,相关系数的两个极端值0和1有着重要的意义。
由于 ρ x y = 0 \rho_{xy}=0 ρxy=0意味着互协方差 C x y = 0 C_{xy}=0 Cxy=0,这表明随机变量 x ( ξ ) x(ξ) x(ξ)和 y ( ξ ) y(ξ) y(ξ)之间不存在任何相关部分。因此,若 ρ x y = 0 \rho_{xy}=0 ρxy=0,则称随机变量 x ( ξ ) x(ξ) x(ξ)和 y ( ξ ) y(ξ) y(ξ)不相关。
鉴丁这种不相关是在统计意义下定义的,所以常称之为统计不相关,以区别其他形式的不相关(如线性无关等)。-
若 x ( ξ ) = c y ( ξ ) x(ξ)=cy(ξ) x(ξ)=cy(ξ),其中, c c c为一复常数,则 ∣ ρ x y ∣ = 1 |\rho_{xy}|=1 ∣ρxy∣=1。
-
满足条件 x ( ξ ) = c y ( ξ ) = ∣ c ∣ e j ϕ ( c ) x(ξ)=cy(ξ)=|c|e^{j\phi(c)} x(ξ)=cy(ξ)=∣c∣ejϕ(c)的随机变量 x ( ξ ) x(ξ) x(ξ)和 y ( ξ ) y(ξ) y(ξ)只是相差一个固定的幅值比例因子和一个固定的相位 ϕ ( c ) \phi(c) ϕ(c)。这样的两个随机变量称为完全相关(或相干)。
-
将两个随机变量之间的不相关条件 c x y = 0 , i ≠ j c_{xy}=0,i≠j cxy=0,i=j推广到随机向量 x ( ξ ) x(ξ) x(ξ)和 y ( ξ ) y(ξ) y(ξ)的任意两个元素之间,则知当 c x i y j = 0 c_{x_iy_j}=0 cxiyj=0对所有 i , j i,j i,j恒成立时,随机向量 x ( ξ ) x(ξ) x(ξ)的任何元素都与随机向量 y ( ξ ) y(ξ) y(ξ)的任何元素不相关。此时,称随机变量 x ( ξ ) x(ξ) x(ξ)和 y ( ξ ) y(ξ) y(ξ)不相关。
随机向量的统计不相关定义为:
两个随机向量 x ( ξ ) x(ξ) x(ξ)和 y ( ξ ) y(ξ) y(ξ)统计不相关,若它们的互协方差矩阵等干零矩阵,即 C x y = 0 C_{xy}=0 Cxy=0。
两个随机变量 x ( ξ ) x(ξ) x(ξ)和 y ( ξ ) y(ξ) y(ξ)称为正交,若它们的互相关等于零,即
r x у = E x ( ξ ) y ∗ ( ξ ) = 0 r_{xу}=E{x(ξ)y^*(ξ)}=0 rxу=Ex(ξ)y∗(ξ)=0 -
类似地,两个随机向量 x ( ξ ) = [ x 1 ( ξ ) , x 2 ( ξ ) , … , x m ( ξ ) ] T x(ξ)=[x_1(ξ),x_2(ξ),…,x_m(ξ)]^T x(ξ)=[x1(ξ),x2(ξ),…,xm(ξ)]T和 y ( ξ ) = [ y 1 ( ξ ) , y 2 ( ξ ) , … , y n ( ξ ) ] T y(ξ)=[y_1(ξ),y_2(ξ),…,y_n(ξ)]^T y(ξ)=[y1(ξ),y2(ξ),…,yn(ξ)]T称为正交,若 x ( ξ ) x(ξ) x(ξ)的任一元素 x i ( ξ ) x_i(ξ) xi(ξ)与随机向量 y ( ξ ) y(ξ) y(ξ)的任意元素 y j ( ξ ) y_j(ξ) yj(ξ)正交,即 r x i y j = E x i ( ξ ) y j ( ξ ) = 0 , ∀ i , j r_{x_iy_j}= E{x_i(ξ)y_j(ξ)}=0,\forall i,j rxiyj=Exi(ξ)yj(ξ)=0,∀i,j。显然,这意味着这两个随机向量的互相关矩阵等于零矩阵,即有 R x y = O R_{xy}=O Rxy=O。
两个随机向量x(ξ)与y(ξ)正交:
若它们的互相关矩阵等于零矩阵,即 R x y = O R_{xy}=O Rxy=O。
2.随机向量的线性变换
令 A A A为一复常数矩阵,则
y ( ξ ) = A x ( ξ ) y(ξ)=Ax(ξ) y(ξ)=Ax(ξ)
是复正态随机向量 x ( ξ ) C N ( μ x , Г x ) x(ξ)~CN(μ_x,Г_x) x(ξ) CN(μx,Гx)的线性变换。
线性变换 y ( ξ ) = A x ( ξ ) y(ξ)=Ax(ξ) y(ξ)=Ax(ξ)仍然为正态随机向量,记作 y ( ξ ) C N ( μ y , Г y ) y(ξ)~CN(μ_y,Г_y) y(ξ) CN(μy,Гy)。容易验证,其均值向量
μ у = E y ( ξ ) = E A x ( ξ ) = A E x ( ξ ) = A μ x μ_у=E{y(ξ)} = E{Ax(ξ)} = AE{x(ξ)} = Aμ_x μу=Ey(ξ)=EAx(ξ)=AEx(ξ)=Aμx
自相关矩阵为
R y = E y ( ξ ) y H ( ξ ) = E A x ( ξ ) x H ( ξ ) A H R_y = E{y(ξ)y^H(ξ)} = E{ Ax(ξ)x^H(ξ)A^H} Ry=Ey(ξ)yH(ξ)=EAx(ξ)xH(ξ)AH
= A E x ( ξ ) x H ( ξ ) A H = A R x A H = AE{x(ξ)x^H(ξ)} A^H = AR_x A^H =AEx(ξ)xH(ξ)AH=ARxAH
自协方差矩阵为
C y = A C x A H C_y=AC_xA^H Cy=ACxAH
随机向量 x ( ξ ) x(ξ) x(ξ)与线性变换 y ( ξ ) = A x ( ξ ) y(ξ)=Ax(ξ) y(ξ)=Ax(ξ)的互相关矩阵为
R x y = E x ( ξ ) у H ( ξ ) = E x ( ξ ) x H ( ξ ) A H R_{xy} = E{x(ξ)у^H(ξ)} = E{x(ξ)x^H(ξ)A^H} Rxy=Ex(ξ)уH(ξ)=Ex(ξ)xH(ξ)AH
= E x ( ξ ) x H ( ξ ) A H = R x A H = E{x(ξ)x^H(ξ)} A^H = R_xA^H =Ex(ξ)xH(ξ)AH=RxAH
于是
R y x = R x y H = ( R x A H ) H = A R x R_{yx}=R_{xy}^H=(R_xA^H)^H=AR_x Ryx=RxyH=(RxAH)H=ARx
式中,利用了自协方差矩阵的共轭对称性 R x H = R x R_x^H=R_x RxH=Rx。
类似地,随机向量 x ( ξ ) x(ξ) x(ξ)与其线性变换 y ( ξ ) = A x ( ξ ) y(ξ)=Ax(ξ) y(ξ)=Ax(ξ)之间的互协方差矩阵
C x y = C x A H , C y x = A C x C_{xy}=C_xA^H,C_{yx}=AC_x Cxy=CxAH,Cyx=ACx -
相关阅读:
ASP.NET Core 6框架揭秘实例演示[35]:利用Session保留语境
P5143 攀爬者(快速排序)
TRC丨艾美捷 N,N-二甲基鸟嘌呤核苷说明书
【C语言】结构类型的定义和使用
【数据链路层】循环冗余码CRC、后退N帧协议GBN、选择重传协议SR、CSMA/CA
Redis分布式锁
量化日常工作指标
期中考misc复现
php如何解决高并发问题
cmake练习一
- 原文地址:https://blog.csdn.net/m0_45085885/article/details/125415910