-
深度学习损失函数 分类损失回归损失
损失函数是用于衡量模型所作出的预测离真实值(Ground Truth)之间的偏离程度。通常,我们都会最小化目标函数,最常用的算法便是“梯度下降法”(Gradient Descent)。损失函数大致可分为两种:回归损失(针对连续型变量)和分类损失(针对离散型变量)。
一、回归损失(Regression Loss)
L1 Loss(绝对值损失函数)
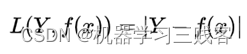
也称为Mean Absolute Error,即平均绝对误差(MAE),它衡量的是预测值与真实值之间距离的平均误差幅度,作用范围为0到正无穷。
优点: 对离群点(Outliers)或者异常值更具有鲁棒性。
缺点: 由图可知其在0点处的导数不连续,使得求解效率低下,导致收敛速度慢;而对于较小的损失值,其梯度也同其他区间损失值的梯度一样大,所以不利于网络的学习。
L2 Loss(平方损失)
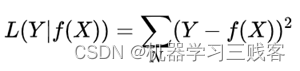
也称为Mean Squred Error,即均方差(MSE),它衡量的是预测值与真实值之间距离的平方和,作用范围同为0到正无穷。
优点:
(1)MSE损失函数是一个二次函数,并且值大于等于0。二次函数仅具有全局最小值。由于没有局部最小值,所以我们永远不会陷入它。因此,可以保证梯度下降将收敛到全局最小值(如果它完全收敛)。
(2)收敛速度快,能够对梯度给予合适的惩罚权重,而不是“一视同仁”,使梯度更新的方向可以更加精确。缺点:
(1) MSE损失函数通过平方误差来惩罚模型犯的大错误。一个比较大的数平方会使它变得更大。但有一点需要注意,这个属性使MSE成本函数对异常值十分敏感,梯度更新的方向很容易受离群点所主导,不具备鲁棒性。因此,如果我们的数据容易出现许多的异常值,则不应使用这个它。
(2)具体到深度学习领域,MSE 的缺陷在于,当它和 Sigmoid 激活函数一起出现时,可能会出现学习速度缓慢(收敛变慢)的情况。对于L1范数和L2范数,如果异常值对于实际业务非常重要,我们可以使用MSE作为我们的损失函数;另一方面,如果异常值仅仅表示损坏的数据,那我们应该选择MAE作为损失函数。此外,考虑到收敛速度,在大多数的卷积神经网络中(CNN)中,我们通常会选择L2损失。但是,还存在这样一种情形,当你的业务数据中,存在95%的数据其真实值为1000,而剩下5%的数据其真实值为10时,如果你使用MAE去训练模型,则训练出来的模型会偏向于将所有输入数据预测成1000,因为MAE对离群点不敏感,趋向于取中值。而采用MSE去训练模型时,训练出来的模型会偏向于将大多数的输入数据预测成10,因为它对离群点异常敏感。因此,大多数情况这两种回归损失函数并不适用,能否有什么办法可以同时利用这两者的优点呢?
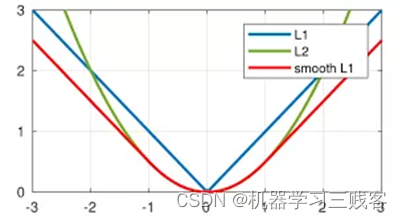
Smooth L1 Loss——平滑的L1损失(Huber损失)
即平滑的L1损失(SLL),出自Fast RCNN[2]。平滑的L1损失(SLL)通过综合L1和L2损失的优点,在0点处附近采用了L2损失中的平方函数,解决了L1损失在0点处梯度不可导的问题,使其更加平滑易于收敛。平滑的L1损失相比于平方损失来说对于局外点不敏感,但它同样保持了可微的特性。它基于绝对误差但在误差很小的时候变成了平方误差。我们可以使用超参数δ来调节这一误差的阈值。当δ趋向于0时它就退化成了MAE,而当δ趋向于无穷时则退化为了MSE,其表达式如下,是一个连续可微的分段函数:
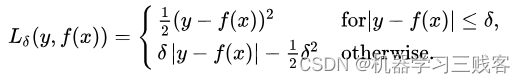
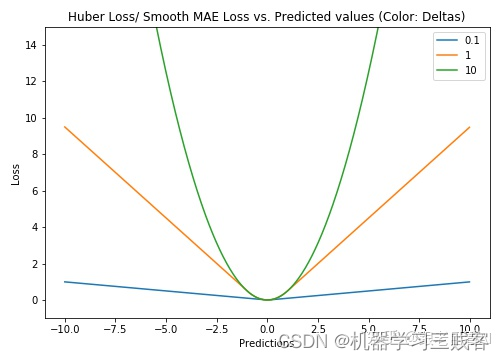
特点:
(1)对于SLL来说,δ的选择十分重要,它决定了模型处理局外点的行为。当残差大于δ时使用L1损失,很小时则使用更为合适的L2损失来进行优化。
(2)SLL损失函数克服了MAE和MSE的缺点,不仅可以保持损失函数具有连续的导数,同时可以利用MSE梯度随误差减小的特性来得到更精确的最小值,也对局外点具有更好的鲁棒性。
(3)但SSL损失函数的良好表现得益于精心训练的超参数δ。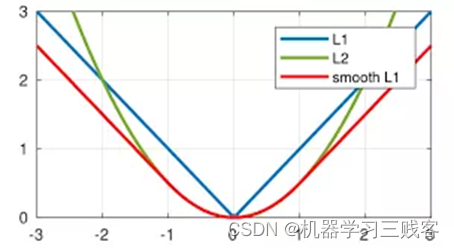
通过对这三个损失函数进行求导可以发现,L1损失的导数为常数,如果不及时调整学习率,那么当值过小时,会导致模型很难收敛到一个较高的精度,而是趋向于一个固定值附近波动。反过来,对于L2损失来说,由于在训练初期值较大时,其导数值也会相应较大,导致训练不稳定。最后,可以发现Smooth L1在训练初期输入数值较大时能够较为稳定在某一个数值,而在后期趋向于收敛时也能够加速梯度的回传,很好的解决了前面两者所存在的问题。
IoU Loss
即交并比损失,出自UnitBox[3],由旷视科技于ACM2016首次提出。常规的
Lx损失中,都是基于目标边界中的4个坐标点信息之间分别进行回归损失计算的。因此,这些边框信息之间是相互独立的。然而,直观上来看,这些边框信息之间必然是存在某种相关性的。如下图(a)-(b)分别所示,绿色框代表Ground Truth,蓝色框代表Prediction,可以看出,同一个Lx分数,预测框与真实框之间的拟合/重叠程度并不相同,显然重叠度越高的预测框是越合理的。IoU损失将候选框的四个边界信息作为一个整体进行回归,从而实现准确、高效的定位,具有很好的尺度不变性。为了解决IoU度量不可导的现象,引入了负Ln范数来间接计算IoU损失。

GIoU Loss
即泛化的IoU损失,全称为Generalized Intersection over Union,由斯坦福学者于CVPR2019年发表的这篇论文[4]中首次提出。上面我们提到了IoU损失可以解决边界框坐标之间相互独立的问题,考虑这样一种情况,当预测框与真实框之间没有任何重叠时,两个边框的交集(分子)为0,此时IoU损失为0,因此IoU无法算出两者之间的距离(重叠度)。另一方面,由于IoU损失为零,意味着梯度无法有效地反向传播和更新,即出现梯度消失的现象,致使网络无法给出一个优化的方向。此外,如下图所示,IoU对不同方向的边框对齐也是一脸懵逼的,所计算出来的值都一样。

图2.两个具有完全相同IoU值的矩形之间的三种不同重叠方式,即IoU=0.33,但不同的IoU值,即从左到右GIoU=0.33、0.24和-0.1。对于对齐方向更好的情况,GIoU值将更高。
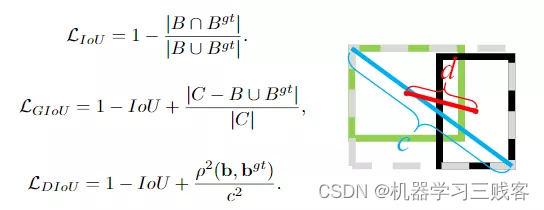
为了解决以上的问题,如下图公式所示,GIoU通过计算任意两个形状(这里以矩形框为例)A和B的一个最小闭合凸面C,然后再计算C中排除掉A和B后的面积占C原始面积的比值,最后再用原始的IoU减去这个比值得到泛化后的IoU值。

GIoU具有IoU所拥有的一切特性,如对称性,三角不等式等。GIoU ≤ IoU,特别地,0 ≤ IoU(A, B) ≤ 1, 而-1 ≤ GIoU(A, B) ≤ 1;当两个边框的完全重叠时,此时GIoU = IoU = 1. 而当 |AUB| 与 最小闭合凸面C 的比值趋近为0时,即两个边框不相交的情况下,此时GIoU将渐渐收敛至 -1. 同样地,我们也可以通过一定的方式去计算出两个矩形框之间的GIoU损失,具体计算步骤也非常简单,详情参考原论文。
DIoU Loss
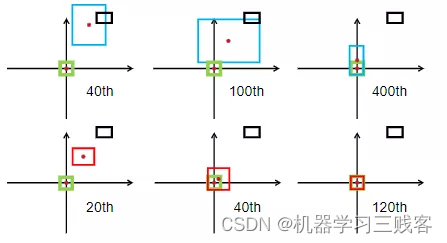
即距离IoU损失,全称为Distance-IoU loss,由天津大学数学学院研究人员于AAAI2020所发表的这篇论文[5]中首次提出。上面我们谈到GIoU通过引入最小闭合凸面来解决IoU无法对不重叠边框的优化问题。但是,其仍然存在两大局限性:边框回归还不够精确 & 收敛速度缓慢。考虑下图这种情况,当目标框完全包含预测框时,此时GIoU退化为IoU。显然,我们希望的预测是最右边这种情况。因此,作者通过计算两个边框之间的中心点归一化距离,从而更好的优化这种情况。

下图表示的是GIoU损失(第一行)和DIoU损失(第二行)的一个训练过程收敛情况。其中绿色框为目标边框,黑色框为锚框,蓝色框和红色框则分别表示使用GIoU损失和DIoU损失所得到的预测框。可以发现,GIoU损失一般会增加预测框的大小使其能和目标框重叠,而DIoU损失则直接使目标框和预测框之间的中心点归一化距离最小,即让预测框的中心快速的向目标中心收敛。
图左给出这三个IoU损失所对应的计算公式。对于DIoU来说,如图右所示,其惩罚项由两部分构成:分子为目标框和预测框中心点之间的欧式距离;分母为两个框最小外接矩形框的两个对角线距离。因此, 直接优化两个点之间的距离会使得模型收敛得更快,同时又能够在两个边框不重叠的情况下给出一个优化的方向。
CIoU Loss
即完整IoU损失,全称为Complete IoU loss,与DIoU出自同一篇论文。上面我们提到GIoU存在两个缺陷,DIoU的提出解决了其实一个缺陷,即收敛速度的问题。而一个好的边框回归损失应该同时考虑三个重要的几何因素,即重叠面积(Overlap area)、中心点距离(Central point distance)和高宽比(Aspect ratio)。GIoU考虑到了重叠面积的问题,DIoU考虑到了重叠面积和中心点距离的问题,CIoU则在此基础上进一步的考虑到了高宽比的问题。 CIoU的计算公式如下所示,可以看出,其在DIoU的基础上加多了一个惩罚项αv。其中α为权重为正数的重叠面积平衡因子,在回归中被赋与更高的优先级,特别是在两个边框不重叠的情况下;而v则用于测量宽高比的一致性。

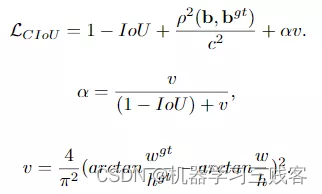
F-EIoU Loss
《Focal and Efficient IoU Loss》[6]是由华南理工大学学者最近提出的一篇关于目标检测损失函数的论文,文章主要的贡献是提升网络收敛速度和目标定位精度。目前检测任务的损失函数主要有两个缺点:(1)无法有效地描述边界框回归的目标,导致收敛速度慢以及回归结果不准确(2)忽略了边界框回归中不平衡的问题。
F-EIou loss首先提出了一种有效的交并集(IOU)损失,它可以准确地测量边界框回归中的重叠面积、中心点和边长三个几何因素的差异:
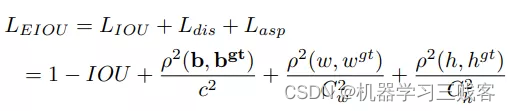
其次,基于对有效样本挖掘问题(EEM)的探讨,提出了Focal loss的回归版本,以使回归过程中专注于高质量的锚框:
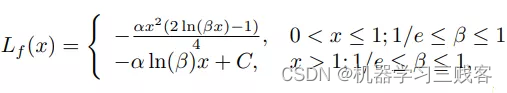
最后,将以上两个部分结合起来得到Focal-EIou Loss:
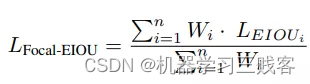
其中,通过加入每个batch的权重和来避免网络在早期训练阶段收敛慢的问题。
CDIoU Loss
《Control Distance IoU Loss》[7]是由同济大学学者提出的,文章的主要贡献是在几乎不增强计算量的前提下有效提升了边界框回归的精准度。目前检测领域主要两大问题:(1)SOTA算法虽然有效但计算成本高(2)边界框回归损失函数设计不够合理。
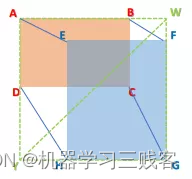
文章首先提出了一种对于Region Propasl(RP)和Ground Truth(GT)之间的新评估方式,即CDIoU。可以发现,它虽然没有直接中心点距离和长宽比,但最终的计算结果是有反应出RP和GT的差异。计算公式如下:

对比以往直接计算中心点距离或是形状相似性的损失函数,CDIoU能更合理地评估RP和GT的差异并且有效地降低计算成本。然后,根据上述的公式,CDIoU Loss可以定义为:
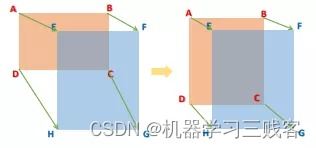
通过观察这个公式,可以直观地感受到,在权重迭代过程中,模型不断地将RP的四个顶点拉向GT的四个顶点,直到它们重叠为止,如下图所示。
二、分类损失
0-1损失函数(zero-one loss)
0-1损失是指预测值和目标值不相等为1, 否则为0:特点:
(1)0-1损失函数直接对应分类判断错误的个数,但是它是一个非凸函数,不太适用.
(2) 感知机就是用的这种损失函数。但是相等这个条件太过严格,因此可以放宽条件,即满足 时认为相等,指数损失函数(exponential loss)
指数损失函数的标准形式如下:特点:
(1) 对离群点、噪声非常敏感。经常用在AdaBoost算法中。
学过Adaboost算法的人都知道,它是前向分步加法算法的特例,是一个加和模型,损失函数就是指数函数。在Adaboost中,经过m此迭代之后,可以得到fm(x):Adaboost每次迭代时的目的是为了找到最小化下列式子时的参数α 和G:
Hinge 损失函数
Hinge损失函数标准形式如下:特点:
(1)hinge损失函数表示如果被分类正确,损失为0,否则损失就为 。SVM就是使用这个损失函数。
(2)一般的f(x) 是预测值,在-1到1之间, y 是目标值(-1或1)。其含义是, f(x)的值在-1和+1之间就可以了,并不鼓励|f(x)|>1 ,即并不鼓励分类器过度自信,让某个正确分类的样本距离分割线超过1并不会有任何奖励,从而使分类器可以更专注于整体的误差。(2) 健壮性相对较高,对异常点、噪声不敏感,但它没太好的概率解释。
感知损失(perceptron loss)函数
感知损失函数的标准形式如下:特点:
(1) 是Hinge损失函数的一个变种,Hinge loss对判定边界附近的点(正确端)惩罚力度很高。而perceptron loss只要样本的判定类别正确的话,它就满意,不管其判定边界的距离。它比Hinge loss简单,因为不是max-margin boundary,所以模型的泛化能力没 hinge loss强。交叉熵损失函数 (Cross-entropy loss function)
交叉熵损失函数的标准形式如下:注意公式中 x 表示样本,y表示实际的标签,a表示预测的输出, n表示样本总数量。
特点:
(1)本质上也是一种对数似然函数,可用于二分类和多分类任务中。
二分类问题中的loss函数(输入数据是softmax或者sigmoid函数的输出):多分类问题中的loss函数(输入数据是softmax或者sigmoid函数的输出):
(2) 当使用sigmoid作为激活函数的时候,常用交叉熵损失函数而不用均方误差损失函数,因为它可以完美解决平方损失函数权重更新过慢的问题,具有“误差大的时候,权重更新快;误差小的时候,权重更新慢”的良好性质。
K-L Divergence
即KL散度。对于交叉熵损失,除了我们在这里使用预测概率的对数(log(q(i)))外,它看起来与上面熵的方程非常相似。如果我们的预测是完美的,那就是预测分布等于真实分布,此时交叉熵就等于熵。但是,如果分布不同,则交叉熵将比熵大一些位数。交叉熵超过熵的量称为相对熵,或更普遍地称为KL散度。总结如下:
、(1)KL散度是发散函数,不对称,所以不能作为距离度量
(2)与多分类分类相比,KL散度更常用于逼近复杂函数。我们在使用变分自动编码器(VAE)等深度生成模型时经常使用KL散度。Dice Loss
即骰子损失,出自V-Net [3],是一种用于评估两个样本之间相似性度量的函数,取值范围为0~1,值越大表示两个值的相似度越高,其基本定义(二分类)如下:其中,|X∩Y|表示X和Y之间的交集,|X|和|Y|分别表示集合X和Y中像素点的个数,分子乘于2保证域值范围在0~1之间,因为分母相加时会计算多一次重叠区间,如下图:
从右边公式也可以看出,其实Dice系数是等价于F1分数的,优化Dice等价于优化F1值。此外,为了防止分母项为0,一般我们会在分子和分母处同时加入一个很小的数作为平滑系数,也称为拉普拉斯平滑项。Dice损失由以下两个主要特性:
• 有益于正负样本不均衡的情况,侧重于对前景的挖掘;(前景:目标事物,正类 背景:背景图,负类)
• 训练过程中,在有较多小目标的情况下容易出现振荡;
• 极端情况下会出现梯度饱和的情况。
所以一般来说,我们都会结合交叉熵损失或者其他分类损失一同进行优化。Focal Loss
焦点损失,出自何凯明的《Focal Loss for Dense Object Detection》[9],出发点是解决目标检测领域中one-stage算法如YOLO系列算法准确率不高的问题。作者认为样本的类别不均衡(比如前景和背景)是导致这个问题的主要原因。比如在很多输入图片中,我们利用网格去划分小窗口,大多数的窗口是不包含目标的。如此一来,如果我们直接运用原始的交叉熵损失,那么负样本所占比例会非常大,主导梯度的优化方向,即网络会偏向于将前景预测为背景。即使我们可以使用OHEM(在线困难样本挖掘)算法来处理不均衡的问题,虽然其增加了误分类样本的权重,但也容易忽略掉易分类样本。而Focal loss则是聚焦于训练一个困难样本的稀疏集,通过直接在标准的交叉熵损失基础上做改进,引进了两个惩罚因子,来减少易分类样本的权重,使得模型在训练过程中更专注于困难样本。其基本定义如下:
其中:
• 参数α和(1-α)分别用于控制正/负样本的比例,其取值范围为[0, 1]。α的取值一般可通过交叉验证来选择合适的值。
• 参数γ称为聚焦参数,其取值范围为[0, +∞),目的是通过减少易分类样本的权重,从而使模型在训练时更专注于困难样本。 当 γ = 0 时,Focal Loss就退化为交叉熵损失,γ 越大,对易分类样本的惩罚力度就越大。
实验中,作者取(α=0.25,γ=0.2)的效果最好,具体还需要根据任务的情况调整。由此可见,应用Focal-loss也会引入多了两个超参数需要调整,而一般来说很需要经验才能调好。Contrastive Loss
对比损失函数,来自Yann LeCun的论文Dimensionality Reduction by Learning an Invariant Mapping,出发点想让增大类间差异并且减小类内差异.
公式如下:其中 d=||an−bn||2,代表两个样本特征的欧氏距离,y为两个样本是否匹配的标签,y=1代表两个样本相似或者匹配,y=0则代表不匹配,margin为设定的阈值。
使用场景:主要是用在降维中,即本来相似的样本,在经过降维(特征提取)后,在特征空间中,两个样本仍旧相似;而原本不相似的样本,在经过降维后,在特征空间中,两个样本仍旧不相似。
观察上述的contrastive loss的表达式可以发现,这种损失函数可以很好的表达成对样本的匹配程度,也能够很好用于训练提取特征的模型。当y=1(即样本相似)时,损失函数只剩下∑yd2,即原本相似的样本,如果在特征空间的欧式距离较大,则说明当前的模型不好,因此加大损失。而当y=0时(即样本不相似)时,损失函数为∑(1−y)max(margin−d,0)2,即当样本不相似时,其特征空间的欧式距离反而小的话,损失值会变大,这也正好符号我们的要求。
这张图表示的就是损失函数值与样本特征的欧式距离之间的关系,其中红色虚线表示的是相似样本的损失值,蓝色实线表示的不相似样本的损失值。
Triplet Loss
来自论文FaceNet: A Unified Embedding for Face Recognition and Clustering,三元组损失是一种被广泛使用的度量学习损失,之后的大量度量学习方法也是基于三元组损失演变而来的。顾名思义,三元组损失就是需要三张图片作为输入。和对比损失不同,一个输入的三元组(Triplet)包括一个正样本对和一个负样本对,三张图片分别命名为固定图片(Anchor)a、正样本图片(Positive)p和负样本图片(Negative)n,则三元组损失表示为:如下图所示,三元组损失可以拉近正样本对之间的距离,推开负样本对之间的距离,最后使得相同ID的行人图片在特征空间里形成聚类,达到行人重识别目的:
特点:
(1)可以学到较好的人脸的embedding。属于多分类问题。
(2)不使用softmax,因为softmax最终的类别数是确定的。
(3)缺点:类内方差没有考虑,只考虑了类间。鲁棒性不强适用场景:人脸识别 个体级别的细粒度识别
Center Loss
中心损失函数center loss,来自论文A Discriminative Feature Learning Approach for Deep Face Recognition,其目的是关注类内分布均匀性的,想让其绕类内中心均匀分布,最小化类内差异,它仅仅用来减少类内(比如说同一表情)的差异,而不能有效增大类间(比如说不同表情)的差异性,公式如下:c表示第yi个类别的特征中心,xi表示全连接层之前的特征。N表示mini-batch的大小
这个公式就是希望一个batch中的每个样本的feature离feature的中心的距离的平方和要越小越好,也就是类内距离要越小越好。这就是center loss.适用场景:人脸表情识别
References
[2]
https://arxiv.org/abs/1504.08083
[3]
https://arxiv.org/abs/1608.01471
[4]
https://arxiv.org/abs/1902.09630
[5]
https://arxiv.org/abs/1911.08287
[6]
https://arxiv.org/abs/2101.08158
[7]
https://arxiv.org/abs/2103.11696
[8]
https://towardsdatascience.com/entropy-cross-entropy-and-kl-divergence-explained-b09cdae917a
[9]
https://arxiv.org/abs/1708.02002 -
相关阅读:
SpringBoot 08 MVC扩展配置的原理
十进制小数转换为单双精度浮点数方法
MySQL高阶语句(一)
短视频不知道怎么定位?教你三个自我商业定位的方法,收藏学习
MapReduce理论
【函数式编程实战】(九) Optional实战大全
【入门】.Net Core 6 WebApi 项目搭建
给 Ubuntu 操作系统配置静态 IP
第28讲:Ceph集群使用RBD块存储与K8S Volumes集成
Linux基础(四)
- 原文地址:https://blog.csdn.net/qq_42121640/article/details/125416679