-
Mip-NeRF:抗混叠的多尺度神经辐射场ICCV2021

混叠现象
数据采集时,如果采样频率不满足奈奎斯特采样定理,可能会导致采样后的信号存在混叠。
当采样频率设置不合理时,即采样频率低于2倍的信号频率时,会导致原本的高频信号被采样成低频信号。如下图所示,红色信号是原始的高频信号,但是由于采样频率不满足采样定理的要求,导致实际采样点如图中蓝色实心点所示,将这些蓝色实际采样点连成曲线,可以明显地看出这是一个低频信号。
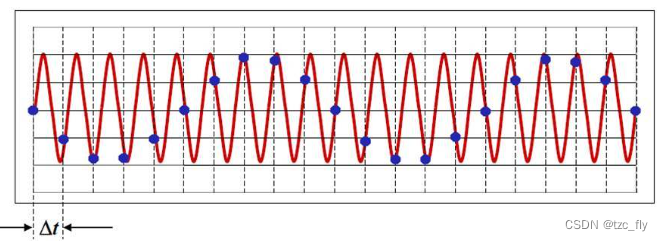
对连续信号进行等时间采样时,如果采样频率不满足采样定理,采样后的信号频率就会发生混叠,也就是高频信号被混叠成了低频信号。对于图像,图像的高频信息即灰度变化陡峭的部分,图像中的混叠部分即高频内容被表现为低频内容,也就是我们所说的模糊现象(近距离观察),以及锯齿状的边缘外观(远距离观察)。
NeRF只在相机到对象距离固定的情况下可以生成表现优秀的结果,当相机拉近,拉远场景时会产生模糊和锯齿。产生的原因是采样频率低于真实原始信号的频率,为了解决这一问题,我们可以:提高采样率或者粗暴去除高频分量(使用低通滤波器对边缘进行平滑)。

- NeRF(左)存在近距离模糊和远距离锯齿现象,Mip-NeRF(右)
NeRF对每一个像素只发射一条光线,如果发射多条光线,提高了采样率,一定程度上可以解决模糊和锯齿问题,但这样的方法大大增加了计算量,效率太低,为此,mip-nerf提出使用圆锥体取代光线的方案。
Mip-NeRF概述
mip来源于拉丁语(放置很多东西的小空间),在计算机图形学中,mipmapping是一种加速渲染,减少图像锯齿的技术。简单说,mipmapping就是把主图缩小成一系列依次缩小的图片,并把这些更低分辨率的小图片保存起来。这种策略被称为pre-filtering,抗锯齿的计算负担都集中在预处理上:不论之后需要对一个texture做多少次渲染,都只需要基于第一次的预处理即可。
Mip-NeRF提出的背景是:在渲染过程中,如果NeRF在每个pixel用single ray来sample场景,(NeRF在做渲染时)会出现模糊(blurred)和锯齿(aliased)的情况,这种情况通常是由于同一个场景对应的多个图片的分辨率(resolution)不一致而导致的(由于相机距离不同,导致相对的采样频率改变,从而引起信号失真)。最简明的解决方法是渲染时,对每个pixel用multiple rays。但是对NeRF来说并不现实,因为沿着一条ray渲染就需要query一个MLP几百次。
Mip-NeRF的解决方案和NeRF有一个本质不同:NeRF渲染是要基于ray的,然而Mip-NeRF是基于conical frustums(圆锥)的,并且是anti-aliased(抗混叠)的。最终,Mip-NeRF与NeRF相比具有更快、更小、更准的优势,更加适合处理multiscale的数据。
位置编码IPE
经典的位置编码(用于Transformer和神经辐射场)将空间中的单个点映射到特征向量,向量中的每个元素由频率呈指数增长的正弦曲线生成: γ w ( x ) = s i n ( w x ) , γ ( x ) = [ γ 2 l ( x ) ] l = 0 L − 1 \gamma_{w}(x)=sin(wx),\gamma(x)=[\gamma_{2^{l}}(x)]_{l=0}^{L-1} γw(x)=sin(wx),γ(x)=[γ2l(x)]l=0L−1这里,我们展示了这些特征向量是如何随一维空间中的点的移动而变化的(令 L = 5 L=5 L=5):
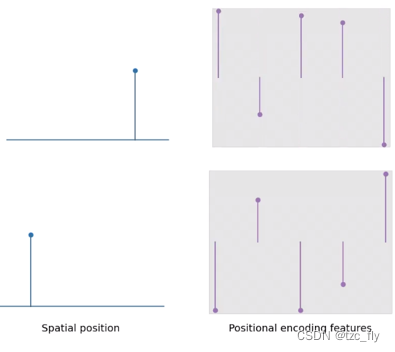
mip-nerf的 integrated positional encoding 考虑空间中的 Gaussian regions,而不是无穷小的一个点。这提供了一种自然的方式,可以将空间的“region”作为query输入到基于coordinate的神经网络。每个位置编码的期望值有一个简单的形式: E x ∼ N ( μ , σ 2 ) [ γ w ( x ) ] = s i n ( w μ ) e x p ( − ( w σ ) 2 / 2 ) E_{x\sim N(\mu,\sigma^{2})}[\gamma_{w}(x)]=sin(w\mu)exp(-(w\sigma)^{2}/2) Ex∼N(μ,σ2)[γw(x)]=sin(wμ)exp(−(wσ)2/2)我们可以看到,当考虑更宽阔的region时(远景),高频信息会自动收缩到零,从而为网络提供更多低频信息。随着region缩小(近景),这些位置特征信号会接近经典位置编码。
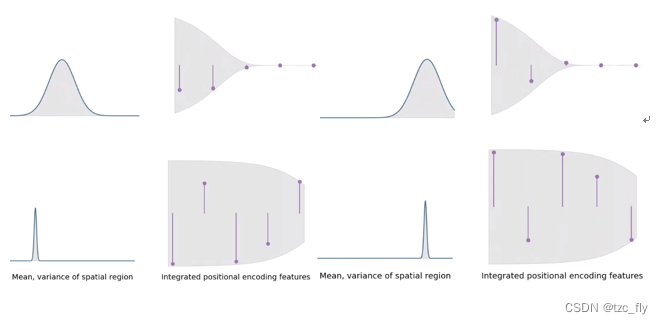
这种动态的设置,使得nerf处理远景自动过滤高频信息,缓解了锯齿现象(即去除了景象中的高频分量),处理近景时恢复对高频信息的处理。Mip-NeRF
使用IPE来训练NeRF以生成抗锯齿的渲染。mip-nerf不是通过每个像素投射一条宽度无限小的光线,而是投射一个完整的3D圆锥体。对于沿射线的每个查询点,我们考虑其关联的圆锥截锥体。两个不同位置的相机观察空间中的同一点可能会产生截然不同的圆锥截锥体,如下图所示:
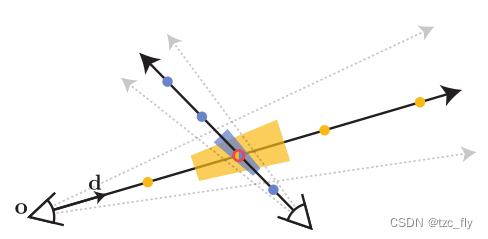
我们将多元高斯拟合到圆锥截锥体,并使用上述IPE创建MLP网络的输入特征向量。
直观看,使用锥体渲染的好处在于:锥体反映了场景中某个点的形状和大小,因为不同视角下,某个点的形状和大小不同,即圆锥截锥体(上图中的梯形)的大小和形状也不同。反映到计算上就是不同位置的相机,对于同一个观测点的位置编码的期望值不同。
Introduction
神经辐射场(NeRF)已成为一种引人注目的策略,用于从图像中学习表示3D对象和场景,以渲染照片级真实感的新视图。尽管NeRF及其变体在一系列视图合成任务中取得了令人印象深刻的结果,但NeRF渲染模型存在缺陷,可能会导致过度模糊(近景)和锯齿(远景)。NeRF将传统的离散采样替换为连续的体积函数,将其参数化为多层感知器(MLP),该感知器从输入的5D坐标(3D位置和2D观察方向)映射到该位置的场景属性(体积密度和由视角而定的发射辐射度)。若要渲染像素的颜色,NeRF将通过该像素投射一条光线,并将其输出到其体积表示中,沿着该光线采样查询MLP获取场景属性,将这些值合成为单一颜色。
虽然当所有训练和测试图像仅从大致恒定的距离观察场景内容时,这种方法效果很好(就像在NeRF和大多数后续工作中所做的那样),但NeRF渲染在不太人为的场景中显示出明显的瑕疵。当训练图像以多个分辨率观察场景内容时,恢复的NeRF的渲染在特写视图(近距离观察情况)中显得过于模糊,在远视图(远距离观察)中包含锯齿。一个简单的解决方案是采用离线光线跟踪中使用的策略:通过将多条光线推进其足迹来对每个像素进行超采样。但对于神经体积表示法(如NeRF)来说,这种方法代价高昂,因为渲染一条光线就需要查询MLP数百次,最终需要几个小时才能重建一个场景。
在本文中,我们从用于防止计算机图形渲染管道中出现混叠的mipmapping方法中得到了启发。mipmap其实就是一个多分辨率的图像金字塔结构。
我们的解决方案称为mip-NeRF(multum in parvo-NeRF,如“mipmap”)。mip-NeRF的输入是一个三维高斯分布,表示辐射场应在其上积分的region。如图1所示,然后我们可以通过沿圆锥体每隔一段距离查询mip-NeRF,使用近似于该像素对应的圆锥形截锥体的高斯分布来渲染像素。为了对3D位置及其周围的Gaussian region进行编码,我们提出了一种新的特征表示:集成位置编码(IPE,integrated positional encoding)。这是NeRF的位置编码(PE)的推广,它允许空间region被紧凑地特征化,而不是空间中的单个点。
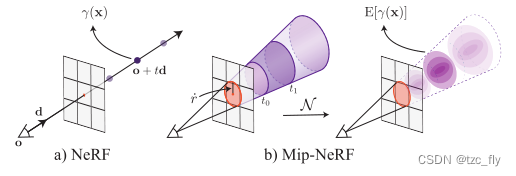
- 图1:NeRF(a)沿着从相机投影中心通过像素跟踪的光线对点 x \textbf{x} x进行采样, d \textbf{d} d是观察方向,然后使用位置编码PE γ γ γ对这些点进行编码,以生成特征 γ ( x ) γ(\textbf{x}) γ(x)。Mip-NeRF(b)转而解释为相机像素定义的三维圆锥形截锥。然后,使用我们的集成位置编码(IPE)对这些圆锥形截锥体进行特征化,IPE的工作原理是用多元高斯近似截锥体,然后计算高斯坐标位置编码上的积分 E [ γ ( x ) ] E[γ(\textbf{x})] E[γ(x)]。
Mip-NeRF大大提高了NeRF的准确性。在我们提出的一个具有挑战性的多分辨率基准上,mip-NeRF相对于NeRF能够平均降低60%的错误率。Mip-NeRF的尺度感知结构还允许我们将NeRF用于分层采样的"coarse"和"fine"MLP合并到单个MLP中。因此,mip-NeRF略快于NeRF,并且具有一半的参数。
Method
当使用圆锥体替换光线后,采样的不再是离散的点集,而是一个连续的圆锥截台(conical frustum),这能够解决NeRF中忽略了光线观察范围体积与大小的问题。
为了计算的简便,我们使用3D Gaussian来近似 conical frustum(圆锥截台),并提出使用IPE代替PE。IPE被定义为高斯分布的positional encoding的期望值。
Gaussian分布的优点很多,其中之一便是线性变换。将positional encoding改写为矩阵形式后,输入高斯分布进行运算,等价于对高斯分布的均值与协方差进行变换。
首先,PE的矩阵形式为:
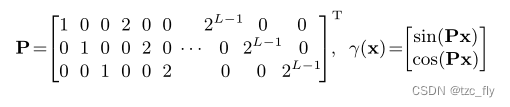
注意, x \textbf{x} x是空间位置, d \textbf{d} d是观察方向,我们定义 μ t \mu_{t} μt为采样点 t t t对应的圆锥截体到相机的平均距离(沿着光线的平均距离),另外, σ t 2 \sigma_{t}^{2} σt2为沿着光线的距离方差, σ r 2 \sigma_{r}^{2} σr2为垂直于光线的距离方差。我们可以得到采样点 t t t对应的圆锥截锥体的高斯分布: u = o + μ t d \textbf{u}=\textbf{o}+\mu_{t}\textbf{d} u=o+μtd Σ = σ t 2 ( d d T ) + σ r 2 ( I − d d T ∣ ∣ d ∣ ∣ 2 2 ) \Sigma=\sigma_{t}^{2}(\textbf{d}\textbf{d}^{T})+\sigma_{r}^{2}(\textbf{I}-\frac{\textbf{d}\textbf{d}^{T}}{||\textbf{d}||_{2}^{2}}) Σ=σt2(ddT)+σr2(I−∣∣d∣∣22ddT)我们对高斯分布进行位置编码,位置编码必然服从高斯分布,且均值和方差为: u γ = Pu \textbf{u}_{\gamma}=\textbf{P}\textbf{u} uγ=Pu Σ γ = P Σ P T \Sigma_{\gamma}=\textbf{P}\Sigma\textbf{P}^{T} Σγ=PΣPT根据这个高斯分布,我们可以获得IPE: γ ( u , Σ ) = E x ∼ N ( u γ , Σ γ ) [ γ ( x ) ] \gamma(\textbf{u},\Sigma)=E_{\textbf{x}\sim N(\textbf{u}_{\gamma},\Sigma_{\gamma})}[\gamma(\textbf{x})] γ(u,Σ)=Ex∼N(uγ,Σγ)[γ(x)] = [ sin ( u γ ) ∘ e x p ( − ( 1 2 ) d i a g ( Σ γ ) ) , cos ( u γ ) ∘ e x p ( − ( 1 2 ) d i a g ( Σ γ ) ) ] T =[\text{sin}(\textbf{u}_{\gamma})\circ exp(-(\frac{1}{2})diag(\Sigma_{\gamma})),\text{cos}(\textbf{u}_{\gamma})\circ exp(-(\frac{1}{2})diag(\Sigma_{\gamma}))]^{T} =[sin(uγ)∘exp(−(21)diag(Σγ)),cos(uγ)∘exp(−(21)diag(Σγ))]T d i a g ( Σ γ ) = [ d i a g ( Σ ) , 4 d i a g ( Σ ) , . . . , 4 L − 1 d i a g ( Σ ) ] T diag(\Sigma_{\gamma})=[diag(\Sigma),4diag(\Sigma),...,4^{L-1}diag(\Sigma)]^{T} diag(Σγ)=[diag(Σ),4diag(Σ),...,4L−1diag(Σ)]T其中, ∘ \circ ∘为element-wise乘积。 d i a g diag diag为取矩阵的对角线。mip-nerf利用截锥体采样,考虑了不同尺度的信息,因此只需要学习一个MLP就能表示粗粒度和细粒度信息。
讨论
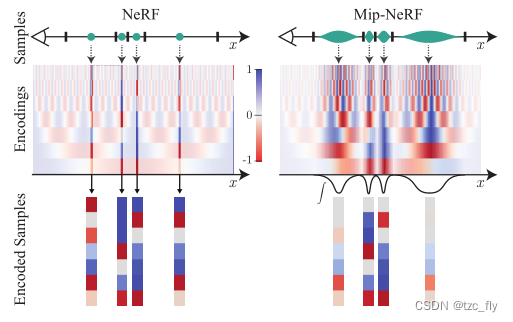
- 图2:NeRF使用的位置编码 PE(左)和mip-nerf集成位置编码 IPE(右)。由于NeRF沿每条光线采样,并对所有频率进行编码,对于那些高频特征(超过采样频率)总会导致渲染出现混叠。通过在每个间隔上集成PE特征,当采样频率周期与IPE的间隔大小相比较小时,IPE特征的高频维度向零收缩,避免混叠现象。
上图可视化了IPE和PE的一维特征之间的差异。IPE特征的行为是直观的:如果位置编码中的频率周期小于构造IPE特征的间隔宽度(在这种情况下,该间隔上的PE将重复振荡),则该频率下的特征将缩小到0。IPE特征是有效的抗混叠位置编码,可以柔和地编码空间体积的大小和形状。
IPE每次采样都能确保相对于IPE特征间隔的高频特征被弱化,因为每个圆锥截锥体的高斯分布总是跟随IPE特征间隔动态变化的
Mip-NeRF最主要的贡献在于改进了采样方式,使用圆锥截锥体代替光线中的一个点,为了计算方便,提出服从三维高斯分布的region近似圆锥截锥体,根据高斯分布的特性,得到位置编码对应的高斯分布,从这个高斯分布采样位置编码,并计算期望作为最后的位置编码。
服从高斯分布的位置编码可以自动在采样频率较低时(IPE特征间隔较宽时)弱化高频特征,从而缓解混叠现象。这种采样设计本身决定了其适用于多尺度情况,因此,Nerf的两个MLP可以合并为一个MLP。
-
相关阅读:
【技术积累】JavaScript中的函数【一】
毕业设计-基于SpringBoot校园论坛管理系统
2311rust过程宏的示例
GitHub 和 GitLab 同时管理
云计算学习笔记——第三章 计算虚拟化[二]
AtCoder ABC001C 風力観測题解及翻译(四舍五入)
YOLO V7源码解析
Windows系统使用Nginx部署Vue
网络面试-0x08如何理解CDN?
【Java基础】List集合概述、特点、特有方法、案例及List集合子类的特点
- 原文地址:https://blog.csdn.net/qq_40943760/article/details/125238788