一种基于混合策略的灰狼优化算法

摘要：灰狼优化算法作为一种群体智能算法，不可避免地会产生陷入局部寻优和收敛速度慢的问题。本文提出一种混合的改进策略，把动态权重和动态种群的结合起来，在提高收敛速度的同时，产生较好的解。

1.灰狼优化算法

基础灰狼算法的具体原理参考，我的博客：https://blog.csdn.net/u011835903/article/details/107716390

2. 改进灰狼优化算法

提出一种动态权重策略，基于权重的个体狼位置计算如式（6）,（7）所示 。
$$w_1=\frac{\left|X_1\right|}{\left|X_1\right|+\left|X_2\right|+\left|X_3\right|},w_2=\frac{\left|X_2\right|}{\left|X_1\right|+\left|X_2\right|+\left|X_3\right|},w_3=\frac{\left|X_3\right|}{\left|X_1\right|+\left|X_2\right|+\left|X_3\right|}\text{\hspace{1em}(6)}$$

$$X(t+1)=\left(w_1{X}_1+w_2{X}_2+w_3{X}_3\right)/3\text{\hspace{1em}(7)}$$

动态权重策略是一种对迭代过程进行改进的策略 ，能够很大程度上提高灰狼优化算法的收敛速度，但全局搜索能力并不是很好。

采用动态种群的思想，每一次迭代完成后，把适应度值较低的一半个体狼信息进行改变，可以及时地跳出局部寻优。基于动态种群的计算如式（8）~（11）所示 ，这 4 个公式并不是按顺序依次执行，而是每个公式以 1/4 的概率执行。
$$X(t+1)=X_{\alpha }\pm (ub-lb\cdot r+lb)\text{\hspace{1em}(8)}$$

$$X(t+1)=X_{\beta }\pm (ub-lb\cdot r+lb)\text{\hspace{1em}(9)}$$

$$X(t+1)=X_{\delta }\pm (ub-lb\cdot r+lb)\text{\hspace{1em}(10)}$$

$$X(t+1)=X_{\delta }\pm (ub-lb\cdot r+lb)\text{\hspace{1em}(11)}$$

本文对迭代过程进行改进，通过把动态权重和动态种群结合起来，提出一种混合策略的灰狼优化算法。
改进后的灰狼优化算法主要步骤：
（1）在狼群变量的上限和下限中随机初始化狼群和初始化算法参数。
（2）计算每个个体狼的适应度值。
（3）选择适应度排在前 3 的个体狼作为 , $\alpha ,\beta ,\delta$ 狼。
（4）根据式（1）,（2）,（3）,（6）,（7）计算其它狼的位置。
（5）重新计算所有个体狼的适应度值。

3.实验结果

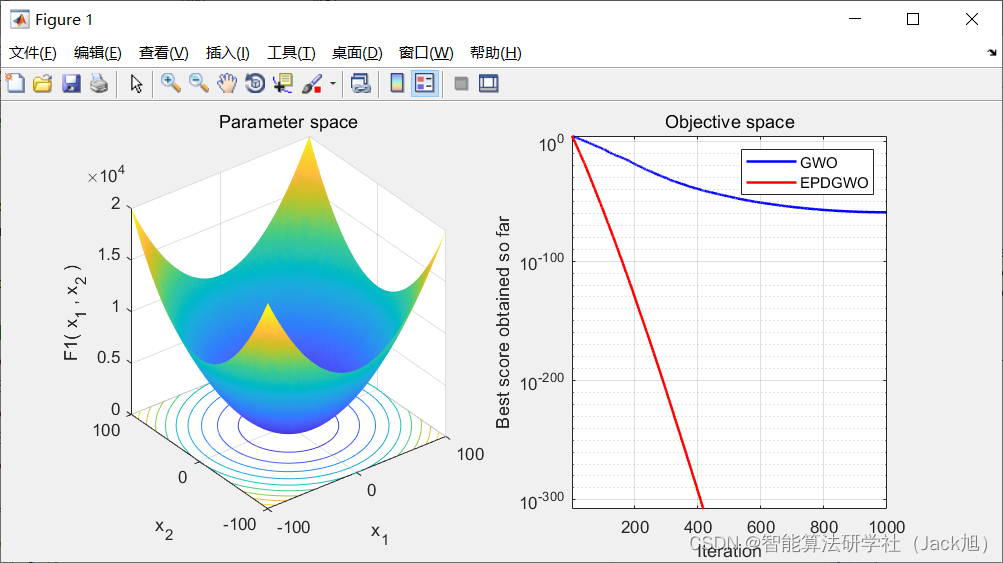
4.参考文献

[1]牛家彬,王辉.一种基于混合策略的灰狼优化算法[J].齐齐哈尔大学学报(自然科学版),2018,34(01):16-19+32.

5.Matlab代码

6.Python代码