本章是系列文章的第六章,介绍了循环的分析方法。循环优化的逻辑相对简单,但对性能提升的效果却非常明显。循环优化的分析还产生了一个图灵奖。
本文中的所有内容来自学习DCC888的学习笔记或者自己理解的整理,如需转载请注明出处。周荣华@燧原科技
6.1 循环的重要性
- 90/10定律,90%的算力消耗在10%的代码上,这些代码绝大多数都是各种循环
- 循环的优化对获得更高的性能非常重要
- 基于循环的迭代空间转换的优化(本章不涉及)
- 维持循环的迭代空间不变进行的优化(本章重点):
- 代码提升(code hoisting)
- 强度削减(strength reduction)
- 循环展开(loop unrolling)
- 等等
6.2 分解控制流图
对于下面的C代码,分析一下有几重循环?怎么从控制流图中定义循环?
1 #include <stdio.h> 2 int main(int argc, char **argv) { 3 int sum = 0; 4 int i = 1; 5 while (i < argc) { 6 char *c = argv[i++]; 7 while (*c != '\0') { 8 c++; 9 sum++; 10 } 11 } 12 printf("sum = %d\n", sum); 13 }
控制流图的生成方法就不多说了,忘记的同学可以回过头去看看第二章(2.1.3 LLVM),生成的svg图如下:
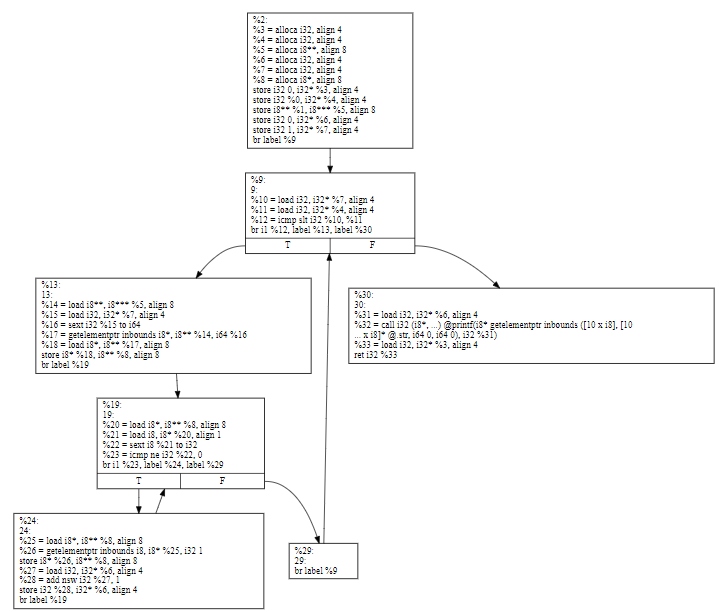
控制流图中的自然循环是具有下列属性的节点的集合S:
- 存在一个头结点h
- S中的任意一个元素都存在路径到头结点h
- S外不存在任何节点有边指向S中除h意外的其他节点
编译器中说的循环(loop)和拓扑意义上的环(cycle)是不同的。编译器领域中的环只能有一个入口,多个入口的环在编译器领域不叫做循环,因为绝大多数对循环的优化在多入口的环中都不适用。
多个入口的环在编码过程中也非常罕见,所以也不是编译器需要关心的场景。
6.2.1 控制流图的简化过程
如果对于边(n1, n2),n1是n2的唯一前驱,或者n1和n2是强连通图的一部分,可以用下面的方法简化:
- 删除边(n1, n2)
- 新建节点n12
- 将所有n1的前驱改成n12的前驱
- 将所有n2的后继改成n12的后继
- 删除节点n1和n2
重复上述操作,直到控制流图保持不变。
例如下面的控制流图:
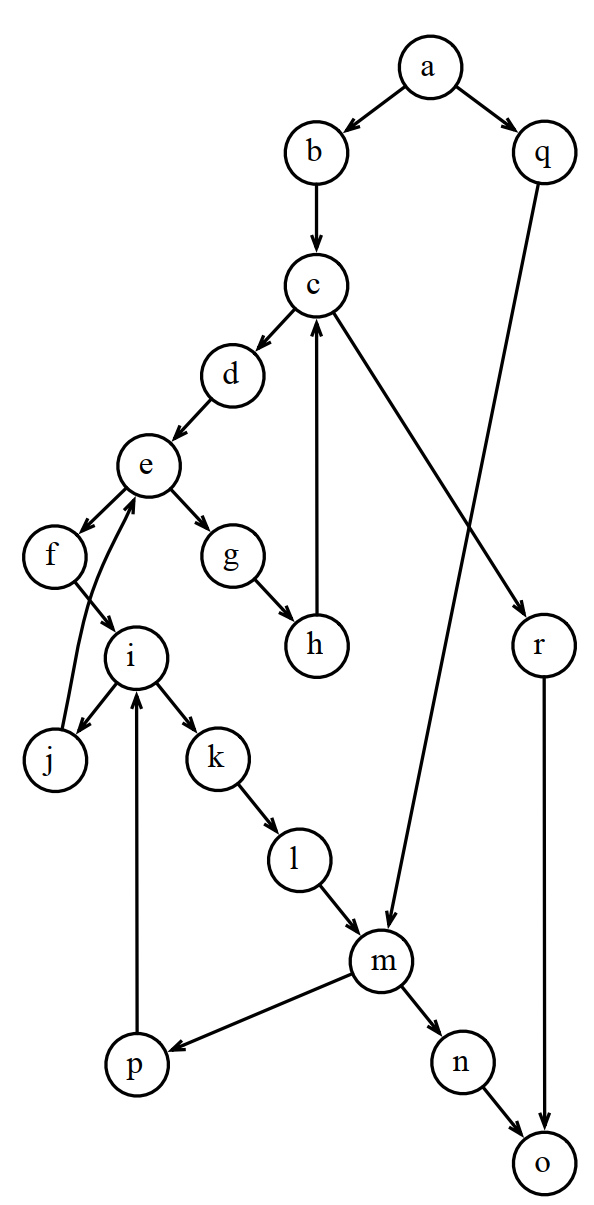
简化流程是这样的:


为什么要简化控制流图:
- 入口单一,可以在优化过程中在头结点处增加 冗余代码
- 简化后的图数据流分析速度更快
- 常规的循环语法,例如for,while,repeat,continue和break都会产生可简化的控制流图
- goto会产生不可简化的流图
6.3 自然循环
6.3.1 支配节点(Dominators)
节点d是节点n的支配节点,当且仅当所有从控制流图入口到n的所有路径都经过d。
D[s0] = {s0} D[n] = {n} ∪ (∩ p∈ pred[n]D[p]), for n ≠ s0
支配节点的计算:

6.3.2 直接支配节点(Immediate Dominators)
每个阶段n都 只有唯一一个直接支配节点idom(n),定义如下:
- idom(n) 不是n
- idom(n)是n的支配节点
- idom(n)不是n的其他支配节点的支配节点
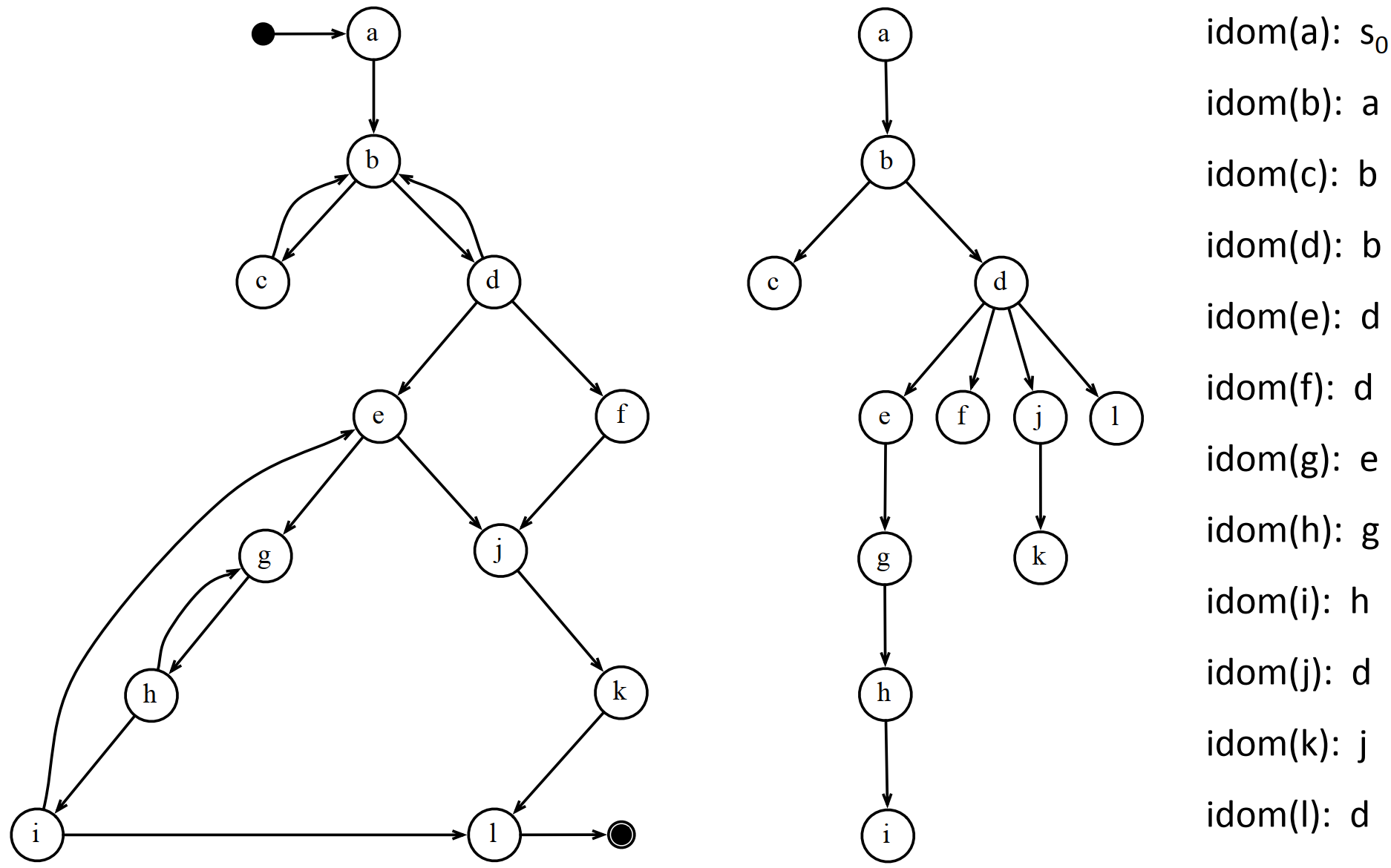
6.3.3 支配节点树(Dominator Tree)
把每个节点的直接支配节点画一条边到该节点,就形成了图的支配节点树:
循环的头节点h:在循环的节点集中,存在一个节点n,h是它的支配节点,并且存在边(n, h)。
如果两个循环的头结点存在支配关系,则被支配的头节点所在的循环称为内循环,支配的头节点所在的循环称为外循环。
6.4 安全的不变代码提升(SAFE INVARIANT CODE HOISTING)
6.4.1 循环不变性
如果某个计算在循环的每次迭代中都产生同样的值,则该计算时循环不变的。
循环不变表达式的通常优化方法是将该表达式提升到循环外。
满足下面任意一条要求的表达式是循环不变表达式:
- 表达式的参数是常量
- 表达式的参数定义在循环外
- 表达式的参数是循环不变表达式,并且在该表达式之前没有其他定义
将循环不变表达式提升到循环外的做法称为代码提升。
6.4.2 安全的不变代码提升
在程序点d,如果满足下面3个条件,可以对表达式t = a + b 安全的进行代码提升:
- d是所有t生效区域内节点的支配节点
- t在循环内只有一个定义
- t在循环的头结点外没有使用
6.4.3 循环倒置(Loop Inversion)
将常规的while循环转换成repeat-util循环的做法称为循环倒置。倒置后的循环可以安全的进行不变代码提升。
repeat-utill循环在循环过程中每次迭代只需要进行一次跳转,所以性能也比常规的while循环要好。
6.5 因变量(INDUCTION VARIABLES)
6.5.1 基本概念
基本因变量(Basic induction variable):如果一个变量i在循环内部仅定义一次,并且每次定义都是在原有值基础上增加或者减少循环不变量的值。
派生因变量(Derived induction variables):如果一个变量k在循环内部仅定义一次,并且k是一个因变量与循环不变量的乘积或者和。
i系列的派生因变量(a derived induction variable in the family of i):如果一个变量k定义中使用的因变量j仅定义一次,并且定义在循环内部,在j和k之间没有i的定义。
6.5.2 强度削减
将乘法运算换算成加法运算。例如下面的优化:

强度削减的算法基本上就是将派生因变量转换成基本因变量。算法过程一般如下:
- 对所有j = i * c, 假定变量i每个迭代增加b,i 初始化为a,那j每个迭代就要增加 b*c。
- 在循环外新增一个变量j'为第一次迭代时的j的值, j' = a*c
- 在循环外新增一个变量k,用来保存每个迭代j需要增加的值b*c
- 这样循环内部就可以优化成
- j = j'
- j' += k
6.5.3 无用代码删除(Dead Code Elimination)
首先删除的是j',因为k'已经完成了类似的功能:
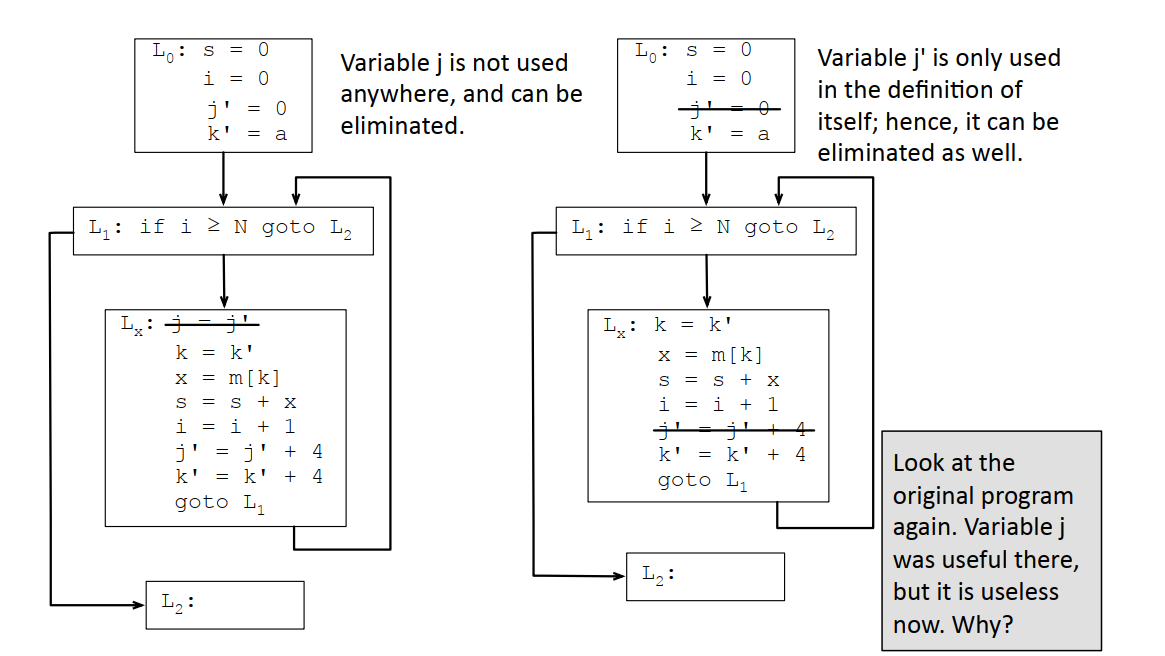
由于i除了定义就只有和循环不变量的比较,所以实际上i也是可以删除的:
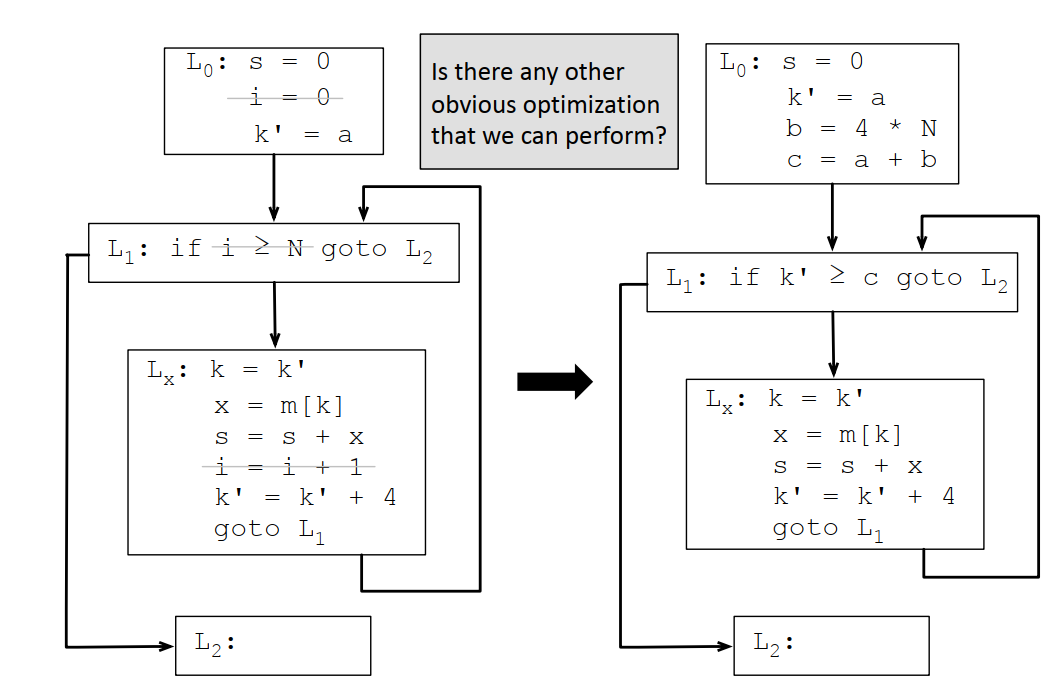
删除冗余拷贝:

循环倒置:
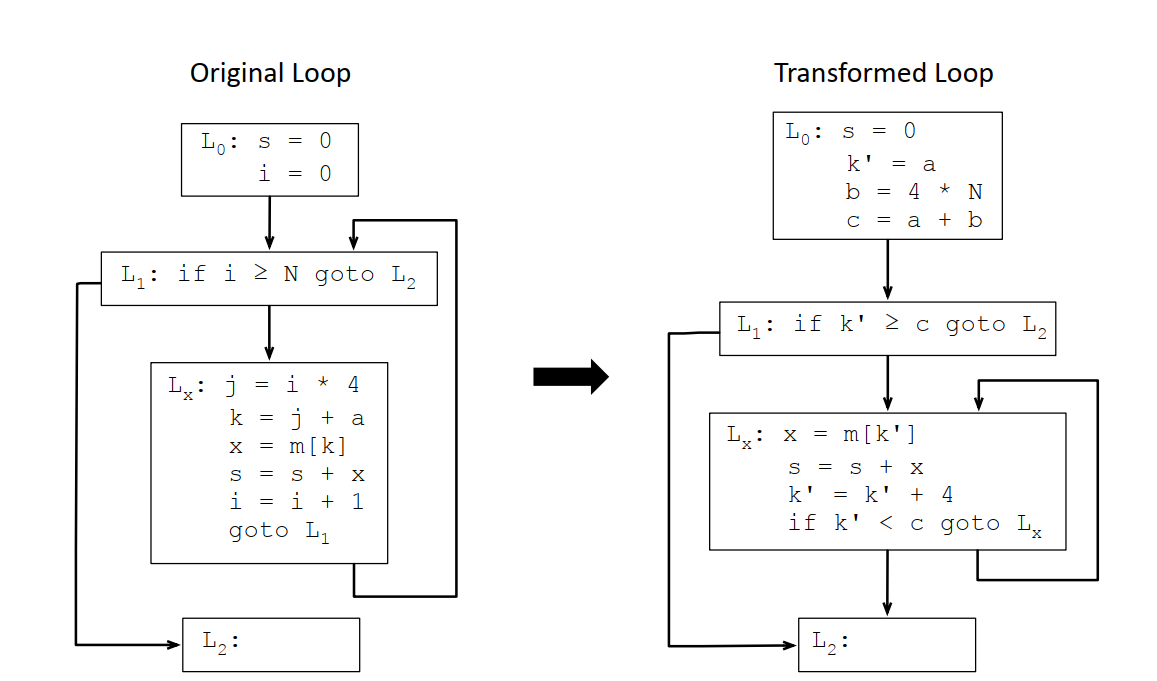
初始版本和最终优化版本的对比:
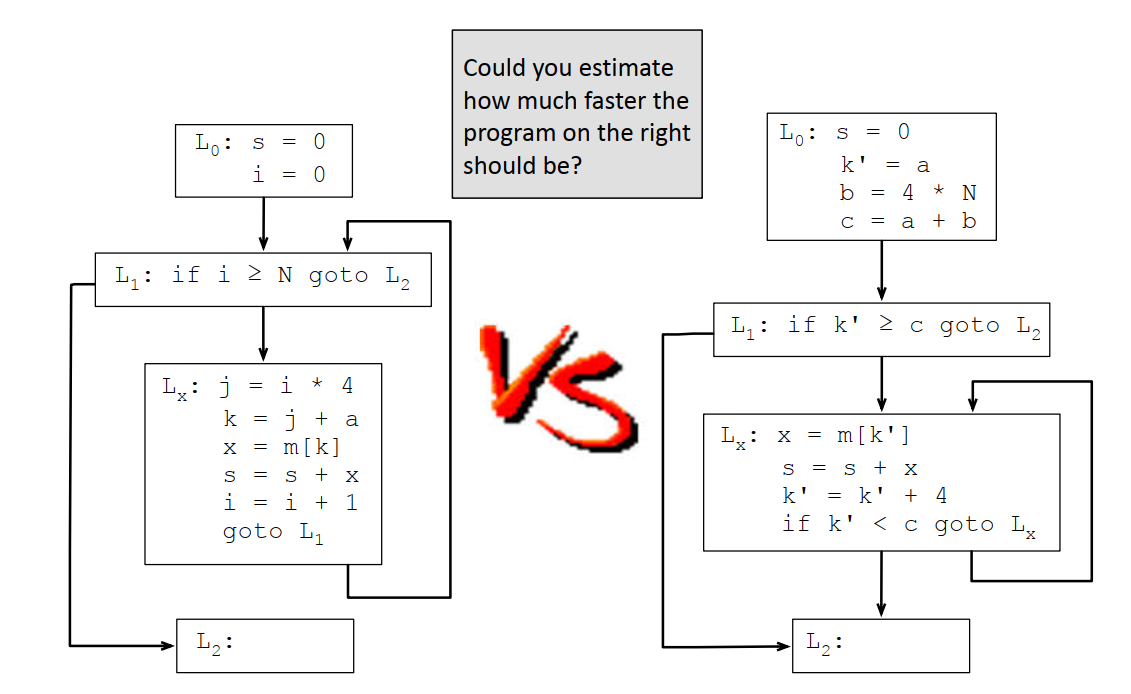
6.5.4 循环展开
循环展开是通过减少循环次数并增加循环内部的计算来优化的一种方式。例如对下面的代码:

以2为因子进行循环展开之后的结果是这样的:

6.5.5 指针分析简史
- Lowry, E. S. and Medlock, C. W. "Object Code Optimization". CACM 12(1), 13-22 (1969) 引入因变量优化和支配节点的概念
- Allen, F. E. "Control Flow Analysis". SIGPLAN Notices 23(7) 308-317 (1970)引入控制流图的化简,并因此获得图灵奖