一、理论基础

1、均衡优化算法

请参考这里。

2、多策略融合改进的均衡优化算法

（1）高破坏性多项式突变策略

引入高破坏性多项式突变策略初始化种群，其主要优点是即使决策变量的当前值接近搜索空间下边界或上边界，也能够探索决策变量的整个搜索范围。因此，引入高破坏性多项式突变初始化种群不仅可以丰富种群的多样性，而且可以提高种群中更优初始解所占的比例，为算法全局寻优奠定较好的基础，其伪代码如下图所示：

图1 高破坏性多项式突变策略伪代码

图中，$r$为$[0,1]$间随机数，$P_m$是突变概率，分布指数${\eta }_m$是一个非负数。

（2）差分变异的重构均衡池策略

受灰狼优化算法的启发，通过差分变异的方法添加三个精英候选粒子替换$X_{eq,ave}$，达到重构均衡池的目的，提高算法选择其他粒子的机率，促进粒子间信息交流，其数学模型如式(1)~(4)所示：$$X_{eq,ave1}=(X_{eq1}+X_{eq2})/2\text{\hspace{1em}(1)}$$$$X_{eq,ave2}=(X_{eq1}+X_{eq2}+X_{eq3})/3\text{\hspace{1em}(2)}$$$$X_{eq,ave3}=(X_{eq1}+X_{eq2}+X_{eq3}+X_{eq5})/4\text{\hspace{1em}(3)}$$$$X_{eq5}=\{\begin{array}{l}{X}_{eq1}+\mu \times (X_{eq2}-X_{eq3})T\le \frac{T_{\max }}{2}\\ \mu \times \left(|X_{eq1}-X_{eq2}|+|X_{eq3}-X_{eq4}|\right)T>\frac{T_{\max }}{2}\end{array}\text{\hspace{1em}(4)}$$其中，$X_{eq,ave1}$、$X_{eq,ave2}$、$X_{eq,ave3}$分别为三个精英候选粒子；$X_{eq5}$通过历史最优的四个粒子差分变异组成，帮助算法在迭代前期在全局范围内快速寻到更多优质粒子，在迭代后期逐渐接近最优粒子，保持种群多样性，降低算法陷入局部最优的概率。在差分变异过程中，$\mu$作为尺度因子一般为固定值，不利于算法在解空间进行全方位的搜索，因此本文将固定值$\mu$调整为随迭代次数自适应变化的双曲正切因子，其数学模型如式(5)所示：$$\mu =(T/T_{\max })\cdot \tanh \left(1-\frac{T}{T_{\max }}\right)\cdot \psi \text{\hspace{1em}(5)}$$其中，调节因子$\psi =3$，控制曲线平滑度。
MEO算法重构的均衡池数学模型如式(6)所示： X e q , p o o l = { X e q 1 , X e q 2 , X e q 3 , X e q , a v e 1 , X e q , a v e 2 , X e q , a v e 3 } (6) X_{eq,pool}=\{X_{eq1},X_{eq2},X_{eq3},X_{eq,ave1},X_{eq,ave2},X_{eq,ave3}\}\tag{6} Xeq,pool​={Xeq1​,Xeq2​,Xeq3​,Xeq,ave1​,Xeq,ave2​,Xeq,ave3​}(6)与$X_{eq,ave}$相比，更新$X_{eq,ave1}$、$X_{eq,ave2}$有利于算法在最优解周围进行深度开发，引领个体逐步趋近最优值，提高算法的收敛精度和速度，更新$X_{eq,ave3}$使算法具有更丰富的种群多样性，提高算法的收敛精度和速度，增强算法跳出局部最优的能力。

（3）$S$型变换因子

固定系数$m_1$不随算法迭代自适应变化，可能导致算法兼顾全局勘探和局部开采能力不足，从而不能完整体现实际的寻优过程。为解决这个问题，本文提出一种$S$型变换因子来改进$m_1$，其数学模型如式(7)所示：$$m_1=2\times \text{log}sig\left(\frac{0.5\times T_{\max }-T}{\varphi }\right)\text{\hspace{1em}(7)}$$其中，$\varphi$是调节$S$型变换因子$\text{log}sig()$斜率的系数。

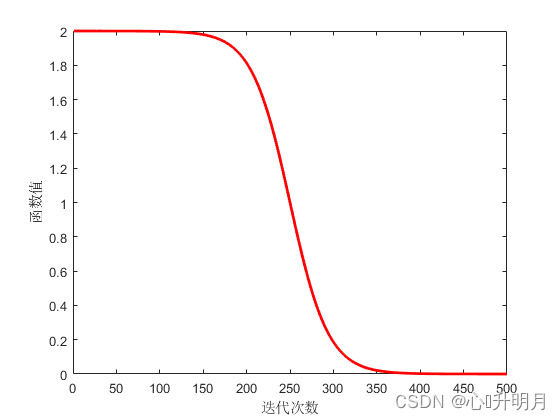
图2 $S$型变换因子的变化趋势图

由图2可知，在迭代前中期全局搜索时，$S$值较大，算法在更大范围动态探索，寻找潜在的优质粒子。$S$值随迭代次数增加非线性递减，算法的开发性能逐步增强并尽可能在最优粒子周围精细搜索，以平衡算法全局搜索和局部开发能力。
同时，借鉴柯西分布函数在原点处的峰值较小且在两端的分布较长的思想，使算法能以更短时间探索更多未知区域的优质粒子，使得粒子搜索变得更加多样化。因此，最终指数项函数$F$的数学模型如式(8)所示：$$F=m_1\times sign(r-cauchy(0,1))\times (e^{-\lambda \times t}-1)\text{\hspace{1em}(8)}$$

（4）动态螺旋搜索策略

受鲸鱼优化算法(Whale Optimization Algorithm, WOA)螺旋式搜索猎物方式的启发，引入一种动态螺旋搜索策略优化粒子浓度位置更新过程，使得候选粒子引导种群进行大范围的快速探索，开发更多的位置更新路径，其数学模型如式(9)所示：$$X=X_{eq}+\xi \cdot e^l\cdot \cos (2\pi l)\cdot (X-X_{eq})\cdot F+\frac{G}{\lambda \cdot V}\cdot (1-F)\text{\hspace{1em}(9)}$$其中，$l$是$[-1,1]$间的随机数；系数$\xi$决定螺旋形状。
鲸鱼在每次螺旋搜索时以固定螺旋路径接近猎物，导致搜索方式单一，易使算法陷入局部最优，从而削弱了算法的搜索能力。为此，提出随迭代次数自适应变化的参数$\xi$，动态调整螺旋形状，拓宽粒子搜索未知区域的能力，提高算法的寻优性能，动态螺旋参数$\xi$的数学模型如式(10)所示：$$\xi =0.5\cdot e^{\log ((0.05/2)\cdot (T/T_{\max }))}\text{\hspace{1em}(10)}$$由上式可知，动态螺旋参数$\xi$随迭代次数的增加自适应减小。具体来说，在算法迭代前中期$\xi$保持一个相对较大值，引导算法找到更多优质粒子，在迭代后期$\xi$保持一个相对较小值引导算法逼近全局最优粒子，通过动态螺旋变换增强算法搜索的深度和广度，降低粒子的趋同性，显着提高算法的寻优能力。

（5）MEO算法实现步骤

综上改进策略，文献[1]所提MEO算法执行步骤如下：
Step1：设置算法相关参数：种群规模$N$、最大迭代次数$T_{\max }$、问题空间维度$dim$、种群的可搜索空间$[X_{\min },X_{\max }]$；
Step2：采用高破坏性多项式突变初始化种群 { X i , i = 1 , 2 , ⋯   , N } \{X_i,i=1,2,\cdots,N\} {Xi​,i=1,2,⋯,N}，并计算种群中每个粒子的适应度值并选出四个适应度值最优的粒子$(X_{eq1},X_{eq2},X_{eq3},X_{eq4})$；
Step3：根据式(1)~(5)生成三个精英候选粒子$X_{eq,ave1},X_{eq,ave2},X_{eq,ave3}$，根据式(6)重构均衡池；
Step4：根据EO对应公式更新$t$，根据式(7)分别更新$m_1$，进而根据式(8)更新$F$；
Step5：根据EO对应公式更新$G$；
Step6：根据式(9)~(10)更新粒子浓度；
Step7：判断算法是否满足迭代终止条件，若满足，则迭代结束，输出最优位置$X_{eq1}$；否则，返回Step2，当前迭代次数$T=T+1$。

二、实验仿真与结果分析

将MEO与EO、BOA、GWO和ChOA进行对比，以文献[1]中表1的8个函数为例，实验设置种群规模为30，最大迭代次数为500，每种算法独立运算30次，结果显示如下：

函数：F1
EO：最差值: 1.0022e-39, 最优值: 5.3846e-44, 平均值: 8.4984e-41, 标准差: 2.1225e-40, 秩和检验: 3.0199e-11
BOA：最差值: 1.4444e-11, 最优值: 1.1123e-11, 平均值: 1.2701e-11, 标准差: 7.9368e-13, 秩和检验: 3.0199e-11
GWO：最差值: 3.6914e-26, 最优值: 3.2582e-29, 平均值: 2.3725e-27, 标准差: 6.6807e-27, 秩和检验: 3.0199e-11
ChOA：最差值: 3.8544e-06, 最优值: 4.4007e-09, 平均值: 7.7219e-07, 标准差: 1.1534e-06, 秩和检验: 3.0199e-11
MEO：最差值: 4.6237e-118, 最优值: 1.2409e-126, 平均值: 1.7019e-119, 标准差: 8.4223e-119, 秩和检验: 1
函数：F2
EO：最差值: 6.4439e-08, 最优值: 1.9733e-12, 平均值: 3.389e-09, 标准差: 1.1872e-08, 秩和检验: 3.0199e-11
BOA：最差值: 1.4741e-11, 最优值: 1.053e-11, 平均值: 1.2511e-11, 标准差: 1.2479e-12, 秩和检验: 3.0199e-11
GWO：最差值: 6.3855e-05, 最优值: 3.7551e-08, 平均值: 8.984e-06, 标准差: 1.5783e-05, 秩和检验: 3.0199e-11
ChOA：最差值: 1498.2054, 最优值: 0.19141, 平均值: 211.3187, 标准差: 389.7264, 秩和检验: 3.0199e-11
MEO：最差值: 1.7446e-87, 最优值: 7.5231e-110, 平均值: 5.8222e-89, 标准差: 3.185e-88, 秩和检验: 1
函数：F3
EO：最差值: 1.9372e-39, 最优值: 5.1406e-42, 平均值: 3.8546e-40, 标准差: 5.5732e-40, 秩和检验: 3.0199e-11
BOA：最差值: 1.4815e-11, 最优值: 1.1509e-11, 平均值: 1.3417e-11, 标准差: 8.0789e-13, 秩和检验: 3.0199e-11
GWO：最差值: 1.6403e-25, 最优值: 8.1809e-28, 平均值: 2.2271e-26, 标准差: 4.3215e-26, 秩和检验: 3.0199e-11
ChOA：最差值: 2.5151e-05, 最优值: 2.9527e-08, 平均值: 3.363e-06, 标准差: 4.9976e-06, 秩和检验: 3.0199e-11
MEO：最差值: 1.1145e-117, 最优值: 7.3901e-128, 平均值: 6.026e-119, 标准差: 2.0906e-118, 秩和检验: 1
函数：F4
EO：最差值: 8.1263e-08, 最优值: 4.3499e-17, 平均值: 6.0169e-09, 标准差: 1.5772e-08, 秩和检验: 3.0199e-11
BOA：最差值: 9.0526e-12, 最优值: 5.009e-14, 平均值: 4.9912e-12, 标准差: 3.0209e-12, 秩和检验: 3.0199e-11
GWO：最差值: 1.2747e-05, 最优值: 6.488e-09, 平均值: 1.9928e-06, 标准差: 2.4839e-06, 秩和检验: 3.0199e-11
ChOA：最差值: 4.0656, 最优值: 0.00014273, 平均值: 0.34252, 标准差: 0.77263, 秩和检验: 3.0199e-11
MEO：最差值: 2.1485e-21, 最优值: 3.4126e-41, 平均值: 7.9198e-23, 标准差: 3.9302e-22, 秩和检验: 1
函数：F5
EO：最差值: 0.99496, 最优值: 0, 平均值: 0.066331, 标准差: 0.25243, 秩和检验: 0.1608
BOA：最差值: 214.6623, 最优值: 0, 平均值: 33.0534, 标准差: 75.3688, 秩和检验: 1.9445e-09
GWO：最差值: 53.6229, 最优值: 0, 平均值: 4.5029, 标准差: 9.8465, 秩和检验: 4.5306e-12
ChOA：最差值: 28.7107, 最优值: 5.9584e-09, 平均值: 2.0144, 标准差: 6.1259, 秩和检验: 1.2118e-12
MEO：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数：F6
EO：最差值: 1.5099e-14, 最优值: 7.9936e-15, 平均值: 8.5857e-15, 标准差: 1.8853e-15, 秩和检验: 6.1337e-14
BOA：最差值: 6.8776e-09, 最优值: 5.2071e-09, 平均值: 6.014e-09, 标准差: 3.8511e-10, 秩和检验: 1.2118e-12
GWO：最差值: 1.4655e-13, 最优值: 7.5495e-14, 平均值: 1.0475e-13, 标准差: 1.8606e-14, 秩和检验: 1.1575e-12
ChOA：最差值: 19.9639, 最优值: 19.9577, 平均值: 19.9619, 标准差: 0.001424, 秩和检验: 1.2118e-12
MEO：最差值: 8.8818e-16, 最优值: 8.8818e-16, 平均值: 8.8818e-16, 标准差: 0, 秩和检验: NaN
函数：F7
EO：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
BOA：最差值: 9.9188e-12, 最优值: 1.1985e-12, 平均值: 4.5557e-12, 标准差: 2.2996e-12, 秩和检验: 1.2118e-12
GWO：最差值: 0.031022, 最优值: 0, 平均值: 0.0050148, 标准差: 0.01009, 秩和检验: 0.0055843
ChOA：最差值: 0.14168, 最优值: 3.4738e-08, 平均值: 0.018097, 标准差: 0.040515, 秩和检验: 1.2118e-12
MEO：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数：F8
EO：最差值: 5.0797e-06, 最优值: 2.1948e-25, 平均值: 1.7549e-07, 标准差: 9.2687e-07, 秩和检验: 3.0199e-11
BOA：最差值: 5.2141e-08, 最优值: 1.3673e-10, 平均值: 2.8471e-09, 标准差: 9.4927e-09, 秩和检验: 3.0199e-11
GWO：最差值: 0.0024731, 最优值: 1.0421e-16, 平均值: 0.000713, 标准差: 0.00069155, 秩和检验: 3.0199e-11
ChOA：最差值: 0.0014576, 最优值: 3.1246e-07, 平均值: 0.000187, 标准差: 0.00040906, 秩和检验: 3.0199e-11
MEO：最差值: 9.9348e-63, 最优值: 2.3857e-66, 平均值: 7.5592e-64, 标准差: 2.0083e-63, 秩和检验: 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

实验结果表明：所提MEO算法在收敛精度、收敛速度和稳定性上均表现出显著的优势。

三、参考文献

[1] 罗仕杭, 何庆. 多策略融合改进的均衡优化算法及其应用[J/OL]. 计算机工程与科学: 1-13 [2022-05-24].