一、设计要求

• 熟悉并掌握MATLAB中有关声音（wave）录制、播放、存储和读取的函数；

• 在MATLAB环境中，使用声音相关函数录制2秒左右自己的声音，抽样率是8000Hz；

• 分别取8000个和16000个数据进行频谱分析，得到幅度和相位谱，比较二者异同并分析原因；

• 针对电话信道（最高3500Hz），设计一个FIR或IIR滤波器进行滤波，把抽样率转变为7000Hz，并进行频谱分析，得到幅度和相位谱；

• 把处理后的所有数据储存为声音文件，与原始声音进行比较。

二、 原理简介

1.MATLAB中声音获取

1. 录制：

recObj = audiorecorder(fs,8,2)，抽样率fs, 8位数据，2通道,recObj为audiorecorder类。

recordblocking(recObj,2),录2秒 钟

2. 播放

play(输入参数为audiorecorder类) 或 sound（输入参数为语音信号数据，向量或矩阵形式，还要输入抽样率）

3. 存储

y = getaudiodata(recObj), 获取时域语音信号数据y，向量或矩阵形式, 以后处理都用这个数据

audiowrite(‘原始录音.wav’,y,fs)

4. 读取

[y,fs] = audioread('原始录音.wav');
1

2. 降采样

M倍的降采样，时域下每隔M1个点抽取一个点形成新的信号；频域下频谱扩展了M倍，周期仍为2π，幅度变为原来的1/M.

3. 滤波

IIR滤波器

IIR的冲击响应h[n]为无限长。根据所要设计滤波器的参数去确定一个模拟滤波器的传输函数H(s)，然后再根据这个传输函数，通过双线性变换、或脉冲响应不变法来进行数字滤波器的设计。

选用巴特沃斯滤波器。巴特沃斯滤波器的特点是通带内的频率响应曲线最大限度平坦，没有起伏，而在阻带则逐渐下降为零。

巴特沃斯低通滤波器可用如下振幅的平方对频率的公式表示：

其中，n为滤波器的阶数，ωc为截止频率，即振幅下降为3分贝时的频率。

设计时需要指定通带边界频率wp（归一化的），阻带边界频率ws，通带的波纹系数Rp, 阻带最小衰减Rs. 调用MATLAB函数buttord可自动计算出巴特沃斯滤波器的参数：阶数N, 截止频率wc. 见如下命令。

[N,wc]=buttord(wp,ws,Rp,Rs)

[num,den]=butter(N,wc) 该命令可以生成传递函数的分子num与分母den的系数向量。

yf=filter(num,den,y) 将滤波器作用于语音时域数据y，得到滤波后的yf.

FIR滤波器

FIR的冲击响应h[n]为有限长。使用窗函数法设计时域的系统函数h[n]。理想的h[n]为无限长sinc函数，需要加窗来限定为有限长，于是频域下变为有过渡带，阻带有波动的滤波器。选的窗不同，阻带最小衰减不同。

MATLAB命令 num=fir1(N,wc) 指定阶数N, 截止频率wc, 可生成Hamming窗的传递函数系数num

IIR, FIR的选择

从性能上来说，IIR滤波器传递函数包括零点和极点两组可调因素，对极点的惟一限制是在单位圆内。因此可用较低的阶数获得高的选择性，所用的存储单元少，计算量小，效率高。但是这个高效率是以相位的非线性为代价的。选择性越好，则相位非线性越严重。FIR滤波器传递函数的极点固定在原点，是不能动的，它只能靠改变零点位置来改变它的性能。所以要达到高的选择性，必须用较高的阶数；对于同样的滤波器设计指标，FIR滤波器所要求的阶数可能比IIR滤波器高510倍，结果，成本较高，信号延时也较大；如果按线性相位要求来说，则IIR滤波器就必须加全通网络进行相位校正，同样要大大增加滤波器的阶数和复杂性。而FIR滤波器却可以得到严格的线性相位。

从使用要求上来看，在对相位要求不敏感的场合，如语言通信等，选用IIR较为合适，这样可以充分发挥其经济高效的特点；对于图像信号处理，数据传输等以波形携带信息的系统，则对线性相位要求较高，如果有条件，采用FIR滤波器较好。

三、实验步骤

1. 用MATLAB录音2秒(抽样率8000)，存储声音文件，获得时域音频数据y. 编写了record函数，输出音频数据y。

2. 将y做fft变换，画出幅度(abs)和相位(angle)谱。取y的8000个数据（2倍降采样）做fft变换，画出幅度和相位谱。编写了process_draw（y）函数，音频数据y作为输入参数。

3. 重新录制抽样率为7000的语音。设计IIR 巴特沃斯低通滤波器，对语音进行处理。

利用freqz函数画出滤波器的频谱图，画出语音信号处理前后的频谱图。为了更好展现滤波效果，幅值使用对数坐标，单位分贝，MATLAB公式：20*log10(abs(Y))

其中Y为fft的结果。

播放、存储处理后的语音。编写了yf=process_filter（y）函数，输入为处理前语音数据y，输出为处理后语音数据yf.

四、结果分析

1.录音结果

采用双通道录音，效果会比单通道好。上图为时域波形数据，双通道的数据几乎重合。录音时，开始的1秒无法录入语音。

2. 分别取8000个和16000个数据进行频谱分析

录音的抽样率为8000Hz,录音2秒，总共得到16000个数据点。取8000个数据点进行频谱分析，相当于对音频进行2倍的降采样。

绘制频谱图时，频率轴采用归一化的数字频率，截取fft变换的前半部分显示，对应数字角频率0π。因为频谱是关于π对称的。

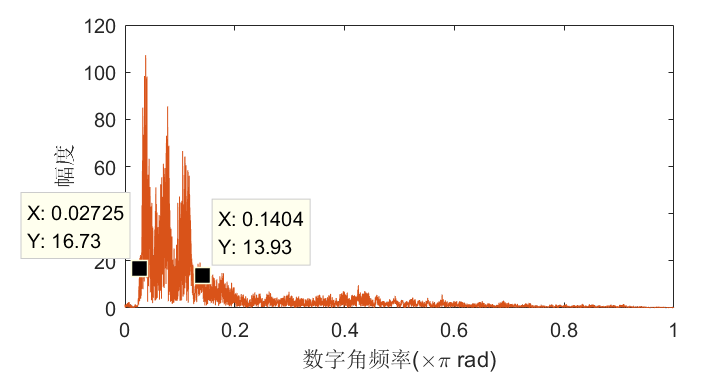
上图结果显示，语音信号的幅度集中在0.03π至0.14π之间，对应模拟频率为0.034000=120Hz到0.144000=560Hz之间。

上图为2倍降采样前后频谱的对比，可见幅度近似变为了原来的0.5倍，而频率近似扩展到原来的2倍，符合理论预期。结果并不是完全精确的理论的倍数，因为原信号在数字频率0.5以上仍有微小的幅度分量，2倍降采样后，该部分会造成混叠。

3. 抽样率转变为7000Hz进行录音，进行低通滤波

• IIR滤波器

上图为巴特沃斯滤波器的频谱图，滤波器参数为：通带边界频率ωp=0.16π，阻带边界频率ωs=0.3π，通带的波纹系数Rp=0.42, 阻带最小衰减Rs=100dB。语音滤波前后的幅度谱（分贝）和相位谱见下图。可见0.2π左右幅度大幅衰减。

播放滤波后的语音信号，发现声音更加低沉，因为滤掉了高频成分。

• FIR滤波器

上图为N=50, 截止频率0.16π的Hamming窗的幅度相位频谱图，可见在00.2π范围内为线性相位。

上图为滤波前后的幅度谱（分贝）和相位谱。可见0.2π以后衰减至20dB以下。

播放滤波后的语音信号，发现声音更加低沉，因为滤掉了高频成分。

五、 补充内容

为了更好地验证滤波器的效果，对原始音频加单频噪声，即时域数据加上一个cos信号，其频谱为单频的脉冲。下图为加了噪声后的时域波形，可见几乎完全将原始语音信号覆盖。

再使用IIR滤波，滤波器参数与上面相同

滤波前后频谱图见上图。可见0.3π左右加了一个单频噪声，播放录音时完全将语音盖住。滤波后，该噪声的幅度大幅度衰减，播放音频，不会再听到噪音。

六、附录

代码：

有四个函数文件：record, process_draw, process_filter, add_noise

运行示例，命令行依次输入：

Hz抽样率录音，画频谱图）

Hz抽样率录音，滤波）

（加噪声后滤波）

function y=record()
close all
fs=7000;
%取样频率
duration=2;
%录音时间2s
disp('按任意键开始录音')
pause
recObj = audiorecorder(fs,8,2);
%抽样率fs 8位数据 2通道
disp('开始录音')
recordblocking(recObj, duration);
% 录音录2秒钟
disp('结束录音');
% 回放录音数据
play(recObj);
% 获取录音数据
y = getaudiodata(recObj);
audiowrite('原始录音.wav',y,fs)
function process_draw(y)
%y为两通道，16000*2
close all
fs=8000;
%取样频率
duration=2;
%录音时间2s
t=linspace(0,duration,duration*fs);
% 绘制录音数据波形
figure
plot(t,y);
xlabel('时间/s')
ylabel('时域波形')
n=size(y,1);
%n 采样点个数
f=(0:n/2-1)/n*2;
%归一化的数字频率 前一半频谱
fd=f(2:2:end);
yd=y(2:2:end,:);
%抽取一半 降采样
Y=fft(y);
Yd=fft(yd);
Y=Y(1:n/2,:);
%画出前一半频谱，角频率0-pi
Yd=Yd(1:n/4,:);
figure
subplot(221)
plot(f,abs(Y))
xlabel('数字角频率(\times\pi rad)')
ylabel('幅度')
subplot(222)
plot(f,angle(Y))
xlabel('数字角频率(\times\pi rad)')
ylabel('相位')
subplot(223)
plot(fd,abs(Yd))
xlabel('数字角频率(\times\pi rad)')
ylabel('降采样后幅度')
subplot(224)
plot(fd,angle(Yd))
xlabel('数字角频率(\times\pi rad)')
ylabel('降采样后相位')
function yf=process_filter(y)
close all
%下面为IIR巴特沃斯滤波器设计
wp=0.16;
%通带边界频率
ws=0.3;
%阻带
Rp=0.42;
%通带波纹系数
Rs=100;
%最小阻带衰减
[N,wc]=buttord(wp,ws,Rp,Rs)
[num,den]=butter(N,wc);
%下面为FIR hanning滤波器设计
% N=50;
% wc=0.16;
% num=fir1(N,wc);
% Hamming window 
% den=1;
%FIR滤波器传递函数分母为1
figure(1)
freqz(num,den)
yf=filter(num,den,y);
%滤波后
sound(yf,7000)
audiowrite('IIR滤波后.wav',yf,7000)
n=size(y,1);
%n 采样点个数
f=(0:n/2-1)/n*2;
%归一化的数字频率 前一半频谱
Y=fft(y);
Yf=fft(yf);
Y=Y(1:n/2,:);
%画出前一半频谱，角频率0-pi
Yf=Yf(1:n/2,:);
figure(2)
% 绘制滤波前后频谱
subplot(221)
plot(f,20*log10(abs(Y)))
xlabel('数字角频率(\times\pi rad)')
ylabel('幅度(dB)')
subplot(222)
plot(f,angle(Y))
xlabel('数字角频率(\times\pi rad)')
ylabel('相位')
subplot(223)
plot(f,20*log10(abs(Yf)))
xlabel('数字角频率(\times\pi rad)')
ylabel('滤波后幅度(dB)')
subplot(224)
plot(f,angle(Yf))
xlabel('数字角频率(\times\pi rad)')
ylabel('滤波后相位')
function yn=add_noise(y)
fs=7000;
n=size(y,1);
%n 采样点个数
%noise=0.1*randn(n,1);
%加白噪声
fn=1000;
n=10*cos(fn*[1:n])';%加单频噪声
noise2=[n n];
yn=y+noise2;
sound(yn,fs)
audiowrite('加单频噪声后录音.wav',yn,fs)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126