**

基于STM32控制的旋转倒立摆

**

---

前言

近期在学习简易旋转倒立摆装置，倒立摆其实是一个十分经典的自动控制模型，不过开始学习了解结构和原理还是花了很多时间，在思路以及调试过程中遇到了很多困难。
我认为倒立摆有两个难点，一个是自动起摆一个是机械结构，其中自动起摆涉及到PID算法与运动方程的求解，而机械结构主要是尽量减小转动阻尼同时避免旋转时线的缠绕。我买了平衡小车家的机械结构套件，他们为了避免线缠绕使用了导线环，这是一个好东西，可以完美解决导线缠绕问题。主要想讲一下我做的整个过程以及反思总结。

---

一、旋转倒立摆的结构

整个机械结构主要是三个部分用于带动整个结构运动的电机，一个测量主动摆位置的编码器，以及一个测量摆杆位置的编码器。查阅资料后发现两者是有区别的，一个是相对编码器（测量主动摆位置），一个是绝对编码器（测量随动摆位置的），下面会主要介绍什么是增量式编码器与绝对编码器。

1.相对编码器与绝对编码器

增量式编码器：增量式旋转编码器在电机旋转时输出脉冲。 要使用增量编码器确定轴
位置， 必须知道起始位置并使用外部电路来计算输出脉冲数。
绝对编码器：绝对旋转编码器输出对应于旋转角度的数字代码。 无需计算脉冲就能了解电机轴的位置。 只需要读取编码器的数字输出。
增量式编码器的特点：增量式编码器非常适合测速度，可无限累加测量。但是存在零点累计误差，抗干扰较差，接收设备的停机需断电记忆，开机应找零或参考位等问题。增量式编码器只输出设备的位置变化和运动方向，不会输出设备的绝对位置。
绝对编码器的特点：角位移传感器为单圈绝对值编码器，由机械位置决定的每个位置是唯一的（每个位置的高低电平不同），不需要找参考点，抗干扰性较强,一般用来测量位置位移。
简单来说增量编码器就是通过是输出脉冲让后让单片机计数脉冲数来算速度，绝对编码器就是直接输出角度变化的数字量。而我使用的是增量式编码器中的增量式霍尔编码器。霍尔编码器是一种通过磁电转换将输出轴上的机械几何位移量转换成脉冲或数字量的传感器。霍尔编码器是由霍尔码盘和霍尔元件组成。霍尔码盘是在一 定直径的圆板上等分地布置有不同的磁极。霍尔码盘与电动机同轴，电动机旋转时，霍尔元件检测输出若干脉冲信号，为判断转向，一般输出两组存在一定相位差的方波信号。

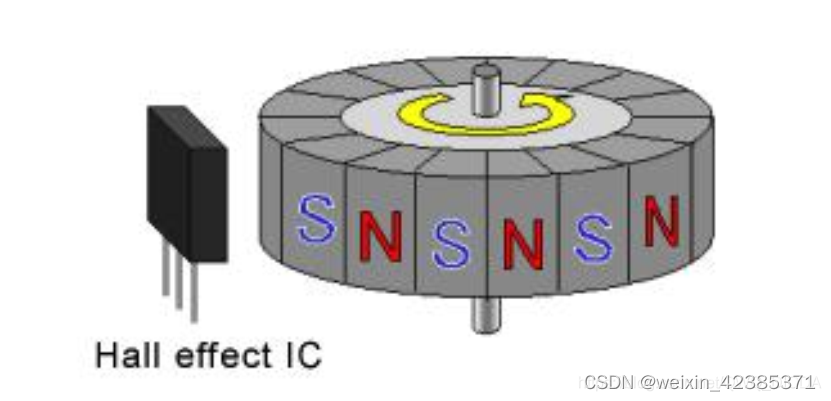
2.相对编码器与绝对编码器的信号采集

知道了两种编码器的工作方式就能清楚地知道如何去使用了，其中增量式霍尔编码器通过计算编码器产生的脉冲个数从而获取运动方向和速度。绝对编码器其实核心是一个电位器，它的阻值会随着旋转角度不同而不同。 这里使用的是STM32的编码器模式获取增量式霍尔编码器的信号。绝对编码器主要是使用单片机的AD采样功能获取它的信号。

3.STM32编码器模式

在STM32中，编码器使用的是定时器接口，通过数据手册可知，定时器1，2，3，4，5和8有编码器的功能，而其他没有。编码器输入信号TI1,TI2经过输入滤波，边沿检测产生TI1FP1，TI2FP2接到编码器模块，通过配置编码器的工作模式，即可以对编码器进行正向/反向计数。

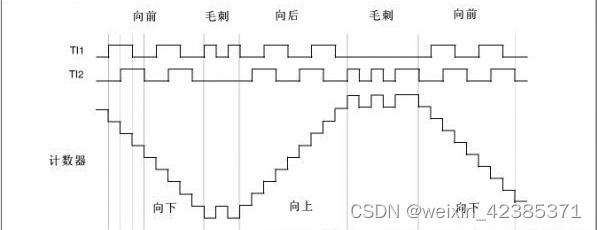
STM32编码器有三种工作模式，其中模式三即为上文中提到的四倍频模式。

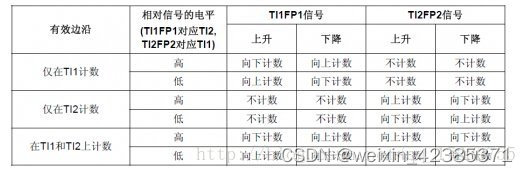
4.使用STM32CubeMx配置过程

（1） 首先打开timer3的encoder模式：

（2） 下面才是重点，配置具体定时器的参数：

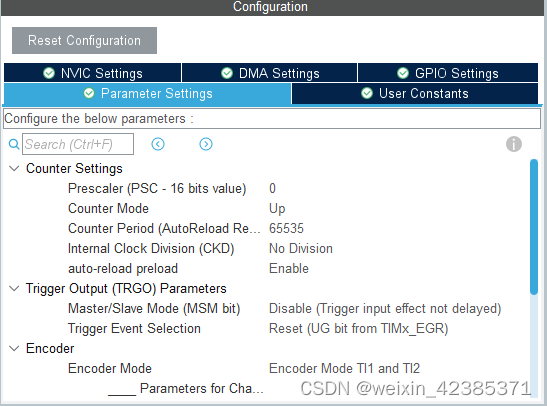
选择的encoderMode是 TI1和TI2模式。这种模式下，AB两相的上升沿和下降沿都会计数，所以计数值是实际值的4倍，需要做分频。还有个地方需要解释一下，我刚开始的时候就是把这里的设置没搞清楚，看Polarity参数设置的是Rising Edge。这个参数的意思是在检测到上升沿的时候就触发encoder捕获AB相的值，而并不是这里设置的是上升沿就只检测AB相的上升沿，下降沿还是同样会计数的。Input Filter滤波值是从1-15，看情况设定，是用来滤除一些杂波的。
（3） 生成代码这样基本就配置好了，生成mdk工程。然后就是添加应用代码了。在初始化中添加打开定时器的encoder模式：

HAL_TIM_Encoder_Start(&htim3, TIM_CHANNEL_ALL);
1

然后定期调用下面这一句函数就可以获取到encoder编码器的计数值：

enc1 = (uint32_t)(__HAL_TIM_GET_COUNTER(&htim3));//获取定时器的值
1

二、倒立摆模型建立

通过牛顿力学公式，在较为理想的情况下（无摩擦，主动摆、随动摆都是质量均匀的刚体）对倒立摆系统进行建模。



可以发现倒立摆系统在右半平面存在极点，它是一个不稳定的系统，同时它也是一个非线性系统。

三、实验方案与实验现象

1.整体方案

倒立摆是一种非线性、不稳定系统，而PID控制对于线性系统控制效果较好，对于倒立摆系统的建模是通过将目标值附近进行线性化得到的传递函数模型，进而通过PID控制将系统调控的稳定。对于初始位置离目标值较远，近似线性化模型已经不太吻合，PID就达不到很好的控制效果。所以起始阶段选用能量控制，让倒立摆运动到适合PID控制的位置。

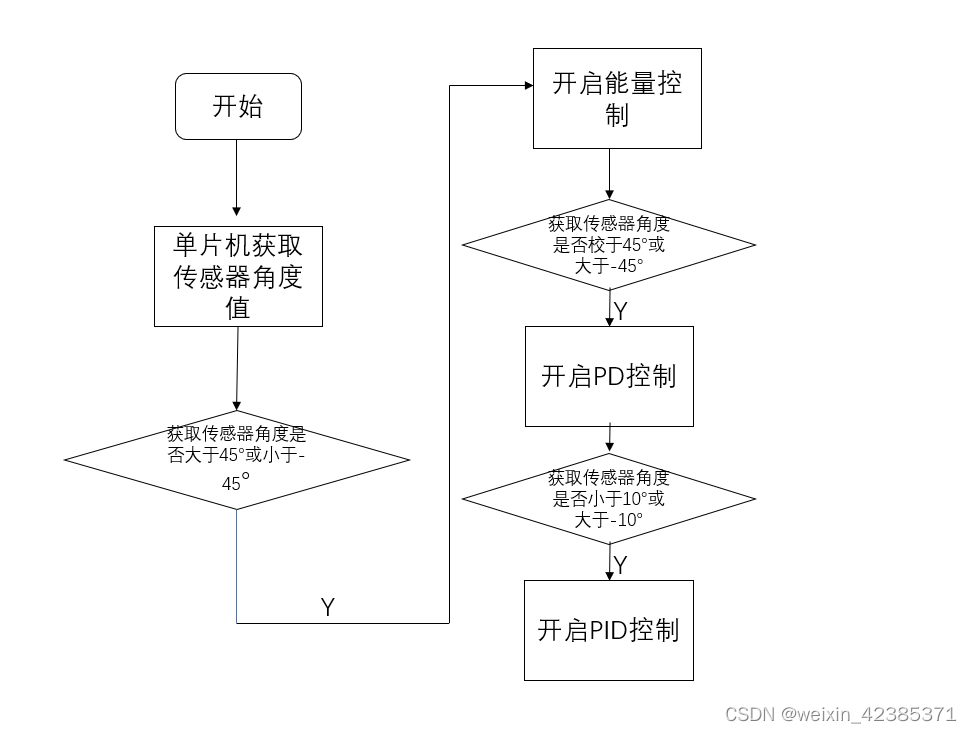
关于能量控制：

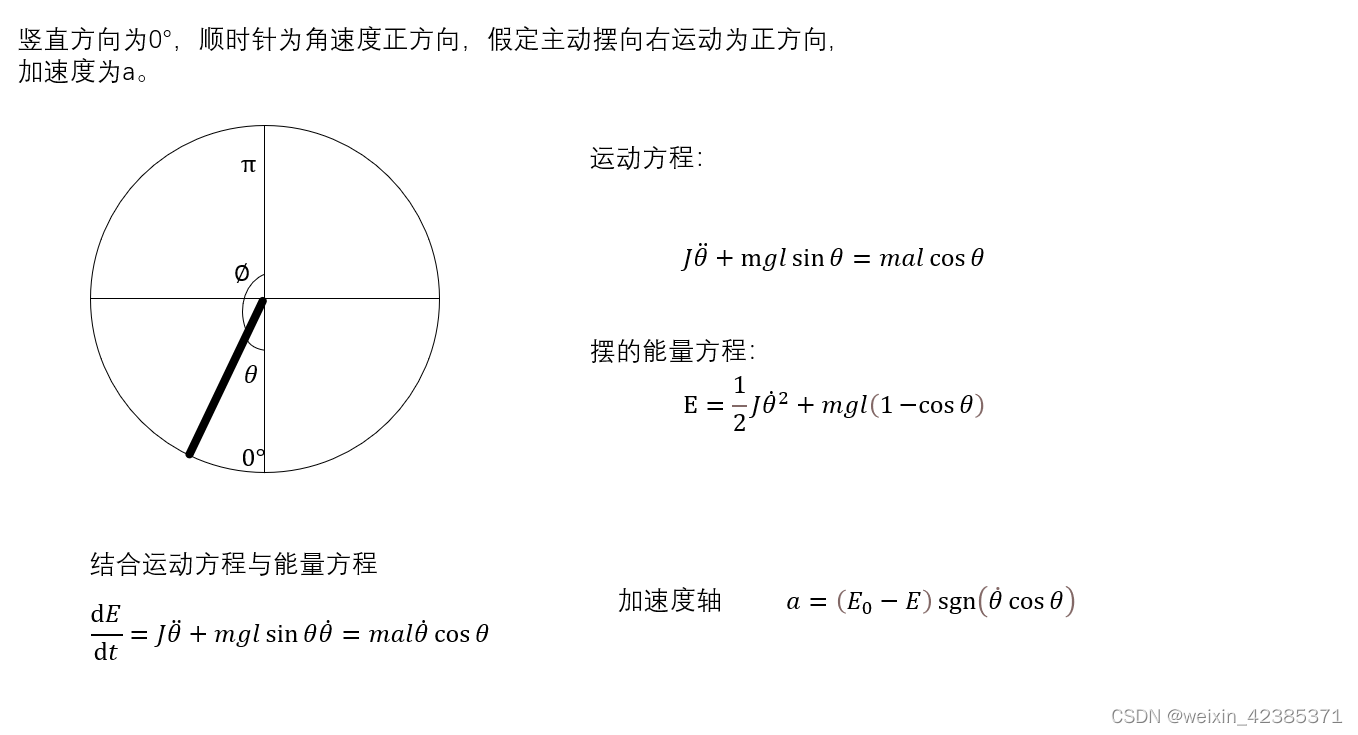
摆杆的能量其实是一个系数可以改变的积分，所以给定了能量控制策略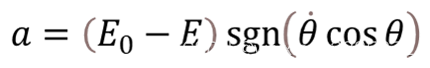
摆杆一共有a>0,𝜃>0;a>0,𝜃<0;a<0,𝜃>0;a<0,𝜃<0;(a为摆杆加速度）四种运动状态，开始给摆杆一个速度，随后摆杆会摆会到𝜃=0，但是速度不为0，此时给倒立摆一个与摆杆运动方向相反的速度，之后摆杆状态为a<0,𝜃<0；等再次𝜃=0时，速度不为0，此时再次给倒立摆一个与摆杆运动方向相反的速度，之后会重复a>0,𝜃<0;a<0,𝜃>0;这两个状态，倒立摆能量就会积攒，最后达到目标位置附近。
部分代码如下：

//能量控制
	float w0 = (float)sqrt((double)(mP*g*Lk)/Inertia);
	float E = ((mP*g*Lk)/2)*(((pow((double)(pendulum_speed/w0),2))) + cos(pendulum_angle) - 1);
	float torque_swing = Kv*(E-E0)*sign(pendulum_speed*cos(pendulum_angle));
	return torque_swing;
1
2
3
4
5

//角度控制
int balance(float Angle)
{  
   float Bias;                       //倾角偏差
	 static float Last_Bias,D_Bias;    //PID相关变量
	 int balance;                      //PWM返回值 
	 Bias=Angle-ZHONGZHI;              //求出平衡的角度中值 和机械相关
	 D_Bias=Bias-Last_Bias;            //求出偏差的微分 进行微分控制
	 balance=PID.Balance_KP*Bias + D_Bias*PID.Balance_KD;   //===计算倾角控制的电机PWM  PD控制
   Last_Bias=Bias;                   //保持上一次的偏差
	 return balance;
}
1
2
3
4
5
6
7
8
9
10
11
12

2.实验现象与上位机数据

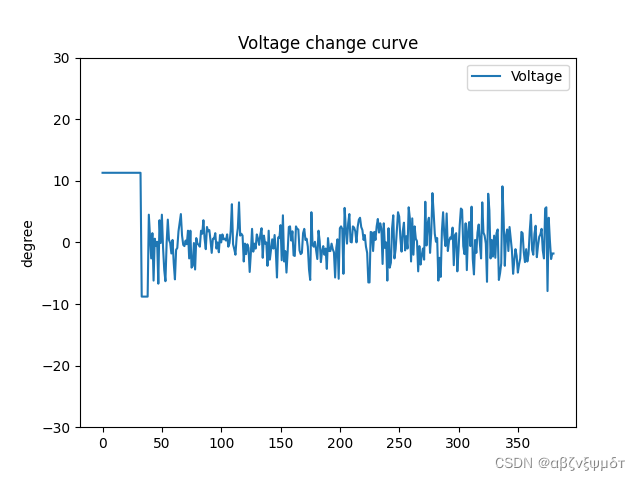
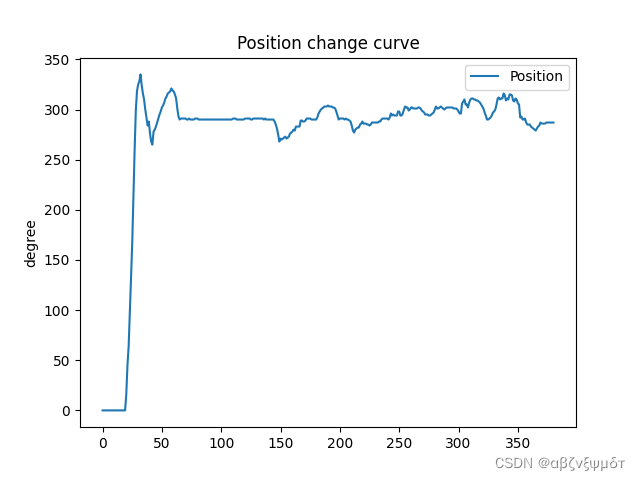
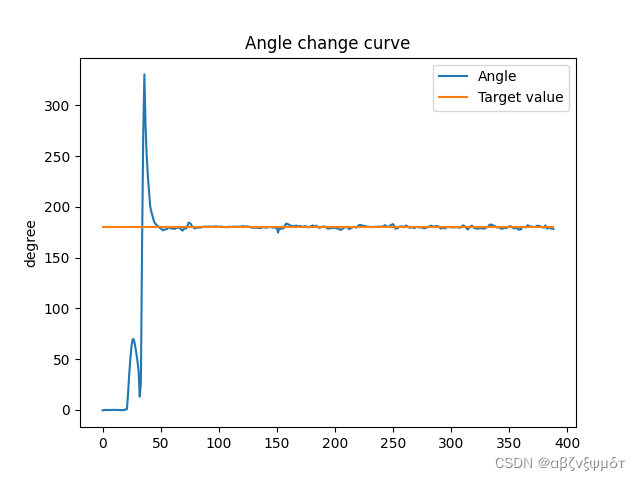
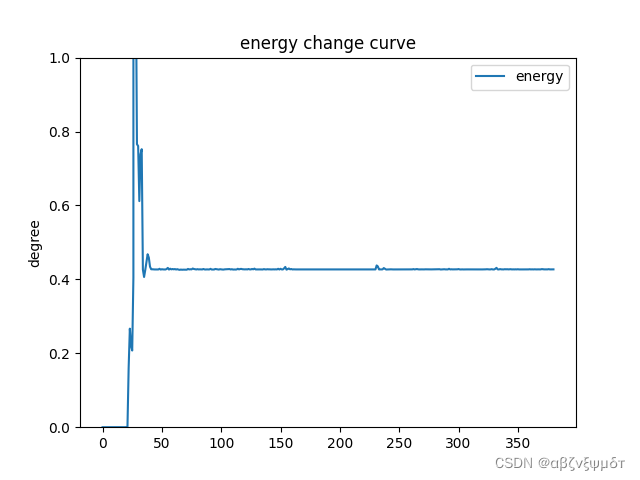
通过串口发送数据我获取了倒立摆电机电压，位置传感器的值，以及角度传感器的值，从图中可以看出倒立摆角度基本能维持在180°附近，但位置有少许波动，但基本能在很小范围内稳定，效果能基本符合预期。
起摆过程是比较理想的开始给予一次速度后，在到达角度为0的时候给予摆臂和摆杆相反方向的速度，两次能量给予过后倒立摆就能到达目标位置附近。位置也能基本稳定在一个小范围内，第二幅图中后半部分是人为加入扰动之后位置的值，可以看出倒立摆能基本为定在目标位置附近，但是不如最初稳定，其次单片机AD采样的数值由于有噪声会有跳动，虽然已经将AD采样的值转化为角度，但是会有±1°左右的误差，这会导致目标位置时刻在变化，所以倒立摆会时刻调整弥补这种误差，这是电压有时候跳变较大的原因。从采集的数据来看实验现象基本与理论相符合，但抗干扰性较差，说明实验PID值还需要进一步调整，但基本现象符合预期。
最后的能量曲线也可看出能量基本维持不变，中间有一段能量跳变是因为经过传感器的死区传感器数值存在较大的跳变这会导致速度产生突变进而获得的能量数值不准确，所以我选择基于能量是判断角度为0根据速度方向，从而去给电机与摆杆相反运动方向的电压就可避免因为死区存在电压跳变而导致能量突变的问题。

反思与总结

1. 完成以上这个小任务是花费了很长时间的，前前后后两个月，主要的问题体现在三个方面包括基础知识的欠缺、思路不是很明确、心态的调整方面。整个倒立摆任务的完成需要理解机械结构、确定方案以及涉及相应的代码。首先是机械结构，倒立摆的机械结构其实就是一个电机两个编码器，但刚开始AB式增量式霍尔编码器不太明白怎么使用，花了一定时间才查到资料怎么用STM32编码器获取数据的。最主要的问题是使用摆杆上的角度编码器的时候，没有去测试每一根线是做什么用的，举个例子AB式增量霍尔编码器一共是六根线，两根是电机供电、两根是编码器供电、两根是编码器的脉冲，角度编码器只有三根线，因为它的原理就是一个电位器，这是犯得一个比较低级的错误，误认为中间的一根线为改变阻值的线（因为一般电位器都是两边为定值），这导致后面控制摆杆运动的时候由于数据获取不准确一直没有正常的效果，最大的问题出现在开始了解结构上，应该是一步一步测试知道怎么用。
2. 方案的选定上其实找了很多别人的方案，不过是只拿到了程序，有很多小的地方不够理解，只是看着别人的现象成功，不够理解别人是如何实现的。总结来说就是思路不够清楚，单纯的看别人代码去了，代码可能只是每个人都是对的，但是不一定适用每个人的机械结构，具体的应该是理解原理自己进行微调，也就是说需要一个完整的正确的方案，再去开始实施，不然只看代码，对于调控硬件来说，不会起到什么作用，相反会因为一些机械结构反应和别人不一样而特别困惑。整个环节实现以后，其实去查了一些资料包括系统的建模，方案为什么使用等一些原理，其实更有助于帮助理解整个倒立摆系统，单一的看代码其实本末倒置，后续调起来也比较浪费时间。
3. 其次比较大的问题就是，相关单片机的知识有一段时间没有用过了，很多都忘了，整个倒立摆系统要用到定时、中断、AD采样、PWM波输出、串口通信等功能，是一步一步看着视频一个功能一个功能学习的，中间出现了很多各种各样的问题，主要原因都是不太熟悉单片机这一块，每一个功能调试也浪费了一些时间。
4. 最后是做的整个过程中在心态方面的问题，因为时间很长，在中间一段时间其实是比较困惑的，方向不对，查资料很多不适合或者导师给的资料需要很久才能看懂等等，有一段时间比较没进度、没方向，所以心态也比较差，这就导致做事效率比较低，是一个恶性循环，之后的学习中是需要尽快调整这种不好的状态的。
   整个小任务做完以后，其实收获还是很多的，最重要的是学会遇到问题的解决方式，先查资料怎么去做，再去一步步get小细节，先有大方向再去做小的一步一步的，对于这次的任务来说直接的体现形式其实就是一段代码，但只看代码其实起不了很大的作用，相反出现不同的现象也不知道怎么解决会浪费更多的时间。其次对于PID的理解以及单片机的一些基本功能的使用也有了更一步的了解，以前不熟悉或者忘记的部分有了更深的理解。