• 数据结构和算法 数论 中国余数定理

    1、中国余数定理概述

            找出所有整数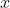x，它们被3、5、7除时，余数分别为2，3和2。一个这样的解为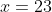x = 23，所有的解是形如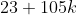23 + 105k(k为任意整数)的整数。“中国余数定理”提出，对一组两两互质的模数（如3、5、7）来说，其取模运算的方程组与对其积（如105）取模运算的方程之间存在着一种对应关系。

            中国余数定理被广泛用于计算大整数，因为它允许用几个类似的小整数计算来替换一个知道结果大小界限的计算。

            定理定义如下：给定成对互质正整数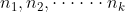n_1, n_2, \cdot \cdot \cdot \cdot \cdot \cdot n_k，和任意整数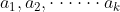a_1, a_2, \cdot \cdot \cdot \cdot \cdot \cdot a_k，同时同余系统

            

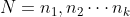            有解，且解是唯一的模N = n_1, n_2 \cdots n_k。

    2、应用示例

    1. 输入：num[] = {5, 7}, rem[] = {1, 3}
    2. 输出：31
    3. 解释：
    4. 31 是最小的数，使得：
    5.   (1) 当我们将它除以 5 时，我们得到余数 1。
    6.   (2) 当我们将它除以 7 时，我们得到余数 3。
    7.  
    8. 输入：num[] = {3, 4, 5}, rem[] = {2, 3, 1}
    9. 输出：11
    10. 解释：
    11. 11 是最小的数，使得：
    12.   (1) 当我们将它除以 3 时，我们得到余数 2。
    13.   (2) 当我们将它除以 4 时，我们得到余数 3。
    14.   (3) 当我们将它除以 5 时，我们得到余数 1。

    3、应用场景描述

    （1）场景1

            2P/Encke彗星、4P/Faye彗星和8P/Tuttle彗星的轨道周期分别为 3 年、8 年和 13 年。这些彗星的最后一次近日点分别发生在 2017 年、2014 年和 2008 年。

            这三颗彗星都将在同一年达到近日点的明年是什么时候？

            对于这个问题，假设时间以整数年为单位，并且每个轨道周期都是常数。

    （2）场景2

            一所学校的学生人数在 500 到 600 人之间。如果我们将他们分成 12 人、20 人或 36 人一组，则总是剩下 7 名学生。这所学校有多少学生？

    4、代码实现

    （1）c++

    1. #include<bits/stdc++.h>
    2. using namespace std;
    3.  
    4. // k is size of num[] and rem[]. Returns the smallest
    5. // number x such that:
    6. // x % num[0] = rem[0],
    7. // x % num[1] = rem[1],
    8. // ..................
    9. // x % num[k-2] = rem[k-1]
    10. // Assumption: Numbers in num[] are pairwise coprime
    11. // (gcd for every pair is 1)
    12. int findMinX(int num[], int rem[], int k)
    13. {
    14. 	int x = 1; // Initialize result
    15.  
    16. 	// As per the Chinese remainder theorem,
    17. 	// this loop will always break.
    18. 	while (true)
    19. 	{
    20. 		// Check if remainder of x % num[j] is
    21. 		// rem[j] or not (for all j from 0 to k-1)
    22. 		int j;
    23. 		for (j=0; j<k; j++ )
    24. 			if (x%num[j] != rem[j])
    25. 			break;
    26.  
    27. 		// If all remainders matched, we found x
    28. 		if (j == k)
    29. 			return x;
    30.  
    31. 		// Else try next number
    32. 		x++;
    33. 	}
    34.  
    35. 	return x;
    36. }
    37.  
    38. int main(void)
    39. {
    40. 	int num[] = {3, 4, 5};
    41. 	int rem[] = {2, 3, 1};
    42. 	int k = sizeof(num)/sizeof(num[0]);
    43. 	cout << "x is " << findMinX(num, rem, k);
    44. 	return 0;
    45. }

    （2）Java

    1. import java.io.*;
    2.  
    3. class ZGYSDL {
    4. 	
    5. 	// k is size of num[] and rem[]. Returns the smallest
    6. 	// number x such that:
    7. 	// x % num[0] = rem[0],
    8. 	// x % num[1] = rem[1],
    9. 	// ..................
    10. 	// x % num[k-2] = rem[k-1]
    11. 	// Assumption: Numbers in num[] are pairwise coprime
    12. 	// (gcd for every pair is 1)
    13. 	static int findMinX(int num[], int rem[], int k)
    14. 	{
    15. 		int x = 1; // Initialize result
    16. 	
    17. 		// As per the Chinese remainder theorem,
    18. 		// this loop will always break.
    19. 		while (true)
    20. 		{
    21. 			// Check if remainder of x % num[j] is
    22. 			// rem[j] or not (for all j from 0 to k-1)
    23. 			int j;
    24. 			for (j=0; j<k; j++ )
    25. 				if (x%num[j] != rem[j])
    26. 				break;
    27. 	
    28. 			// If all remainders matched, we found x
    29. 			if (j == k)
    30. 				return x;
    31. 	
    32. 			// Else try next number
    33. 			x++;
    34. 		}
    35. 	
    36. 	}
    37. 	
    38. 	public static void main(String args[])
    39. 	{
    40. 		int num[] = {3, 4, 5};
    41. 		int rem[] = {2, 3, 1};
    42. 		int k = num.length;
    43. 		System.out.println("x is " + findMinX(num, rem, k));
    44. 	}
    45. }

    （3）Python

    1.  
    2. # k is size of num[] and rem[].
    3. # Returns the smallest number x
    4. # such that:
    5. # x % num[0] = rem[0],
    6. # x % num[1] = rem[1],
    7. # ..................
    8. # x % num[k-2] = rem[k-1]
    9. # Assumption: Numbers in num[]
    10. # are pairwise coprime (gcd for
    11. # every pair is 1)
    12. def findMinX(num, rem, k):
    13. 	x = 1; # Initialize result
    14.  
    15. 	# As per the Chinise remainder
    16. 	# theorem, this loop will
    17. 	# always break.
    18. 	while(True):
    19. 		
    20. 		# Check if remainder of
    21. 		# x % num[j] is rem[j]
    22. 		# or not (for all j from
    23. 		# 0 to k-1)
    24. 		j = 0;
    25. 		while(j < k):
    26. 			if (x % num[j] != rem[j]):
    27. 				break;
    28. 			j += 1;
    29.  
    30. 		# If all remainders
    31. 		# matched, we found x
    32. 		if (j == k):
    33. 			return x;
    34.  
    35. 		# Else try next number
    36. 		x += 1;
    37.  
    38. # Driver Code
    39. num = [3, 4, 5];
    40. rem = [2, 3, 1];
    41. k = len(num);
    42. print("x is", findMinX(num, rem, k));

    （4）c#

    1. using System;
    2.  
    3. class ZGYSDL
    4. {
    5. 	
    6. 	// k is size of num[] and rem[].
    7. 	// Returns the smallest
    8. 	// number x such that:
    9. 	// x % num[0] = rem[0],
    10. 	// x % num[1] = rem[1],
    11. 	// ..................
    12. 	// x % num[k-2] = rem[k-1]
    13. 	// Assumption: Numbers in num[]
    14. 	// are pairwise coprime
    15. 	// (gcd for every pair is 1)
    16. 	static int findMinX(int []num, int []rem,
    17. 						int k)
    18. 	{
    19. 		
    20. 		// Initialize result
    21. 		int x = 1;
    22. 	
    23. 		// As per the Chinese remainder theorem,
    24. 		// this loop will always break.
    25. 		while (true)
    26. 		{
    27. 			// Check if remainder of x % num[j] is
    28. 			// rem[j] or not (for all j from 0 to k-1)
    29. 			int j;
    30. 			for (j = 0; j < k; j++ )
    31. 				if (x % num[j] != rem[j])
    32. 				break;
    33. 	
    34. 			// If all remainders matched, we found x
    35. 			if (j == k)
    36. 				return x;
    37. 	
    38. 			// Else try next number
    39. 			x++;
    40. 		}
    41. 	
    42. 	}
    43. 	
    44. 	public static void Main()
    45. 	{
    46. 		int []num = {3, 4, 5};
    47. 		int []rem = {2, 3, 1};
    48. 		int k = num.Length;
    49. 		Console.WriteLine("x is " + findMinX(num,
    50. 										rem, k));
    51. 	}
    52. }

    （5）php

    1. <?php
    2.  
    3. // k is size of num[] and rem[].
    4. // Returns the smallest number x
    5. // such that:
    6. // x % num[0] = rem[0],
    7. // x % num[1] = rem[1],
    8. // ..................
    9. // x % num[k-2] = rem[k-1]
    10. // Assumption: Numbers in num[]
    11. // are pairwise coprime (gcd for
    12. // every pair is 1)
    13. function findMinX($num, $rem, $k)
    14. {
    15. 	$x = 1; // Initialize result
    16.  
    17. 	// As per the Chinise remainder
    18. 	// theorem, this loop will
    19. 	// always break.
    20. 	while (true)
    21. 	{
    22. 		// Check if remainder of
    23. 		// x % num[j] is rem[j]
    24. 		// or not (for all j from
    25. 		// 0 to k-1)
    26. 		$j;
    27. 		for ($j = 0; $j < $k; $j++ )
    28. 			if ($x % $num[$j] != $rem[$j])
    29. 			break;
    30.  
    31. 		// If all remainders
    32. 		// matched, we found x
    33. 		if ($j == $k)
    34. 			return $x;
    35.  
    36. 		// Else try next number
    37. 		$x++;
    38. 	}
    39.  
    40. 	return $x;
    41. }
    42.  
    43. // Driver Code
    44. $num = array(3, 4, 5);
    45. $rem = array(2, 3, 1);
    46. $k = sizeof($num);
    47. echo "x is " ,
    48. 	findMinX($num, $rem, $k);
    49.  
    50. ?>

    （6）javascript

    1. <script>
    2. 	
    3. // k is size of num and rem. Returns the smallest
    4. // number x such that:
    5. // x % num[0] = rem[0],
    6. // x % num[1] = rem[1],
    7. // ..................
    8. // x % num[k-2] = rem[k-1]
    9. // Assumption: Numbers in num are pairwise coprime
    10. // (gcd for every pair is 1)
    11. function findMinX(num , rem , k)
    12. {
    13. 	var x = 1; // Initialize result
    14.  
    15. 	// As per the Chinese remainder theorem,
    16. 	// this loop will always break.
    17. 	while (true)
    18. 	{
    19. 		// Check if remainder of x % num[j] is
    20. 		// rem[j] or not (for all j from 0 to k-1)
    21. 		var j;
    22. 		for (j=0; j<k; j++ )
    23. 			if (x%num[j] != rem[j])
    24. 			break;
    25.  
    26. 		// If all remainders matched, we found x
    27. 		if (j == k)
    28. 			return x;
    29.  
    30. 		// Else try next number
    31. 		x++;
    32. 	}
    33.  
    34. }
    35.  
    36. // Driver method
    37. var num = [3, 4, 5];
    38. var rem = [2, 3, 1];
    39. var k = num.length;
    40. document.write("x is " + findMinX(num, rem, k));
    41. </script>

  • 相关阅读:
    c++game大全
    科技+智慧+颜值，智慧公厕黑科技提升城市形象
    openGauss学习笔记-84 openGauss 数据库管理-内存优化表MOT管理-内存表特性-MOT部署服务器优化：x86
    用于包管理的基本命令APT-GET和APT-CACHE
    进军东南亚市场，腾讯云数据库 TDSQL 助力印尼 BNC 银行数字化转型
    Kalman滤波器的原理与实现
    【JVM】字节码技术：手撕 多态执行原理
    Vue3开始
    分布式ID（7）：Zookeeper实现分布式ID生成
    Linux debian gdb dump
  • 原文地址：https://blog.csdn.net/bashendixie5/article/details/124974861