在 二分搜索算法框架解析中，详细介绍了二分搜索的细节问题，探讨了「搜索一个元素」，「搜索左侧边界」，「搜索右侧边界」这三个情况，教你如何写出正确无 bug 的二分搜索算法。

但是前文总结的二分搜索代码框架仅仅局限于「在有序数组中搜索指定元素」这个基本场景，具体的算法问题没有这么直接，可能你都很难看出这个问题能够用到二分搜索。

所以本文就来总结一套二分搜索算法运用的框架套路，帮你在遇到二分搜索算法相关的实际问题时，能够有条理地思考分析，步步为营，写出答案。

原始的二分搜索代码

二分搜索的原型就是在「有序数组」中搜索一个元素 target，返回该元素对应的索引。

如果该元素不存在，那可以返回一个什么特殊值，这种细节问题只要微调算法实现就可实现。

还有一个重要的问题，如果「有序数组」中存在多个 target 元素，那么这些元素肯定挨在一起，这里就涉及到算法应该返回最左侧的那个 target 元素的索引还是最右侧的那个 target 元素的索引，也就是所谓的「搜索左侧边界」和「搜索右侧边界」，这个也可以通过微调算法的代码来实现。

**在具体的算法问题中，常用到的是「搜索左侧边界」和「搜索右侧边界」**这两种场景，很少有让你单独「搜索一个元素」。

「搜索左侧边界」的二分搜索算法的具体代码实现如下：

// 搜索左侧边界
int left_bound(int[] nums, int target) {
    if (nums.length == 0) return -1;
    int left = 0, right = nums.length;
    
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            // 当找到 target 时，收缩右侧边界
            right = mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid;
        }
    }
    return left;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

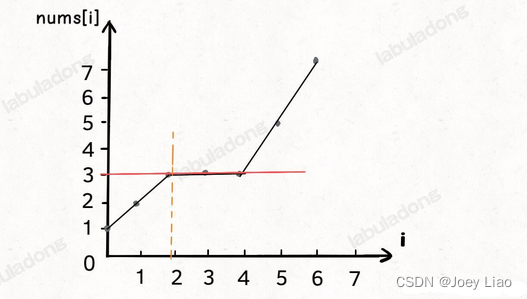
假设输入的数组 nums = [1,2,3,3,3,5,7]，想搜索的元素 target = 3，那么算法就会返回索引 2。

如果画一个图，就是这样：

「搜索右侧边界」的二分搜索算法的具体代码实现如下：
// 搜索右侧边界

int right_bound(int[] nums, int target) {
    if (nums.length == 0) return -1;
    int left = 0, right = nums.length;
    
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            // 当找到 target 时，收缩左侧边界
            left = mid + 1;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid;
        }
    }
    return left - 1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

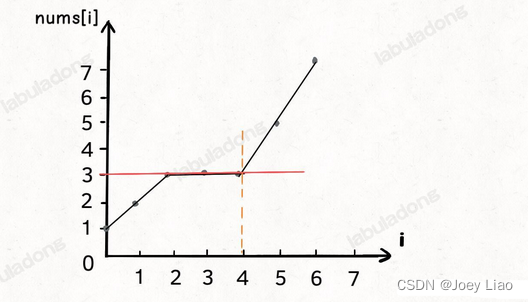
输入同上，那么算法就会返回索引 4，如果画一个图，就是这样：

二分搜索问题的泛化

什么问题可以运用二分搜索算法技巧？

首先，你要从题目中抽象出一个自变量 x，一个关于 x 的函数 f(x)，以及一个目标值 target。

同时，x, f(x), target 还要满足以下条件：

1. f(x) 必须是在 x 上的单调函数（单调增单调减都可以）
2. 题目是让你计算满足约束条件 f(x) == target 时的 x 的值。

运用二分搜索的套路框架

想要运用二分搜索解决具体的算法问题，可以从以下代码框架着手思考：

// 函数 f 是关于自变量 x 的单调函数
int f(int x) {
    // ...
}

// 主函数，在 f(x) == target 的约束下求 x 的最值
int solution(int[] nums, int target) {
    if (nums.length == 0) return -1;
    // 问自己：自变量 x 的最小值是多少？
    int left = ...;
    // 问自己：自变量 x 的最大值是多少？
    int right = ... + 1;
    
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (f(mid) == target) {
            // 问自己：题目是求左边界还是右边界？
            // ...
        } else if (f(mid) < target) {
            // 问自己：怎么让 f(x) 大一点？
            // ...
        } else if (f(mid) > target) {
            // 问自己：怎么让 f(x) 小一点？
            // ...
        }
    }
    return left;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

具体来说，想要用二分搜索算法解决问题，分为以下几步：

1. 确定 x, f(x), target 分别是什么，并写出函数 f 的代码。
2. 找到 x 的取值范围作为二分搜索的搜索区间，初始化 left 和 right 变量。
3. 根据题目的要求，确定应该使用搜索左侧还是搜索右侧的二分搜索算法，写出解法代码。

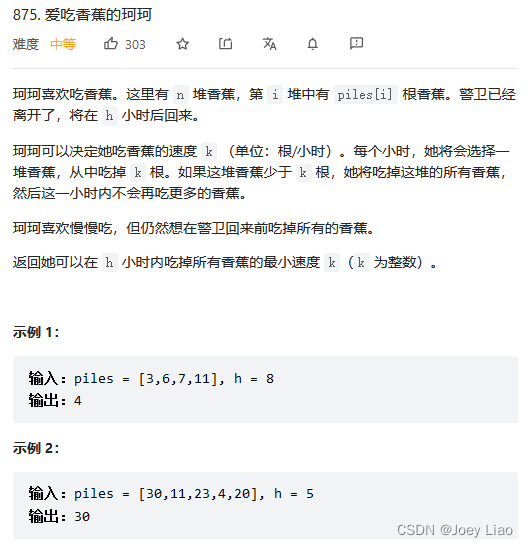
例题一：爱吃香蕉的珂珂

这是力扣第875题「爱吃香蕉的珂珂」:

1. 确定x,f(x), target分别是什么，并写出函数f的代码。

   自变量x是什么呢?回忆之前的函数图像，二分搜索的本质就是在搜索自变量。
   所以，题目让求什么，就把什么设为自变量，珂珂吃香蕉的速度就是自变量×。

   那么，在x上单调的函数关系f(x）是什么?
   显然，吃香蕉的速度越快，吃完所有香蕉堆所需的时间就越少，速度和时间就是一个单调函数关系。所以，f(x)函数就可以这样定义∶若吃香蕉的速度为x根/小时，则需要f(x)小时吃完所有香蕉。

//速度为k时，需要f(k)才能吃完所有香蕉
//f（k）随着k单调递减
public int f(int piles,int k){
    int res=0;
    for(int pile:piles){
        res+=(pile/k+pile%k==0?0:1); 
    }
    return res;
}
1
2
3
4
5
6
7
8
9

target自然就是吃香蕉的时间限制，是对f（x）返回值的最大约束

2. 找到x的取值范围作为二分搜索的搜索区间，初始化left和right变量。
   显然吃香蕉的最小速度为1，最大速度为piles数组中的最大值
3. 根据题目的要求，确定应该使用搜索左侧还是搜索右侧的二分搜索算法，写出解法代码。
   现在我们确定了自变量x是吃香蕉的速度，f(x）是单调递减的函数，target 就是吃香蕉的时间限制H，题目要我们计算最小速度，也就是x要尽可能小:
   
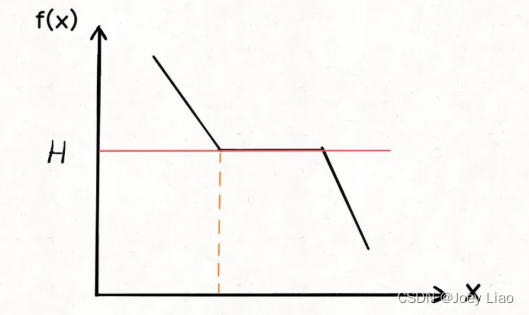
   这就是搜索左侧边界的二分搜索嘛，不过注意f(x）是单调递减的，不要闭眼睛套框架，需要结合上图进行思考，写出代码︰

class Solution {
    public int minEatingSpeed(int[] piles, int h) {
        int left=1,right=1000000000+1;
        while(left<right){
            int mid=left+(right-left)/2;
            if(f(piles,mid)==h){
                //搜索左侧边界，则需要收缩右侧边界
                right=mid;
            }else if(f(piles,mid)<h){
                //需要让f(x)的返回值大一点
                right=mid;
            }else{
                //需要让f(x)的返回值小一点
                left=mid+1;
            }
        }
        return left;
    }
    public int f(int[] piles,int k){
        int res=0;
        for(int pile:piles){
            res+=pile/k; 
            res+=pile%k==0?0:1;
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

例题二：运送货物

再看看力扣第1011 题「在D天内送达包裹的能力」:

1. 确定 x, f(x), target 分别是什么，并写出函数 f 的代码。
2. 找到 x 的取值范围作为二分搜索的搜索区间，初始化 left 和 right 变量。
3. 根据题目的要求，确定应该使用搜索左侧还是搜索右侧的二分搜索算法，写出解法代码。

class Solution {
    public int shipWithinDays(int[] weights, int days) {
        int left=0,right=1;
        for(int weight:weights){
            left=Math.max(left,weight);
            right+=weight;
        }
        while(left<right){
            int mid=left+(right-left)/2;
            if(f(weights,mid)<=days){
                //搜索左侧边界，则需要收缩右侧边界
                right=mid;
            }else{
                //需要让f(x)的返回值小一点
                left=mid+1;
            }
        }
        return left;
    }
    //x为运载能力
    //f（x）为运完的时间
    public int f(int[] weights,int x){
    		 int cnt=0,res=1;
        for(int weight:weights){
            if(cnt>=weight){
                cnt-=weight;
            }else{
                cnt=x-weight;
                res++;
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

例题三:分割数组的最大值

我们实操一下力扣第410题「分割数组的最大值」，难度为困难:

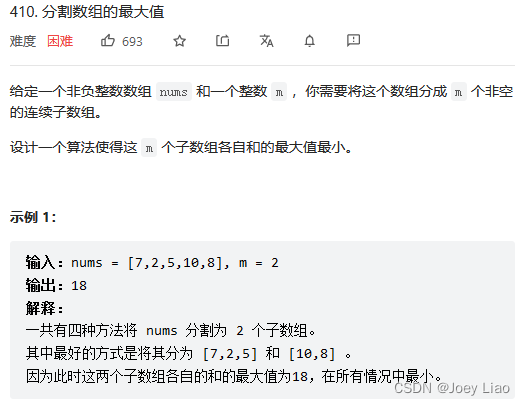
哈哈哈哈哈，发现和第二道题是一模一样的