参数解析

题目描述:
在命令行输入如下命令：
xcopy /s c:\ d:\e，
各个参数如下：
参数1：命令字xcopy
参数2：字符串/s
参数3：字符串c:\
参数4: 字符串d:\e
请编写一个参数解析程序，实现将命令行各个参数解析出来。
解析规则：
1.参数分隔符为空格
2.对于用""包含起来的参数，如果中间有空格，不能解析为多个参数。比如在命令行输入xcopy /s “C:\program files” "d:“时，参数仍然是4个，第3个参数应该是字符串C:\program files，而不是C:\program，注意输出参数时，需要将”"去掉，引号不存在嵌套情况。
3.参数不定长
4.输入由用例保证，不会出现不符合要求的输入
数据范围：字符串长度：1 <= s <= 1000
进阶：时间复杂度：O(n)\O(n) ，空间复杂度：O(n)\O(n)

输入描述:
输入一行字符串,可以有空格
输出描述:
输出参数个数，分解后的参数，每个参数都独占一行

示例:
输入：
xcopy /s c:\ d:\e
输出：
4
xcopy
/s
c:\
d:\e

解题思路

解读题目:就是输入一段字符串,然后先输出有几个参数,在分别输出参数是什么,每一个都要换行

这个题当时我感觉还是有一定的难度,主要就是有双引号的参数不好解析,就是根据空格来划分字符串,其中双引号之间的算一个整体,即使他当中有空格,所以我们重点就要怎们计算双引号之间的字符串,就要先考虑有双引号的情况,两对双引号怎么联系起来,搞清楚了这种情况,这个题还是非常简单的

解题代码

import java.util.*;
public class Main{
    public static void main(String[] args){
        Scanner scan = new Scanner(System.in);
        String str = scan.nextLine();
        int count = 0;
        for(int i = 0;i < str.length();i++){
            //碰到双引号需要寻找下一个双引号
            if(str.charAt(i) == '"'){  
                do{
                    i++;
                }while(str.charAt(i) != '"');
            }
            //参数根据空格来分割
            if(str.charAt(i) == ' '){
                count++;
            }
        }
        //参数个数比除开引号外的空格数多一个
        System.out.println(count + 1);
       int flg = 1;
        for(int i = 0;i < str.length();i++){
            //当遇到第一个引号,让flag 变为 0
            //遇到第二个的时候就会变回来
            if(str.charAt(i) == '"'){
                flg ^= 1;
            }
            //打印除开双引号和特殊空格的字符
            if(str.charAt(i) != ' ' && str.charAt(i) != '"'){
                System.out.print(str.charAt(i));
            }
            //这是在打印双引号中的空格
            if(str.charAt(i) == ' ' && flg == 0){
                System.out.print(str.charAt(i));
            }
            //这是遇到了双引号以外的空格,参数分行
            if(str.charAt(i) == ' ' && flg == 1){
                System.out.println();
            }
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

题链接

参数解析链接

跳石板

题目描述:
小易来到了一条石板路前，每块石板上从1挨着编号为：1、2、3…
这条石板路要根据特殊的规则才能前进：对于小易当前所在的编号为K的 石板，小易单次只能往前跳K的一个约数(不含1和K)步，即跳到K+X(X为K的一个非1和本身的约数)的位置。 小易当前处在编号为N的石板，他想跳到编号恰好为M的石板去，小易想知道最少需要跳跃几次可以到达。
例如：
N = 4，M = 24：
4->6->8->12->18->24
于是小易最少需要跳跃5次，就可以从4号石板跳到24号石板

输入描述:
输入为一行，有两个整数N，M，以空格隔开。 (4 ≤ N ≤ 100000) (N ≤ M ≤ 100000)
输出描述:
输出小易最少需要跳跃的步数,如果不能到达输出-1

示例:
输入:4 24
输出:5

解题思路

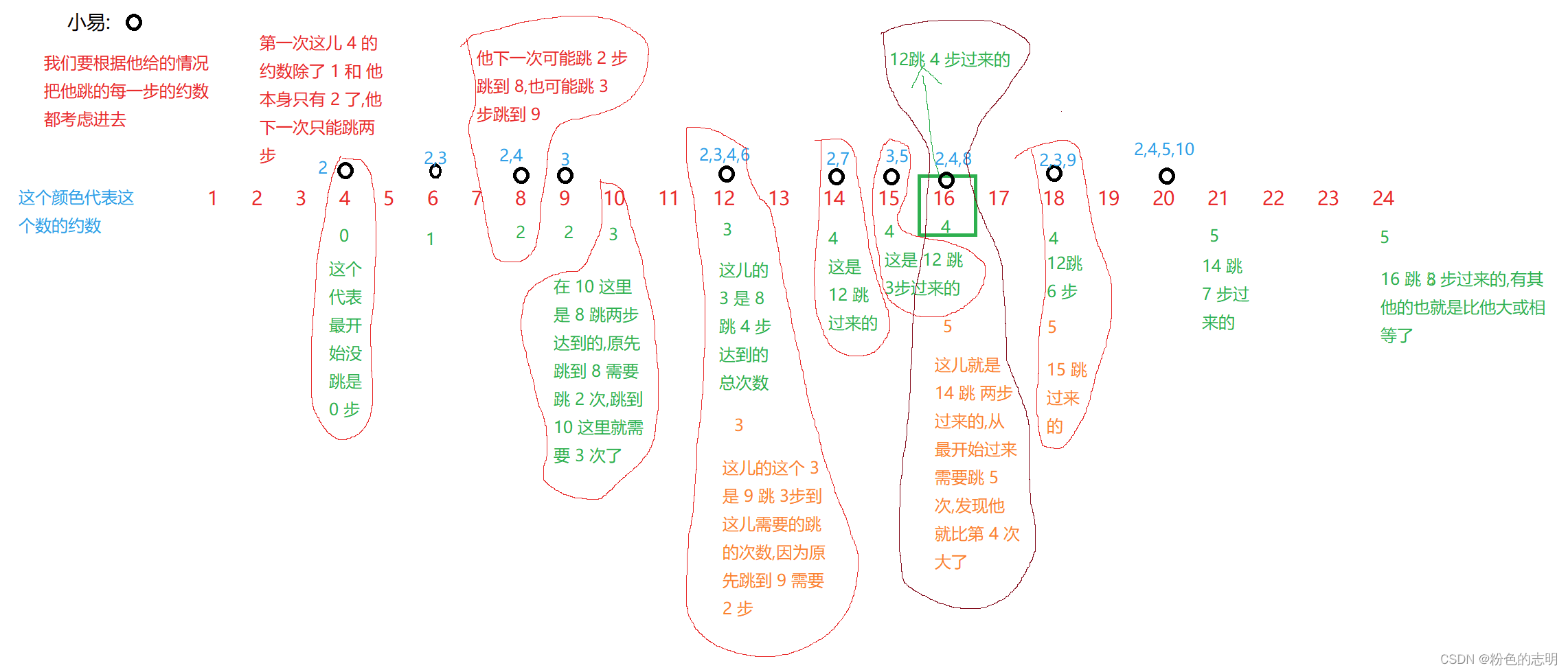
这个题主要就是描述:假设你最开始站在 4 这个位置(你站的数的位置是随机的),你要跳到 24的位置上,但是你每次只能跳除开 1 和 你本身这个数的约数(就是只有 2了,你下次只能跳两步跳到 6上),跳到下一个石板上,对应下一个石板下的数一样的跳这样的约数,跳到24的最小步数,没有就输出 -1…

解题代码

import java.util.*;
public class Main{
    public static void main(String[] args){
        Scanner scan = new Scanner(System.in);
        //最初站的位置
        int n = scan.nextInt();
        //终点位置
        int m = scan.nextInt();
        
        //把跳的次数用这个数组来表示,加一代表跟我们的位置对应,因为数组下标为 0
        int[] step = new int[m + 1];
        for(int i = 0;i < m + 1;i++){
            //先循环把这些都附上最大值,以防我们的次数如果刚好跟上面的值重合了就尴尬了
            step[i] = Integer.MAX_VALUE;
        }
        //在最初的位置上设置为 0 ,代表一步还没跳
        step[n] = 0;
        for(int i = n;i < m;i++){
            //这个位置上的值没变化,代表跳过了这个石板的,就不需要在执行下面的代码了,直接 遍历下一个 (i++)
            if(step[i] == Integer.MAX_VALUE){
                continue;
            }
            
            //用集合把该石板的约数记下来
            List<Integer> list = div(i);
            for(int j : list){
                //第一个条件表示还没跳到最终位置,第二个条件表示跳的这个位置已经被别个跳过了
                if(i + j <= m && step[i + j] != Integer.MAX_VALUE){
                    //记录最小的一个的跳的次数
                    step[i + j] = Math.min(step[i + j],step[i] + 1);
                    //还没被别个跳到过这里
                }else if(i + j <= m){
                    //跳的次数 加一
                    step[i + j] = step[i] + 1;
                }
            }     
        }
        //如果最终位置都还没被计数说明根被就没有跳到过这里
        if(step[m] == Integer.MAX_VALUE){
            System.out.println(-1);
        }else{
            //跳到最终位置的最小次数
            System.out.println(step[m]);
        }
    }
    
    //约数方法
    public static List<Integer> div(int num){
        List<Integer> list = new ArrayList<>();
        for(int i = 2;i * i <= num;i++){
            if(num % i == 0){
                list.add(i);
                if(num / i != i){
                    list.add(num / i);
                }
            }
        }
        return list;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

题链接

跳石板链接