深度学习

文章代码原文链接

https://gitee.com/fakerlove/deep-learning
1

学习路线

1-----python

2----常见的深度学习框架

3-----pytorch学习

4----CV领域学习

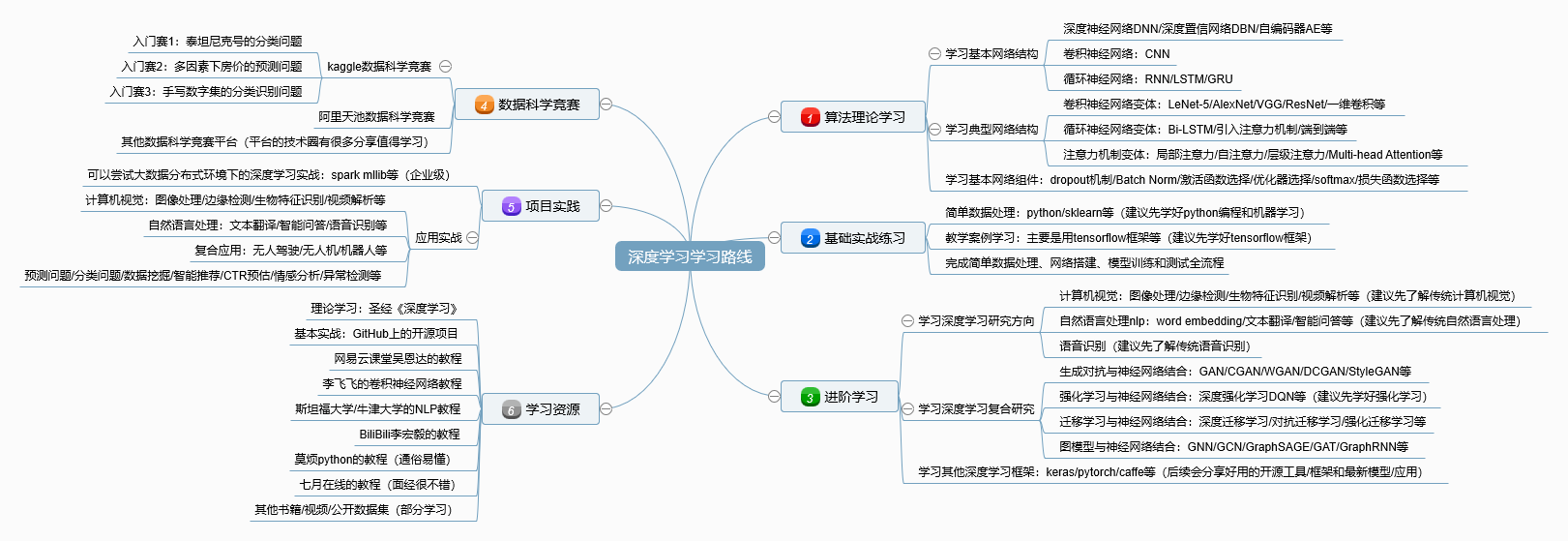
0. 概述

0.1 概念

很多人都有误解，以为深度学习比机器学习先进。其实深度学习是机器学习的一个分支。

可以理解为具有多层结构的模型。具体的话，深度学习是机器学习中的具有深层结构的神经网络算法，即机器学习>神经网络算法>深度神经网络（深度学习）。

深度学习（deep learning，以下简称DL），换种说法，可以说是基于人工神经网络的机器学习。区别于传统的机器学习，DL需要更多样本，换来更少的人工标注和更高的准确率。

传统的BP神经网络一般指三层的全连接神经网络，而大于三层就成了DNN（深度神经网络）。

事实上，DNN能解决一些问题，但因为参数太多，逐步被其他网络模型取代：CNN（卷积神经网络）、RNN（循环神经网络）。二者目前最成功的实现分别是ResNet和LSTM。

深度学习三巨头

• 神经网络之父hinton
• 卷积神经网络之父lecun
• GAN网络之父bengio

LSTM 之父 Jürgen Schmidhuber

0.2 历史

• 第一代神经网络又称为感知器，由科学家Frank Rosenblatt发明于1950至1960年代，它的算法只有两层，输入层输出层，，主要使用的是一种叫做sigmoid神经元（sigmoid neuron）的神经元模型，主要是线性结构。它不能解决线性不可分的问题，如异或操作。
• 为了解决第一代神经网络的缺陷，在1980年左右提出第二代神经网络多层感知器（MLP）。和第一代神经网络相比，第二代在输入输出层之间有增加了隐含层的感知机，引入一些非线性的结构，解决了之前无法模拟异或逻辑的缺陷。第二代神经网络让科学家们发现神经网络的层数直接决定了它对现实的表达能力，但是随着层数的增加，优化函数愈发容易出现局部最优解的现象，由于存在梯度消失的问题，深层网络往往难以训练，效果还不如浅层网络。
• 2006年Hinton采取无监督预训练（Pre-Training）的方法解决了梯度消失的问题，使得深度神经网络变得可训练，将隐含层发展到7层，有一个预训练的过程。使用微调技术作为反向传播和调优手段。减少了网络训练时间，并且提出了一个新的概念叫做"深度学习"，直到2012年，在ImageNet竞赛中，Hinton教授的团队，使用以卷积神经网络为基础的深度学习方案，他们训练的模型面对15万张测试图像时，预测的头五个类别的错误率只有 15.3%，而排名第二的日本团队，使用的SVM方法构建的模型，相应的错误率则高达 26.2%。从此一战成名！2012年后深度学习就成为主流。

1. 感知机

资料参考

https://blog.csdn.net/m0_37957160/article/details/113922919
1

资料参考2

https://blog.csdn.net/Insincerity/article/details/106446689
1

资料参考3

https://www.jianshu.com/p/81fa7682daf3
1

1.1 概念

感知机是1957年，由Rosenblatt提出会，是神经网络和支持向量机的基础。

感知机是二分类的线性分类模型，输入为实例的特征向量，输出为实例的类别（取+1和-1）。感知机对应于输入空间中将实例划分为两类的分离超平面。感知机旨在求出该超平面，为求得超平面导入了基于误分类的损失函数，利用梯度下降法对损失函数进行最优化。

1.2 算法模型

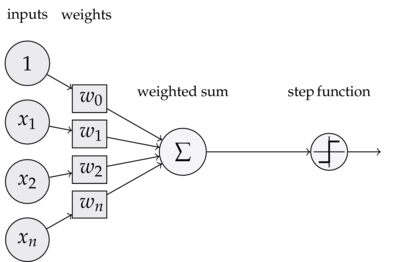
1.2.1 模型

输入:$x\in R^n$，x是特征向量​​

输出: Y ∈ { − 1 , 1 } Y\in \{-1,1\} Y∈{−1,1}

由输入空间到输出空间的表达形式为：

$y=sign(w\times x+b)$​

上面该函数称为感知机，其中w，b称为模型的参数，$w\in R^n$称为权值，b称为偏置，$w\times x$表示为w，x的内积
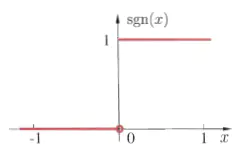
f ( n ) = { 1 , i f n ≥ 0 0 , o t h e r w i s e f(n)={1,ifn≥00,otherwise

f(n)={1,ifn≥00,otherwise​

下面是符号函数的函数图像(w为一维的数据量$w=[w_1]$​)：

1.2.2 分离超平面

感知机的作用就是找到一个分离超平面，使数据能够正确分为两类。

在实际情况中，w往往是 w = [ w 1 w 2 ⋮ w n ] w=[w1w2⋮wn]

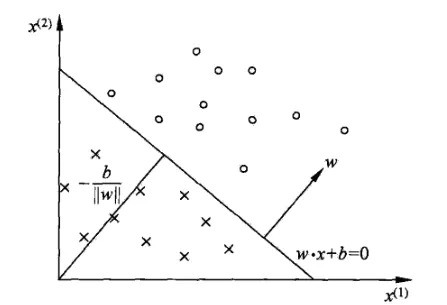
w=⎣⎢⎢⎢⎡​w1​w2​⋮wn​​⎦⎥⎥⎥⎤​​，多维的。这个时候$w\times x+b$​表示的是超平面​​

在感知机中，一般把超平面方程写为：wx+b=0.

w 为超平面的法向量，b 是超平面的截距，超平面把数据分为两类，如下图。

1.2.3 损失函数

感知机能够自动地把 w 和 b 求解出来，求解过程中有个重点，就是损失函数的引入，损失函数也叫代价函数，是样本分类预测结果和样本实际类别差异的度量，正是通过最小化损失函数，感知机才能不断地修正w和b的值，找到一个最优的超平面。

1. 超平面的距离

感知机中的损失函数是所有误分类点到分离超平面的距离，其中，某一个误分类点到超平面的距离表示为：

$\frac{1}{||w||}|w\cdot x_0+b|$

$||w||$是$w$的$L_2$范数，这个L2范数乍听有点高大上，实际上就是 w 中每个元素去平方，然后相加开根号

$||w||=\sqrt{w_1^2+w_2^2+\cdots +w_n^2}$​

2. 误分类点到分离超平面的距离

对于一个误分类数据$(x_i,y_i)$​​，当 $w\cdot x_i+b>0$​​ 时,$y_i=-1$​​;当$w\cdot x_i+b<0$​​时，$y_i=1$​​;所以$y_i\ast (w\cdot x_i+b)>0$​​​，所有误分类点到分离超平面的距离为：

$-\frac{1}{||w||}{\sum }_{x_i\in M}{y}_i(w\cdot x_i+b),M是误分类集合$​​

为啥距离是这个呢？？？,

$因为y_i=1或-1,不改变结果，只改变正负$

不考虑$\frac{1}{||w||}$损失函数写成这样：

$L(w,b)=-{\sum }_{x_i\in M}{y}_i(w\cdot x_i+b)$

我们的目标就是最小化损失函数 L(w,b)，这里用 **随机梯度下降（SGD）**的方法来做最小化。

L0范数是指向量中非0的元素的个数。(L0范数很难优化求解)

L1范数是指向量中各个元素绝对值之和

L2范数是指向量各元素的平方和然后求平方根

1.2.4 随机梯度下降

梯度下降方向就是梯度的反方向，最小化损失函数 L(w,b) 就是先求函数在 w 和 b 两个变量轴上的偏导：

${\nabla }_{w}L(w,b)=-{\sum }_{x_i\in M}{y}_i{x}_i$

${\nabla }_{b}L(w,b)=-{\sum }_{x_i\in M}{y}_i$

上面的式子，每更新一次参数，需要遍历整个数据集，如果数据集非常大的话，显然是不合适的，为了解决这个问题，只随机选取一个误分类点进行参数更新，这就是随机梯度下降（SGD），如下所示。

$w+\eta y_i{x}_i\to w$

$b+\eta y_i\to b$

这里的 η 指的是学习率，相当于控制下山的步幅，$\eta$ 太小，函数拟合（收敛）过程会很慢，$\eta$太大，容易在最低点方向震荡，进入死循环。

当没有误分类点的时候，停止参数更新，所得的参数就是感知机学习的结果，这就是感知机的原始形式。下面总结一下参数更新的过程：
（1）预先设定一个$w_0$​和$b_0$​，即w和b的初值。
（2）在训练集中选取数据$(x_i,y_i)$​。
（3）当$y_i\ast (w\cdot x_i+b)\le 0$​​时，利用随机梯度下降算法进行参数更新。

例子

输入：正例$x_1=[3,3{]}^T,x_2=[4,3{]}^T,负例x_3=[1,1{]}^T。$

输出:感知机模型$f(x)=sign(w\times x+b)$

目标公式$mi{n}_{w,b}=-{\sum }_{x_i\in M}{y}_i(w\cdot x+b)$​

• 假设 w 0 = [ 0 0 ] , η = 1 , b 0 = 0 w_0=[00]

  ,\eta=1,b_0=0 w0​=[0​0​],η=1,b0​=0​

• 判断$x_1$​是否正确分类， y 1 ( w 0 ⋅ x 1 + b ) = [ 0 0 ] [ 3 3 ] + 0 = 0 y_1(w_0\cdot x_1+b)=[00]

  [33]
  +0=0 y1​(w0​⋅x1​+b)=[0​0​][33​]+0=0不能正确分类

  更新$w,b$​

• 更新公式为$w+\eta y_i{x}_i\to w$

  w 1 = w 0 + η y 1 x 1 = [ 0 0 ] + 1 × 1 × [ 0 0 ] = [ 3 3 ] w_1=w_0+\eta y_1x_1=[00]

  +1\times 1\times [00]
  =[33]
  w1​=w0​+ηy1​x1​=[0​0​]+1×1×[0​0​]=[3​3​]​

  同理$b_1=b_0+y_1=1$,得到新的模型$w_1\cdot x+b_1$

• 更新后的模型，对于$x_1,x_2$​被正确分类​，但是对于$x_3$错误分类。进行更新$w_1,b_1$​

  w 2 = w 1 + η y 3 x 3 = [ 0 0 ] + 1 × ( − 1 ) × [ 1 1 ] = [ 2 2 ] w_2=w_1+\eta y_3x_3=[00]

  +1\times (-1)\times [11]
  =[22]
  w2​=w1​+ηy3​x3​=[0​0​]+1×(−1)×[1​1​]=[2​2​]$b_2=0$

依次类推

迭代过程如下

1.2.5 对偶形式

将 w 和 b 表示为实例$x_1$和标记$y_1$线性组合的形式，通过求解系数来求解w和b，前面提到过这个式子：

$w+\eta y_i{x}_i\to w$

$b+\eta y_i\to b$

这里先假设 w 和 b 的初值为0，那么通过对偶形式能表示为什么？从上面式子可以看出来，每次迭代，w会增加一个 $\eta y_i{x}_i$，b 会增加一个$\eta y_i$，到最后参数更新完之后，w 和 b 一共增加了这些：

$w={\sum }_{i=1}^N{\alpha }_i{y}_i{x}_i$

$b={\sum }_{i=1}^N{\alpha }_i{y}_i$

这里的${\alpha }_i=n_i\ast \eta$，$n_i$就是$(x_i,y_i)$​被误分类的次数，η 还是学习率。

${\alpha }_i$越大，意味这实例点更新次数越多，距离分离超平面越近，越难被分类，对实例影响结果越大​

下面是对偶形式的参数更新过程：

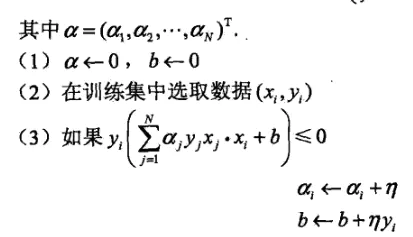
1.3 逻辑电路

1.3.1 与门

1.3.2 与非门

1.3.3 或门

1.3.4 异或门

什么是异或？就是，假如这里有两件事，一真一假，异或为真；两件事都为假或者两件事都为真，异或为假，就像这样：
0⊕0=0,0⊕1=1
1⊕0=1,1⊕1=0
下面是异或的函数图像：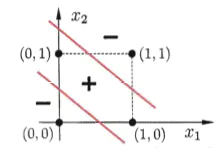

通过图像可以看出，找不到一个超平面能将这四个点分隔开，所以感知机无法处理异或问题，不仅仅是感知机，其他线性模型也无法处理这种问题。

多层感知机mlp

如何解决呢？？？

使用多层的感知机即可完成，如下图所示

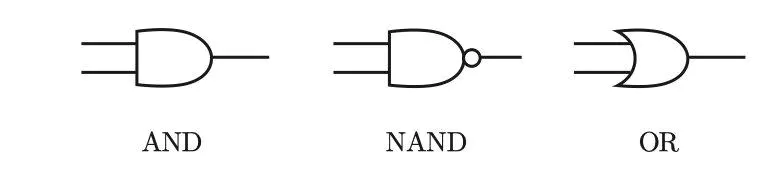
与门、与非门、或门的符号

通过上面的感知机如何组成异或门呢？？

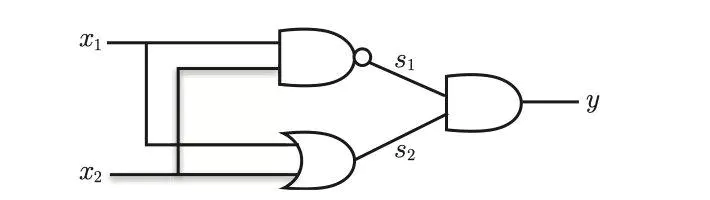
这里，把$s_1$作为 与非门 的输出，把$s_2$ 作为或门的输出，填入真值表中。

结果如图所示，观察$x_1、x_2、y$，可以发现确实符合异或门的输出

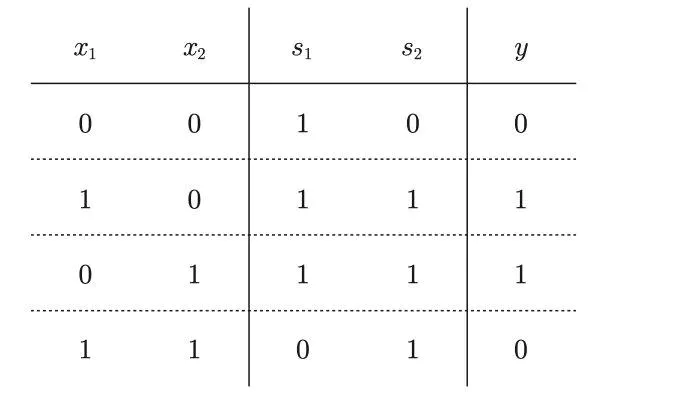
异或门是一种多层结构的神经网络。

与门、或门是单层感知机，而异或门是2层感知机。叠加了多 层的感知机也称为多层感知机（multi-layered perceptron） 。

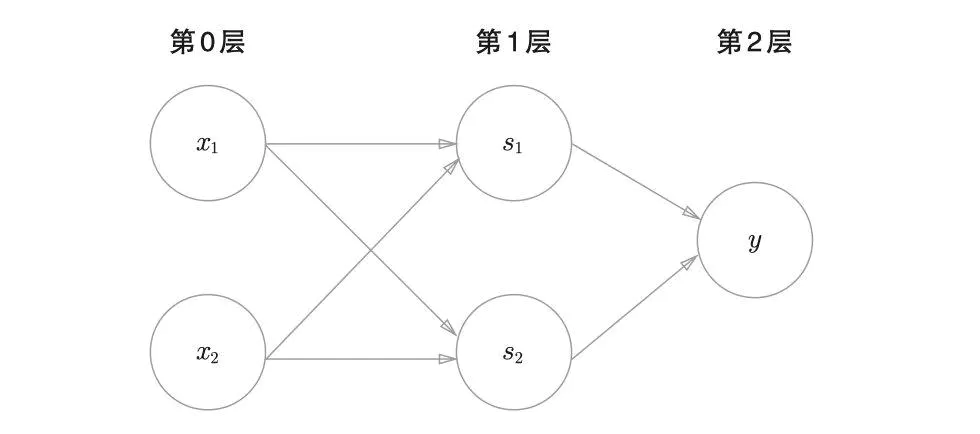
感知机的作用就是引出神经网络