欢迎来到对抗路——机器学习-多元线性回归模型（详解）

🍌文章适合于所有的相关人士进行学习🍌
🍋各位看官看完了之后不要立刻转身呀🍋
🍑期待三连关注小小博主加收藏🍑
🍉小小博主回关快 会给你意想不到的惊喜呀🍉

---

🐲前言

上次博客我们讲解了关于一元线性回归模型的知识一元线性回归模型，对于一元线性回归模型来说，其反应的是单个自变量对于因变量的影响，但是在实际生活中一般影响因变量的因素往往不止一个，比如说我们相亲的时候，往往会看重对方的经济基础、外貌、有房无房、等等因素。从而我们需要将一元线性回归模型拓展到多元线性回归模型。

🐲多元线性回归模型讲解

🐮公式推导

其中x ij表示第i行的第j个自变量，如果按照一元线性回归模型的逻辑，那么多元线性回归模型应该就是因变量y和自变量X的线性结合。
所以基于一元线性回归模型，我们可以把多元线性回归模型表示为：

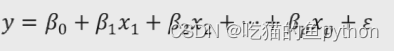
根据我们线性代数学过的知识，可以将其表示为：

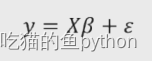
还是按照我们一元线性回归模型的推导，就是误差项如果越小，是不是就说明我们这条拟合线拟合的就越好！
所以我们继续进行推导：

这里我们就推导完成了！

🐮案例

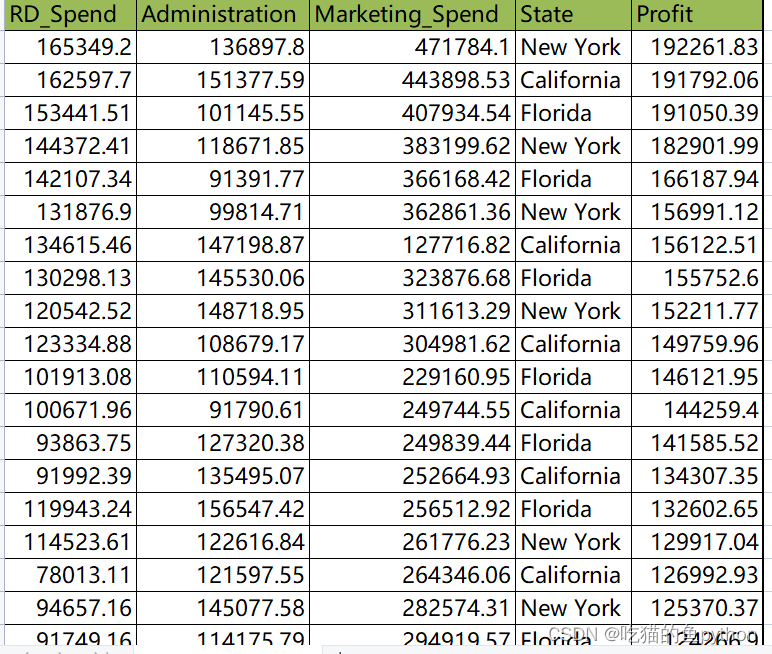
这里为研发成本、管理成本、市场营销、地区和利润的关系。
我们想要看看前面这四列到底和利润中间存在不存在线性关系，怎么判断存不存在线性关系？

🐮案例解决代码

这里我们依旧使用anaconda中的jupyter notebook来讲解。
这里我们进行一下说明，这里model_selection这个库是将数据集分为训练集和测试集，比如说一个数据一半分为训练集，一般分为测试集，那么训练集的作用是通过训练来得到参数，测试集是得到参数之后看看最终预测结果的预测值和实际值进行比较。

from sklearn import model_selection
import pandas as pd
import statsmodels.api as sm
Profit=pd.read_excel(r'Predict to Profit.xlsx')
train,text=model_selection.train_test_split(Profit,test_size=0.2,random_state=1234)
#这里进行说明Profit就是数据，从该数据中进行分集合，测试集为20%，
#后面这个表示如果选出来就固定这个选法，以后也不会变。如果为0，
#就是每次分的测试集和训练集是变化的，是不一样的。
model=sm.formula.ols('Profit ~ RD_Spend+Administration+Marketing_Spend+C(State)'，data=train).fit()
#对训练集进行拟合
print(model.params)#参数
text_X=test.drop(labels='Profit',axis=1)#删除测试集合中的profit列
pred=model.predict(exog=text_X)#对测试集合进行预测
print(pd.DataFrame(pred,test.Profit))
1
2
3
4
5
6
7
8
9
10
11
12
13
14

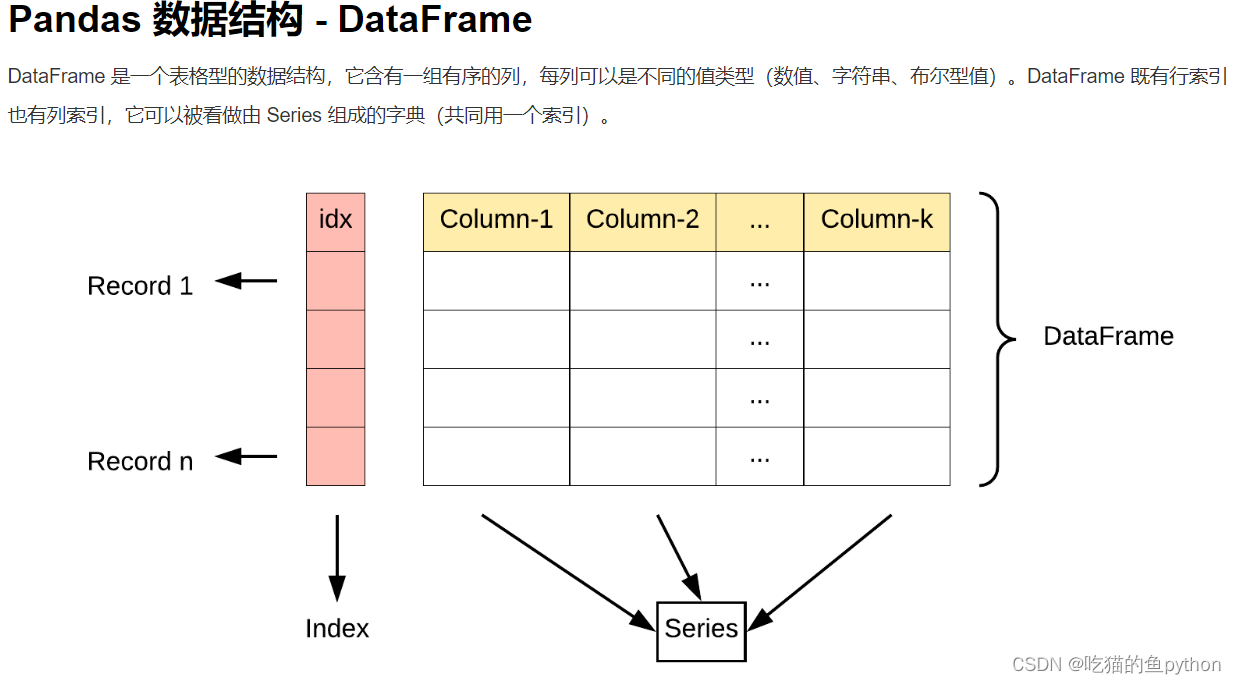
也就是说，pd.DataFrame相当于建立一个表格。
最后我们输出的结果是

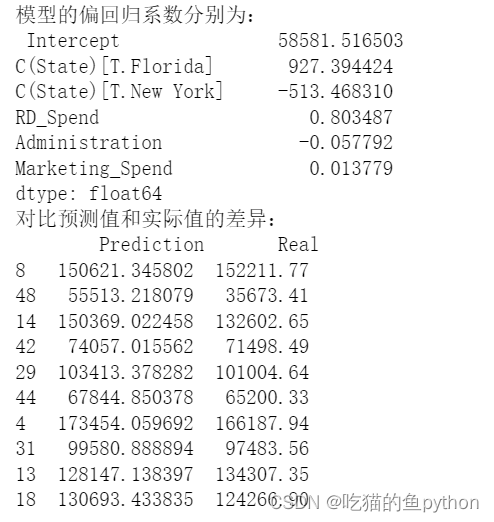
默认情况下，对于离散变量State而言，模型选择California值作为对照组。

🐮数据哑变量处理

当我们看到数据时，看到了研发成本等数字类型数据可以进行分析，那么文字类型的怎么处理呢？也不能说使用文字内容来作为因变量吧，所以我们引入了一个新的内容就是哑变量。
什么叫哑变量呢？？这里我们介绍一个例子来看

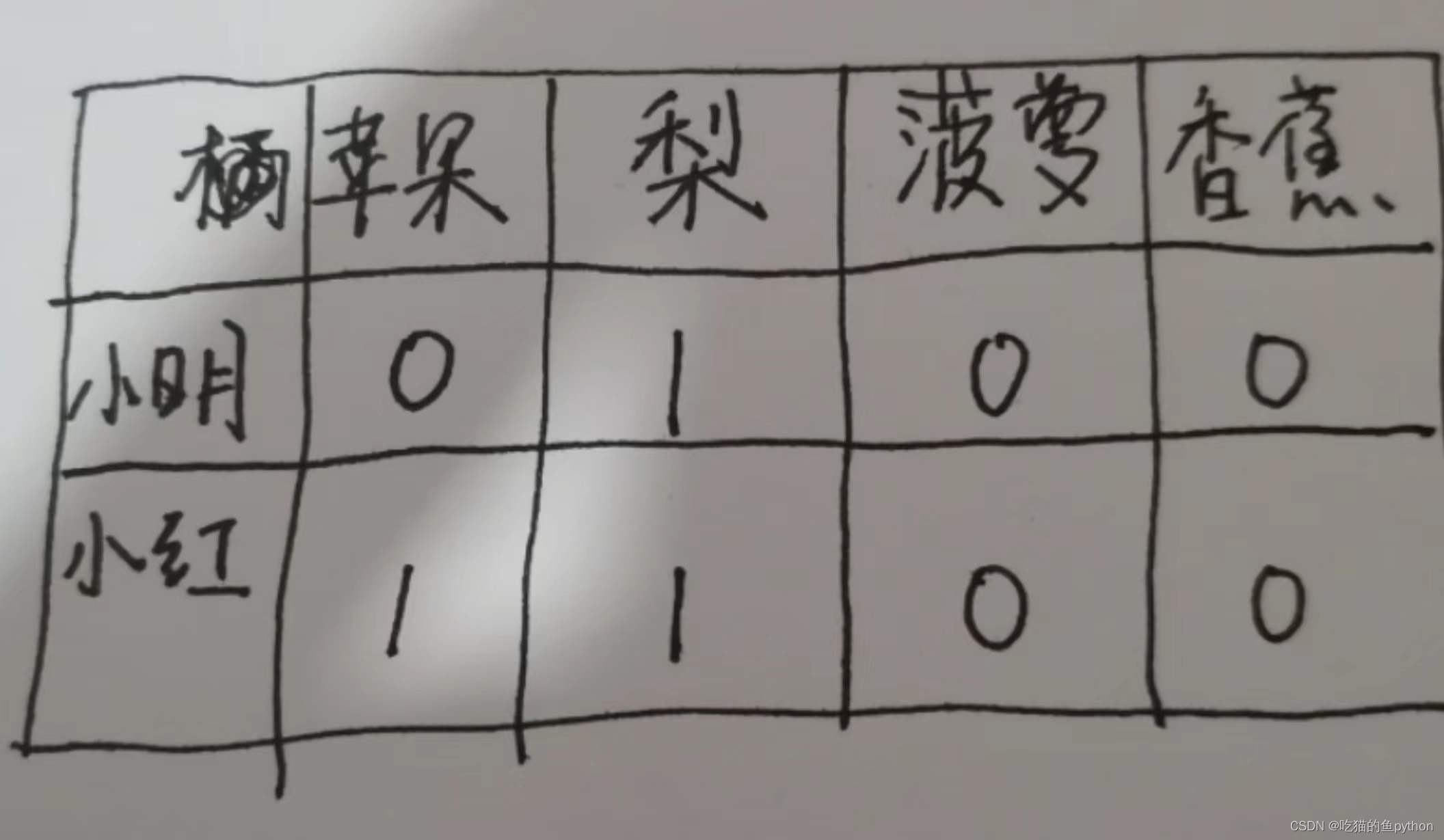
这里就表示小明买了梨。小红买了苹果还有梨。但是我们按照上图这种形式来表示就是哑变量处理。
然后我们对State进行哑变量处理。

dummies=pd.get_dummies(Profit.State)
#将数据State进行哑变量处理
Profit_New=pd.concat([Profit,dummies],axis=1)
#和原始数据进行拼接
Profit_New.drop(labels=['State','New York'],axis=1,inplace=True)
#删除'State','New York'，以'New York'作为对比
train,test=model.selection.train_test_split(Profit_New,test_size=0.2,random_state=1234)
#同上道理
model2=sm.formula.ols('Profit ~ RD_Spend+Administration+Marketing_Spend+Florida+California'，data=train).fit()
print(model2.params)#输出偏回归系数
1
2
3
4
5
6
7
8
9
10

结果是：

🐮如何判断是否线性相关

🐺模型的F检验

1. 提出问题的原假设和备择假设
2. 在原假设的条件下，构造统计量F
3. 根据样本信息，计算统计量的值
4. 对比统计量的值和理论F分布的值，当统计量值超过理论值时，拒绝原假设，否则接受原假设

🐷提出假设

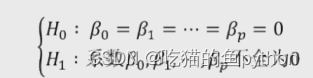
🐷构造统计量F

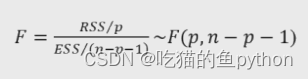
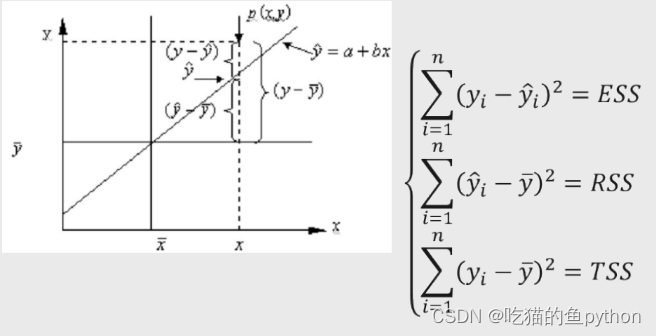
其中RSS和ESS以及TSS分别表示：
ESS表示误差平方和，衡量是因变量的实际数值和预测值之间的离差平方和，会随着模型的变化而变动。
RSS表示为回归离差平方和，衡量是因变量的预测值与实际均值之间的离差平方和。同样会随着模型的变化而变化。
TSS为总的离差平方和，衡量是因变量的值和其均值之间的离差平方和。不会随着模型的变化而变化，是一个固定值。
其中TSS=ESS+RSS
ESS的降低会导致RSS的升高，所以当ESS的数值达到最小的时候，那么RSS就会达到最大。按照这个逻辑，可以构造F统计量。

🐷计算统计量代码

import numpy as np
# 计算建模数据中因变量的均值
ybar = train.Profit.mean()
# 统计变量个数和观测个数
p = model2.df_model
n = train.shape[0]
# 计算回归离差平方和
RSS = np.sum((model2.fittedvalues-ybar) ** 2)
import numpy as np
# 计算建模数据中因变量的均值
ybar = train.Profit.mean()
# 统计变量个数和观测个数
p = model2.df_model
n = train.shape[0]
# 计算回归离差平方和
RSS = np.sum((model2.fittedvalues-ybar) ** 2)
# 计算误差平方和
ESS = np.sum(model2.resid ** 2)
# 计算F统计量的值
F = (RSS/p)/(ESS/(n-p-1))
print('F统计量的值：',F)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

结果为174.6

🐷对比结果

from scipy.stats import f
# 计算F分布的理论值
F_Theroy = f.ppf(q=0.95, dfn = p,dfd = n-p-1)
print('F分布的理论值为：',F_Theroy)
1
2
3
4

结果为2.5
所以我们得出结论，原假设不成立。即认为多元线性回归模型是显著的，也就是说回归模型的偏回归系数都不全为0。那么究竟哪个对最终的利润有关呢？这就用到了t检验

🐺模型的t检验

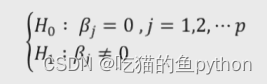
按照同上步骤操作。
然后我们最后进行模型的概览

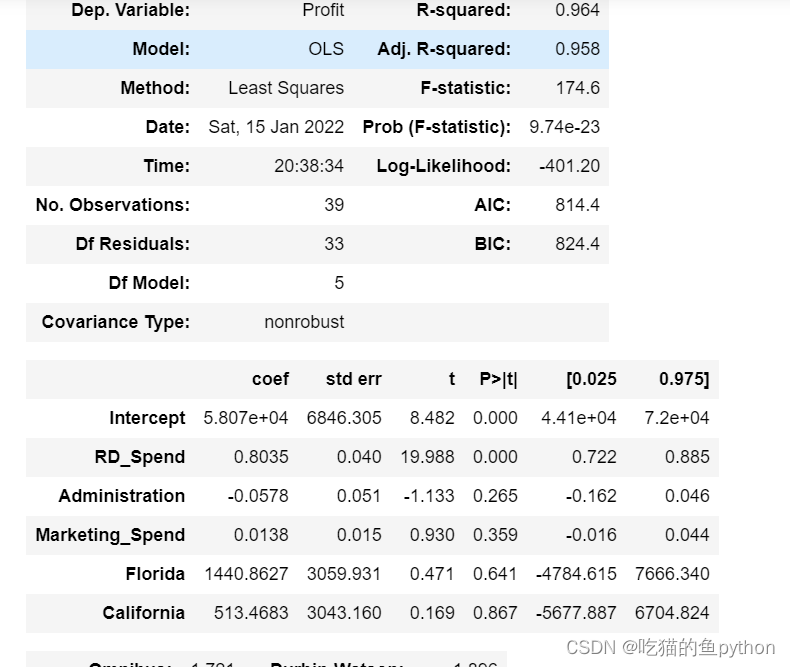
这里只有前面两项p值小于0.05，说明了通过了系数的显著性检验，其他变量和利润的关系就很小了。
那么这样我们今天的内容就结束了！！！大佬们慢慢消化这段内容。谢谢各位的观看