一、坐标系概述

        在几何学中，坐标系是使用一个或多个数字或坐标来唯一确定点或其他几何元素在诸如欧几里得空间的流形上的位置的系统。坐标的顺序很重要，它们有时通过它们在有序元组中的位置来标识，有时通过字母标识，如“ x坐标”。坐标在初等数学中被视为实数，但可能是复数或更抽象系统的元素，例如交换环。使用坐标系可以将几何问题转化为数字问题，反之亦然；这是解析几何的基础。

        我们大多数人都熟悉笛卡尔坐标系，并在绘制点和绘制方程时使用它。但是还有许多其他坐标系被广泛应用于数学和其他领域。

1、数轴

        坐标系的最简单示例是使用数轴识别具有实数的线上的点。在该系统中，在给定线上选择任意点O（原点）。点P的坐标定义为从O到P的有符号距离，其中有符号距离是根据线P位于哪一侧而取为正或负的距离。每个点都有一个唯一的坐标，每个实数是一个唯一点的坐标。

        在数轴上写下点让我们很容易比较它们。数轴由三个部分组成——负边、零和正边。0左边的点是负数，0右边的点都是正数。

2、笛卡尔坐标系

（1）平面笛卡尔坐标系

        笛卡尔坐标系中的笛卡尔坐标是根据x坐标轴和y坐标轴指定的，如下图所示。原点是x轴和y轴的交点。平面中一点的笛卡尔坐标写为 ( x , y )。第一个数字x称为x坐标（或x分量），因为它是沿x轴方向到原点的有符号距离。

        在笛卡尔坐标系中，x坐标指定到y轴右侧（如果x为正）或左侧（如果 x 为负）的距离。类似地，第二个数字y称为y坐标（或y分量），因为它是沿y轴方向到原点的有符号距离。y坐标指定 x 轴上方（如果y为正）或下方（如果y为负）的距离。在下图中，该点具有坐标 (-3, 2)，因为该点向左三个单位，从原点向上两个单位。

（2）三维空间中的笛卡尔坐标

        在三维空间中，笛卡尔坐标系基于三个相互垂直的坐标轴：x轴、y轴和z轴。三轴相交于称为原点的点。您可以想象原点是房间角落的墙壁与地板相交的点。

        三维笛卡尔坐标系中一个点的笛卡尔坐标是一个三元组的数字 ( x , y , z )。这三个数字或坐标分别指定沿x、y和z 轴到原点的有符号距离。它们可以通过形成具有平行于坐标轴的边缘以及在原点和给定点的对角的框来可视化。三维笛卡尔坐标系中点的笛卡尔坐标 ( x , y , z ) 与x、y和z轴分别。

3、极坐标系

        极坐标系是一种二维坐标系，其中平面上的每个点由与参考点的距离和与参考方向的角度确定。当我们考虑在平面上绘制点时，我们通常会想到笛卡尔坐标系中的直角坐标 ( x , y )。但是，还有其他编写坐标对和其他类型网格系统的方法。极坐标是标记为 ( r , 𝛳) 并绘制在极坐标网格上的点。极坐标网格表示为从极点或坐标平面原点向外辐射的一系列同心圆。

        参考点（类似于笛卡尔坐标系的原点）称为极点，从极点沿参考方向发出的射线称为极轴。距极点的距离称为径向坐标或半径，角度称为角坐标、极角或方位角。径向坐标通常用r或 ⍴ 表示，角坐标用 𝛳、ɸ 或t表示。

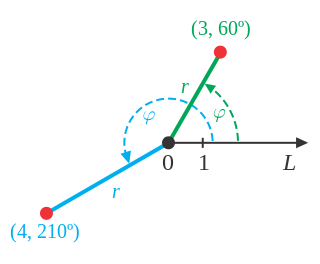
        极坐标中的角度通常以度或弧度表示（2π = 360 o）。度数传统上用于导航、测量和许多应用学科，而弧度在数学和数学物理中更为常见。在许多情况下，正角坐标意味着角度 φ 是从轴逆时针测量的。在数学文献中，极轴通常水平绘制并指向右侧。 

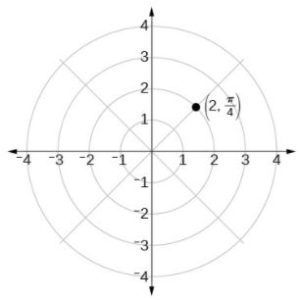
        使用极坐标绘制点

        极坐标网格被缩放为单位圆，现在将正 x 轴视为极轴，将原点视为极点。第一个坐标r是从极点开始的有向线段的半径或长度。以弧度测量的角度 𝛳 表示r的方向。我们从极轴逆时针移动一个角度 𝛳。即使我们先测量 𝛳 再测量r，极点还是先用 r 坐标写入。例如，要绘制点 (2, π/4)，我们将沿逆时针方向移动 π/4 个单位，然后距离极点的长度为 2。

4、齐次坐标系

        齐次坐标或射影坐标，由 August Ferdinand Möbius 在其 1827 年的著作Der barycentrische Calcul中介绍，是射影几何中使用的坐标系统，就像在欧几里得几何中使用笛卡尔坐标一样。它们的优点是可以使用有限坐标表示点的坐标，包括无穷远处的点。涉及齐次坐标的公式通常比它们的笛卡尔坐标系对应物更简单、更对称。齐次坐标具有一系列应用，包括计算机图形学和 3D 计算机视觉，它们允许仿射变换，一般来说，投影变换可以很容易地用矩阵表示。

        如果一个点的齐次坐标乘以一个非零标量，那么得到的坐标代表同一个点。由于齐次坐标也被赋予无限远的点，因此允许这种扩展所需的坐标数比所考虑的投影空间的维数大一。例如，需要两个齐次坐标来指定投影线上的一个点，而需要三个齐次坐标来指定投影平面上的一个点。

        真正的射影平面可以被认为是添加了额外点的欧几里得平面，这些点被称为无穷远点，并且被认为位于一条新线上，即无穷远线。每个方向都有一个无穷远点（数值由直线的斜率给出），非正式地定义为沿该方向远离原点的点的极限。欧几里得平面中的平行线相交于无限远的一点，对应于它们的共同方向。

        给定欧几里得平面上的一个点 ( x , y )，对于任何非零实数Z，三元组 ( xZ , yZ , Z ) 称为该点的一组齐次坐标。根据这个定义，将三个齐次坐标乘以一个共同的非零因子可以为同一点提供一组新的齐次坐标。

        特别是，( x , y , 1) 是点 ( x , y ) 的齐次坐标系。例如，笛卡尔点 (1, 2) 可以在齐次坐标中表示为 (1, 2, 1) 或 (2, 4, 2)。通过将前两个位置除以第三个位置来恢复笛卡尔坐标系中的原始坐标。因此，与笛卡尔坐标不同，一个点可以由无限多个齐次坐标表示。

        通过原点 (0, 0) 的直线方程可以写成nx + my = 0，其中n和m不都是 0。在参数形式中，这可以写成x = mt , y = - nt。令Z = 1/ t，因此线上一点的坐标可以写成 ( m / Z , − n / Z )。在齐次坐标中，这变为 ( m , − n , Z )。

        在极限中，随着t接近无穷大，即随着点远离原点，Z接近 0，该点的齐次坐标变为 ( m , − n , 0)。因此，我们将 ( m , − n , 0) 定义为无穷远点的齐次坐标，对应于线nx + my = 0 的方向。就像欧几里德平面的任何线平行于通过原点的线一样，由于平行线在无穷远处有同一个点，所以欧几里得平面每条线上的无穷大点都被赋予齐次坐标。

        关于齐次坐标系的要点是：

        投影平面中的任何点都由三元组（X、Y、Z）表示，称为该点的齐次坐标或射影坐标，其中X、Y和Z 不全为 0。
        如果坐标乘以一个公因子，则由一组给定齐次坐标表示的点不变。
        相反，当且仅当通过将所有坐标乘以相同的非零常数从另一组获得一组齐次坐标时，才表示同一点。
        当Z不为 0 时，表示的点是欧几里得平面中的点 ( X/Z , Y/Z )。
        当Z为 0 时，表示的点是无穷远处的点。

5、曲线坐标系

        曲线坐标系是欧几里得空间的坐标系，其中坐标线可能是弯曲的。这些坐标可以通过在每个点使用局部可逆的变换（一对一映射）从一组笛卡尔坐标导出。这意味着可以将笛卡尔坐标系中给定的点转换为其曲线坐标并返回。曲线坐标这个名称由法国数学家拉梅创造，源于曲线系统的坐标表面是弯曲的这一事实。

        三维欧几里得空间 ( 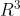) 中曲线坐标系的著名示例是柱坐标和球坐标。

        该空间中的笛卡尔坐标面是坐标平面；例如，z = 0 定义x – y平面。在同一空间中，球坐标中的坐标面r =1 是单位球面的曲面，它是弯曲的。曲线坐标的形式提供了标准坐标系的统一和一般描述。

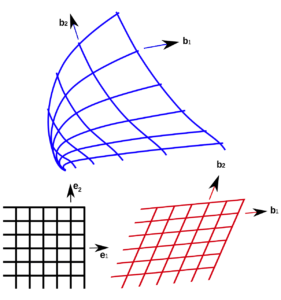
        曲线坐标通常用于定义物理量的位置或分布，例如，标量、向量或张量。根据标量、向量和张量的转换规则，向量微积分和张量分析中涉及这些量的数学表达式（例如梯度、散度、旋度和拉普拉斯算子）可以从一个坐标系转换到另一个坐标系。然后，这样的表达式对任何曲线坐标系都有效。

        对于某些应用，曲线坐标系可能比笛卡尔坐标系更易于使用。受中心力影响的粒子运动在球坐标系中通常比在笛卡尔坐标系中更容易求解；这对于在R 3中定义的许多具有球对称性的物理问题都是正确的。具有遵循特定曲线坐标系的坐标表面的边界条件的方程可能更容易在该系统中求解。

        虽然人们可能会使用笛卡尔坐标来描述矩形框中粒子的运动，但球体中的运动更容易使用球坐标。球坐标是最常见的曲线坐标系，用于地球科学、制图学、量子力学、相对论和工程学。

6、对数极坐标系

        对数极坐标（或对数极坐标）是二维坐标系，其中一个点由两个数字标识，一个为到某一点的距离的对数，一个为角度。对数极坐标与极坐标密切相关，极坐标通常用于描述平面中具有某种旋转对称性的域。在谐波和复分析等领域，对数极坐标比极坐标更规范。

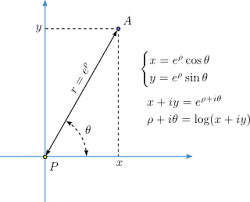
        平面中的对数极坐标由一对实数 组成，其中 ρ 是给定点与原点之间距离的对数，θ 是参考线之间的角度（x轴) 和通过原点和点的线。

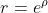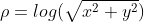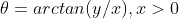        角坐标与极坐标相同，而径向坐标根据规则进行变换，其中 r 是到原点的距离。从笛卡尔坐标转换到对数极坐标的公式由 和 给出。

        从对数极坐标到笛卡尔坐标的转换公式是 和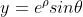

        通过使用复数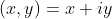，变换可以写成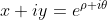

7、重心坐标系

        在几何学中，重心坐标系是一种坐标系，其中点的位置通过参考单纯形（平面中的点用三角形，三维空间中的点用四面体等）来指定。一个点的重心坐标可以解释为放置在单纯形顶点的质量，这样该点就是这些质量的质心（或质心）。这些质量可以为零或负；当且仅当该点在单纯形内时，它们都是正数。

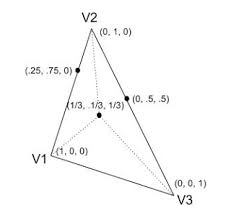
        每个点都有重心坐标，并且它的和不为零。重心坐标的两个元组当且仅当它们成比例时才指定相同的点；也就是说，如果一个元组可以通过将另一个元组的元素乘以相同的非零数来获得。因此，重心坐标要么被定义为乘以一个非零常数，要么被归一化以求和为单位。

        重心坐标在三角形几何中特别有用，可用于研究不依赖于三角形角度的性质，例如 Ceva 定理。在计算机辅助设计中，它们可用于定义某些类型的贝塞尔曲面。

8、三线性坐标系

        一个点相对于给定三角形的三线性坐标x:y:z描述了到三角形三个边线的相对定向距离。三线性坐标是齐次坐标的一个例子。比率x:y是从点到顶点A和B的对边（必要时延长）的垂直距离之比；y:z的比值是从点到分别与顶点B和C相对的边线的垂直距离的比值；同样对于z:x和顶点C和A。

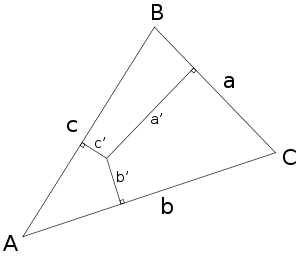
        在上图中，指示的内部点的三线性坐标是实际距离（a'，b'，c'），或者等效地以比率形式，对于任何正常数k ， ka' : kb' : kc'。如果一个点在参考三角形的边线上，则其对应的三线坐标为 0。如果外部点在三角形内部的边线的另一侧，则与该边线相关的三线坐标为负。所有三个三线性坐标都不可能是非正的。