练习推导一个最简单的BP神经网络训练过程【个人作业/数学推导】

写在前面

  各式资料中关于BP神经网络的讲解已经足够全面详尽，故不在此过多赘述。本文重点在于由一个“最简单”的神经网络练习推导其训练过程，和大家一起在练习中一起更好理解神经网络训练过程。

一、BP神经网络

1.1 简介

  BP网络（Back-Propagation Network） 是1986年被提出的，是一种按误差逆向传播算法训练的
  多层前馈网络，是目前应用最广泛的神经网络模型之一，用于函数逼近、模型识别分类、数据压缩和时间序列预测等。
  一个典型的BP网络应该包括三层:输入层、隐藏层和输出层。各层之间全连接，同层之间无连接。隐藏层可以有很多层。

Fig 1 数字图像与对应矩阵图示

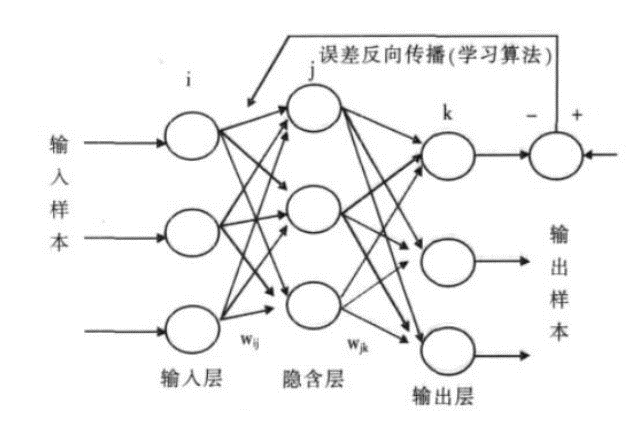
1.2 训练(学习)过程

  每一次迭代(Interation)意味着使用一批(Batch)数据对模型进行一次更新过程，被称为“一次训练”，包含一个正向过程和一个反向过程。
具体过程可以概括为如下过程：

1. 准备样本信息(数据&标签)、定义神经网络(结构、初始化参数、选取激活函数等)
2. 将样本输入，正向计算各节点函数输出
3. 计算损失函数
4. 求损失函数对各权重的偏导数，采用适当方法进行反向过程优化
5. 重复2~4直至达到停止条件

  以下训练将使用均值平方差（Mean Squared Error， MSE）作为损失函数，sigmoid函数作为激活函数、梯度下降法作为优化权重方法进行推导

二、实例推导练习作业

2.1 准备工作

Fig 2 所定义神经网络、初始化参数、样本信息等

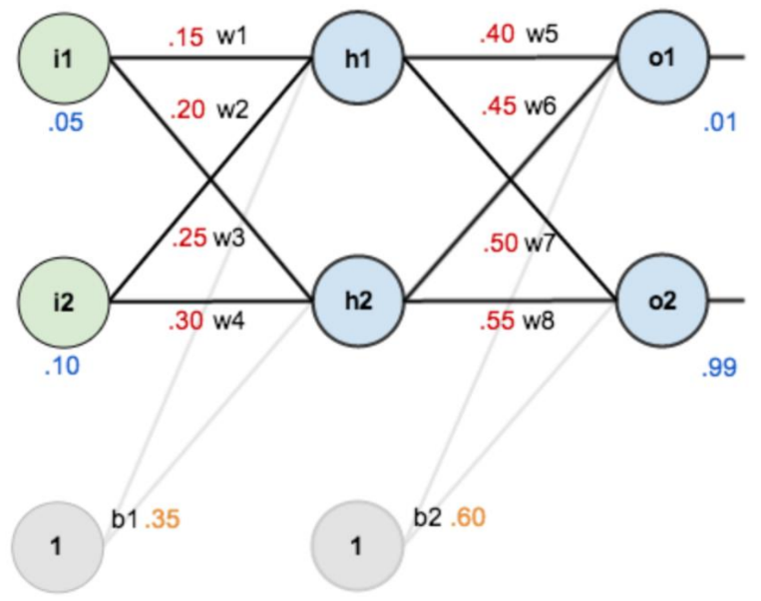
1. 第一层是输入层，包含两个神经元： i1， i2 和偏置b1
2. 第二层是隐藏层，包含两个神经元： h1， h2 和偏置项b2
3. 第三层是输出： o1， o2
4. 每条线上标的 wi 是层与层之间连接的权重
5. 激活函数是 sigmod 函数
6. 我们用 z 表示某神经元的加权输入和，用 a 表示某神经元的输出

2.2 第一次正向过程【个人推导】

  根据上述信息，我们可以得到另一种表达一次迭代的“环形”过程的图示如下：

Fig 3 bp神经网络数量关系“环”图示

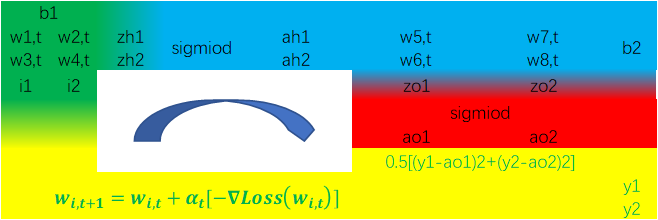
  我们做一次正向过程(由于需多次迭代，因此我们将第一次正向过程标记为t=0)，得各项数值如下：

Fig 4 初始数值“环”图示(附函数关系表达式)
  由此我们可得损失函数值为MSE=0.298371109，假设这超出了我们对损失值的要求，那么我们就需要对各个权重(wi,t=0)进行更新， 作为t=1的初始权重。

2.3 推导计算∂/∂wi【个人推导】

2.3.1 均值平方差损失函数的全微分推导

dMSE=∂MSE∂ao1dao1+∂MSE∂ao2dao2
dMSE=∂MSE∂ao1∂ao1∂zo1dzo1+∂MSE∂ao2∂ao2∂zo2dzo2
dMSE=∂MSE∂ao1∂ao1∂zo1(∂zo1∂ah1dah1+∂zo1∂ah2dah2+∂zo1∂wω5dω5+∂zo1∂wω6dω6)
dMSE=+∂MSE∂ao2∂ao2∂zo2(∂zo2∂ah1dah1+∂zo2∂ah2dah2+∂zo2∂wω7dω7+∂zo2∂wω8dω8)
dMSE=∂MSE∂ao1∂ao1∂zo1(∂zo1∂ah1∂ah1∂zh1dzh1+∂zo1∂ah2∂ah2∂zh2dzh2+∂zo1∂wω5dω5+∂zo1∂wω6dω6)
dMSE=+∂MSE∂ao2∂ao2∂zo2(∂zo2∂ah1∂ah1∂zh1dzh1+∂zo2∂ah2∂ah2∂zh2dzh2+∂zo2∂wω7dω7+∂zo2∂wω8dω8)
dMSE=∂MSE∂ao1∂ao1∂zo1[∂zo1∂ah1∂ah1∂zh1(∂zh1∂ω1dω1+∂zh1∂ω2dω2)+∂zo1∂ah2∂ah2∂zh2(∂zh2∂ω3dω3+∂zh2∂ω4dω4)+∂zo1∂wω5dω5+∂zo1∂wω6dω6]
dMSE=+∂MSE∂ao2∂ao2∂zo2[∂zo2∂ah1∂ah1∂zh1(∂zh1∂ω1dω1+∂zh1∂ω2dω2)+∂zo2∂ah2∂ah2∂zh2(∂zh2∂ω3dω3+∂zh2∂ω4dω4)+∂zo2∂wω7dω7+∂zo2∂wω8dω8]

2.3.2 这一次代入训练实例的数值和各数量名

dMSE=∂12(y1−ao1)2∂ao1dao1+∂12(y2−ao2)2∂ao2dao2
dMSE=−(y1−ao1)∂ao1∂zo1dzo1−(y2−ao2)∂ao2∂zo2dzo2
dMSE=−(y1−ao1)ao1(1−ao1)(∂zo1∂ah1dah1+∂zo1∂ah2dah2+∂zo1∂ω5dω5+∂zo1∂ω6dω6)
dMSE=−(y2−ao2)ao2(1−ao2)(∂zo2∂ah1dah1+∂zo2∂ah2dah2+∂zo2∂ω7dω7+∂zo2∂ω8dω8)
dMSE=−(y1−ao1)ao1(1−ao1)(ω5∂ah1∂zh1dzh1+ω6∂ah2∂zh2dzh2+ah1dω5+ah2dω6)
dMSE=−(y2−ao2)ao2(1−ao2)(ω7∂ah1∂zh1dzh1+ω8∂ah2∂zh2dzh2+ah1dω7+ah2dω8)
dMSE=−(y1−ao1)ao1(1−ao1)[ω5⋅ah1(1−ah1)(∂zh1∂ω1ω1+∂zh1∂ω2ω2)+ω6⋅ah2(1−ah2)(∂zh2∂ω3ω3+∂zh2∂ω4ω4)+ah1dω5+ah2dω6]
dMSE=−(y2−ao2)ao2(1−ao2)[ω7⋅ah1(1−ah1)(∂zh1∂ω1ω1+∂zh1∂ω2ω2)+ω8⋅ah2(1−ah2)(∂zh2∂ω3ω3+∂zh2∂ω4ω4)+ah1dω7+ah2dω8]
dMSE=−(y1−ao1)ao1(1−ao1)[ω5⋅ah1(1−ah1)(i1dω1+i2dω2)+ω6⋅ah2(1−ah2)(i1dω3+i2dω4)+ah1dω5+ah2dω6]
dMSE=−(y2−ao2)ao2(1−ao2)[ω7⋅ah1(1−ah1)(i1dω1+i2dω2)+ω8⋅ah2(1−ah2)(i1dω3+i2dω4)+ah1dω7+ah2dω8]

2.3.3 由此我们得到∂/∂wi的表达式

∂MSE∂ω1=−[(y1−ao1)ao1(1−ao1)⋅ω5+(y2−ao2)ao2(1−ao2)⋅ω7]⋅ah1(1−ah1)⋅i1
∂MSE∂ω2=−[(y1−ao1)ao1(1−ao1)⋅ω5+(y2−ao2)ao2(1−ao2)⋅ω7]⋅ah1(1−ah1)⋅i2
∂MSE∂ω3=−[(y1−ao1)ao1(1−ao1)⋅ω6+(y2−ao2)ao2(1−ao2)⋅ω8]⋅ah2(1−ah2)⋅i1
∂MSE∂ω4=−[(y1−ao1)ao1(1−ao1)⋅ω6+(y2−ao2)ao2(1−ao2)⋅ω8]⋅ah2(1−ah2)⋅i2
∂MSE∂ω5=−(y1−ao1)ao1(1−ao1)⋅ah1
∂MSE∂ω6=−(y1−ao1)ao1(1−ao1)⋅ah2
∂MSE∂ω7=−(y2−ao2)ao2(1−ao2)⋅ah1
∂MSE∂ω8=−(y2−ao2)ao2(1−ao2)⋅ah2

  当然如果你喜欢用矩阵表示也可以：
(P.S. Markdown编辑器承受不住如此“巨大”的矩阵算式而崩溃，我只好转成svg图片贴上了，见谅~)

【2022.06.06 update】
  对∂MSE∂ωi表达式分组并拆分矩阵：

[∂MSE∂ω1∂MSE∂ω2∂MSE∂ω3∂MSE∂ω4]=[ah1(1−ah1)ah2(1−ah2)][ω5ω6ω7ω8]T[−(y1−ao1)ao1(1−ao1)−(y2−ao2)ao2(1−ao2)][i1i2]T

[∂MSE∂ω5∂MSE∂ω6∂MSE∂ω7∂MSE∂ω8]=[−(y1−ao1)ao1(1−ao1)−(y2−ao2)ao2(1−ao2)][ah1ah2]T

  相较于之前的矩阵化分解而言，新的矩阵表示更有利于编程的代码实现。

2.4 根据∂/∂wi梯度下降法优化wi【个人推导】

  根据梯度下降法ωi,t+1=ωi,t+αt[−▽Loss(ωi,t)]，设置学习率α=0.5，计算出wi,t+1，然后重新进行下一次正向过程。(可以将该过程在Excel中轻易实现，下表中为迭代数据截取)
  可以看到，经过10001次迭代之后MSE(t=10001)=3.51019E-05已经足够小，可以停止迭代完成1代训练。

………………………………………………………………………………………………………………………………………………

sigmoid函数求导Tips(for于初级选手)

∵11+e−x=11+1ex=exex+1=1−11+ex
∴d(11+e−x)=d(1−1ex+1)
∴d(11+e−x)=(−1)×(−1)(ex+1)−2d(ex+1)
∴d(11+e−x)=ex(ex+1)2dx=−[1ex+1−1(ex+1)2]dx
∴d(11+e−x)=11+ex[1−1ex+1]dx
∴d(11+e−x)=(1−11+e−x)[11+e−x]dx