FSAF深入地分析FPN层在训练时的选择问题,以超简单的anchor-free分支形式嵌入原网络,几乎对速度没有影响,可更准确的选择最优的FPN层,带来不错的精度提升
来源:晓飞的算法工程笔记 公众号
论文: Feature Selective Anchor-Free Module for Single-Shot Object Detection

Introduction
目标检测的首要问题就是尺寸变化,许多算法使用FPN以及anchor box来解决此问题。在正样本判断上面,一般先根据目标的尺寸决定预测用的FPN层,越大的目标则使用更高的FPN层,然后根据目标与anchor box的IoU进一步判断,但这样的设计会带来两个限制:拍脑袋式的特征选择以及基于IoU的anchor采样。
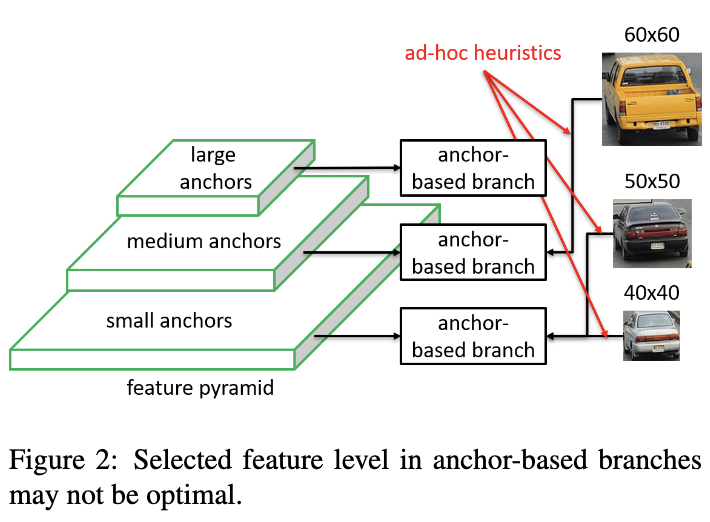
如图2所示,60x60选择中间的anchor,而50x50以及40x40的则选择最小的anchor,anchor的选择都是人们根据经验制定的规则,这在某些场景下可能不是最优的选择。

为了解决上述的问题,论文提出了简单且高效的特征选择方法FSAF(feature selective anchor-free),能够在每轮训练中选择最优的层进行优化。如图3所示,FSAF为FPN每层添加anchor-free分支,包含分类与回归,在训练时,根据anchor-free分支的预测结果选择最合适的FPN层用于训练,最终的网络输出可同时综合FSAF的anchor-free分支结果以及原网络的预测结果。
Network Architecture

FSAF的网络结果非常简单,如图4所示。在原有的网络结构上,FSAF为FPN每层引入两个额外的卷积层,分别用于预测anchor-free的分类以及回归结果。这样,在共用特征的情况下,anchor-free和anchor-based的方法可进行联合预测。
Ground-truth and Loss
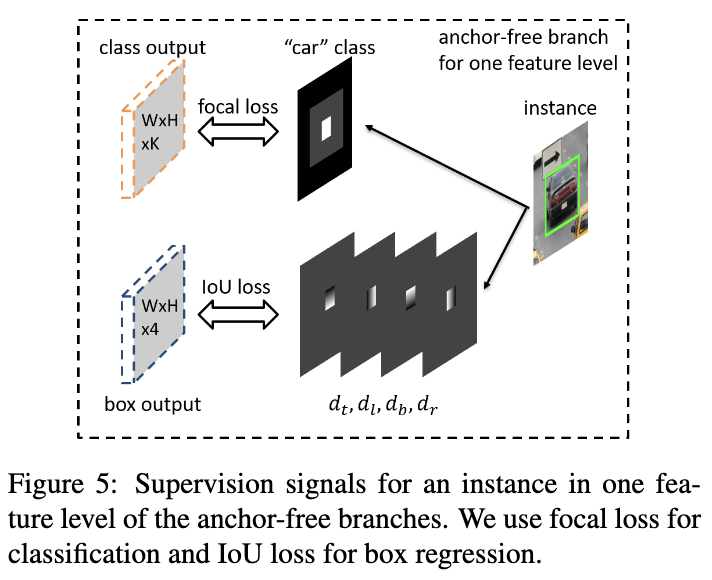
对于目标b=[x,y,w,h],在训练时可映射到任意的FPN层Pl,映射区域为blp=[xlp,ylp,wlp,hlp]。一般而言,blp=b/2l。定义有效边界ble=[xle,yle,wle,hle]和忽略边界bli=[xli,yli,wli,hli],可用于定义特征图中的正样本区域、忽略区域以及负样本区域。有效边界和忽略边界均与映射结果成等比关系,比例分别为ϵe=0.2和ϵi=0.5,最终的分类损失为所有正负样本的损失值之和除以正样本点数。
Classification Output
分类结果包含K维,目标主要设定对应维度,样本定义分以下3种情况:
- 有效边界内的区域为正样本点。
- 忽略边界到有效边界的区域不参与训练。
- 忽略边界映射到相邻的特征金字塔层中,映射的边界内的区域不参与训练
- 其余区域为负样本点。
分类的训练采用focal loss,α=0.25,γ=2.0,完整的分类损失取所有正负区域的损失值之和除以有效区域点数。
Box Regression Output
回归结果输出为分类无关的4个偏移值维度,仅回归有效区域内的点。对于有效区域位置(i,j),将映射目标表示为dli,j=[dlti,j,dlli,j,dlbi,j,dlri,j],分别为当前位置到blp的边界的距离,对应的该位置上的4维向量为dli,j/S,S=4.0为归一化常量。回归的训练采用IoU损失,完整的anchor-free分支的损失取所有有效区域的损失值的均值。
Online Feature Selection
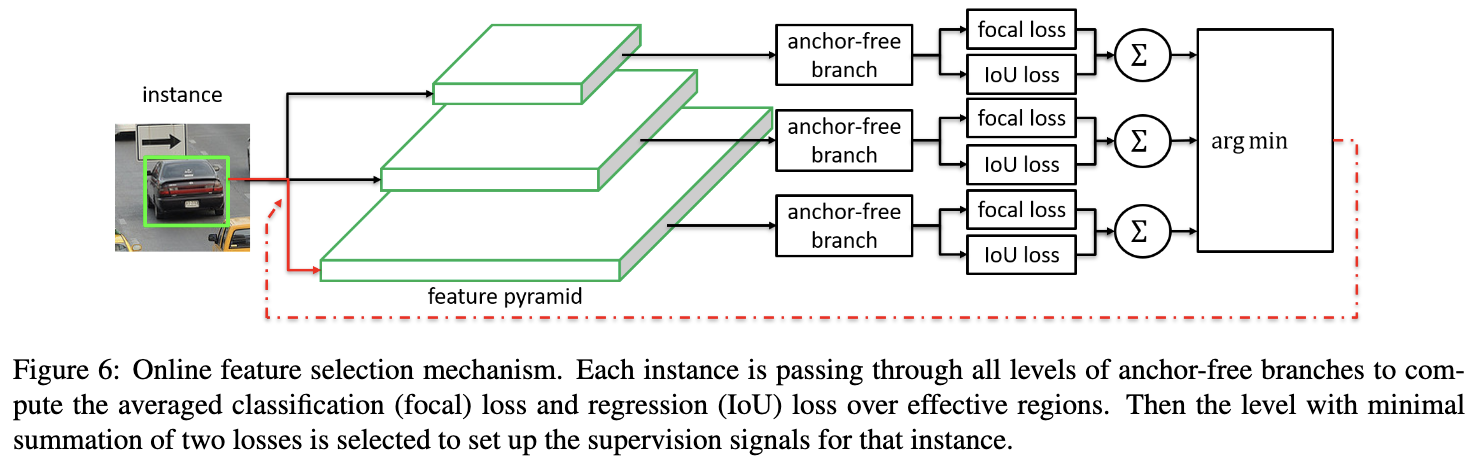
anchor-free的设计允许我们使用任意的FPN层Pl进行训练,为了找到最优的FPN层,FSAF模块需要计算FPN每层对目标的预测效果。对于分类与回归,分别计算各层有效区域的focal loss损失以及IoU loss损失:
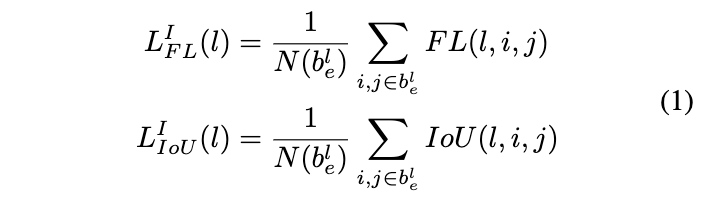
在得到各层的结果后,取损失值最小的层作为当轮训练的FPN层:
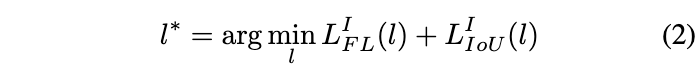
Joint Inference and Training
Inference
由于FSAF对原网络的改动很少,在推理时,稍微过滤下anchor-free和anchor-based分支的结果,然后合并进行NMS。
Optimization
完整的损失函数综合anchor-based分支以及anchor-free分支,L=Lab+λ(Lafcls+Lafreg)
Experiments
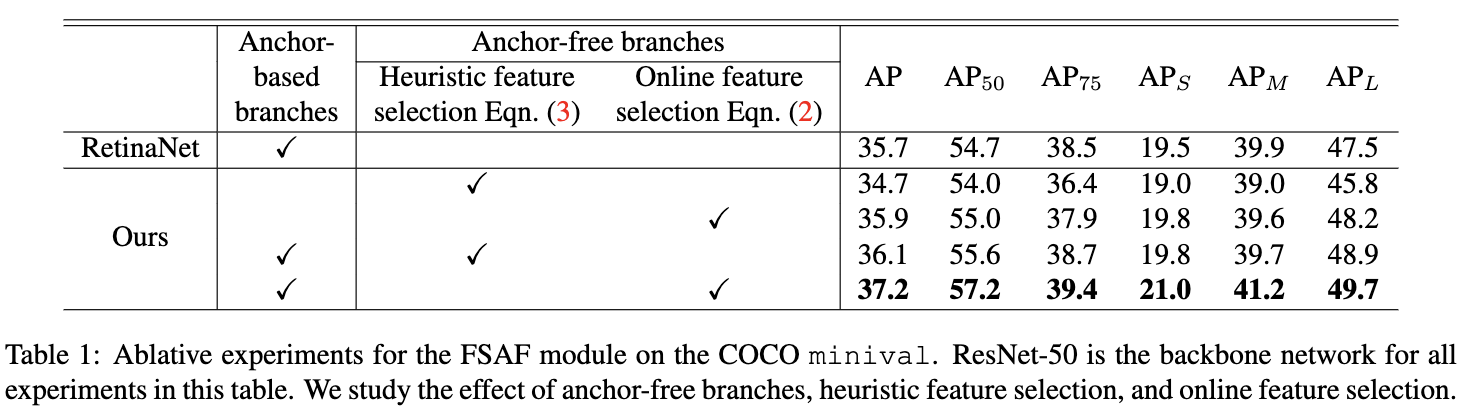
各种结构以及FPN层选择方法的对比实验。
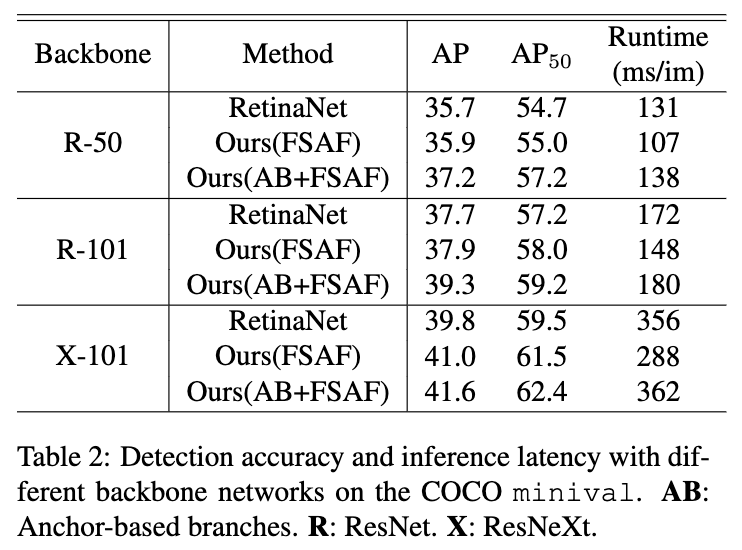
精度与推理速度对比。

与SOTA方法对比。
Conclusion
FSAF深入地分析FPN层在训练时的选择问题,以超简单的anchor-free分支形式嵌入原网络,几乎对速度没有影响,可更准确的选择最优的FPN层,带来不错的精度提升。需要注意的是,虽然抛弃以往硬性的选择方法,但实际上依然存在一些人为的设定,比如有效区域的定义,所以该方法还不是最完美的。
如果本文对你有帮助,麻烦点个赞或在看呗~
更多内容请关注 微信公众号【晓飞的算法工程笔记】
