流网络：是一个有向图（可以有环），有两个特殊的点：一个是源点（出发点），一个是汇点，每条边都有属性，叫做容量（也就是每条边的权），
可以想象成一条河，每个点就是一个汇集处，边的容量就是一段的流量。
对于反向边，可以在中间加一个点，所以我们可以默认成不存在反向边
如果边不存在，那容量就是0；
可行流（f），从源点流出，如果满足2个条件就是可行流：1容量限制 2流量守恒（对于每个点，流进多少，就流出多少）
可行流流量值（|f|）=往外流的流量 - 流回来的流量（这里考虑了反向边，但基本上是不需要考虑的）
最大流：即最大的可行流
残留网络：针对流网络的某一条可行流而言，每个可行流都对应唯一的残留网络（Gf）
残留网络的点集就是原网络的点集，边集包括原网络的所有边，和所有反向边，
残留边的容量有两种情况
对于非反向边，也就是图里的边，就是他还没有用掉的容量值，啥意思？？不是说每条边都有一个最大流量吗，那残留网络的边值就是最大流量减去原流量。
对于反向边，就是这条边能退回去多少流量，那也就是这条边的原流量
那为啥要定义这个反向边呢？？对于任意一个点你可以选择走或者是不走，但是你走着走着就发现这条路不是最优解，那你就后悔了于是要返回，返回的流量就是原来流出的流量！！
原网络的可行流（f）和残留网络可行流（f’）有啥关系？
f+f’也是原网络的一个可行流。
证明：那就看是否满足容量限制和流量守恒
分类讨论：如果这两条边的方向是相同的，我们知道残留的最大值就是c（最大容量）-f，也就是说： 0<=f'<=c-f，而原网络的的范围是 0<=f<=c，所以相加的范围就是:0<f+f'<=c，那他们就不会超限制，所以满足容量限制
如果方向不同，那又退回来一些，所以肯定不会超过限制：即：c(u,v)>=f(u,v)+f'(v,u)>=0
第二点就是流量守恒：
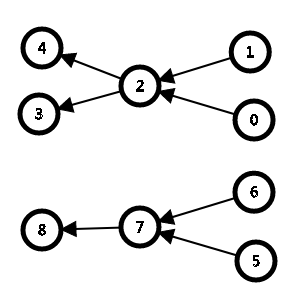
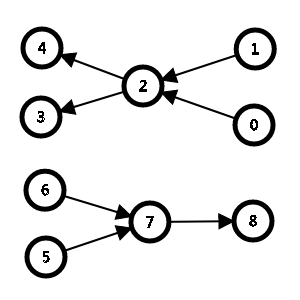
那我们可以看出来，反正两边总和是相同的，那就算是相减（反向）还是相加（正向），等号依旧是成立的
就好比 a=b , c=d => a+c=b+d , a-c=b-d
那这个可行流的流量怎么算？
| f + f' | = | f | + | f' |
得到性质：任何一个残留网络的大于零可行流都可以增加原网络里的可行流
换句话说，如果一个残留网络里没有了大于零的可行流，那原网络的可行流就一定是最大的
增广路径：
在残留网络里，从源点出发，沿着容量大于零的边，如果能走到终点的话，这条路径就是一条增广路径（一般不考虑环）
那由定义得，增广路径一定是一条可行流，有何用处？
割：
将点构成的集合V分成两部分：S和T，要求：S∪T=V，S∩T=∅，而且源点s∈S，汇点 t∈T。
那这个划分的结果就是一个割
1、割的容量：所有从S集合指向T集合的边的容量值和(顺序不能换），即c(S,T)=
最小割：割的最小容量
2.割的流量：从S指向T的流量-从T指向S的流量,即：
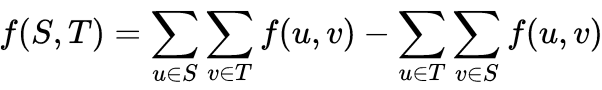
那就有以下性质：对于任意一个割，割的流量一定小于等于割的容量，即
证明：其实就是考虑不能超过最大流呗
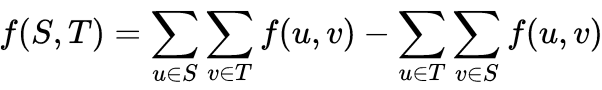
还有，就是我们刚才不是得出了：可行流流量值（|f|）=往外流的流量 - 流回来的流量，那也就是：
那我们再进阶一下：
这个就很好理解了对吧，感性理解一下吧
那现在有个大问题：就是|f|与f（S,T）之间的关系：
来证明一下吧！
∵S∪T=V,S∩T=ϕ
∴f(S,V)=f(S,S)+f(S,T)=0+f(S,T)
∴f(S,T)=f(S,V)=f(s,V)+f(S−s,V)
∵t∉S,s∉S−s
∴t,s∉S−s
设S′=S−s
∴S′是一个不包括汇点源点的集合，他一定满足流量守恒
∴f(S′,V)=∑u∈S′∑v∈Vf(u,v)−∑u∈S′∑v∈Vf(v,u)
=∑u∈S′(∑v∈Vf(u,v)−∑v∈Vf(v,u)
=∑u∈S′(0)
=0
∴f(S,T)=f(s,T)
由定义得：f(s,V)=|f|
∴f(S,T)=|f|
其实要是是在理解不了（比如我），那就感性理解一下吧！
当然，还有另一种非常简单的解法(LaTeX在博客园上太太太丑了，所以还是换回来了那个字体）：
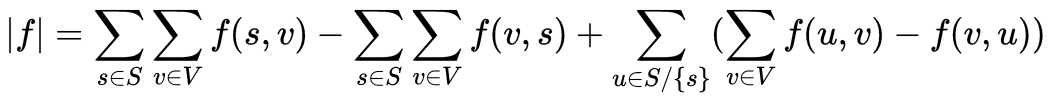
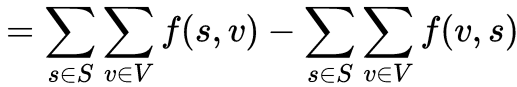
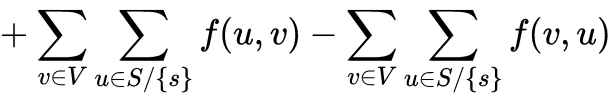
然后找到有相同的项的并合并，一约就发现有等于0的部分，然后就OK啦！！！但是由于本蒟蒻精力有限，剩下的证明就不再赘述，请谅解（其实是因为打这玩意真真真太麻烦了）
所以我们得出：
即：最大流<=最小割
下面开始进入核心部分：
关于最大流最小割定定理：
最大流=最小割
首先我们需要知道的是，对于某一个流网络来说：1可行流f是最大流 <=> 2可行流f的残留网络中不包括增广路 <=> 3存在某一个割，使得可行流的流量=割的容量
如何证明？
首先，如果 f 是最大流，而且残留网络中还有增广路，那么 f 肯定还能加，那 f 就不是最大流了，与前面假设矛盾，所以 1=>2，也就是说如果f是最大流，那f的残留网络一定不包括增广路。
其次，如果有一条可行流，他的流量等于割的容量，假设他不是最大流，那就会存在一条比他大的最大流，那这条最大流的流量一定大于割的容量，由于容量限制，这种情况是肯定不会发生的，所以如果存在一个割，他的容量等于一条可行流的流量，那么这条可行流一定是最大流，所以3=>1，搞定！
最后，将S集合定义为在残留网络中，从s（源点）出发，沿着容量大于0的可行流走，所有能走到的点，T=V - S，这就是一个合法的割，那么
，设f(x,y)<c(x,y)，那么c(x,y)-f(x,y)，也就是残留网络中的容量f'(x,y)就大于零，那也就说y这个点能从x这个点遍历到的，那么y就应该属于S，与原假设矛盾，所以f(x,y)=c(x,y)，那么对于任意的反向边一定等于0。此时我们得出，
我们还可以更深一层的发现：
由于可行流一定小于等于割的容量，对于任意的割和流这都是满足的（前提是这个割是可行的），所以我们可以得出：最大流小于等于最小割
又因为最小割<=某一个割的容量c(S,T)=|f|<=最大流，所以最大流大于等于最小割
所以最大流等于最小割
算法：给定流网络，维护残留网络
每次迭代，现在残留网络里找增广路（也就是找一条从头到尾的路径），也就是BFS。之后更新残留网络，就是让原来的残留网络Gf变成Gf+f'。咋更新？举个例子吧！
假设我现在有一条正向边和一条反向边，设正向边容量为c1，反向边的流量是c2，假设我现在流进了k个单位的流量，那么正向可以流的流量就更新成c1-k，让反向变成c2+k。
就讲到这吧！！！
拜拜！！！