论文信息
论文标题:Debiased Contrastive Learning
论文作者:Ching-Yao Chuang, Joshua Robinson, Lin Yen-Chen, Antonio Torralba, Stefanie Jegelka
论文来源:2020, NeurIPS
论文地址:download
论文代码:download
1 Introduction
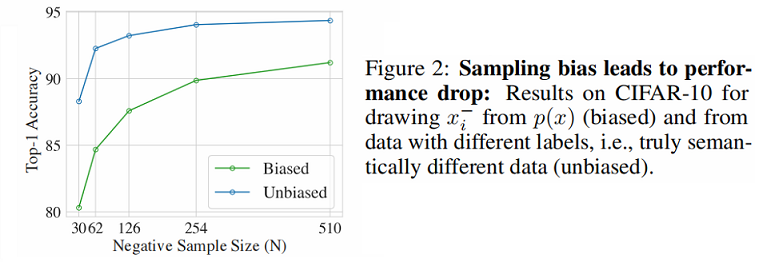
观察的结果:将拥有不同标签的样本作为负样本能显著提高性能。
对比学习思想:鼓励相似对 (x,x+)
Ex,x+,{x−i}Ni=1[−logef(x)Tf(x+)ef(x)Tf(x+)+N∑i=1ef(x)Tf(x−i)](1)
图解如下:
抽样偏差(sampling bias):由于真正的标签或真正的语义相似性通常是不可用的,负对 x− 通常从训练数据中抽取,这意味着 x− 实际上可能和 x 相似。
Figure 2 对比了不存在抽样偏差和存在抽样偏差的性能对比:
设 X 上的数据分布 p(x),代表语义意义的标签离散潜在类 C,即相似的对 (x,x+) 具有相同的潜在类。用 ρ(c) 表示类分布,得到联合分布 px,c(x,c)=p(x∣c)ρ(c)。
设 h:X→C 是潜在类标签分配函数,然后 p+x(x′)=p(x′∣h(x′)=h(x)) 中观察到的 x′ 是 x 的正对的概率,p−x(x′)=p(x′∣h(x′)≠h(x)) 中观察到的 x′ 是 x 的负对的概率。
假设类 c 概率 ρ(c)=τ+ ,不是的概率为 τ−=1−τ+ 。
综上,对比损失函数可以优化为:
LNUnbiased (f)=Ex∼p,x+∼p+−x−i∼p−x[−logef(x)Tf(x+)ef(x)Tf(x+)+QNN∑i=1ef(x)Tf(x−i)](2)
其中,Q 代表着权重参数。当 Q=N 时,即标准的对比损失函数。
对有偏对比损失函数和无偏对比损失函数的分析:
Lemma 1. For any embedding f and finite N, we have
LNBiased (f)≥LNUnbiased (f)+Ex∼p[0∧logEx+∼p+xexpf(x)⊤f(x+)Ex−∼p−xexpf(x)⊤f(x−)]−e3/2√π2N(3)
where a∧b denotes the minimum of two real numbers a and b.
Lemma 1 所带来的问题:
-
- 无偏损失越小,第二项就越大,差距就越大;
- 最小化 LNBiased 的上界和最小化理想情况的 LNUnbiased 所产生的潜在表示是不同的;
2 Method
我们首先将数据分布(data distribution)分解为【当从 p(x) 中提取样本时,样本 x−i 将来自与 x 相同的类,概率为 τ+。】
p(x′)=τ+p+x(x′)+τ−p−x(x′)
相应的
p−x(x′)=(p(x′)−τ+p+x(x′))/τ−
Eq.2 的一种替代形式:
1(τ−)NN∑k=0(Nk)(−τ+)kExpp,x+∼p+x{x−i}ki=1∼p+x{x−i}Ni=k+1∼p[−logef(x)Tf(x+)ef(x)Tf(x+)+N∑i=1ef(x)Tf(x−i)](4)
为了得到一个更实际的形式,我们考虑了负例数 N 趋于无穷时的渐近形式。
Lemma 2. For fixed Q and N→∞ , it holds that
Ex∼p,x+∼p+x{x−i}Ni=1∼p−Nx[logef(x)Tf(x+)ef(x)Tf(x+)+QNN∑i=1ef(x)Tf(x−i)](5)
⟶˜LQDebiased =Ex+∼p+x[−logef(x)Tf(x+)ef(x)Tf(x+)+Qτ−(Ex−∼p[ef(x)Tf(x−)]−τ+Ev∼p+x[ef(x)Tf(v)])](6)
Eq.6 仍然从 p 中取样例子 x− ,但用额外的正样本 v 来修正。这本质上是重新加权分母中的正项和负项。
经验估计 ˜LQDebiased 比直接的 Eq.5 更容易计算。在数据分布 p 中采样 N 个样本 {ui}Ni=1,在分布 p+x 中采样 M 个样本 {ui}Mi=1,将 Eq.6 分母中的第二项重新估计为:
g(x,{ui}Ni=1,{vi}Mi=1)=max{1τ−(1NN∑i=1ef(x)Tf(ui)−τ+1MM∑i=1ef(x)Tf(vi)),e−1/t}(7)
我们约束估计量 g 大于它的理论最小值 e−1/t≤Ex−∼p−xef(x)Tf(x−i) 以防止计算一个负数的对数。当数据N 和 M 固定后,由此产生的损失为
LN,MDebiased (f)=Ex∼p;x+∼p+x{ui}Ni=1∼pN{vi}Ni=1∼p+Mx[−logef(x)Tf(x+)ef(x)Tf(x+)+Ng(x,{ui}Ni=1,{vi}Mi=1)](8)
其中,为简单起见,我们将 Q 设置为有限的 N。类先验 τ+ 可以从数据中估计或作为一个超参数处理。Theorem 3 将有限 N 和 M 引起的误差限定为随速率 O(N−1/2+M−1/2) 递减。
Theorem 3. For any embedding f and finite N and M , we have
|˜LNDebiased (f)−LN,MDebiased (f)|≤e3/2τ−√π2N+e3/2τ+τ−√π2M(9)
实验表明,较大的 N 和 M 始终会导致更好的性能。在实现中,我们对 LN,MDebiased 使用一个完整的经验估计,以平均在 T 个点 x 上,有限 N 和 M 的损失。
3 Experiments
实验结果
- 新的损失在视觉、语言和强化学习基准上优于先进的对比学习;
- 学习到的嵌入更接近理想的无偏目标;
- 大 N 大 M 提高性能;甚至一个比标准 M=1 更积极的例子可以明显帮助;
__EOF__