算法效率的计算

一、如何衡量一个算法的好坏？

如果一个算法运行速度快且消耗内存少，那么该算法一定是一个效率高的好算法。那么如何计算一个算法的速度和消耗的内存呢？通常我们使用时间复杂度和空间复杂度来衡量一个算法的好坏，并且使用大O表示法来表示。

二、时间复杂度

1. 时间复杂度的计算方法

一、确定基本操作
首先，明确算法中的基本操作。基本操作通常是指算法中执行次数最多或者对时间影响最大的操作。例如，在一个循环中，循环体的执行次数通常是基本操作；在排序算法中，比较操作和交换操作可能是基本操作。

二、分析基本操作的执行次数与问题规模的关系

1. 用问题规模的变量来表示基本操作的执行次数。例如，如果算法是对一个长度为 n 的数组进行操作，那么问题规模通常用 n 表示。
2. 分析算法的结构，确定基本操作的执行次数与问题规模之间的关系。这可能需要对算法进行逐步分析，考虑不同的情况和分支。

三、用大 O 记号表示时间复杂度

1. 忽略低阶项和系数。在表示时间复杂度时，只关注最高阶项，因为当问题规模足够大时，低阶项和系数对时间的影响相对较小。
2. 根据基本操作的执行次数与问题规模的关系，常见的时间复杂度级别有常数阶 O (1)、对数阶 O (log n)、线性阶 O (n)、线性对数阶 O (n log n)、平方阶 O (n²) 等。

用作者的话来说，就是有循环就计算整个算法中循环语句的执行次数，没有循环就计算整个算法所执行的所有语句数。然后用问题的规模的变量把这个计算结果表示出来，最后使用大O表示法去掉最高项的系数，只保留最高项的阶数，结果就是该算法的时间复杂的大O表示法。如果该算法中有函数调用或者递归也是同样的计算方法。

2. 时间复杂度习题

例题1

void Func1(int N)
{
	int count = 0;
	for (int i = 0; i < N ; ++ i)
	{
		 for (int j = 0; j < N ; ++ j)
		 {
			 ++count;
		 }
	}
 
	for (int k = 0; k < 2 * N ; ++ k)
	{
		 ++count;
	}
	 
	int M = 10;
	while (M--)
	{
		 ++count;
	}
｝

首先，有循环就计算循环语句的执行次数，n² + 2n + 10
其次，从该函数的参数判断该算法的规模为 n
接着，使用规模变量表示前面的执行次数，n² + 2n + 10
最后，使用大O表示法，去掉最高阶系数，只保留最高阶，O(n²)

例题2
下面是一个计算前 n 项正整数之和的算法：

// 计算前 n 项和
long long sum_first_n(int n)
{
	int i;
	long long sum = 0;
	for (i = 1; i <= n; ++i)
		sum += i;
	// 返回
	return sum;
}

首先，有循环，那么就计算循环语句的执行次数，n。
然后，该算法是计算前 n 项正整数的和，规模变量为 n。
接着用规模变量表示前面计算的执行次数，n。
最后使用大O表示法，去掉最高阶系数，只保留最高阶，O(n)。

例题3

// 计算Func3的时间复杂度？
void Func3(int N, int M)
{
	 int count = 0;
	 for (int k = 0; k < M; ++ k)
	 {
		 ++count;
	 }
 
	 for (int k = 0; k < N ; ++ k)
	 {
		 ++count;
	 }
	 printf("%d\n", count);
}

有了上面两个练习，下面的题目就写得简洁一些了。
循环语句执行次数：M+N
规模变量表示：M+N
如果题目说明 M 远大于 N，则 O(M)，如果 N 远大于 M，则O(N)，如果没有说明则 O(M+N)。

例题4

// 计算Func4的时间复杂度？
void Func4(int N)
{
	 int count = 0;
	 for (int k = 0; k < 100; ++ k)
	 {
		 ++count;
	 }
	 printf("%d\n", count);
}

循环语句执行次数：100
问题规模变量表示：100
结果为常数，那就是常数阶O(1)，不管这个常数多大，只要是一个常数那都是O(1)

例题5

// 计算strchr的时间复杂度？
const char * strchr ( const char * str, int character );

库函数 strchr() 的功能是在一个字符串中查找指定字符，如果找到了就返回该字符的地址，如果没找到就返回空指针。

那么通过计算，该算法的时间复杂度并不唯一，如果带查找的字符刚好在第一个，那么只需要查找一次，时间复杂度也就是O(1)；如果带查找的字符刚好在最后一个，那么需要查找 n 次，时间复杂度也就是O(n)。

在这种存在最好和最坏的情况的算法中，通常是取最坏的情况。那么该算法的时间复杂度就是 O(n)。

例题6
下面是一个优化过后的冒泡排序：

// 计算BubbleSort的时间复杂度？
void BubbleSort(int* a, int n)
{
	 assert(a);
	 for (size_t end = n; end > 0; --end)
	 {
		 int exchange = 0; 
		 for (size_t i = 1; i < end; ++i)
		 {
			 if (a[i-1] > a[i])
			 {
				 Swap(&a[i-1], &a[i]);
				 exchange = 1;
			 }
		 }
	 	 // 判断本次比较中是否交换
		 if (exchange == 0)
		 break;
	 }
}

该冒泡排序算法也存在最好和最坏两种情况：
（1）当待排序数组完全有序，那么第一轮比较之后就会跳出循环。那么循环中 if 条件语句执行的次数为 n-1，其时间复杂度也就是 O(n)
（2）当待排序数组完全逆序，那么冒泡排序就会一直执行到结束。那么循环中 if 条件语句的执行次数为 (n-1)+(n-2)+…+1，其时间复杂度为 O(n²)

例题7
下面是一个二分查找的算法：

// 计算BinarySearch的时间复杂度？
int BinarySearch(int* a, int n, int x)
{
 	 assert(a);
 
	 int begin = 0;
	 int end = n-1;
	 while (begin < end)
	 {
	 	 // 取得中间数
		 int mid = begin + ((end-begin)>>1);
		 // 判断
		 if (a[mid] < x)
		 	begin = mid+1;
		 else if (a[mid] > x)
		 	end = mid;
		 else
		 	return mid;
	 }
	 
	 return -1;
}

二分查找是在 n 个有序的数中查找一个数，而且每次查找都可以去掉一半的数，也就是剩下 n/2 个数。最坏的情况就是查找到最后一个数，也就是 n/2/2/2…/2 = 1，即 2^k = n，k = log₂n，这个 k 也就是要查找的次数，且每次查找所执行的语句也是常数，所以该算法的时间复杂度就是 O(log₂n)，也就是上面说的对数阶。

例题8
下面是计算正整数 n 的阶乘的递归算法：

// 计算阶乘递归Fac的时间复杂度？
long long Fac(size_t N)
{
 if(0 == N)
 return 1;
 
 return Fac(N-1)*N;
}

通过计算，该函数加上递归一共需要被调用 N+1 次，每次调用该函数执行常数条语句，所以该算法的时间复杂度为 O(n)

例题9
下面是第 n 项斐波那契数列的递归算法：

// 计算斐波那契递归Fib的时间复杂度？
long long Fib(size_t N)
{
	 if(N < 3)
	 	return 1;
	 
	 return Fib(N-1) + Fib(N-2);
}

首先，递归调用一次执行常数条语句，那么一共递归调用多少次？

如上图所示，我们把缺失的项设置为 k，那么递归调用的次数为：2⁰ + 2¹ + 2² +…+ 2^n-1 - k = 2ⁿ - 1 - k，相比于 2ⁿ 来说 1+k 显得微不足道，所以该求斐波那契第 n 项的递归算法的时间复杂度为 O(2ⁿ)

三、空间复杂度

1. 空间复杂度的计算方法

有了前面时间复杂度的计算方法，那么空间复杂度的计算就要简单很多了。
（1）统计创建变量的个数（不管是什么类型）
（2）用问题的规模变量表示变量的总个数
（3）大O表示法，去掉最高阶的系数，只保留最高阶

2. 空间复杂度习题

习题1
下面是优化过后的冒泡循环：

// 计算BubbleSort的空间复杂度？
void BubbleSort(int* a, int n)
{
	 assert(a);
	 for (size_t end = n; end > 0; --end)
	 {
		 int exchange = 0;
		 for (size_t i = 1; i < end; ++i)
		 {
			 if (a[i-1] > a[i])
			 {
				 Swap(&a[i-1], &a[i]);
				 exchange = 1;
			 }
		 }
		 // 判断本躺排序是否交换
		 if (exchange == 0)
		 	break;
	 }
}

由于在执行算法的过程中只开辟了常数个变量（end、i 和 exchange），所以该算法的空间复杂度为 O(1)

习题2
下面是阶乘的递归算法：

// 计算阶乘递归Fac的空间复杂度？
long long Fac(size_t N)
{
	 if(N == 0)
	 	return 1;
	 
	 return Fac(N-1)*N;
}

虽然在递归的过程中没有开辟新的变量，但是每次递归都需要开辟栈帧空间，一共递归 n+1 次，开辟了 n+1 个栈帧空间，所以该算法的空间复杂度为 O(n)

习题3
下面是第 n 项斐波那契数列的递归算法：

// 计算斐波那契递归Fib的时间复杂度？
long long Fib(size_t N)
{
	 if(N < 3)
	 	return 1;
	 
	 return Fib(N-1) + Fib(N-2);
}

前面通过画图的方式的出，该递归需要调用 2ⁿ 层级的次数，那么是否需要开辟 2ⁿ 层级的函数栈桢？

答案肯定不是，仔细阅读代码，你会发现，每次递归调用函数 Fib 时，它都会先调用左边的 Fib(N-1)，然后再在里面调用他自己的 Fib(N-1)，直到最后一次递归时它的 N-1 < 3 时才会返回上一层递归，然后调用该层递归的 Fib(N-2)。如下图：

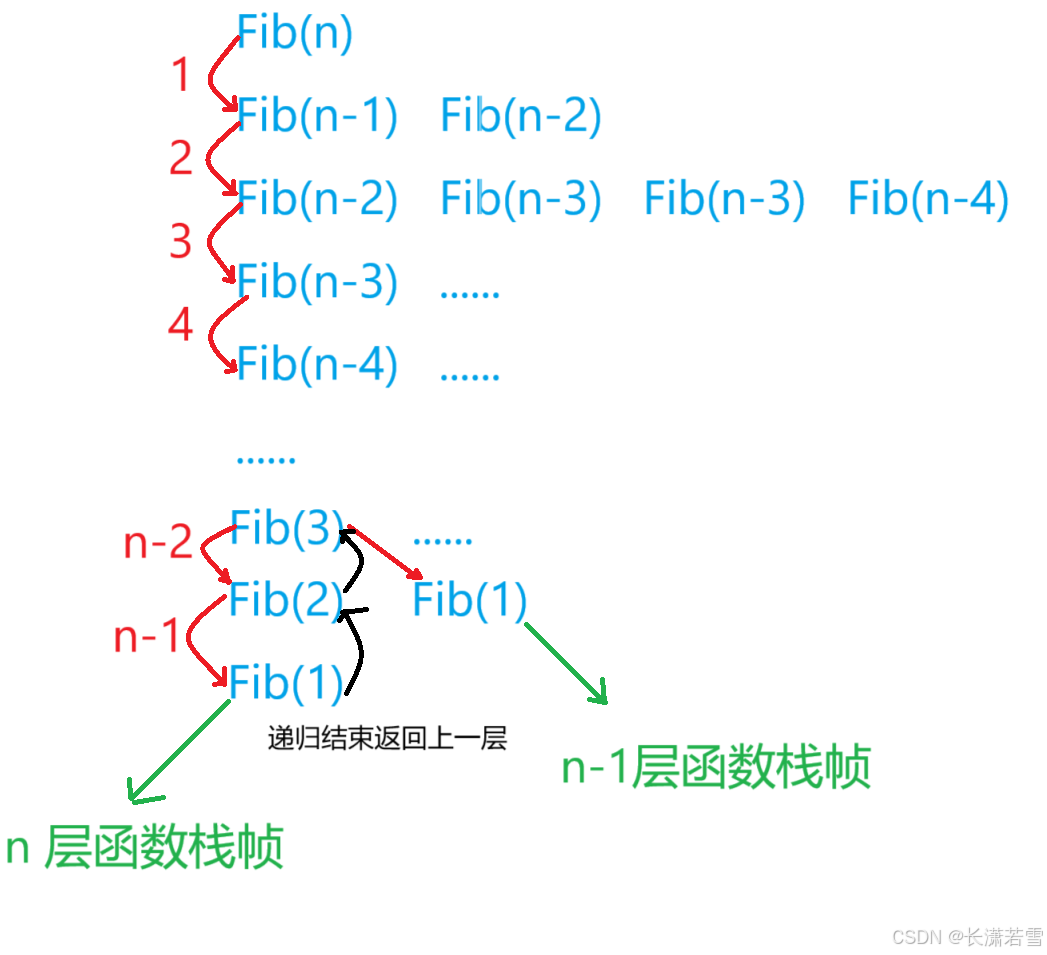
所以，该算法运行时函数栈帧消耗的最大层数为 n，所以该算法的空间复杂度为 O(n)

四、常见复杂度对比

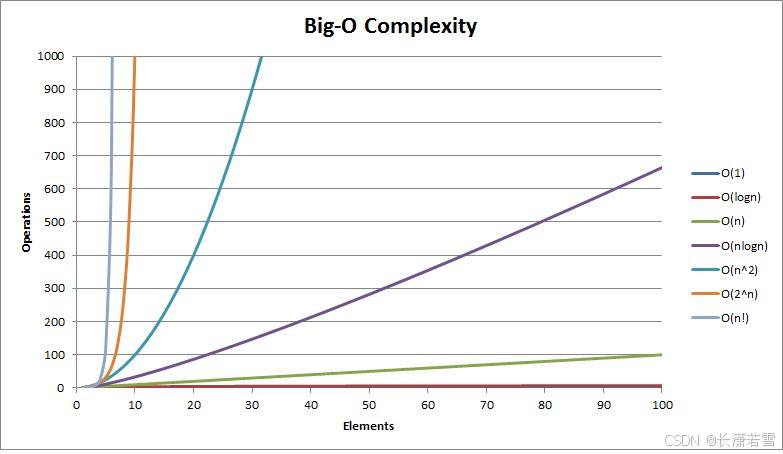
上述图片均来自比特的课件哈，作者比较懒也不会画。

五、复杂度oj题

1. 消失的数字

题目描述： 数组nums包含从 0 到 n 的所有整数，但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在 O(n) 的时间复杂度内完成吗？

注意：本题相对书上原题稍作改动

示例 1：
输入：[3,0,1]
输出：2

示例 2：
输入：[9,6,4,2,3,5,7,0,1]
输出：8

题目OJ链接： 链接: link

题目解析：
（1）题目要求时间复杂度需要 <= O(n)
（2）三种算法：

a. 计算 0 - n 的和然后减去数组的每个元素，结果就是缺失的数

// 计算 0 - n 的和，然后减去数组的每个元素
int find_missing_num(int *arr, int sz)
{
	// 计算 0-n 之和
	int sum = (sz + 1) * sz / 2;
	// 减去数组的每个元素
	int i;
	for (i = 0; i < sz; ++i)
	{
		sum -= arr[i];
	}
	// 返回
	return sum;
}

时间复杂度： O(n)
空间复杂度： O(1)

b. 用 0 - n 与数组的每个元素异或，结果就是缺失的数

int find_missing_num(int* arr, int sz)
{
	int result = sz;
	int i;
	for (i = 0; i < sz; ++i)
	{
		result ^= i ^ arr[i];
	}
	// 返回
	return result;
}

由于循环是 0 - n-1，所以 result 的初值为 sz。

时间复杂度： O(n)
空间复杂度： O(1)

c. 使用 calloc() 函数动态开辟一个大小为 n+1 的 int 数组，该数组用来统计 0 - n 的出现次数，遍历原数组，记录出现次数，然后遍历次数数组，出现次数为 0 的就是缺失的数。

int find_missing_num(int* arr, int sz)
{
	// 动态开辟次数数组
	int* times = (int*)calloc((sz + 1), sizeof(int));
	// 遍历原数组统计次数
	int i;
	for (i = 0; i < sz; ++i)
		++times[arr[i]];
	// 遍历次数数组找缺失数
	for (i = 0; i <= sz; ++i)
	{
		if (0 == times[i])
			break;
	}
	// 释放
	free(times);
	times = NULL;
	// 返回
	return i;
}

时间复杂度： O(n)
空间复杂度： O(n)

2. 轮转数组

题目描述： 给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]

示例 2:
输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]

提示：
1 <= nums.length <= 105
-231 <= nums[i] <= 231 - 1
0 <= k <= 105

题目OJ链接： 链接: link

题目解析：
（1）像这种旋转数组或者字符串的问题，不管是右旋转还是坐旋转，当旋转次数为其长度的整数倍时，就会复原。也就是旋转的周期是其长度，如：1,2,3,4，右旋转或者左旋转 4n 次后复原。所以，实际的旋转次数需要对其长度取余。

（2）三种解法：

a. 暴力求解法
就是直接一步一步旋转，没有任何技巧可言

// 暴力求解法
void rotate_arr_i(int* arr, int sz, int k)
{
	// 实际旋转次数
	int n = k % sz;
	// 旋转
	while (n--)
	{
		// 存储尾元素
		int tmp = arr[sz - 1];
		// 前面元素往后移
		int i;
		for (i = sz - 1; i > 0; ++i)
			arr[i] = arr[i - 1];
		// 尾元素放开头
		arr[0] = tmp;
	}
}

时间复杂度： O(n²)
空间复杂度： O(1)

b. 三步逆序法（三种里面最优）
先计算实际旋转次数 k，然后把后 k 项逆序，再把前 sz-k 项逆序，最后整个数组逆序，就是想要的结果。

// 三步逆序法

// 逆序
void reverse(int* left, int* right)
{
	while (left < right)
	{
		// 交换
		int tmp = *left;
		*left = *right;
		*right = tmp;
		// 下一组
		++left;
		--right;
	}
}

// 三步
void rotate_arr_i(int* arr, int sz, int k)
{
	// 实际旋转次数
	k %= sz;
	// 三步逆序
	reverse(arr + sz - k, arr + sz - 1);
	reverse(arr, arr + sz - k - 1);
	reverse(arr, arr + sz - 1);
}

时间复杂度： O(n)
空间复杂度： O(1)

c. 额外开辟数组法
这是一个空间换时间的方法，额外开辟一个大小相同的动态数组，然后算出实际旋转次数 k，把后 k 项放在新数组前面，再把前 sz-k 项放在新数组后面，最后把新数组拷贝到原数组。

// 额外开辟数组法
void rotate_arr_i(int* arr, int sz, int k)
{
	// 实际旋转次数
	k %= sz;
	// 开辟额外数组
	int* tmp = (int*)malloc(sizeof(int) * sz);
	// 把原数组旋转后的顺序拷贝到新数组
	int i;
	for (i = 0; i < k; ++i)
		tmp[i] = arr[sz - k + i];

	for (i = 0; i < sz - k; ++i)
		tmp[k - 1 + i] = arr[i];
	// 把新数组拷贝到原数组
	for (i = 0; i < sz; ++i)
		arr[i] = tmp[i];

	// 释放额外数组
	free(tmp);
}

时间复杂度： O(n)
空间复杂度： O(n)