【practise】逆波兰表达式求值

1.前言

计算器是怎么识别我们输入的数字并进行计算的？如何确定给定字符串运算符运算数的优先级？本文简单介绍计算器计算识别的方法之一——后缀表达式

2.题目简介

题目链接：LINK

逆波兰表达式：又称后缀表达式，我们平时写的类似于“a+b+d”是中缀表达式，中缀表达式适合人类进行识别运算，但相对于计算机适合用后缀表达式。

题意很简单，给定一个后缀表达式，请运算得出结果并且返回。

想要完成这道题，我们首先来理解后缀表达式的运算逻辑。参考：LINK

3.求解思路

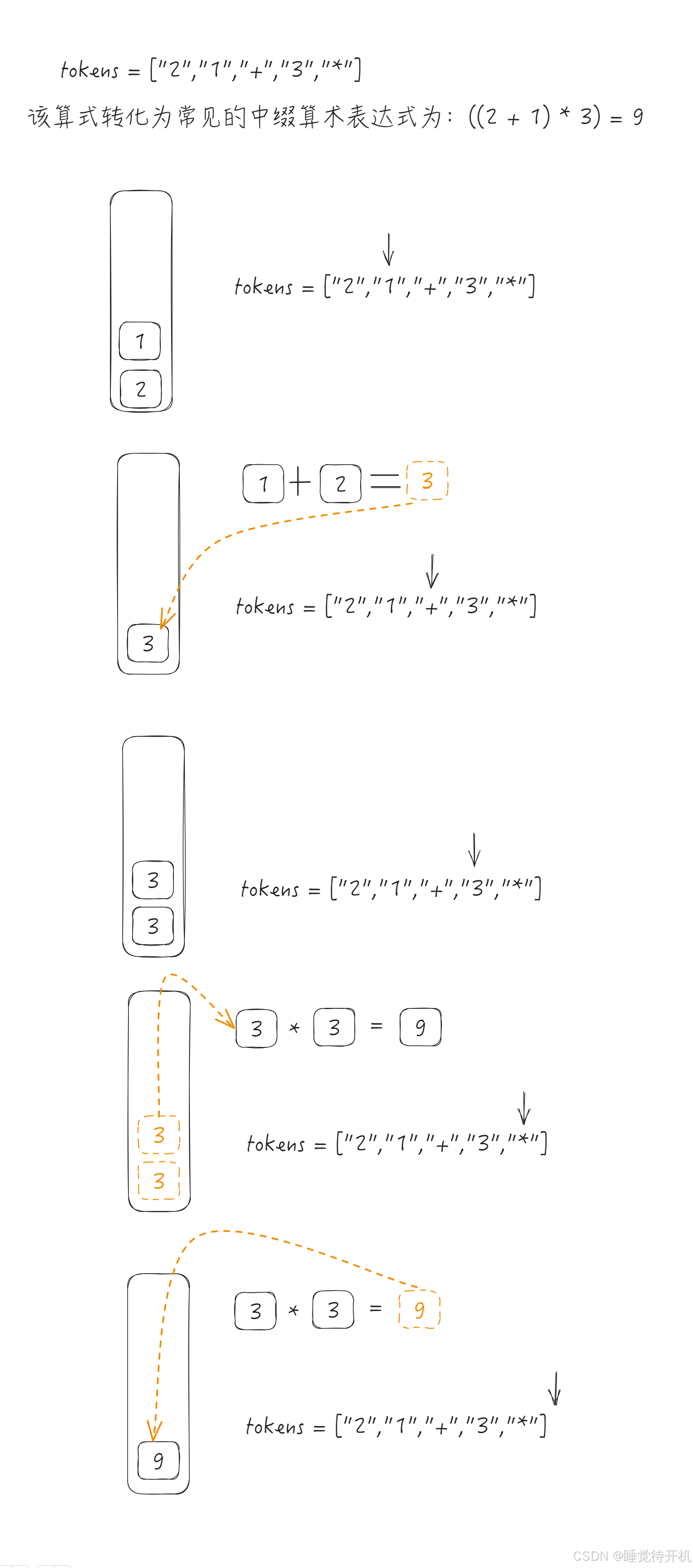
题解思路很简单，用栈模拟出计算过程即可。

运算逻辑是：遍历tokens字符串，

• 运算符，取两个操作数进行运算。
• 运算数，入栈，等待运算。

4.示例代码

class Solution {
public:
    int evalRPN(vector<string>& tokens) {
        stack<int> st; //用于运算的栈
        set<string> s = { "+", "-", "*", "/" }; //用于判断是否是运算符的set

        for(auto& e: tokens)
        {
            //如果是操作符，就取数据运算
            if(s.find(e) != s.end())
            {
                int right = st.top();
                st.pop();
                int left = st.top();
                st.pop();

                switch(e[0])
                {
                    case '+':
                    st.push(left + right);
                    break;
                    case '-':
                    st.push(left - right);
                    break;
                    case '*':
                    st.push(left * right);
                    break;
                    case '/':
                    st.push(left / right);
                    break;
                }
            }
            else
            {
                //如果是操作符，那么就入栈
                st.push(stoi(e));
            }
        }

        return st.top();
    }
};

---

---

EOF