-
红黑树基本操作
记录一下红黑树的学习笔记
学习视频:
红黑树定义及插入
红黑树删除
视频讲的非常好非常详细,动画非常形象,强烈建议去看看。本文的图文来自视频1. 红黑树定义
红黑树是一种自平衡的二叉搜索树。所以红黑树首先必须是一棵二叉搜索树(左根右),其次满足以下三条性质:
- 根性质:根节点和叶子节点都是黑色(根叶黑)
- 红性质:红节点的孩子节点必须是黑色,换句话说,不存在连续的两个红色节点(不红红)
- 黑性质:任意节点到叶子节点的路径上黑色节点数量相同,注意空节点是黑色节点(黑路同)
总结起来,红黑树的口诀就是:左根右,根叶黑,不红红,黑路同。如下图:

根据定义,可以推断出红黑树的最长路径不会超过最短路径的两倍,换句话说,任一节点的左右子树高度相差不会超过两倍。
对比AVL树,任一节点的左右子树高度的绝对值相差不超过1。所以AVL树对于平衡的把控更加严格,所以在查询效率上,红黑树要比AVL树稍差,但时间复杂度都是同一个数量级(都是log n)。
也正因为AVL树对平衡的要求更高,所以在插入/删除后需要调整平衡的次数更多,因此在插入和删除的效率上, 红黑树比AVL树更高。
2. 红黑树插入
首先插入的新节点默认为红色。因为如果默认为黑色,必然导致这条路径多一个黑色节点,违反了黑路同性质。
插入新节点如果破坏了红黑树性质,分为三种情况进行调整:- 插入节点是根节点(破坏了根叶黑)
- 插入节点的叔叔的红色(破坏了不红红)
- 插入节点的叔叔是黑色(破坏了不红红)
对于第一种情况,是最简单的。如果插入的是根节点,违反了根叶黑性质,直接把他变成黑色即可。后面两种情况就要根据插入节点的叔叔颜色判断。
第二种情况,如果叔叔是红色,就需要按叔父爷变色,爷爷变插入节点进行变化,变化后再判断爷爷节点是否符合红黑树性质。注意,下图没有画出叶子节点

第三种情况要复杂些。需要先旋转再变色,旋转根据AVL中的(LL型、RR型、LR型、RL型)进行判断。
例如下图,是LL型的调整过程,RR型类似
下图是LR型的调整过程,RL型类似
插入操作容易破坏红黑树的不红红性质3. 红黑树删除
删除是红黑树最难最复杂的操作,删除容易破坏黑路同的性质。总体上也分为三种情况:
- 没有孩子----->直接删除
- 只有左子树/只有右子树----->直接代替
- 左右子树都有,转换成前两种情况
看起来好像不复杂,但需要分的情况较多。对于第二种情况,只可能出现一黑一红(红在左子树)和一黑一红(红在右子树)两种。所以实际上是只有左孩子或只有右孩子,那么直接用孩子代替即可。例如下图(没画出空节点),要删除17

对于没有孩子的情况,又需要分删除的节点是黑色还是红色。
如果删除的是红色,因为不会破坏黑路同性质,所以直接删除即可。例如下图,删除23
然后就是最复杂的一种情况,删除的是没有孩子的黑色节点。因为删除的是黑色节点,所以必然会破坏黑路同性质,因此必然要进行调整。注意,这里的孩子是不包括空节点的。(ps:接下来分的情况很多,会有点晕)
这里先引入双黑节点的概念,因为少了一个黑色节点,所以让一个节点算双重黑色,就是双黑节点。如下图
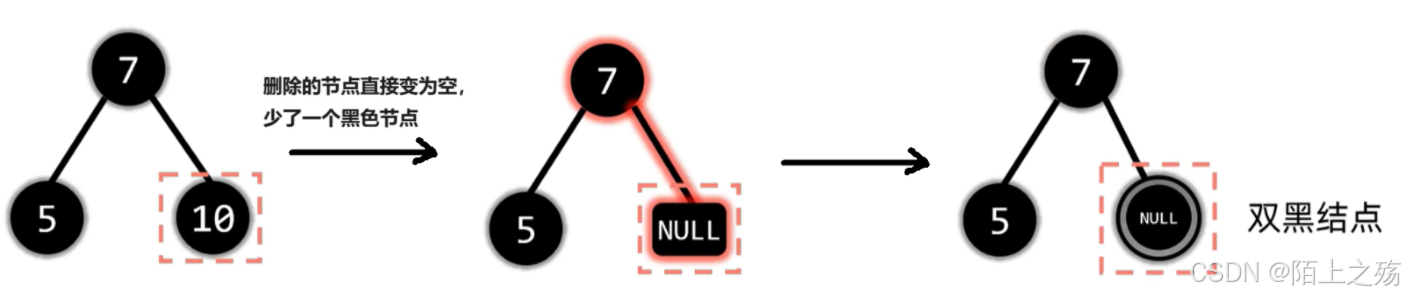
接下来的任务就是要消除双黑节点或者让他变成单黑节点
消除的方法是看双黑节点的兄弟是黑色还是红色。兄弟是黑色节点又要分兄弟至少有一个红孩子(先变色,后旋转)和兄弟的孩子都是黑色两种情况。
对于至少一个红孩子的情况,如下图(展示的是LL型),注意其中r变s,s变p,p变黑指的是r变成s的颜色,s变成p的颜色,p变成黑色,LL型和RR型类似

对于LR型,如下图,RL型类似

对于兄弟的孩子都是黑色的情况,如下图

双黑节点的兄弟是红色的情况:

最后对删除进行一下总结:

上面只是对各种情况进行一个简单的记录,更多例子和细节建议去看这个up主的视频,强推! -
相关阅读:
BeautifulSoup的使用
Placement Rules 使用文档
Redis的发布订阅在SpringMVC(或xml配置)项目中使用(注意版本兼容问题)
六级词汇讲义
【更新】囚生CYのMemo(20231118~)
MPLS 初见
mysql-发生系统错误1067
详解CAN总线:CAN总线报文格式—数据帧
NodeJs 面试题 2022.6
奥拉帕尼人血清白蛋白HSA纳米粒|陶扎色替卵清白蛋白OVA纳米粒|来他替尼小鼠血清白蛋白MSA纳米粒(试剂)
- 原文地址:https://blog.csdn.net/weixin_45186425/article/details/140441266