数据结构--二叉树遍历

目录

1.介绍

（1）前序遍历

（2）定义结构体

（3）前序遍历实现

（4）中序遍历实现

（5）二叉树的节点个数

（6）二叉树树叶节点个数

（7）二叉树的高度

（8）二叉树节点的开辟

（9）建立一个测试二叉树

（10）测试二叉树相关函数的功能

（11）第k层的数据个数

（12）二叉树里面查找节点

---

1.介绍

（1）前序遍历

前序遍历就是针对于树根而言的，就是这个树的树根是先被我们遍历的，因为这个二叉树里面划分为树根，左子树和右子树，这个前中后表示的就是这三个里面的树根的访问顺序，树根先被访问就是前序遍历，树根是第二个被访问的就是中序遍历，最后被访问到就是后序遍历；

（2）定义结构体

下面看一下这个前序遍历的具体实现；

首先我们要进行这个结构体的定义，这个结构体就是表示的每一个节点，具体来讲就是包括这个节点数据，节点的左节点，节点的右节点；

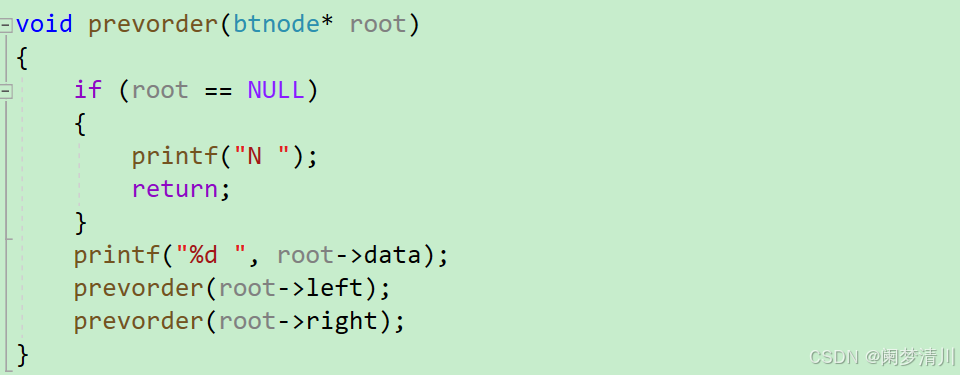
（3）前序遍历实现

这个代码里面的N表示的就是这个位置的节点是不存在的，因为不是所有的节点都存在，就是标准情况下，一个节点应该是有两个子节点的，一个左节点，一个右节点，但是不可避免的有的节点是没有左节点，或者是没有右节点的，这个时候我们不会不打印任何数据，而是使用N代替说明这个位置的节点不存在；

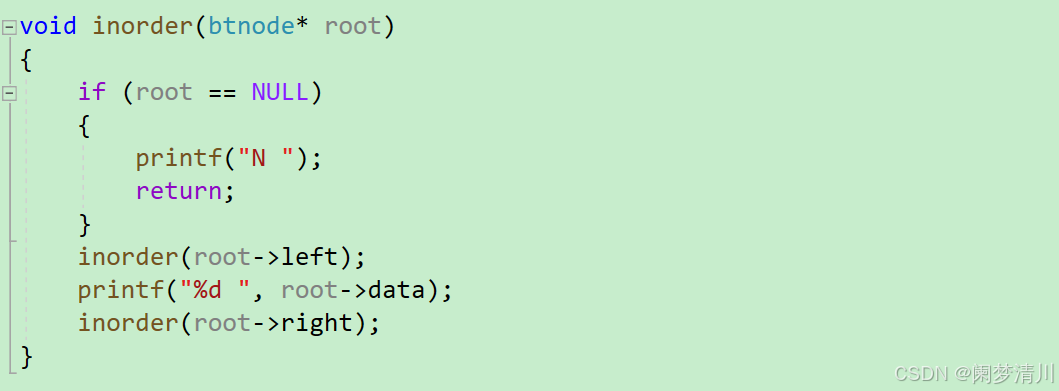
（4）中序遍历实现

这个就是先访问左边的节点，再访问根节点，最后访问右边的节点，没有字节点的就会打印N代替

（5）二叉树的节点个数

这个地方是使用的递归的方法，如果自己没有根节点，说明这个二叉树的节点的个数是0，否则就是用递归去进行节点个数的计算；

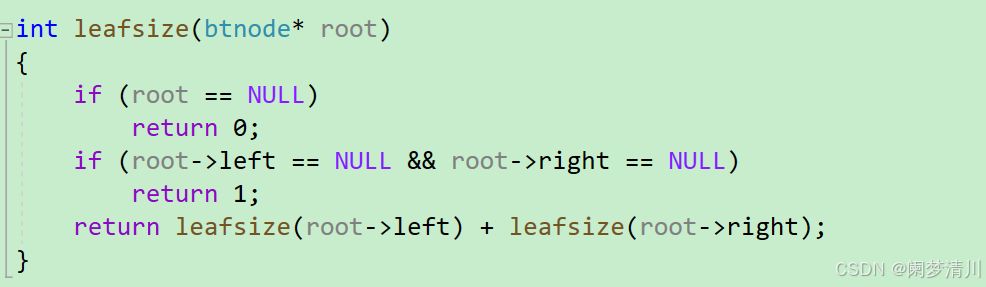
（6）二叉树树叶节点个数

这个也是分为有树根节点，没有树根节点，以及正常的使用递归进行计算的情况，这个时候使用递归进行计算就不需要加上1，因为上面的加1表示这个要加上树根节点，但是这个地方计算的是树叶节点，所以不需要加上1；

（7）二叉树的高度

这个地方是使用这个leftheight表示这个左子树的高度，rightheight表示这个右子树的高度，这个地方其实是可以直接写到返回值里面的，但是这个地方使用的是递归，如果不进行这个临时变量的定义而是直接写到这个return里面，这个调用的次数就会增加，放到oj里面运行就不会通过，显示这个运行时间过长，我们定义两个中间变量就可以去解决这个问题；

（8）二叉树节点的开辟

使用malloc函数开辟内存空间，需要包含对应的文件stdlib.h

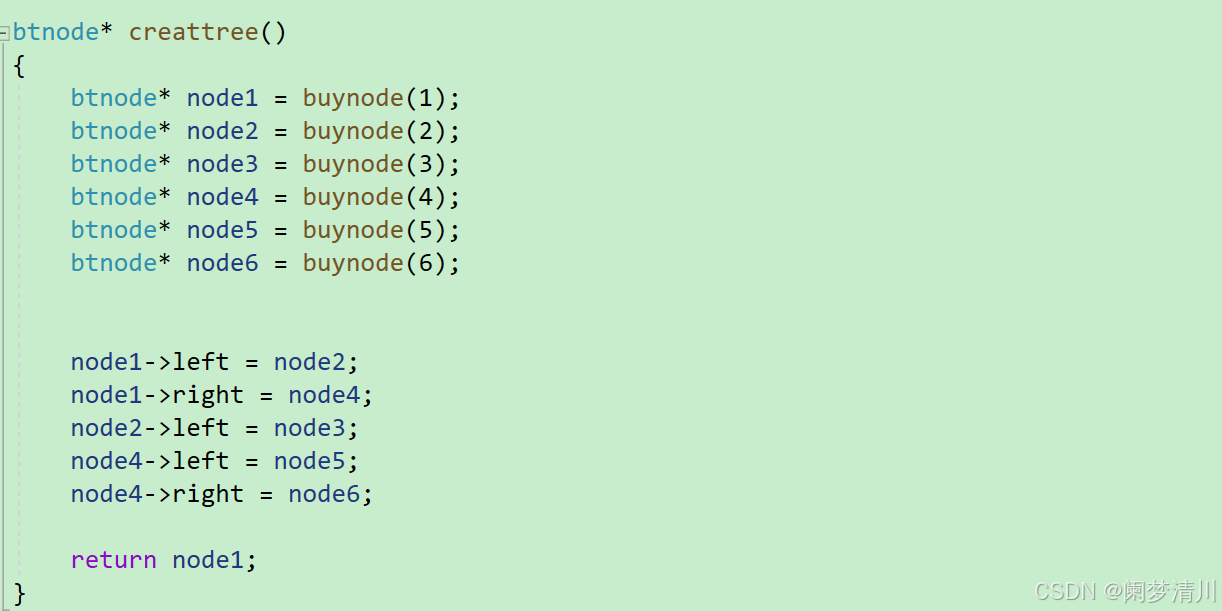
（9）建立一个测试二叉树

调用上面的buynode函数进行这个节点开辟，并建立不同的节点之间的连接关系，最后返回第一个节点；

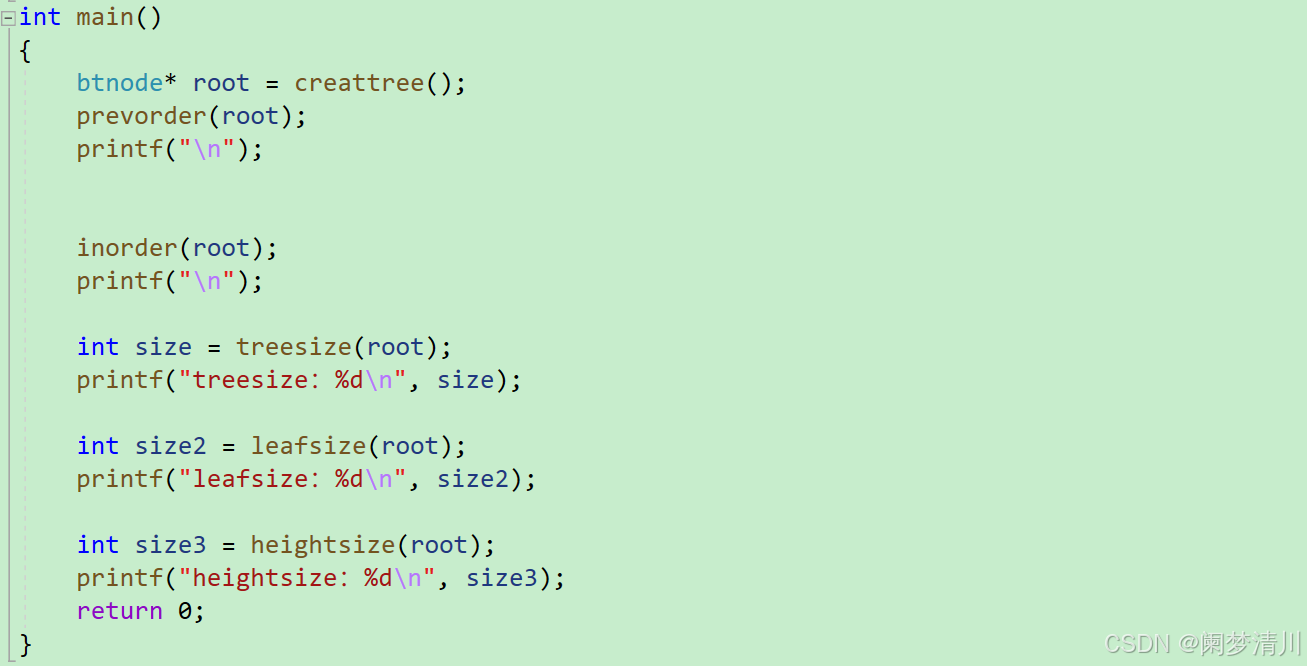
（10）测试二叉树相关函数的功能

打印输出这个二叉树的高度，节点个数，树叶节点个数进行这个功能的测试；

（11）第k层的数据个数

使用递归，把下一层即k-1层的左子树和右子树节点数量的和作为这个返回值；

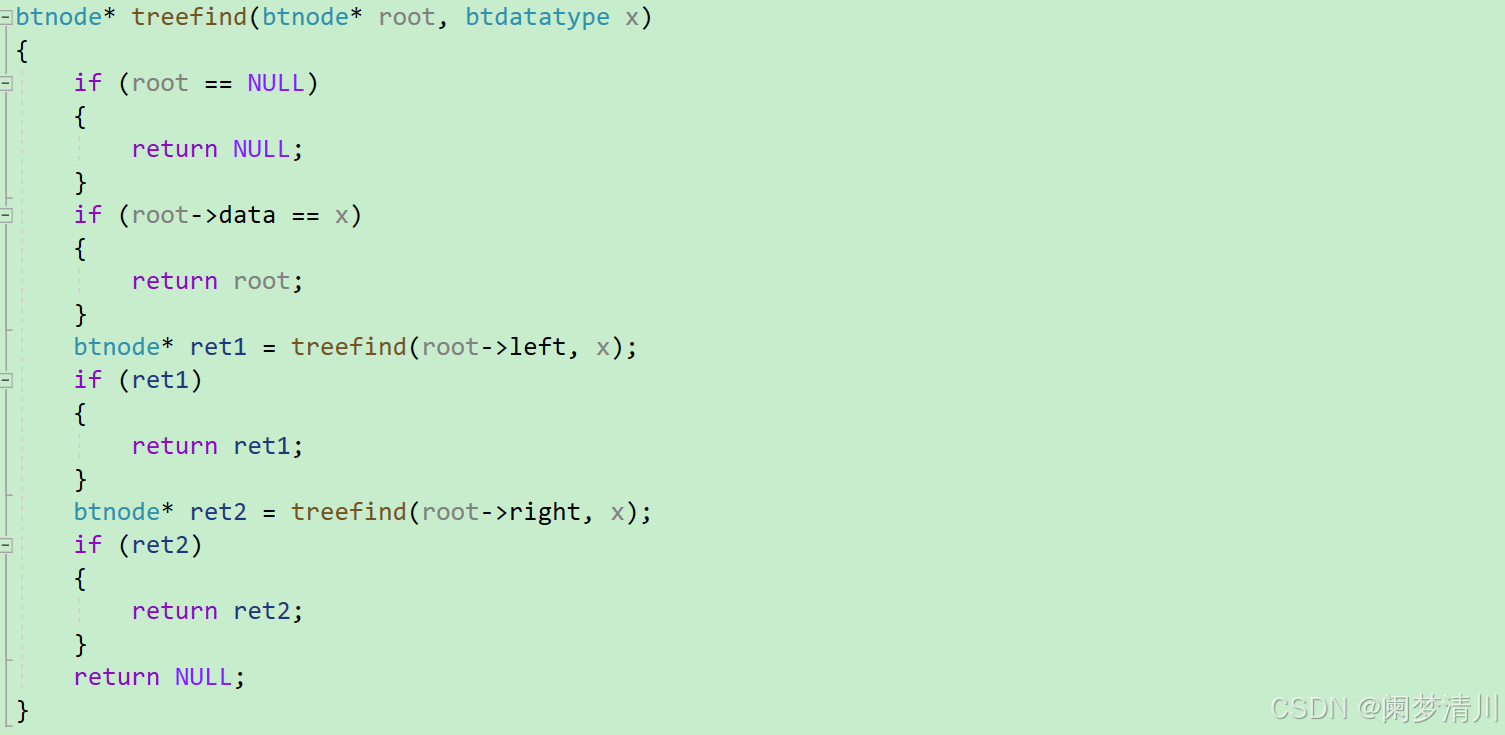
（12）二叉树里面查找节点

这个里面就是查找某一个特定的节点，这个节点作为返回值，我们定义两个临时变量作为左子树和右子树的返回值，如果左子树找到这个节点，我们就可以直接返回，否则的话，我们就需要去右子树去查找，找到这个节点后作为返回值，如果左子树，右子树找不到的话就返回NULL；

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
typedef int btdatatype;
typedef struct binarytreenode
{
	btdatatype data;
	struct binarytree* left;
	struct binarytree* right;
}btnode;
 
void prevorder(btnode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	printf("%d ", root->data);
	prevorder(root->left);
	prevorder(root->right);
}
 
void inorder(btnode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	inorder(root->left);
	printf("%d ", root->data);
	inorder(root->right);
}
 
 
int treesize(btnode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return treesize(root->left) + treesize(root->right) + 1;
}
 
int leafsize(btnode* root)
{
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
		return 1;
	return leafsize(root->left) + leafsize(root->right);
}
 
int heightsize(btnode* root)
{
	if (root == NULL)
		return 0;
	int leftheight = heightsize(root->left);
	int rightheight = heightsize(root->right);
	return leftheight > rightheight ? heightsize(root->left) + 1 : heightsize(root->right) + 1;
}
 
int treesizek(btnode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return treesizek(root->left, k - 1) + treesizek(root->right, k - 1);
}
 
//二叉树里面查找指定的节点
btnode* treefind(btnode* root, btdatatype x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	btnode* ret1 = treefind(root->left, x);
	if (ret1)
	{
		return ret1;
	}
	btnode* ret2 = treefind(root->right, x);
	if (ret2)
	{
		return ret2;
	}
	return NULL;
}
 
btnode* buynode(int x)
{
	btnode* node = (btnode*)malloc(sizeof(btnode));
	if (node == NULL)
	{
		perror("malloc fail");
		return;
	}
	node->data = x;
	node->left = NULL;
	node->right = NULL;
}
 
 
 
btnode* creattree()
{
	btnode* node1 = buynode(1);
	btnode* node2 = buynode(2);
	btnode* node3 = buynode(3);
	btnode* node4 = buynode(4);
	btnode* node5 = buynode(5);
	btnode* node6 = buynode(6);
 
 
	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;
 
	return node1;
}
int main()
{
	btnode* root = creattree();
	prevorder(root);
	printf("\n");
 
 
	inorder(root);
	printf("\n");
 
	int size = treesize(root);
	printf("treesize：%d\n", size);
 
	int size2 = leafsize(root);
	printf("leafsize：%d\n", size2);
 
	int size3 = heightsize(root);
	printf("heightsize：%d\n", size3);
 
	int size4 = treesizek(root,3);
	printf("treesizek：%d\n", size4);
	return 0;
}