【算法】单调队列

一、什么是单调队列

单调队列是一种数据结构，其特点是队列中的元素始终保持单调递增或递减，主要用于维护队列中的最小值或最大值。

不同于普通队列只能从队头出队、队尾入队，单调队列为了维护其特征，还允许从队尾出队

不管怎么向单调队列中添加元素或删除元素，其单调性始终不变。这是如何做到的呢？我们用一道例题来说明

二、如何使用单调队列

2.1 滑动窗口问题

滑动窗口问题是单调队列的典型应用场景

简单来说，一个长度固定的窗口从序列开始一步步移动到结尾，我们要得到这个窗口每一步移动中其内部的最大值和最小值。

这个问题很简单，如果我们使用一个单调队列，窗口每次移动就将新元素入队，让其内部的元素保持单调递增，那么队头元素就是窗口的最小值，求最大值则保持单调递减即可

那我们该如何维护一个单调队列呢？首先来讲讲单调队列的思想

2.2 单调队列的思想

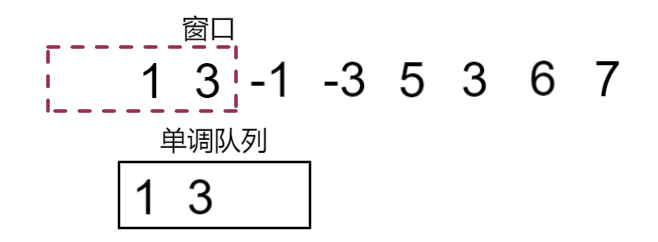
我们以上面例题中给出的序列 {1,3,-1,-3,5,3,6,7} 为例，窗口大小为3，单调队列大小和窗口一致

窗口从头开始向后移动，首先是1入队，然后是3入队，到这里单调队列内部都保持单调递增，于是我们不作处理

窗口继续向后移动，接下来是-1入队。但是-1入队后就打破了单调队列的单调性了，所以我们需要进行一些操作维护其单调性

因为我们选择保持队列单调递减，所以当有更小的元素要从队尾入队时，我们要把它前面所有比它更大的元素全都先从队尾出队。

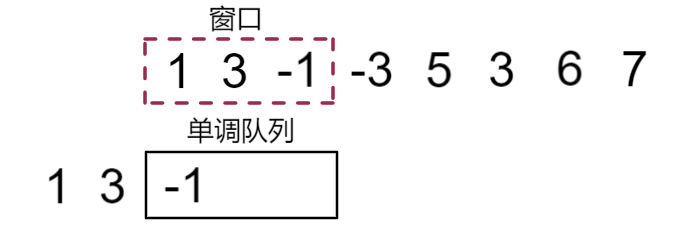
也就是说，当准备入队的元素更优时，我们需要先将前面造成干扰的元素出队，再将新元素入队。

此时，窗口已经完整的进入序列中了，可以开始拿到最值，此时单调队列的队头元素就是窗口中的最小值

窗口滑动，接下来-3准备入队。和前面的步骤一样，先将-1从队尾出队，然后-3入队

得到此时窗口最小值-3 

窗口滑动，接下来5正常入队

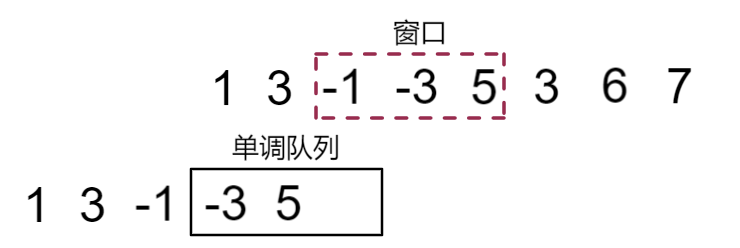
得到此时窗口最小值-3

窗口滑动，接下来3准备入队，和前面的步骤一样，先将5从队尾出队，然后3入队

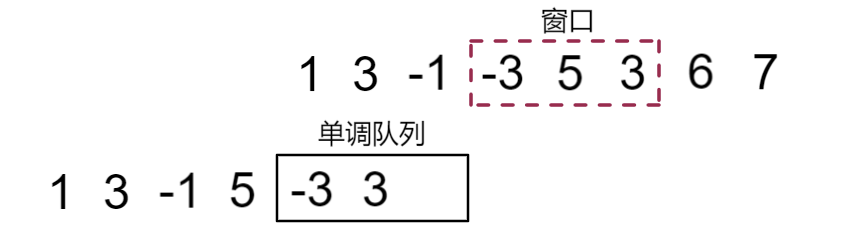
得到此时窗口最小值-3

窗口滑动，接下来6正常入队

但是！此时单调队列中的-3已经滑出窗口范围了，需要出队

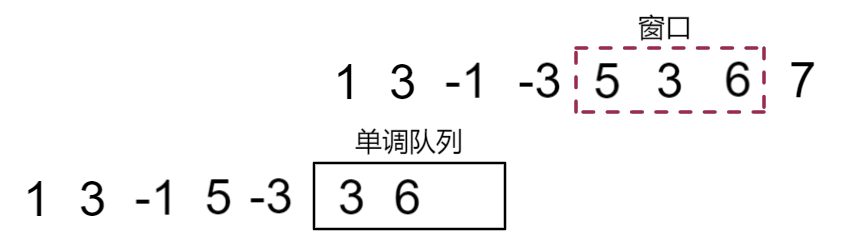
得到此时窗口最小值3

窗口滑动，接下来7正常入队

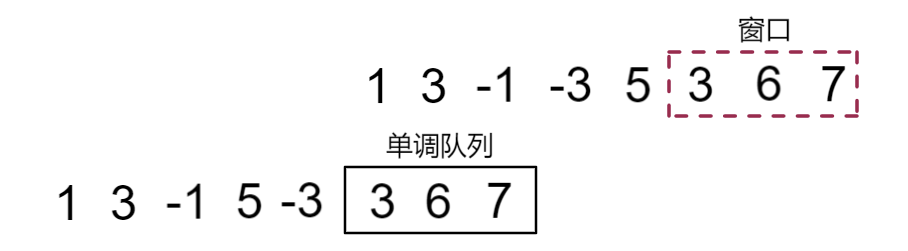
得到此时窗口最小值3

这就是单调队列完整的思想，如果要求窗口每个时刻的最大值，则将单调队列保持单调递减即可

关于单调队列还有一个很残酷的比喻：后入队的比先入队的年轻，如果后入队的既年轻又比先入队的更强，那先入队的就可以滚蛋了。就算先入队的更强，到了一定年龄之后也得滚蛋。

2.3 实际解题过程

明白了单调队列的思想后，我们还需要学会如何在实际解题时使用它

在上面的例题中，我们可以用一个数组来模拟单调队列，用两个下标 h 和 t 来维护队头和队尾

另外一个数组存储目标序列，len 表示窗口长度，i 表示窗口的右侧，则 i - len + 1就是窗口的左侧。通过i++就可以实现窗口滑动的效果

我们在单调队列中存储元素在原序列中的下标，这样做是为了便于判断一个元素仍在单调队列中但已经滑出窗口的情况（如果该元素的下标小于窗口左侧则说明已经滑出窗口，则出队）

用下标维护队列头尾的目的：采用伪删除法，将 t-- 就能达到队尾出队的效果，h++就能达到队头出队的效果

大概思路都讲完了，这里直接放出例题的代码

#include 
using namespace std;
 
const int N = 1000010;
 
int n, k;
int a[N];
int q[N];
 
void winmin() //求窗口最小值
{
    int h = 1, t = 0; //h是队头，t是队尾，队列初始为空
    for(int i = 1;i <= n;i++) //i为窗口右端，i递增则窗口不断滑动
    {
        while(h <= t && a[q[t]] >= a[i]) //队列不为空且队尾元素比新元素大，出队
            t--; 
        q[++t] = i; //存储下标方便判断队头出队
        if(q[h] < i - k + 1) h++; //队头存储的下标小于窗口左侧，队头元素滑出窗口
        if(i >= k) cout << a[q[h]] << " "; //打印窗口最小值
    }
    cout << endl;
}
 
void winmax() //求窗口最大值
{
    int h = 1, t = 0;
    for(int i = 1;i <= n;i++)
    {
        while(h <= t && a[q[t]] <= a[i])
            t--;
        q[++t] = i;
        if(q[h] < i - k + 1) h++;
        if(i >= k) cout << a[q[h]] << " ";
    }
    cout << endl;
}
 
int main()
{
    cin >> n >> k;
    for(int i = 1;i <= n;i++) //注意这里元素是从下标为1处开始存储
        cin >> a[i];
    winmin();
    winmax();
    return 0;
}

完.