《昇思25天学习打卡营第15天|Vision Transformer图像分类》

 随着基于自注意（Self-Attention）结构的模型的发展，特别是Transformer模型的提出，极大地促进了自然语言处理模型的发展。由于Transformers的计算效率和可扩展性，它已经能够训练具有超过100B参数的空前规模的模型。

ViT则是自然语言处理和计算机视觉两个领域的融合结晶。在不依赖卷积操作的情况下，依然可以在图像分类任务上达到很好的效果。

ViT（Vision Transformer）模型是由Google在2020年提出的一种用于图像分类的深度学习模型。它将图像处理问题转化为序列处理问题，借鉴了Transformer在自然语言处理中的成功经验。下面是ViT模型的详细结构和原理讲解：

1. 模型结构

ViT模型的主体结构是基于Transformer模型的Encoder部分（部分结构顺序有调整，如：Normalization的位置与标准Transformer不同），其结构图[1]如下：

ViT模型的结构包括以下几个主要部分：

1.1 输入分块（Patch Embedding）

• 输入图像：首先，将输入图像划分为固定大小的图像块（patch），例如，224x224的图像可以被划分为16x16的块，这样总共有196个块（patch）。
• 线性嵌入：然后，将每个图像块展平并通过一个线性投影层，得到每个块的嵌入表示。这个过程类似于将图像块转换为一个特征向量。

1.2 加入位置编码（Positional Encoding）

由于Transformer模型本身没有位置信息，ViT通过加入位置编码来提供图像块的位置信息。位置编码可以帮助模型识别每个图像块的位置，从而更好地捕捉空间关系。

1.3 Transformer Encoder

ViT的核心是多个Transformer Encoder层，每个Encoder层由以下几个部分组成：

• Multi-head Self-Attention（多头自注意力）：用于捕捉图像块之间的关系和依赖。
• Layer Norm（层归一化）：在多头自注意力和前馈神经网络之前和之后进行归一化。
• Feed Forward Neural Network（前馈神经网络）：由两个全连接层组成，用于非线性变换。

每个Transformer Encoder层会对输入的嵌入序列进行一系列的变换和计算，从而生成更高层次的特征表示。

1.4 分类头（Classification Head）

在最后一个Transformer Encoder层之后，会将第一个图像块的表示（通常称为[CLS]标记）输入到一个全连接层，进行分类。这个[CLS]标记用于聚合整个图像的信息。

2. 模型原理

Transformer基本原理

Transformer模型源于2017年的一篇文章[2]。在这篇文章中提出的基于Attention机制的编码器-解码器型结构在自然语言处理领域获得了巨大的成功。模型结构如下图所示：

其主要结构为多个Encoder和Decoder模块所组成，其中Encoder和Decoder的详细结构如下图[2]所示：

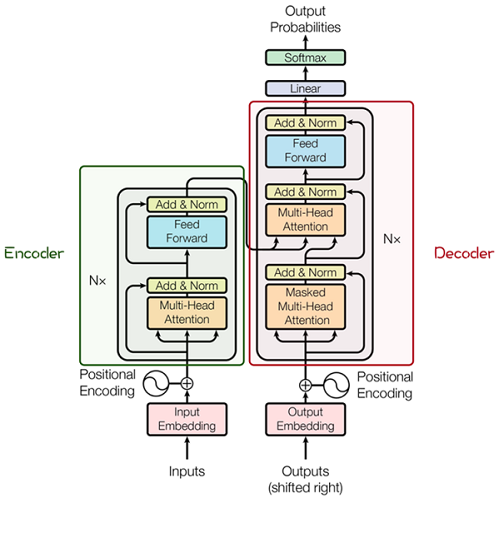
Encoder与Decoder由许多结构组成，如：多头注意力（Multi-Head Attention）层，Feed Forward层，Normaliztion层，甚至残差连接（Residual Connection，图中的“Add”）。不过，其中最重要的结构是多头注意力（Multi-Head Attention）结构，该结构基于自注意力（Self-Attention）机制，是多个Self-Attention的并行组成。

所以，理解了Self-Attention就抓住了Transformer的核心。

Attention模块 注意力模块 ¶

以下是Self-Attention的解释，其核心内容是为输入向量的每个单词学习一个权重。通过给定一个任务相关的查询向量Query向量，计算Query和各个Key的相似性或者相关性得到注意力分布，即得到每个Key对应Value的权重系数，然后对Value进行加权求和得到最终的Attention数值。

在Self-Attention中：

1. 最初的输入向量首先会经过Embedding层映射成Q（Query），K（Key），V（Value）三个向量，由于是并行操作，所以代码中是映射成为dim x 3的向量然后进行分割，换言之，如果你的输入向量为一个向量序列（𝑥1𝑥1，𝑥2𝑥2，𝑥3𝑥3），其中的𝑥1𝑥1，𝑥2𝑥2，𝑥3𝑥3都是一维向量，那么每一个一维向量都会经过Embedding层映射出Q，K，V三个向量，只是Embedding矩阵不同，矩阵参数也是通过学习得到的。这里大家可以认为，Q，K，V三个矩阵是发现向量之间关联信息的一种手段，需要经过学习得到，至于为什么是Q，K，V三个，主要是因为需要两个向量点乘以获得权重，又需要另一个向量来承载权重向加的结果，所以，最少需要3个矩阵。

1. 自注意力机制的自注意主要体现在它的Q，K，V都来源于其自身，也就是该过程是在提取输入的不同顺序的向量的联系与特征，最终通过不同顺序向量之间的联系紧密性（Q与K乘积经过Softmax的结果）来表现出来。Q，K，V得到后就需要获取向量间权重，需要对Q和K进行点乘并除以维度的平方根，对所有向量的结果进行Softmax处理，通过公式(2)的操作，我们获得了向量之间的关系权重。

1. 其最终输出则是通过V这个映射后的向量与Q，K经过Softmax结果进行weight sum获得，这个过程可以理解为在全局上进行自注意表示。每一组Q，K，V最后都有一个V输出，这是Self-Attention得到的最终结果，是当前向量在结合了它与其他向量关联权重后得到的结果。

通过下图可以整体把握Self-Attention的全部过程。

多头注意力机制就是将原本self-Attention处理的向量分割为多个Head进行处理，这一点也可以从代码中体现，这也是attention结构可以进行并行加速的一个方面。

总结来说，多头注意力机制在保持参数总量不变的情况下，将同样的query, key和value映射到原来的高维空间（Q,K,V）的不同子空间(Q_0,K_0,V_0)中进行自注意力的计算，最后再合并不同子空间中的注意力信息。

所以，对于同一个输入向量，多个注意力机制可以同时对其进行处理，即利用并行计算加速处理过程，又在处理的时候更充分的分析和利用了向量特征。下图展示了多头注意力机制，其并行能力的主要体现在下图中的𝑎1𝑎1和𝑎2𝑎2是同一个向量进行分割获得的。

2.Transformer Encoder

Transformer Encoder是由多个相同结构的编码器层堆叠而成，每个编码器层包括两个主要部分：Multi-Head Attention和前馈神经网络（Feed Forward Neural Network），并在这两者之间加上Layer Norm和Residual Connection。

3 位置编码（Positional Encoding）

由于自注意力机制对输入顺序不敏感，ViT通过位置编码来提供图像块的位置信息。位置编码可以是固定的，也可以是学习得到的。在实际应用中，通常使用正弦和余弦函数来生成固定的位置编码。

3.1 位置编码公式

位置编码可以使用正弦和余弦函数生成，这样的位置编码在不同位置具有唯一性，并且具有平滑的变化：

PE(pos,2i)=sin⁡(pos100002i/d)PE_{(pos, 2i)} = \sin\left(\frac{pos}{10000^{2i/d}}\right)PE(pos,2i)​=sin(100002i/dpos​) PE(pos,2i+1)=cos⁡(pos100002i/d)PE_{(pos, 2i+1)} = \cos\left(\frac{pos}{10000^{2i/d}}\right)PE(pos,2i+1)​=cos(100002i/dpos​)

其中，pospospos 表示位置，iii 表示维度索引，ddd 表示编码维度。

3.2 加入位置编码

在输入图像块嵌入（Patch Embedding）后，将位置编码与嵌入向量相加，形成最终的输入序列：

Efinal=Epatch+PEE_{final} = E_{patch} + PEEfinal​=Epatch​+PE

这样，输入序列不仅包含了图像块的特征表示，还包含了它们的位置信息。