【排序算法】插入排序（希尔排序）

目录

一.直接插入排序

1.基本思想

 2.实现

3.特性

1.效率

2.时间复杂度：O(N^2)

3.空间复杂度：O(1)

4.稳定性：稳定

二.希尔排序

1.基本思想

2.实现

3.特性

1.效率

2.时间复杂度：O(N^1.3)

​编辑

3.空间复杂度：O(1)

4.稳定性：不稳定

---

一.直接插入排序

1.基本思想

直接插入排序是一种简单的插入排序法，其核心思想是对一个已经有序的序列插入一个数据，该数据依次比较有序序列中的值，直到插入到合适的位置。在我们玩扑克牌整理牌序的时候，用到的就是直接插入排序的思想。

 2.实现

直接插入排序的实现原理如下动图所示：

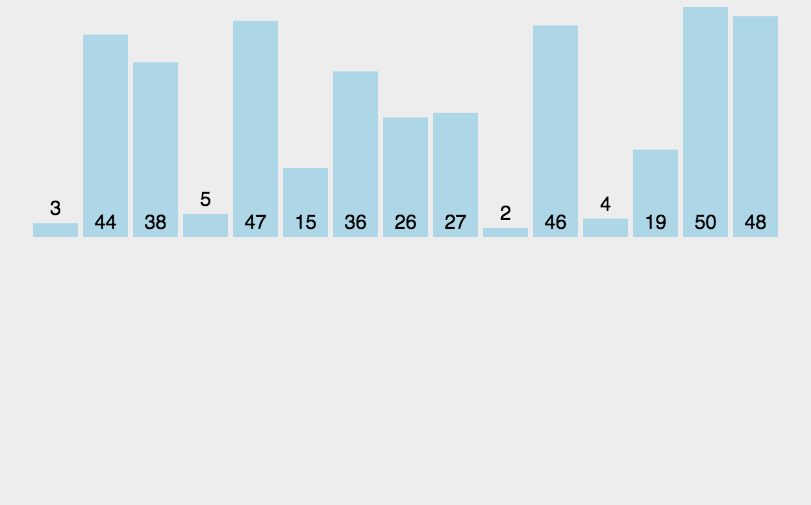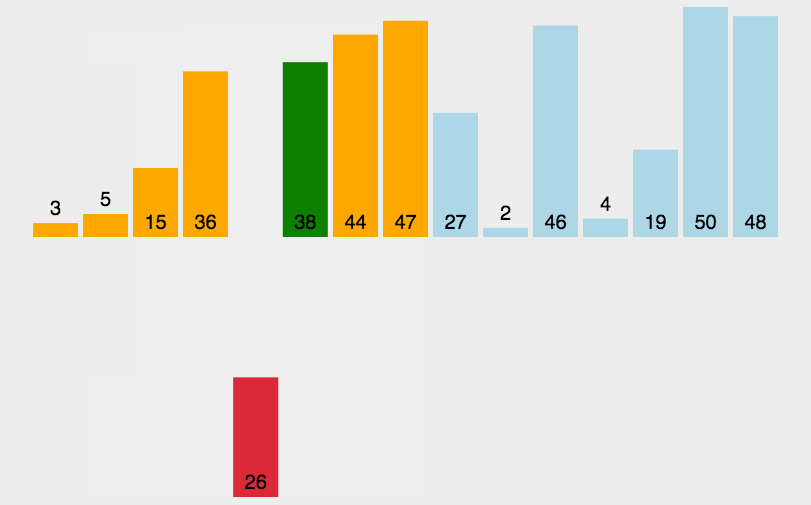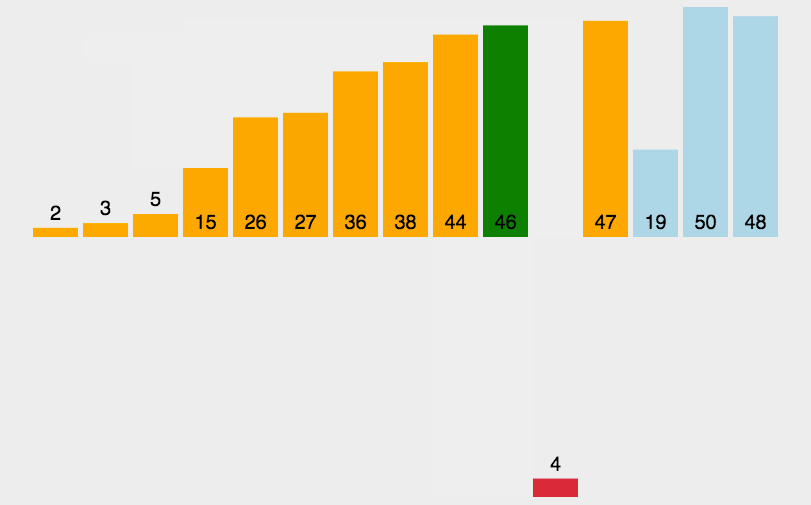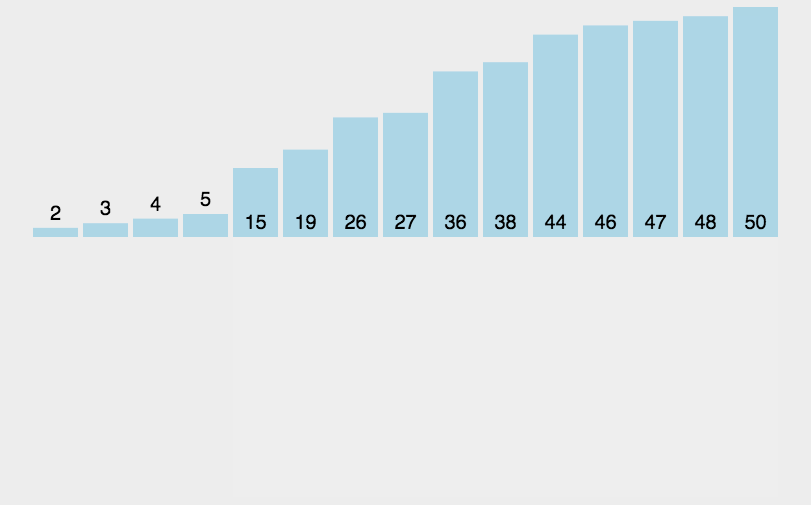
如上图所示，插入排序的前提是在一个已经有序的序列中进行插入，那么不妨假设在闭区间[0,end]中是有序的，那么插入元素在下标为end+1（用tmp存储）的位置开始插入，end+1和end的值进行比较，假设此时排升序，那么一旦end+1的值小于end，那么end的值就要向后移动，使end+1的值变为end就可（这里解释了为什么要用tmp存储end+1处的值，一旦被end替代，end+1的值就找不到了），当然，变换后end需要减1进行对下一个位置的比较，直到与0下标位置进行比较（此时end = 0）若不满足小于那么停止循环，直接在end+1的地方放置tmp即可。

值得注意的是，放置end+1为tmp必须要在循环外进行，这是由于边界问题，如下图所示插入2的情况：

void InsertSort(int* arr, int n)
{
	//[0,end]有序，end+1是插入值下标
	//最后一个插入的值下标为n-1,即end+1=n-1,end=n-2
	for (int i = 0; i < n - 1; i++)
	{
		int end = i;
		int tmp = arr[end + 1];
		while (end >= 0)
		{
			if (tmp < arr[end])
			{
				arr[end + 1] = arr[end];
				end--;
			}
			else
			{
				break;
			}
		}
		arr[end + 1] = tmp;
	}
}

3.特性

1.效率

元素越接近有序，直接插入排序算法的时间效率就越高，完全是逆序时效率最低

2.时间复杂度：O(N^2)

最好情况下序列为顺序，每个end+1只需要与前一个判断即可，此时时间复杂度为O（N）

最坏情况下序列为逆序，此时每个end+1都要换到下标为0为止，此时时间复杂度为O(N^2)

3.空间复杂度：O(1)

直接插入排序没有额外的空间开销，因此空间复杂度为O(1)

4.稳定性：稳定

二.希尔排序

1.基本思想

根据直接插入排序元素越接近有序，直接插入排序算法的时间效率就越高 的特性，希尔排序运营而生，希尔排序的核心思想就是优化直接插入排序，先对序列进行预排序，将逆序的状态破坏，达到一定的有序程度再进行直接插入排序，这就是希尔排序。

2.实现

定义gap(间隔）为一个具体的数，图中为3，那么整个序列将被分为gap组，分别对每组进行直接插入排序，就如图中黄红绿代表的三组一样，如此就能将一个“较为逆序”的序列变为“较为有序”，就像9这个最大的数一下就换到了最后一个位置，这样再进行插入排序，效率就会大大提高。

 其中对一组的插入排序写起来十分简单，只需要将直接插入排序的减1的操作改为减gap，加1改为gap即可，也就是说是上文插入排序的推广情况。然后再套上一个gap组的循环，就能实现预排序，注意要将第二层循环内改为i = j，不要只加个外层循环就完了。

void SheerSort(int* arr, int n)
{
	int gap = 3;
 
	//总共有gap组，每组都进行插入排序
	//注意i = j，每组的开始不同
	for (int j = 0; j < gap; j++)
	{
		//一组的插入排序
		//注意end+gap是插入值下标，i
		for (int i = j; i < n - gap; i += gap)
		{
			int end = i;
			int tmp = arr[end + gap];
			while (end >= 0)
			{
				if (tmp < arr[end])
				{
					arr[end + gap] = arr[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			arr[end + gap] = tmp;
		}
	}
	
	//最后进行直接插入排序
	InsertSort(arr, n);
}

当然也可以直接多组排序同时进行，这样就少套了一层循环，但执行的总次数和上述代码是相同的，也就是说效率依然是相同的。该循环直接从第一个数到下标为n-gap-1的值，该下标+gap即是最后一个值。 

void SheerSort(int* arr, int n)
{
	int gap = 3;
 
	//多组同时进行
	for (int i = 0; i < n - gap; i++)
	{
		int end = i;
		int tmp = arr[end + gap];
		while (end >= 0)
		{
			if (tmp < arr[end])
			{
				arr[end + gap] = arr[end];
				end -= gap;
			}
			else
			{
				break;
			}
		}
		arr[end + gap] = tmp;
	}
 
 
	//最后进行直接插入排序
	InsertSort(arr, n);
}

3.特性

1.效率

希尔排序是对直接插入排序的优化，当gap>1时就是预排序，目的是让数组更接近有序的状态，从而方便gap=1时的直接插入排序，提高效率。其中gap的取值方法有很多，但没有人证明哪种取值方法效率最高，以下出自《数据结构-用面相对象方法与C++描述》--- 殷人昆

2.时间复杂度：O(N^1.3)

由于gap取值不同，时间复杂度也不相同，但可以大概估算个平均结果是O（N^1.3）

以下内容出自《数据结构(C语言版)》--- 严蔚敏

3.空间复杂度：O(1)

希尔排序没有额外的空间开销，因此空间复杂度为O(1)

4.稳定性：不稳定