【算法刷题 | 动态规划14】6.28（最大子数组和、判断子序列、不同的子序列）

35.最大子数组和

35.1题目

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组

是数组中的一个连续部分。

• 示例一：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 

• 示例二：

输入：nums = [1]
输出：1

35.2解法：动规

35.2.1动规思路

1. 确定dp数组以及下标含义：

   dp[i]：下标为i的子数组的最大子数组和为dp[i]

2. 确定递推公式：dp[i]=Math.max( dp[i-1]+nums[i]，nums[i])

3. dp数组初始化：dp[0]=Math.max(0,nums[i])

4. 确定遍历顺序：从前往后

5. 举例推导：

   

35.2.2代码实现

	public int maxSubArray(int[] nums) {
        int[] dp=new int[nums.length];
        int result=nums[0];
        dp[0]=nums[0];
        for(int i=1;i<nums.length;i++){
            dp[i]=Math.max(dp[i-1]+nums[i],nums[i]);
            result=Math.max(result,dp[i]);
        }
        return result;
    }

36.判断子序列

36.1题目

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

进阶：

如果有大量输入的 S，称作 S1, S2, … , Sk 其中 k >= 10亿，你需要依次检查它们是否为 T 的子序列。在这种情况下，你会怎样改变代码？

• 示例一：

输入：s = "abc", t = "ahbgdc"
输出：true

• 示例二：

输入：s = "axc", t = "ahbgdc"
输出：false

36.2解法：动规

36.2.1动规思路

1. 确定dp数组以及下标含义:

   dp(i)(j)：表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同的子序列的长度为dp(i)(j)

2. 确定递推公式：

   2.1 s[i-1]=t[j-1]：t中找到了一个字符，在s中也出现，即dp(i)(j)=dp(i-1)(j-1)+1

   2.2 s[i-1]!=t[j-1]：t下标j-1位置的字符和s下标i-1位置的字符不同，即dp(i)(j)=dp(i)(j-1)

3. dp数组初始化：dp(i)(0)和dp(0)(j)位置的元素没有意义

4. 确定遍历顺序：从上到下

5. 举例推导：

   

36.2.2代码实现

	public boolean isSubsequence(String s, String t) {
        int[][] dp=new int[s.length()+1][t.length()+1];
        for(int i=1;i<=s.length();i++){
            for(int j=1;j<=t.length();j++){
                if(s.charAt(i-1)==t.charAt(j-1)){
                    dp[i][j]=dp[i-1][j-1]+1;
                }else{
                    dp[i][j]=dp[i][j-1];
                }
            }
        }
        return dp[s.length()][t.length()]==s.length();
    }

37.不同的子序列

37.1题目

给你两个字符串 s 和 t ，统计并返回在 s 的 子序列 中 t 出现的个数，结果需要对 109 + 7 取模。

• 示例一：

输入：s = "rabbbit", t = "rabbit"
输出：3
解释：
如下所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
rabbbit
rabbbit
rabbbit

• 示例二：

输入：s = "babgbag", t = "bag"
输出：5
解释：
如下所示, 有 5 种可以从 s 中得到 "bag" 的方案。 
babgbag
babgbag
babgbag
babgbag
babgbag

37.2解法：动规

37.2.1动规思路

1. 求解：求子序列s组装成t的几种方法！！！

2. 确定dp数组以及下标含义：

   dp(i)(j)：以下标i-1为结尾的s子序列中 出现 以下标j-1为结尾的t子序列的个数 为dp(i)(j)

3. 确定递推公式：

   3.1 s[i-1]=j[j-1]：两种情况，取s[i-1]或不取，即dp(i)(j)=dp(i-1)(j-1)+dp(i-1)(j)

   3.2 s[i-1]!=[j-1]：只能不取s[i-1]，即dp(i)(j)=dp(i-1)(j)

4. dp数组初始化：

   dp(i)(0)：子序列s组装成空串的方法肯定有一种

   dp(0)(j)：无意义

5. 确定遍历顺序：从上到下

6. 举例推导：

   

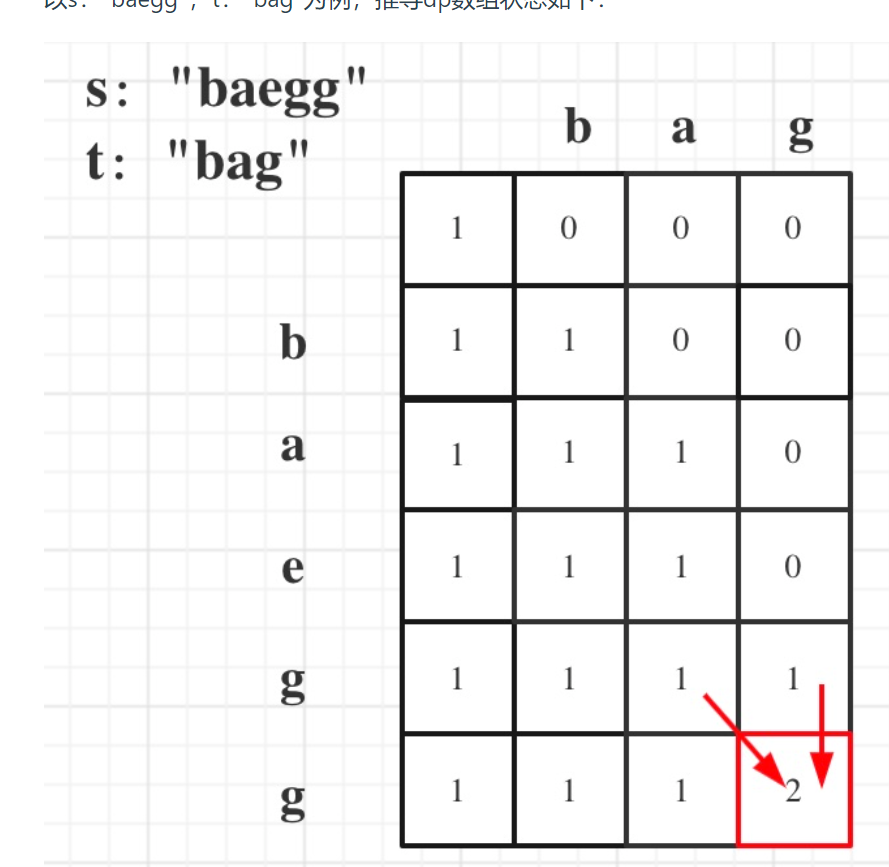
37.2.2代码实现

	public int numDistinct(String s, String t) {
        int[][] dp=new int[s.length()+1][t.length()+1];
        //初始化
        for(int i=0;i<=s.length();i++){
            dp[i][0]=1;
        }
        for(int i=1;i<=s.length();i++){
            for(int j=1;j<=t.length();j++){
                if(s.charAt(i-1)==t.charAt(j-1)){
                    //两种情况：取/不取
                    dp[i][j]=dp[i-1][j-1]+dp[i-1][j];
                }else{
                    dp[i][j]=dp[i-1][j];
                }
            }
        }
        return dp[s.length()][t.length()];
    }