-
【论文阅读】-- 时间空间化:用于深度分类器训练的可扩展且可靠的时间旅行可视化

Temporality Spatialization: A Scalable and Faithful Time-Travelling Visualization for Deep Classifier Training

摘要
时间旅行可视化回答了深度分类器的预测是如何在训练过程中形成的。它在二维或三维空间中可视化分类边界和样本嵌入在训练过程中如何演变。
在这项工作中,我们提出了 TimeVis,一种用于深度分类器的新型时间旅行可视化解决方案。与最先进的解决方案 DeepVisualInsight (DVI) 相比,TimeVis 可以显着 (1) 减少渲染样本跨不同训练时期的可视化错误,(2) 提高可视化效率。为此,我们设计了一种称为时间空间化的技术,它将空间关系(例如,单个历元中的相邻样本)和时间关系(例如,相邻训练历元中的一个相同样本)统一为一个高维拓扑复合体。这种时空复合体可用于有效地训练一种可视化模型,以准确地投影和逆投影跨时期的任何高维和低维数据。我们的大量实验表明,与 DVI 相比,TimeVis 不仅能够更准确地保留可视化的时间旅行语义,而且可视化效率快 15 倍,实现了时间旅行可视化的新的最先进技术。1 引言
时间旅行可视化是解决训练过程中如何形成深层模型预测的解决方案,正在成为可解释人工智能的一个新分支[Yang et al., 2022c]。这种可视化展示了如何在训练过程中学习高维分类景观,这可以促进基于训练的嵌入生成因果推理[Mallick et al., 2019]和主动学习算法[Sener and Savarese, 2017]。
任何深度分类器的时间旅行可视化解决方案都需要满足三个空间属性和一个时间属性,以便忠实地反映高维分类景观的动态[Yang et al., 2022c]。简而言之,给定一组在 epoch et 中训练的高维表示,三个空间属性是:
- 邻居保留属性:任何高维表示的邻居在投影到可见的低维空间后都应该被保留。
- 边界距离保留属性:从任何高维表示到其最近的分类边界的相对距离在投影到可见的低维空间后被保留。
- 逆投影保留属性:将高维表示 x 投影到低维空间作为 y 后,我们将 x 逆投影回高维空间作为 x′,使得 x 和 x′ 相似。
此外,单一时间属性要求:
- 时间保留属性(连续性):如果高维表示 xt+k(来自历元 t + k)的邻居与其对应 xt(来自历元 t)变化不大,则它们的低维投影 yt+k 和yt 应该很接近。
这些属性确保模型训练过程的“动画”可以在可见的低维空间中反射性地(由于空间属性)和平滑地(由于时间属性)“播放”。
DeepVisualInsight (DVI) 作为最先进的技术,是为了实现这些特性而进一步结晶的[Yang et al., 2022c]。从技术上讲,DVI 将可视化模型训练为几个强制属性的损失函数的自动编码器。然而,该解决方案在可视化可扩展性和跨不同时代的样本移动语义的忠实度方面存在局限性。
问题 1:可视化可扩展性。考虑到分类景观在一个时期与另一个时期不同,时间旅行可视化通常是一种记录和重放技术,用于记录和可视化每个时期中部分训练的分类器。 DVI 在每个时间步上训练一个可视化模型。因此,可视化训练过程的成本可能会非常高,尤其是当训练周期数很大时。实验表明,在普通 GPU 工作站上训练一个可视化模型大约需要 15 分钟 [Yang et al., 2022c],这表明训练 100 个 epoch 的可视化模型大约需要 24 小时。更糟糕的是,为了满足时间属性,训练 epoch et 分类器的可视化模型需要 epoch et−1 可视化模型的可用性,这限制了其并行潜力。
问题 2:旅行语义的忠实度(可视化错误)。当我们投影样本 X = {x1, x2,… 的学习表示时。 。 。 , xw}(xi 表示第 i 个 epoch 的样本表示)按时间顺序到低维空间,它们的投影 Y = {y1, y2, . 。 。 , yw} 形成行进轨迹。当我们在二维画布上观察 yi 到 yi+1 的移动时,可能是由(1)高维空间中从 xi 到 xi+1 的实际移动和(2)可视化扰动或错误引起的。我们将后者引起的运动称为样本的不忠实运动。可视化模型被训练为 V = ⟨φ, ψ⟩,其中 φ 将高维点投影到低维空间,ψ 将低维点逆投影回高维空间。 DVI 通过在第 i 时期的可视化模型进行重新训练,在第 i + 1 时期训练可视化模型 V = ⟨φ, ψ⟩。随机性诱导的再训练过程不可避免地会产生无意的波动,以可视化分类景观。此外,DVI中设计的时间损失可以冻结少数动态样本,而大多数样本在高维空间中不移动。因此,可视化的旅行语义不能很好地真实反映高维空间的动态。
在这项工作中,我们提出 TimeVis 通过一种称为时间空间化的技术来统一解决上述问题。与 DVI 为每个部分训练的分类器训练可视化模型相比,我们训练可视化模型来捕获所有分类器的表示嵌入。具体来说,我们的方法“空间化”样本的时间关系及其在其他时期的对应关系。在 TimeVis 中,我们认为每个表示都有空间邻居和时间邻居。从技术上讲,我们(1)收集训练期间出现的所有表示,(2)构建一个时空复合体来捕获同一高维空间中表示的空间和时间关系,以及(3)学习维度投影和逆向表示基于这种复杂的投影。为了进一步提高可视化的可扩展性,我们提出了一种时空复合体的复合体缩减技术,它可以成功地压缩复合体的大小,而不会影响太多的可视化精度。
我们对各种数据集的实验表明,与 DVI 相比,TimeVis 可以 (1) 显着提高训练可扩展性(快 15 倍),(2) 大大提高旅行忠实度,以及 (3) 在其他空间属性上实现可比的性能。
总之,这项工作做出了以下贡献:
- 我们发现了限制新兴时间旅行可视化的实际适用性的两个关键问题。
- 我们提出时间空间化来显着提高旅行语义的可视化可扩展性和可视化忠实度,实现时间旅行可视化的新的最先进技术。
- 我们基于我们的技术构建了一个工具TimeVis 以支持其实际使用,该工具可在[Yang et al., 2022b] 和https://github.com/yanglinyang/TimeVis 上公开获取。
2 动机
图 1 显示了在 CIFAR10 数据集上训练 ResNet18 时 DVI 在训练后期的时间旅行可视化结果。在后期,分类器的语义收敛。一般来说,损失、训练精度和测试精度不会改变。就个体而言,几乎所有训练样本的表示都保留了这些时期中的 k 个最近邻。

然而,DVI 有两个可视化错误,可能会影响对分类情况的理解。首先,在中间创建一个绿色区域(即鸟类类别),位于第 99 纪元到第 100 时期的红色区域(即猫类别)附近。然而,落在这个新绿色区域中的鸟类样本是不接近表示空间中的猫图像样本。其次,我们进一步观察画布上样本的一些错误波动。样本在四个时期内来回移动,如图 1 所示。相反,它的表示和邻居在高维空间中的各个时期都保持不变。噪声可视化扰动可能会误导用户怀疑训练的稳定性,并误解高维空间中到底发生了什么。由于空间限制,我们还在 [Yang et al., 2022b] 上通过 DVI 在画布上展示了一个“冻结”的样本,其中样本在高维空间中非常动态。
3 问题定义
给定 d 维空间中的数据集 D = {s1, s2, …, sn}(n 是数据集大小),一组类 C = {c1, c2, …, cm}(m 是数量类大小),我们有一个 w 个深度分类器的序列 f 1(·), f 2(·), 。 。 。 , f w(·) 按时间顺序排列,其中每个 f t : Rd → Rm 是训练时期 et 的学习分类器。我们假设每个深度分类器 f t(·) 可以分解为特征函数 gt : Rd → Rr 和预测函数 ht : Rr → Rm (即 f t = ht ◦ gt),其中 r 是表示空间的维度。因此,我们可以导出一组样本表示 Xt = {xt1, xt2,…。 。 。 , xtn} 对于每个时期 t,其中 xt i = gt(si) ∈ Rr。请注意,我们使用上标和下标分别表示不同的时间步长和不同的样本。样本 si 在不同时间步长的学习表示表示为 Xi = {x1 i , x2 i ,…。 。 。 ,xw我}。
我们的目标是一种可视化模型 V = ⟨φ, ψ⟩,其中 φ : Rr → Rl 和 ψ : Rl → Rr (l ∈ {2, 3} 是可见低维空间的维度)。给定可视化解 V = ⟨φ, ψ⟩,我们 (1) 在可见的低维空间中将每个表示 xt i 可视化为 yt i = φ(xt i); (2)通过 c = arg maxc∈C ht(ψ(y)) 在画布上绘制任意点 y ∈ Rl 来形成分类景观。此外,不自信的区域(即决策边界)被着色为白色。此外,我们要求 V = ⟨φ, ψ⟩ 满足三个空间属性(即邻居保留属性、边界距离保留属性和逆投影保留属性)和一个时间属性 [Yang et al., 2022c]。
4 方法论
概述 图 2 显示了 TimeVis 解决方案的概述。在高维空间中,我们考虑表示的超集 X = X1 ∪ X2 ∪ … ∪ Xw。对于每个样本 xt i ∈ X,我们定义它的 k 个空间邻居和 k 个时间邻居。 xt i 的时间邻居的示例可以是 xt+1 i 或 xt−1 i,即下一个或上一个时期中的相同自身。通过这种方式,时间信息被“空间化”。与空间邻居相反,时间邻居可以捕获跨时期高维空间中样本的动态。此外,时间和空间邻居现在具有可比性,这使我们能够进一步捕获不同时期下不同样本的关系。
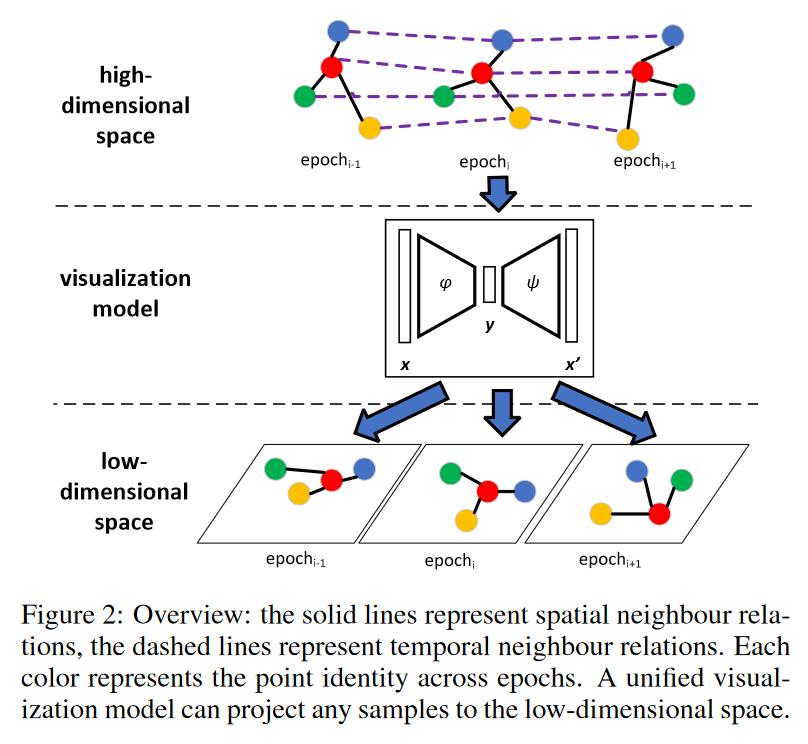
基于定义的邻近关系,我们为 X 建立一个统一的时空复合体。自然地,我们只需要一个可视化模型 V = ⟨φ, ψ⟩ 来投影在 x ∈ X ⊂ Rr 和 y ∈ Y ⊂ Rl 之间。请注意,根据 c = arg maxc∈C ht(ψ(y)),低维空间中的相同位置 y 在不同的历元 t 中可能具有不同的颜色(即预测)。在这项工作中,我们使用自动编码器架构来实现 V 。由于时间关系已经空间化,自动编码器只需要基于与三个空间属性相对应的损失函数进行训练(参见附录 A [Yang et al., 2022a])。
4.1 时空复合体
空间邻居 给定 Xt 和 Xt 上定义的距离度量,d(·):Rr×Rr → R≥0(例如,欧几里德距离),我们定义 xt i 的 k 空间邻居 N S k (xi) = argminJ ⊂Xt{xt i},|J |=k P xt j∈J d(xt j , xt i) 作为其 k 个空间邻居。
时间邻居 给定一个超集 X = X1 ∪ X2 ∪ · · · ∪ Xn 和在 X 上定义的距离度量,d(·)。对于给定的 xt i ∈ Xi,我们将其 k 个最近的时间邻居表示为 N T k (xt i) = argminJ ⊂Xi{xt i},|J |=k P xt′ i ∈J d(xt′ i , xt我 )。
给定一个嵌入 xt i ∈ Xi,我们使用大小为 W 的时间滑动窗口来描述其时间谱。换句话说,我们从集合 X′ i = {max(1, xt− W 2 i ), … 中找到它的 k 个时间邻居 N T k (xt i) 。 。 。 , xt 我, . 。 。 , min(N, xt+ W 2 i })。这里,W是偶数正整数,阈值k和W是用户定义的值。
时空复合体 给定通用超集 X = X1 ∪ X2 ∪ · · · ∪ XT ,我们将时空复合体构建为图 Gst = ⟨X, Es ∪ Et⟩ 其中
- 空间关系集为 Es = {(xt i, xt j )|xt i, xt j∈ Xt, (xt i ∈ NS k (xt j ) 或 xt j ∈ NS k (xt i ))}
- 时间关系关系集为 Et = {(xtl i , xtm i )|xtl i , xtm i∈ X, (xtl i ∈ NT k (xtm i ) 或 xtm i ∈ NT k (xtm i ))}。
对于任意 e = (xtl i , xtm j ) (e ∈ Es ∪ Et),我们将其边权重指定为流形 M 上的相似性pitl jtm(定义参见附录 B)。
对于任意 e = (xtl i , xtm j ) (e ∈ Es ∪ Et),我们将其边权重指定为流形 M 上的相似性pitl jtm(定义参见附录 B)。低维空间,并根据与三个空间属性相对应的损失函数调整模型。
4.2 复数约简
当历元数 w 和数据集大小 n 很大时,在超大型时空复合体上训练可视化模型的成本极高。数据集大小 n 通常远大于历元数 w(即 n ≫ w),这意味着训练障碍在于 n。
时空复合体 Gst 也可以写为 Gst = ⟨X1 ∪ X2 ∪ · · · ∪ Xw, (Es1 ∪ Es2 ∪ · · · ∪ Esw ) ∪ Et⟩,其中每个 Est (t ∈ [1, w] )表示epoch et中的空间邻近关系,Et表示epoch之间的时间邻近关系[1,w]。我们将 Gt = ⟨Xt, Est ⟩ 表示为 epoch et 的空间复合体。从复杂结构的角度来看,减小每个Xt的尺寸可以有效地导致Est和Et的尺寸减小。反过来又降低了培训成本。在他的工作中,我们将复杂结构简化为算法1。即,我们根据复杂结构和缩减尺寸来缩减每个空间复合体(第1-3行)。然后,我们在简化的空间复合体之间建立时间关系(第 5-7 行)。
空间复数约简 给定一个空间复数 Gs = ⟨X, E⟩,我们的目标是将其简化为 G′s = ⟨X′, E′⟩,以便 (1) Gs 和 G′s 可以共享尽可能多的空间拓扑结构可能且 (2) ||X| − |X′||可以最大化。前者保证了G’s对于Gs的代表性,后者保证了后续复杂构建和模型训练的效率。在这项工作中,我们通过 Gs 和 G’s 的持久同源性来估计它们之间的拓扑相似性。为了自我遏制,我们提供了持久同源性的简要解释。读者可以参考[Chazal et al., 2015; Moor 等人,2020]了解更多详细信息。
持久同源性是拓扑数据分析(TDA)中的一个概念,它描述了给定点集 X 上的拓扑特征,其中可以评估任意点对的距离。在拓扑学中,单纯形代表点、三角形、四面体等高维拓扑结构。单纯复形K由一组单纯形组成。令 KX 为由 X 上所有单纯形组成的通用集合,过滤是 KX 上关于基于距离的条件 C 的一系列单纯形复形,因此:
- 给定距离 a,C 可用于对单纯形 Ka ⊂ KX 的子集进行切片。例如,长度 l ≤ a 的线段(超空间中的 1-单纯形)可以选择为 Ka。
- 对于任何 a ≤ b,Ka ⊆ Kb。
具体来说,过滤F = {Ka ⊂ KX : a ε R≥0}。给定 Ka ∈ F ,我们可以根据其单纯形导出拓扑特征(例如,空洞)。例如,可以通过连接一组单纯形来构造拓扑空洞,其中每个单纯形 x ∈ Ka。因此,在 X 上,拓扑特征 π 可以在出生距离处出现,在死亡距离处消失,记为 lif e(π) = (abirth, adeath)。我们定义 X 上的持久同源性来跟踪 X 上所有拓扑特征的寿命。持久图是持久同源性的表示,其中拓扑特征的寿命表示为平面中的点/线。
给定来自同一度量空间 X 的两个紧凑子集 X 和 X′,它们的持久图 DX 和 DX′ 的瓶颈距离 db(DX , DX′ ) 被证明满足以下约束 [Chazal et al., 2016; Chazal 等人,2014]:
d b ( D X , D X ′ ) ≤ 2 d H ( X , X ′ ) ( 1 ) d_b(\mathcal{D}_X,\mathcal{D}_{X'})\leq2d_H(X,X')\qquad(1) db(DX,DX′)≤2dH(X,X′)(1)来自同一度量空间 (X, d) 的 X 和 X′ 之间的豪斯多夫距离 dH 为:
d H = max { max x ∈ X min x ′ ∈ X ′ d ( x , x ′ ) , max x ′ ∈ X ′ min x ∈ X d ( x , x ′ ) } ( 2 ) d_{H}=\max\{\max_{\mathbf{x}\in\mathbf{X}}\min_{\mathbf{x}^{\prime}\in\mathbf{X}^{\prime}}d(\mathbf{x},\mathbf{x}^{\prime}),\max_{\mathbf{x}^{\prime}\in\mathbf{X}^{\prime}}\min_{\mathbf{x}\in\mathbf{X}}d(\mathbf{x},\mathbf{x}^{\prime})\}\qquad(2) dH=max{x∈Xmaxx′∈X′mind(x,x′),x′∈X′maxx∈Xmind(x,x′)}(2)
因此,豪斯多夫距离 dH (X, X’) 充当 db(DX , DX’ ) 的上限。因此,我们可以将空间复数约简问题转化为搜索问题,以找到 X′ ⊂ X,使得 (1) dH (X, X′) 最小化,并且 (2) ||X|− |X′||被最大化。在这项工作中,我们设计了一种类似于 k 中心问题 [Farahani 和 Hekmatfar,2009] 的贪婪下采样算法来解决该问题。贪心下采样算法 给定半径 r,我们将 B(x, r) 表示为以 x 为中心、半径为 r 的球,其中 x ∈ X。我们将问题简化为 X′ 的搜索问题,其中 |X′|最小化,使得 S x′ i∈X′ B(x′ i, r) 可以覆盖 X,这被称为 NP-hard。因此,我们设计了一种贪婪下采样算法来实现次优子集 X′,如算法 2 所示。
在算法 2 中,我们首先从 X 中随机采样 s 个数据点作为初始 X′(第 1 行)。然后,我们计算覆盖集 Xc ⊂ X,其中每个 x ∈ Xc 被 S x′εX′ B(x′, r) 覆盖。接下来,我们继续使用 k-center-greedy 算法 [Gonzalez, 1985] 将来自 X \ Xc 的新数据点添加到 X′ 中(即选择覆盖范围最大的数据点),直到 S x′∈X′ B(x′, r ) 可以覆盖关于用户定义的阈值 thc 的 X。由于 Hausdorff 距离对异常值的敏感性,特别是当输入数据集包含噪声时,设置阈值 thc < 1。最后,我们可以实现一个与 X 拓扑最相似的最小可能 X′。
半径选择请注意,算法2需要一个预定义的半径,该半径根据Xt在高维空间中的分布进行自适应。直观上,当表示在空间中均匀分布时(例如,在早期训练阶段,X 的 X′ 较大),半径应该很大。相反,当表示在空间中密集聚集时(例如,在训练后期,X 的 X’ 较小),半径可以更小。我们使用公式 3 来计算给定 Xt 分布的半径。
r t = r 0 ( c t c 0 ) α ⋅ ( d t d 0 ) β ( 3 ) r_t=\frac{r_0}{(\frac{c_t}{c_0})^\alpha\cdot(\frac{d_t}{d_0})^\beta}\qquad(3) rt=(c0ct)α⋅(d0dt)βr0(3)
在方程3中,我们首先选择一个参考历元e0,然后计算所有表示c0的最大l2范数作为归一化项,并计算其内在维度[Facco et al., 2017] d0作为表示多样性的度量。然后,我们用公式 3 调整 epoch et 下的半径。这里,r0、α 和 β 是用户定义的阈值。
5 实验
我们通过以下研究问题来评估 TimeVis。更多详情请参见TimeVis 网站[Yang et al., 2022b]
- RQ1:TimeVis 能否忠实反映高维空间中的行进语义?
- RQ2:TimeVis 的可扩展性如何?
- RQ3:虽然TimeVis 具有更强的时间反射性和计算可扩展性,但TimeVis 是否以及如何需要牺牲其他空间属性?
基线、数据集和主题模型 我们选择 DVI 作为基线,因为它是唯一设计用于支持所有空间和时间属性的时间旅行可视化工具。为了进行公平比较,我们在选择数据集和主题模型时遵循DVI的实验设置。具体来说,我们在三个数据集上训练 ResNet18:CIFAR-10、MNIST、Fashion-MNIST。高维表示是从全局平均池层(GAP)中提取的。我们可视化 CIFAR10、MNIST 和 Fashion-MNIST 上分类器的所有训练时期,即 160、20 和 50。
可视化属性测量我们遵循 [Yang et al., 2022c] 中定义的空间和时间测量。具体来说,(1)nnpv(k)用于第k个空间邻居保留测量; (2)boundarypv(k),用于第k个边界邻居保持测量; (3)recpv,用于从低维空间重建表示后的预测保留测量; (4) temppv(k),用于两个连续历元的时间保留测量。
请注意,TimeVis 旨在解决 DVI 所遭受的累积可视化误差,但时间保留测量 temppv(k) 仅评估两个连续历元之间的时间连续性。因此,我们定义了另外两个测量 tempg 和 templ 来评估每个高维表示的移动语义如何跨多个训练时期保留在低维空间中。首先,我们评估在低维空间中可以保留表示 xt i 的多少 k 个最近时间邻居;形式上,我们将 templ(i, t, k) 定义为:
t e m p l ( i , t , k ) = ∑ t ′ = 1 T I ( x i t ′ ∈ N k T ( x i t ) ∧ y i t ′ ∈ N k T ( y i t ) ) k temp_l(i,t,k)=\frac{\sum_{t^{\prime}=1}^T\mathbb{I}(\mathbf{x}_i^{t^{\prime}}\in N_k^T(\mathbf{x}_i^t)\wedge\mathbf{y}_i^{t^{\prime}}\in N_k^T(\mathbf{y}_i^t))}k templ(i,t,k)=k∑t′=1TI(xit′∈NkT(xit)∧yit′∈NkT(yit))
其中 I \mathbb{I} I是评估为 0 或 1 的指示函数。其次,我们评估任何 xt i 的两个排名的相关性。根据距离对其时间邻居进行排名,表示为 r(xt i);另一个按照距离对低维空间中对应的 yt i’ 的时间邻居进行排序,表示为 r(yt i)。然后 tempg 定义为:
t e m p g ( i , t ) = c o r r ( r ( x i t ) , r ( y i t ) ) temp_g(i,t)=corr(r(\mathbf{x}_i^t),r(\mathbf{y}_i^t)) tempg(i,t)=corr(r(xit),r(yit))
我们使用欧几里得距离作为 d(·),使用肯德尔的 τ 作为相关性度量。 tempg(i, t) 越高表示语义保存得越好,反之亦然。
运行时配置 我们让 TimeVis 和 DVI 共享相同的自动编码器架构,即 (r, r 2, r 2, r 2, r 2 , 2) 和 (2, r 2, r 2, r 2, r 2 , r) 给定特征空间维度 r。我们选择 W 作为历元长度。更多配置细节可以参考附录 E [Yang et al., 2022a]。
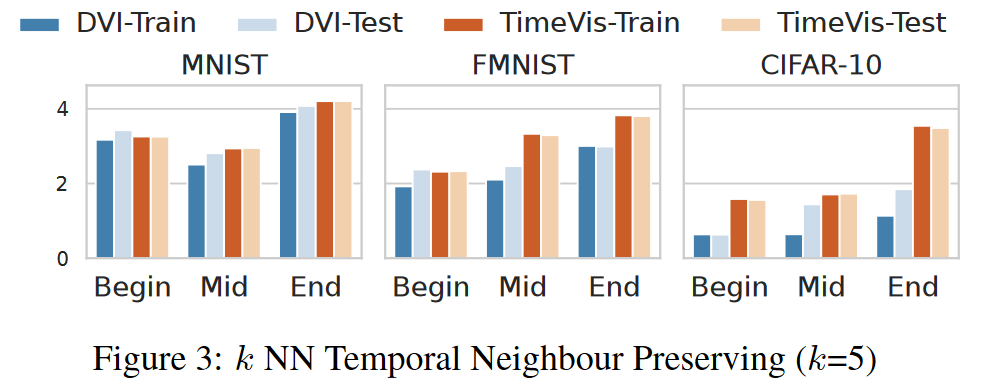
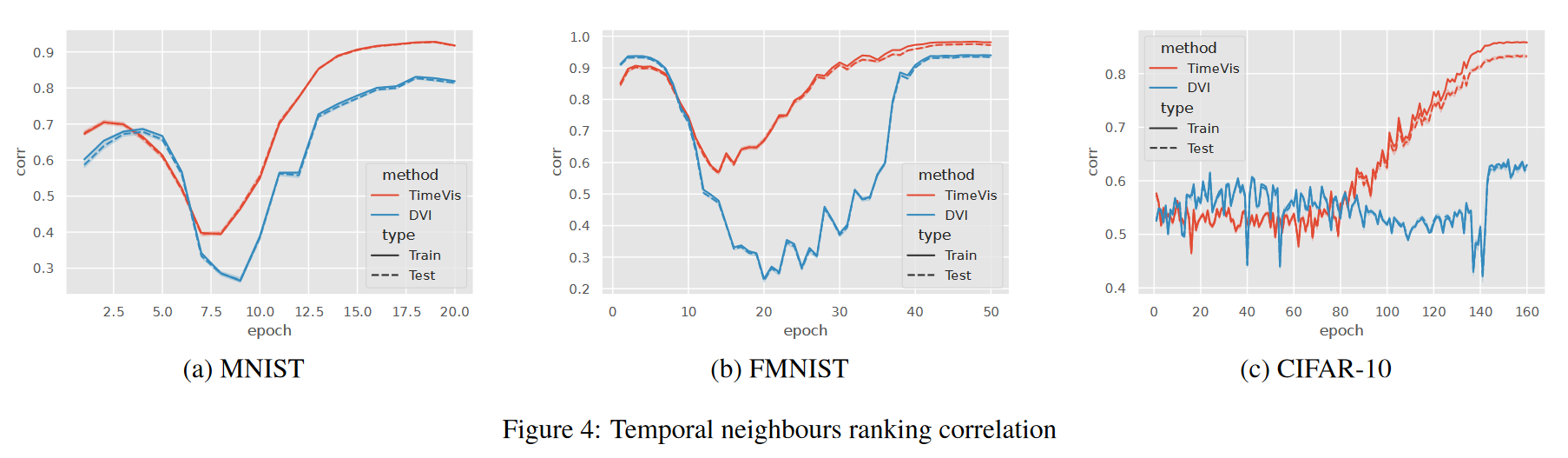
结果(RQ1):保留行进语义 图 3 显示 TimeVis 在不同阶段改进了行进语义。 templ(i, t, k) 的 Mann-Whitney 显着性检验显示 p 值小于 10−5。图 4 进一步显示了两种方法的时间相关性 tempg(i, t) 在训练过程中如何变化。总体而言,TimeVis 优于 DVI,尤其是在后期训练阶段。
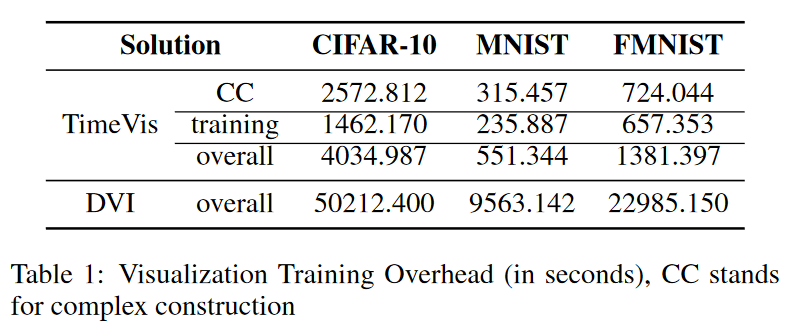
结果 (RQ2):可视化可扩展性 表 1 显示,DVI 的可视化成本是 TimeVis 的 ∼15 倍。与为每个记录的分类器训练可视化模型相比,TimeVis 只需要训练可视化模型一次。
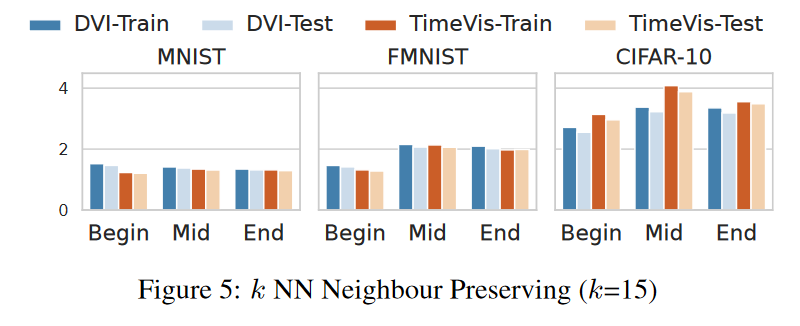
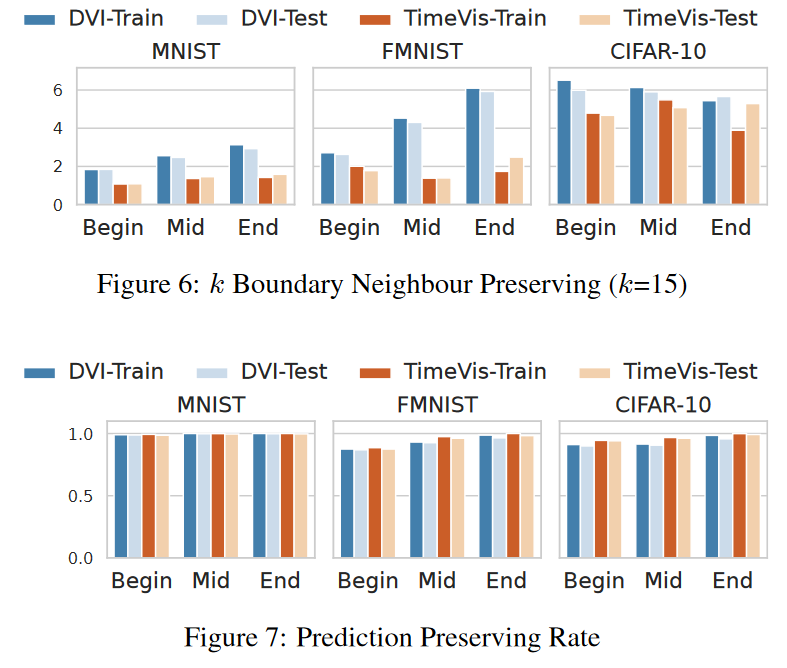
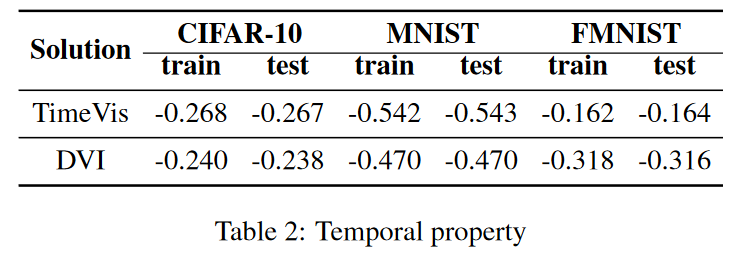
结果 (RQ3):潜在妥协 图 5、图 6、图 7 和表 2 比较了 TimeVis 和 DVI 之间的性能。我们可以看到它们在邻居保留率和预测保留率的测量方面具有可比性。然而,在边界距离保持特性方面,DVI 优于 TimeVis。在未来的工作中,我们将通过改进边界点与时空复合体的整合来增强 TimeVis。
6 相关工作
深度模型的视觉解释 已经提出了许多研究工作来为深度模型提供视觉解释,包括激活图 [Alsallakh et al., 2021; Zeiler 和 Fergus,2014] 和归因方法 [Adebayo 等人,2018]。特别是,IntGrad [Sundararajan et al., 2017] 和 ACE [Chattopadhyay et al., 2019] 是该领域的开创性工作。 TimeVis 专注于可视化训练动态,这是对那些理解深度模型行为的工具的补充。
降维 降维方法广泛用于可视化高维特征向量。现有技术可分为参数化技术(例如,拓扑自动编码器 [Moor et al., 2020]、VAE-SNE [Graving and Couzin, 2020]、参数化 UMAP [Sainburg et al., 2021])和非参数化技术,例如作为 UMAP [McInnes 等人,2018]。
它们是时间旅行可视化的开创性工作。与那些可视化“快照”的技术相比,时间旅行可视化会生成“动画”来理解模型训练过程。
时间旅行可视化 DVI [Yang et al., 2022c] 首先为任何时间旅行可视化方法提出了三个空间和一个时间属性,并训练自动编码器来满足所有属性。然而,DVI仍然存在可视化成本大和可视化误差累积的问题。 TimeVis的提出就是为了解决上述两个问题。
7 结论
我们提出了 TimeVis,一种基于时空化的时间旅行可视化方法。 TimeVis 构建了一个统一的时空复合体,可以捕获任何高维样本的空间和时间邻居。 TimeVis 在训练效率和可视化可靠性方面改进了最先进的解决方案 DVI。未来,将设计基于反馈的解决方案 [Lin et al., 2017]、基于轨迹对齐的解决方案 [Wang et al., 2019] 和基于输入操作的解决方案 [Xiao et al., 2021],以提高工具可用性和可扩展性;
参考文献

-
相关阅读:
Android自定义公共引入库(多个项目引入同一自定义框架类库)
基于STM32+华为云IOT设计的智能衣柜
1488. 避免洪水泛滥
git 提交代码,解决分支冲突,合并分支
01-MQ介绍以及产品比较
一个.NET内置依赖注入的小型强化版
图像和图像处理
linux系统shell脚本开发之循环的使用
【Unity】流体模拟(更新ing)
解决问题:可以用什么方式实现自动化部署
- 原文地址:https://blog.csdn.net/weixin_46112690/article/details/139782766