LeetCode 算法：K 个一组翻转链表 c++

原题链接🔗：K 个一组翻转链表
难度：困难⭐️⭐️⭐️

题目

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例 1：

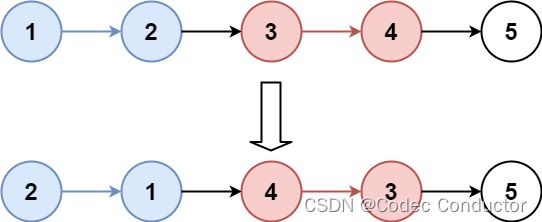
输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

示例 2：

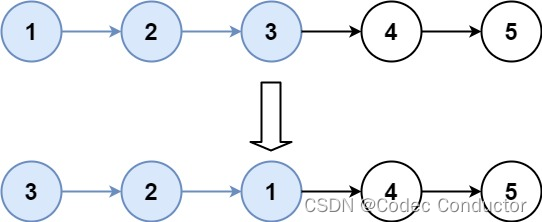
输入：head = [1,2,3,4,5], k = 3
输出：[3,2,1,4,5]

提示：

• 链表中的节点数目为 n
• 1 <= k <= n <= 5000
• 0 <= Node.val <= 1000

进阶：你可以设计一个只用 O(1) 额外内存空间的算法解决此问题吗？

题解

迭代法

1. 题解：

"K 个一组翻转链表"是LeetCode上的一道中等难度的题目，其解题思路可以概括如下：

1. 理解问题：题目要求将给定的链表按照每K个节点为一组进行翻转，如果最后一组不足K个节点，则不翻转。

2. 使用哑节点：在链表的头部添加一个哑节点（dummy node），这样无论原链表的头节点如何变化，哑节点始终作为链表的起始点，简化了边界条件的处理。

3. 遍历链表：从头节点开始遍历链表，找到每K个节点的边界。

4. 翻转每组节点：对于每组找到的K个节点，进行翻转操作。翻转操作可以通过迭代或递归实现。

5. 连接翻转后的节点：将翻转后的节点连接到前一组翻转后的节点后面，形成新的链表。

6. 递归与迭代：递归方法简洁但可能存在栈溢出的风险，迭代方法更安全但代码相对复杂。

7. 边界条件处理：处理链表长度不足K的情况，以及翻转后的链表连接。

下面详细说明迭代方法的步骤：

迭代方法

1. 初始化：使用哑节点指向头节点，定义两个指针groupPrev和curr，分别指向当前组的前一个节点和当前处理的节点。

2. 找到每K个节点：使用curr指针遍历链表，找到每K个节点的最后一位，可以通过一个循环实现。

3. 翻转操作：在找到每K个节点后，使用三个指针（prev、current、next）来翻转这K个节点的连接。

4. 连接翻转后的节点：将翻转后的节点连接到groupPrev后面。

5. 更新指针：更新groupPrev为当前翻转组的最后一个节点，curr为下一个未翻转的节点的开始。

6. 循环：重复步骤2-5，直到curr为nullptr，表示链表已经完全遍历。

7. 返回结果：返回哑节点的下一个节点，即翻转后的链表的头节点。

递归方法

递归方法的核心是将问题分解为更小的子问题：

1. 定义递归函数：递归函数接收当前节点和K值。

2. 终止条件：如果当前节点为空或K为1，直接返回当前节点。

3. 找到K个节点：使用辅助函数找到第K个节点。

4. 翻转操作：翻转当前节点到第K个节点之间的链表。

5. 递归调用：对第K个节点之后的链表进行递归调用。

6. 连接翻转后的节点：将翻转后的子链表连接到翻转前的子链表。

7. 返回结果：返回翻转后的链表。

递归方法的关键在于正确地翻转子链表，并确保递归调用能够正确地处理剩余的链表部分。递归方法的代码实现通常更简洁，但需要注意递归深度和性能问题。

2. 复杂度：时间复杂度O(n)，空间复杂度O(1)。
3. c++ demo：直接应用LeetCode C++10-K个一组翻转链表中的demo。

#include 
#include  //std::shared_ptr
#include  // std::pair

struct Node {
	int value;
	Node* next;
	Node(int value) {
		this->value = value;
		next = nullptr; //这个千万别忘了，否则容易引发segment fault
	}
};

Node* reverse(Node* head) {
	Node* pre = nullptr;
	Node* p = head;
	while (p) {
		auto next = p->next;
		p->next = pre;
		pre = p;
		p = next;
	}
	return pre;
}

// 翻转[head, tail]的元素
std::pair<Node*, Node*> reverse(Node* head, Node* tail) {
	if (head == nullptr || tail == nullptr) {
		return {};
	}
	Node* pre = nullptr;
	Node* p = head;

	// 特别注意：
	// 这里容易错写成while(p != tail->next)，显然是错误的.
	// 原因是tail对应的元素翻转后，tail->next不再指向原来的next，而是指向翻转后的next
	// 除非提前将tail->next在循环外保存，例如：
	// Node* tail_next = tail->next;
	// while (p != tail_next) {...}
	while (pre != tail) { // 这里容易错写成p != tail->next
		Node* next = p->next;
		p->next = pre;
		pre = p;
		p = next;
	}
	return { tail, head };
}

Node* reverse_k(Node* head, int k) {
	std::shared_ptr<Node> dummy_node(new Node(-1));
	dummy_node->next = head;
	Node* pre = dummy_node.get();
	Node* phead = head;
	Node* ptail = pre;//从真正头节点前一个位置出发
	while (phead) {
		for (int i = 0; i < k; i++) {
			ptail = ptail->next;
			if (ptail == nullptr) { //长度不够k则直接返回
				return dummy_node->next;
			}
		}
		Node* next = ptail->next;//先保存tail的下一个位置,防止断链
		auto reverse_ret = reverse(phead, ptail);//翻转[phead, ptail]区间
		phead = reverse_ret.first;
		ptail = reverse_ret.second;
		// 更新连接
		pre->next = phead;
		ptail->next = next;
		// 指针向前移动
		pre = ptail;
		phead = next;
	}
	return dummy_node->next;
}

void print_list(Node* head) {
	Node* p = head;
	while (p) {
		std::cout << p->value << "->";
		p = p->next;
	}
	std::cout << "nullptr" << std::endl;;
}

int main()
{
	// case1: 1->2->3->4->5, k=2 ==> 2->1->4->3->5
	Node n1(1), n2(2), n3(3), n4(4), n5(5);
	n1.next = &n2;
	n2.next = &n3;
	n3.next = &n4;
	n4.next = &n5;
	Node* head = &n1;
	print_list(head);

	head = reverse_k(head, 2);
	std::cout << "case1, k=2:" << std::endl;
	print_list(head);

	// case2: 1->2->3->4->5, k=3 ==> 3->2->1->4->5
	n1.next = &n2;
	n2.next = &n3;
	n3.next = &n4;
	n4.next = &n5;
	head = &n1;
	head = reverse_k(head, 3);
	std::cout << "case2, k=3:" << std::endl;
	print_list(head);

	// case3: 1->2->3->4->5, k=1 ==> 1->2->3->4->5
	n1.next = &n2;
	n2.next = &n3;
	n3.next = &n4;
	n4.next = &n5;
	head = &n1;
	head = reverse_k(head, 1);
	std::cout << "case3, k=1:" << std::endl;
	print_list(head);

	// case4: 1, k = 1 
	n1.next = nullptr;
	head = &n1;
	head = reverse_k(head, 1);
	std::cout << "case3, list is 1->nullptr, k=1:" << std::endl;
	print_list(head);
	return 0;
}

• 输出结果：

1->2->3->4->5->nullptr
case1, k=2:
2->1->4->3->5->nullptr
case2, k=3:
3->2->1->4->5->nullptr
case3, k=1:
1->2->3->4->5->nullptr
case3, list is 1->nullptr, k=1:
1->nullptr